两个绝对值相减求最值_多个绝对值相加求最值问题

今天的内容以绝对值的加法最小值为例，减法也类似，有兴趣的可以自己琢磨一下，此类绝对值的最小值求法被很多老师称之为“奇尖偶平中间最小”，最近遇到一个与此相关的题目，就借此说一下这个问题。

此类问题常见于不等式选讲的绝对值不等式部分，早些年也以函数的形式出现过，现在常见于各高校的自招题目中，以下面两个简单的函数为例：

1.例：y=|x-1|+|x+2|

这种函数求最值可通过分段去掉绝对值符号，作图来求最小值，也可以利用几何意义即点与点之间的距离来求最值，也可利用绝对值三角不等式，在不等式中|a|+|b|≥|a+b|，所以|x-1|+|x+2|=|x-1|+|-2-x|≥|x-1-2-x|=3，若作图，函数的图像为：

此时函数中有两个绝对值组成，且x的系数相同，函数图像为平底，在两个间断点之间取得最小值，若x的系数不同，例如y=|x-1|+|2x+2|,若把x的系数变为1，则可写成三个绝对值形式，即y=|x-1|+|x+1|+|x+1|,此时取得最值的情况和图像就和上述不同了。

2.例:y=|x+1|+|x|+|x-1|

这种情况下x的系数相同，由于是奇数个绝对值，通过绝对值三角不等式很难把右侧转化为常数形式，但如果可以把奇数个绝对值变成偶数个呢？如下：

y=|x+1|+|x|+|x-1|=½[|x+1|+|x+1|+|x|+|x|+|x-1|+|x-1|]≥½|x+1+x+1+x-x+1-x+1-x|=2

可知当绝对值内x系数相同时，无论绝对值为奇数还是偶数均可用绝对值三角不等式来解最小值，作出函数图像，如下：

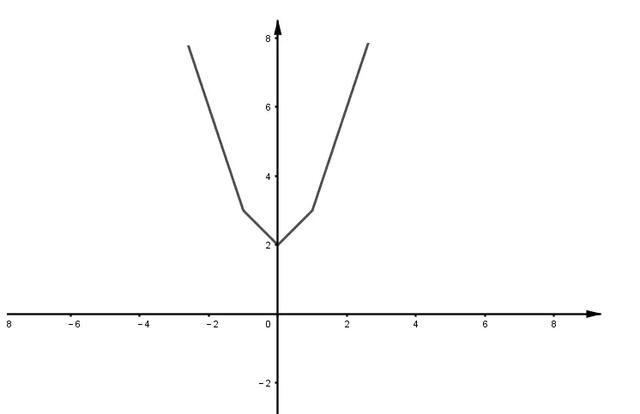
可知函数在x=0处取得最小值，最小值为2，绝对值有奇数个，图像为尖底，这就是所谓的奇尖偶平，至于奇数还是偶数还得看x的系数是否一致，如y=|x-1|+|2x+2|,若将x系数都变为1，则为y=|x-1|+|x+1|+|x+1|,可知函数应为尖底，在x=-1处取得最小值，图像如下：

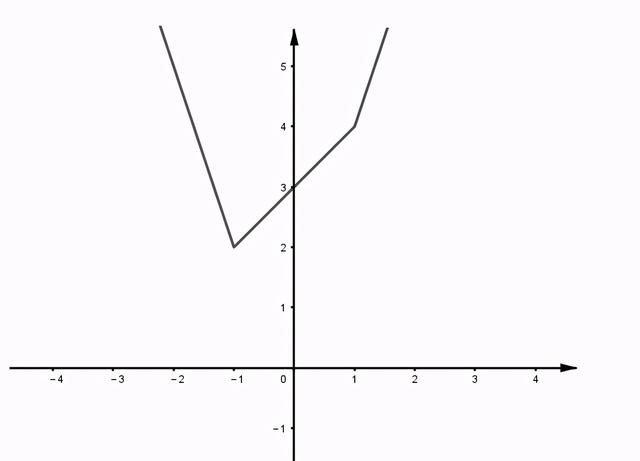
至于“中间最小”，是一种类似于中位数的求最小值所对应的x值方法，统一写成如下形式：

理解这些，在一些与绝对值有关的函数或不等式中的最值就很容易求出来了，下面来看与此相关的高考真题，变式题和自招题：

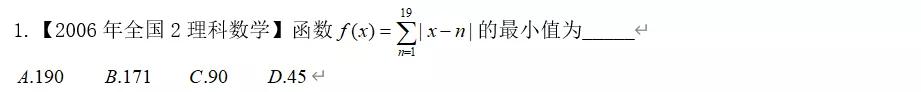
解析：题目为y=|x-1|+|x-2|+...+|x-19|，此时x系数相同，共有19个绝对值，因此当第10个绝对值为零，此时的x值即为取得最小值时的x值，所以当|x-10|=0，即x=10时，取得最小值，最小值为90

解析：利用换元法，令t=x²+2x,则原式变为y=|t-1|+|t-2|+|t-3|，t系数相同，共有三个绝对值，因此当第二个绝对值取得零时，原式取得最小值，即|t-2|=0,t=2,即x²+2x=2，可求出对应的x值，函数的最小值为2

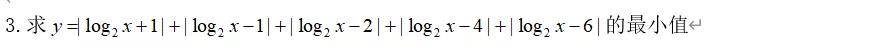
第三题和第二题相同，解决此类问题的关键在于排序，确定x的系数以及绝对值的个数，最后看一个2011年北大的自招题目：

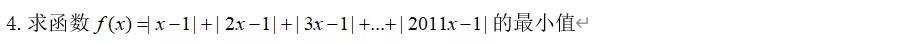
将绝对值中的x系数化为1，如下：

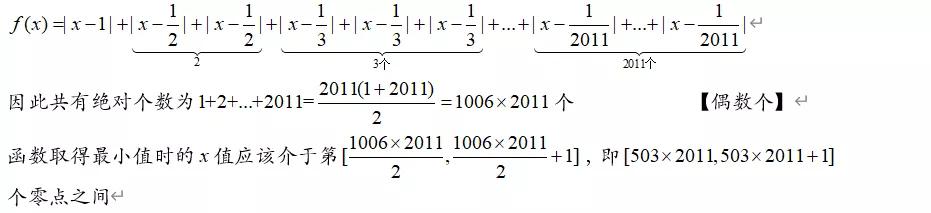
接下来的关键是确定第503×2011项是哪一项，可用等差数列求和不等式来确定

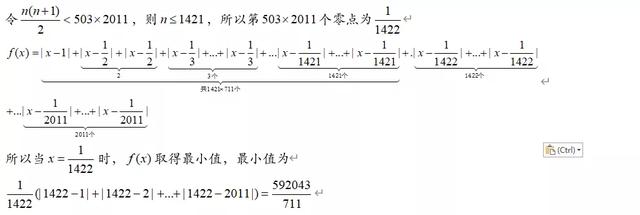
最后用等差求和即可求出最小值，题目结合了绝对值函数最值，不等式，数列求和等知识点，很有意思，如果知道了奇尖偶平中间最小，那么本题目就不算难解。

近期在模考导数题目中看到一类证明多项式之和不等式的问题，明天选出几个题目予以解析，相关题目也可提前看一下链接：求和型导数不等式的证明