伯努利分布方差_最大熵和概率分布

我们需要描述一组数据时候，本质上需要描述每一个点。但是如果我们可以用分布去表示这些数据，就只需要均值或者方差分布参数，大大节省了存储空间。

离散型随机分布

伯努利分布：一次实验，结果只有两种结果。$p(k)=p^k(1-p)^{(1-k)}, kin{0, 1}$，期望：$p$，方差：$p(1-p)$

二项分布：n次伯努利实验正好得到k次成功的概率，单次成功的概率为p。当n=1的时候退化到伯努利分布。当p=0.5的时候，整体上和正态分布图形类似。$p(k)=C_n^kp^k(1-p)^{n-k}$，期望：$np$，方差：$np(1-p)$

几何分布：进行n次伯努利实验，在获取成功前需要进行多少次实验。分布图形是越往前概率越大，$p(k)=(1-p)^{k-1}p$, 期望$frac{1}{p}$, 方差是$frac{(1-p)}{p^k}$

泊松分布：单位时间内独立事件发生次数的概率分布，它是二项分布n很大而p很小时的极限。泊松分布可以把单位时间切成n次，每次成功的概率为p，那么单位时间内出现k次的概率就是二项分布，所以泊松分布是二项分布的一种极限形式。它的分布图形也和二项分布类似，特别是n很大而p很小时。$p(k)=frac{e^{-lambda}lambda^k}{k!}$, 期望和方差都是$lambda$,其中k是发生的次数，$lambda$是发生的平均次数，当$lambda>=20$时，泊松分布趋向于正态分布。

指数分布：对应于泊松分布，指数分布是指两次独立事件发生的时间间隔的概率分布。 $p(k)=lambda e^{-lambda k}$，其中$lambda$是指单位时间内独立事件发生的次数。期望=$frac{1}{lambda}$，方差=$frac{1}{lambda^2}$

负二项分布：在一连串伯努利实验中，恰好在第r+k次实验出现第r次成功的概率。换句话说，是指出现第r次成功时所需要的总实验次数的概率分布。 $p(k,r,p)=C_{r+k-1}^{r-1}p^{r}(1-p)^{k}$，期望$E(k)=frac{k(1-p)}{p}$, 方差$D(k)=frac{k(1-p)}{p^2}$

多项分布：二项分布的扩展。

连续型随机分布

均匀分布：$p(x)=frac{1}{b-a}$，期望$frac{b+a}{2}$， 方差$frac{(b-a)^2}{12}$

正态分布：$p(x)=N(mu, sigma)=frac{1}{sqrt{2pi}sigma}e^{-frac{(x-mu)^2}{2sigma^2}}$，期望$mu$，方差$sigma$。

指数分布：可以扩展到连续随机变量，仍然代表两次独立事件发生的事件间隔（实数）。公式和上面一致。

最大熵

那么以上的概率分布是如何来的呢？最大熵理论提供了一种解释的方法，概率分布是满足一定约束条件下的最大熵概率分布。对于一个随机变量来说，如果没有任何约束，我们大概率倾向于该随机变量符合均匀分布。对应到现实中，如果没有任何前提条件，我们认为事件发生的概率是相同的。比如骰子，我们会默认每一面的概率是1/6。最大熵概率分布满足一下条件：
$$math max_pH(p)=-int_yp(y)logp(y)dy, st. int_yp(y)=1, p(y)>=0, int_yp(y)*f_i(y)dy=a_i $$ 其中ai是预先定好的约束条件，比如均值、方差。 使用拉格朗日乘子得到：

$$math L(p,mu,lambda)=int_yp(y)logp(y)dy - mu_0p(y) + mu_1(int_yp(y)-1) + sum_ilambda_i(int_yp(y)f_i(y)dy-a_i) $$ 其中$mu,lambda$都为正数，解为： $$math p^ = min_p max_{mu,lambda}L=max_{mu,lambda}min_pL $$ 假设y值固定在某个确定的值，对p求偏导： $$math frac{partial L}{partial p} = logp + frac{1}{ln2}-mu_0 + mu_1 + sum_ilambda_if_i(y) = 0 $$ 等式两边乘以ln2，对logp进行换底：

$$math lnp + 1 - mu_0 + mu_1 + sum_ilambda_if_i(y) = 0 $$ 得到解p： $$math p^(y) = e^{ - 1 + mu_0 - mu_1 - sum_ilambda_if_i(y)} = c*e^{-sum_ilambda_if_i(y)} $$

伯努利分布推导

约束条件： $$math f(y) = yrightarrowint_yp(y)y=mu, yin{0,1} $$ 其中$mu$代表事件成功的概率，也是伯努利分布的期望值，得到$ce^{-lambda}=mu$
同时：$p(0) + p(1) = 1 rightarrow c + ce^{-lambda}=1$
由以上两式得到：$c=1-mu, lambda=-lnfrac{mu}{1-mu}$
综合以上：$p(y)=(1-mu)*(frac{mu}{1-mu})^y=(1-mu)^{1-y}mu^y$, 我们就得到了伯努利分布的公式，伯努利分布是在约束期望值下的最大熵概率分布。

正态分布推导

约束条件：均值和方差

其他分布的约束条件

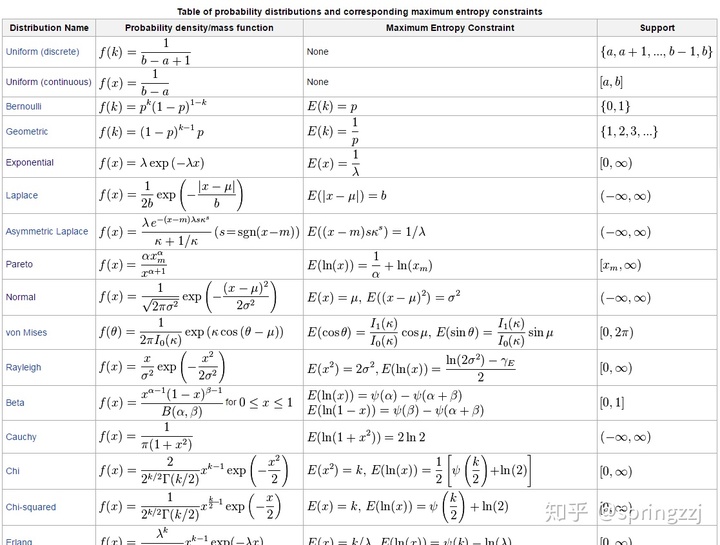
其他概念

概率分布函数，条件概率，联合概率， 独立分布，条件独立，熵， 交 叉熵、条件熵、KL散度