函数最值问题的常用解法_高中数学：无理函数最值问题的常见解法

二次根号下含有自变量的无理函数的最值或值域问题在高中数学竞赛中屡见不鲜，题型丰富多彩解法灵活多变 。

1、换元后转化为二次函数求解

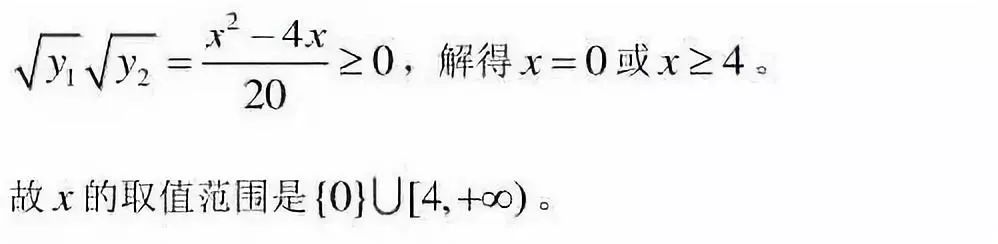
点评：构造一元二次方程，用判别式并结合其它关系求解，但要注意等号能否成立。

4、用y表示x然后利用定义域和不等关系求解

点评：如果能从函数关系式中用y来表示x，则可利用定义域或其它关系列不等式求函数值域。

5、用函数单调性求解

例8(2015年江西省预赛试题)

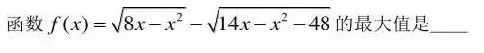
点评：用函数的单调性求函数最值或值域是一种常见方法，本解法是运用单调函数的性质来判断函数的单调性，本题还可用导数来判断函数的单调性，读者可尝试解决。

6、用均值不等式求解

例9(2012年湖北省高中数学竞赛题)

点评：这里二次根号下是一个分式函数，象这样分子分母分别为一次函数和二次函数时，通过换元变形后用均值不等式求解效果较好。

 7、利用柯西不等式求最值

点评：本解法根据式子的轮换对称性通过“不妨设”去掉绝对值，然后用柯西不等式求得最大值。

8、构造几何模型求解

例11(2016年河北省高三年级数学竞赛第5题)求函数

免责声明：文章内容来源于：网络。以上图文，旨在分享，版权归原作者所有。如有侵权，请联系我们立刻删除