离散数学—范式

命题变元或命题变元的否定称为文字。P, ¬P, Q, ¬Q, · · ·

有限个文字的析取称为简单析取式(或子句)。P ∨ Q ∨ ¬R, · · · P,¬P

有限个文字的合取称为简单合取式(或短语)。¬P ∧ Q ∧ R, · · · P,¬P

有限个（大于等于1）简单合取式（短语）的析取式称为析取范式(disjunctive normal form)；

如 (P ∧ Q) ∨ (¬P ∧ Q) 又如 P ∧ ¬Q，P,¬P

有限个（大于等于1）简单析取式（子句）的合取式称为合取范式(conjunctive normal form)。

如 (P ∨ Q) ∧ (¬P ∨ Q)，又如 P ∨ ¬Q，P, ¬P

单独一个的短语（子句），也可以构成析取范式（合取范式）

ps：2中，把P,Q,¬R看作短语，一个短语也可看作析取范式，第3条同理。

1.范式存在定理

对于任意命题公式，都存在与其等价的析取范式和合取范式。

2.范式与真值

命题公式的析取范式可以指出公式何时为真，而合取范式可以指出公式何时为假，从而能够替代真值表。((¬P ∨ Q) ∧ (P ∨ ¬R),¬P ∨ (¬Q ∧ R))

命题公式的范式表达并不唯一，比如对公式 (P ∨ Q) ∧ (P ∨ R) 而言，对应的析取范式有很多：

P ∨ (Q ∧ R)

(P ∧ P) ∨ (Q ∧ R)

P ∨ (Q ∧ ¬Q) ∨ (Q ∧ R)

P ∨ (P ∧ R) ∨ (Q ∧ R)

 一般而言，求解范式时，需要进行最后的化简步骤；

--------------------------------------------------------------------

主范式

1.极小项和极大项

为什么要定义主范式

由于范式的不唯一性，我们考虑对构成范式的子句或短语进一步规范化，从而形成唯一的 主析取范式和主合取范式。

在含有 n 个命题变元 P1, P2, P3, · · · , Pn 的短语或子句中，若每个命题变元与其否定不同时存在， 但二者之一恰好出现一次且仅一次，并且出现的次序与 P1, P2, P3, · · · , Pn 一致，则称此短语或子句为关于 P1, P2, P3, · · · , Pn 的一个极小项或极大项。

 前一个m的下标为P Q的值，后一个下标表示 成真赋值为第i个（从0开始）P Q组合

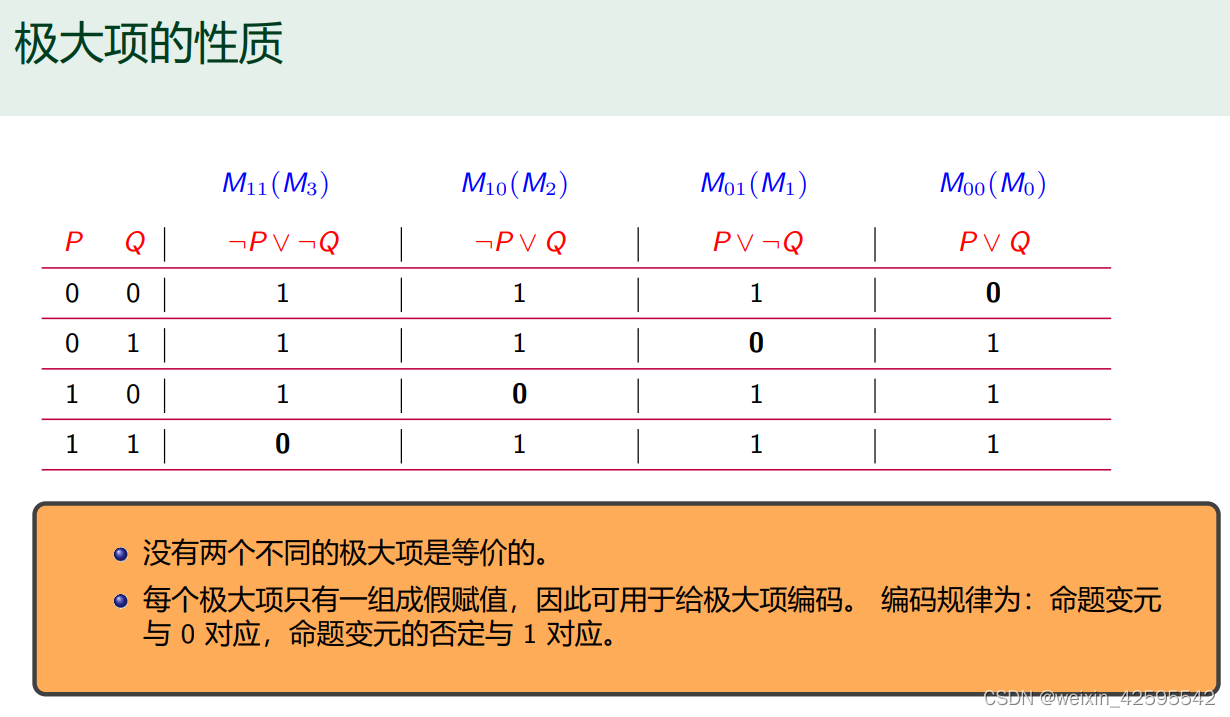
 前一个m的下标表示P Q的值，后一个表示 成假赋值为第i个P Q组合

（后一个m的下标：服从二进制，比如前一个m的下标是110，是6的二进制，则第二个m的下标为6，表示第6个组合，i从0开始）

 2.极小项和极大项的性质

在给定的析取范式中，若每一个短语都是极小项，且按照编码从小到大的顺序排列， 则称该范式为主析取范式(principal disjunctive normal form)。

在给定的合取范式中，若每一个子句都是极大项，且按照编码从小到大的顺序排列， 则称该范式为主合取范式(principal conjunctive normal form)。

如果一个主析取范式不包含任何极小项，则称该主析取范式为 “空”；如果一个主合 取范式不包含任何极大项，则称主合取范式为 “空”。

3.求解方法

第二种方法：真值表技术（略）

4.主析取范式和主合取范式的转化

 由真值表技术可知，对于任一个命题公式而言，主析取范式所使用的极小项的编码和主合 取范式所使用的极大项的编码是 “互补” 的关系。从而我们在求主析取范式和主合取范式 时，可根据公式特点，先求出二者之一，然后可直接写出另一个。

主范式可用于了解公式的真值情况，进行公式类型的判定以及等价关系的判定。

如果主析取范式包含所有的极小项，则该公式为永真公式；

如果主合取范式包含所有的极大项，则该公式为永假公式；

若两个公式具有相同的主析取范式或主合取范式，则两公式等价。 

----------------------------------------------------------------------------------

基本推理形式和蕴涵公式

1.推理的判定定理

公式 H 是前提集合 Γ = {G1, G2, · · · , Gn} 的逻辑结果当且仅当 (G1 ∧ G2 ∧ · · · ∧ Gn) → H 为永真公式。

2.基本蕴涵关系

 ---------------------------------------------------------------------------------

自然演绎法推理

 

1.推理规则

规则 P (称为前提引用规则)：在推导的过程中，可随时引入前提集合中的任意一个前提；

规则 T (称为逻辑结果引用规则)：在推导的过程中，可以随时引入公式 S，该公式 S 是由其 前的一个或多个公式推导出来的逻辑结果。（可以直接使用推导出的中间结果）

规则 CP (称为附加前提规则)：如果能从给定的前提集合 Γ 与公式 P 推导出 S，则能从此前提集合 Γ 推导出 P → S。（结论中的前件，可以当作前提条件来使用）

2.自然演绎法

从前提集合 Γ 推出结论 H 的一个演绎是构造命题公式的一个有限序列： H1, H2, H3, · · · , Hn−1, Hn

其中，Hi 或者是 Γ 中的某个前提，或者是前面的某些 Hj(j < i) 的有效结论，并且 Hn 就是 H， 则称公式 H 为该演绎的有效结论，或者称从前提 Γ 能够演绎出结论 H 来。

具体证明方法（略）