Delphi中的图片处理：二值化和任意角度旋转实践

本文还有配套的精品资源，点击获取

简介：本文深入探讨了Delphi中的图片处理技术，特别是在二值化和任意角度旋转的应用。二值化能够将图像简化为黑白两色，突出边缘细节，常用于图像识别等场景。任意角度旋转则是处理图像时的常见需求，例如在特定项目中用于检测屏幕缺陷。本文指导如何通过Delphi中的Graphics32库和VCL的TBitmap类实现这些功能，并通过创建Delphi项目来具体实践二值化和旋转技术。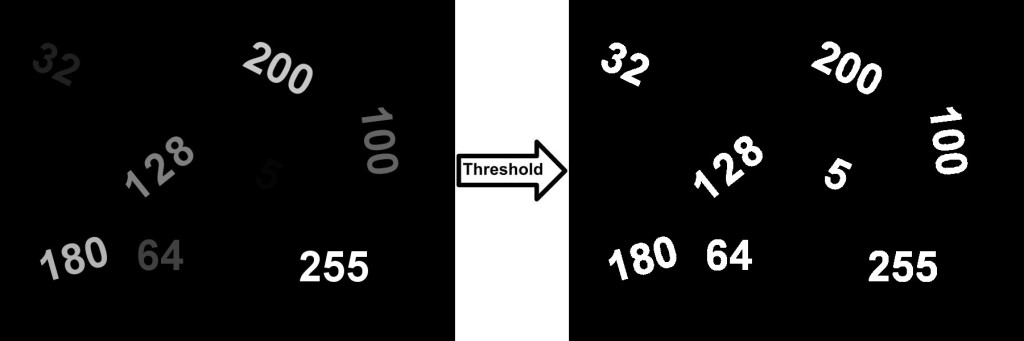

1. Delphi图片处理基础

1.1 Delphi与图像处理简介

Delphi是一种支持快速应用程序开发（RAD）的编程语言，它提供了一系列工具和组件，可以有效地处理图像。对于图像处理领域，Delphi的强大之处在于其丰富的图形库和组件，使得操作图像变得简单快捷。从加载、显示到图像的转换、处理和保存，Delphi通过直观的编程接口简化了复杂的过程。

1.2 图像处理的重要性

在信息技术飞速发展的今天，图像处理已经成为不可或缺的一部分。无论是医疗成像、卫星图像分析、还是日常的文档处理，图像处理技术都被广泛应用。Delphi凭借其简洁的语法和强大的功能，为开发者提供了一个高效的平台，进行图像处理相关的工作。

1.3 Delphi图像处理的基本操作

Delphi提供的TBitmap类是图像处理的基础。通过这个类，可以实现图像的加载、保存、格式转换等多种功能。此外，Delphi还支持第三方图形库如Graphics32，这为Delphi进行图像处理提供了更多高级功能和算法支持。在实际开发过程中，理解并运用这些基础操作是进行更复杂图像处理任务的前提。

// 示例代码：TBitmap类加载图像
var
  Bitmap: TBitmap;
begin
  Bitmap := TBitmap.Create;
  try
    Bitmap.LoadFromFile('path_to_image.jpg'); // 加载图像文件
    // 在此处可以对Bitmap进行进一步处理
  finally
    Bitmap.Free;
  end;
end;

本章节介绍了Delphi在图像处理领域的基础作用，以及如何在Delphi环境下进行简单的图像加载操作。后续章节将深入探讨更多高级图像处理技术。

2. 二值化技术及其应用

2.1 二值化技术的理论基础

2.1.1 二值化概念及其重要性

在图像处理中，二值化是一种将图像转换为黑白两色的技术，其中每个像素点的值仅由0（黑色）和255（白色）构成。这种技术对于提高图像的对比度、简化图像内容以及为后续处理如文本识别和边缘检测等提供便利十分关键。二值化技术在文档图像处理、医学影像分析和机器视觉等领域有广泛应用。

2.1.2 二值化技术的原理和分类

二值化算法的核心在于确定一个阈值。对于每个像素点，如果其灰度值大于该阈值，就将其设置为白色；如果小于或等于该阈值，则设为黑色。这种技术根据阈值的确定方式，可以分为全局阈值和局部阈值二值化。全局阈值在整个图像中是固定的，适合于光照均匀、对比度高的图像；局部阈值则随着图像的不同区域而变化，适合处理光照不均和复杂背景的图像。

2.2 二值化技术的实现方法

2.2.1 Delphi中实现二值化的步骤

在Delphi中实现二值化，可以借助内置的图像处理库，如VCL或FireMonkey框架中的TBitmap类，也可以使用第三方库如Graphics32。以下是使用TBitmap进行二值化处理的基本步骤：

1. 加载图像到TBitmap对象中。
2. 遍历图像中的每一个像素。
3. 对每个像素的灰度值进行比较，根据阈值判断并赋予新的值。
4. 更新图像的每个像素值，形成二值化后的图像。
5. 显示或保存处理后的图像。

下面是使用Delphi中的代码示例：

procedure BinaryImage(srcBitmap, destBitmap: TBitmap);
var
  x, y: Integer;
  threshold: Byte;
  pixel: TColor;
begin
  // 假定阈值已根据需要设定
  threshold := 128;
  destBitmap.SetSize(srcBitmap.Width, srcBitmap.Height);
  for x := 0 to srcBitmap.Width - 1 do
    for y := 0 to srcBitmap.Height - 1 do
    begin
      pixel := srcBitmap.Canvas.Pixels[x, y];
      // 使用阈值进行二值化
      if GetIntensity(pixel) > threshold then
        destBitmap.Canvas.Pixels[x, y] := clWhite
      else
        destBitmap.Canvas.Pixels[x, y] := clBlack;
    end;
end;

GetIntensity 是一个自定义函数，用于从彩色图像中提取灰度值。上述代码展示了基本的二值化处理流程，其中对每像素的灰度值和阈值进行比较，根据比较结果更新为黑色或白色。

2.2.2 二值化参数调整与优化

二值化处理效果受到阈值参数的直接影响。选择合适的阈值对于不同应用场景至关重要。常见的方法包括使用Otsu方法自适应计算最佳阈值。在Delphi中可以这样实现：

procedure CalculateOtsuThreshold(srcBitmap: TBitmap; var threshold: Byte);
var
  histogram: array[0..255] of Integer;
  totalPixels, sum, weight1, weight2, maxVar: Integer;
  i, j: Integer;
  level: Byte;
begin
  // 初始化直方图
  FillChar(histogram, SizeOf(histogram), 0);
  totalPixels := srcBitmap.Width * srcBitmap.Height;
  for i := 0 to srcBitmap.Height - 1 do
    for j := 0 to srcBitmap.Width - 1 do
    begin
      level := GetIntensity(srcBitmap.Canvas.Pixels[j, i]);
      Inc(histogram[level]);
    end;

  sum := 0;
  for i := 0 to 255 do
  begin
    sum := sum + i * histogram[i];
    weight1 := 0;
    for j := 0 to i - 1 do
      weight1 := weight1 + histogram[j];
    weight2 := totalPixels - weight1;
    if weight1 = 0 then continue;
    if weight2 = 0 then break;
    maxVar := sum * weight1 * weight2 - totalPixels * power(weight1, 2);
    if maxVar > 0 then
    begin
      threshold := i;
      Break;
    end;
  end;
end;

该函数通过计算图像灰度直方图，使用Otsu算法自动计算出最佳阈值。这个过程有利于自动化处理，并减少人工干预。

2.3 二值化在实际应用中的案例分析

2.3.1 文档图像的二值化处理

文档图像处理通常需要清晰地展示文字内容，因此二值化处理在此类应用中非常有用。例如，在OCR（Optical Character Recognition）应用中，清晰的二值化图像可以提高文字识别的准确性。在Delphi中，可以通过上述步骤和优化方法来处理扫描得到的文档图像，并将其转换为适用于OCR的二值化图像。

2.3.2 手写识别与二维码识别中的二值化

手写识别和二维码识别都要求图像具有高的对比度和清晰的边缘。在这种情况下，二值化技术显得尤为重要。通过调整阈值来优化二值化过程，可以提升识别率。

对于手写识别，图像预处理阶段的二值化可以减少背景噪声，突出手写笔迹，使后续的笔迹跟踪和特征提取更加准确。

在二维码识别中，二值化可以帮助突出二维码区域，去除多余的背景干扰，从而提高识别算法的准确性和效率。

在上述案例中，二值化技术的应用不仅可以单独作为一种处理步骤，也可以和其他图像处理技术（如图像滤波、边缘检测等）结合使用，以达到更好的处理效果。

3. 任意角度图像旋转技术

在现代图像处理中，旋转技术是基础而又关键的功能之一。无论是进行图像预处理还是图像增强，正确地旋转图像均能发挥着举足轻重的作用。本章将详细探讨图像旋转的技术基础，Delphi环境下实现任意角度图像旋转的方法，并分析旋转技术在图像处理中的实际应用。

3.1 图像旋转技术的理论基础

3.1.1 旋转的基本概念与数学模型

图像旋转是指将图像按照给定的角度进行空间变换，使图像中的对象按照一定的角度进行偏转。在二维图像处理中，旋转通常围绕一个中心点进行。从数学模型的角度来看，图像中的每一点在旋转过程中都将遵循一定的几何变换规则，通常是线性变换。基本的二维旋转矩阵如下：

[ cos(θ) -sin(θ) ]
[ sin(θ)  cos(θ) ]

其中， θ 是旋转的角度。如果图像需要围绕一个特定的点（不在图像中心）进行旋转，则需要先平移图像，使得旋转中心位于原点，进行旋转后再进行平移恢复到原来的位置。

3.1.2 旋转角度的确定方法

旋转角度的确定方法取决于旋转的目的。在某些情况下，旋转角度由用户直接指定，例如，在UI设计中，用户可能需要将图像旋转一个特定的角度以达到设计效果。而在其他一些应用场景中，如文档图像预处理，旋转角度可能需要通过图像处理算法来自动计算。例如，检测图像边缘并确定图像的倾斜程度，然后根据倾斜程度计算出需要旋转的角度来纠正图像。

3.2 Delphi实现图像任意角度旋转的方法

3.2.1 利用Graphics32库进行旋转

在Delphi中实现图像旋转，可以使用现有的库，如Graphics32。Graphics32是一个功能强大的第三方图形处理库，它提供了丰富的图像处理功能，包括图像旋转。下面是使用Graphics32库进行图像旋转的基本步骤：

uses
  Graphics, GR32;

procedure RotateImage(FileName, OutputFileName: string; const Angle: Double);
var
  Bitmap: TBitmap32;
  Bitmap32Format: TBitmap32Format;
begin
  Bitmap := TBitmap32.Create;
  try
    Bitmap32Format := TBitmap32Format العسك32;
    Bitmap.LoadFromFile(FileName, Bitmap32Format);
    Bitmap.Rotate(0, 0, Angle);
    Bitmap.SaveToFile(OutputFileName, Bitmap32Format);
  finally
    Bitmap.Free;
  end;
end;

上述代码中， Rotate 方法接受旋转中心（本例中为图像中心，即坐标(0,0)）和旋转角度（以弧度为单位）。需要注意的是， Graphics32库的旋转函数在内部已经处理了平移和恢复的过程。

3.2.2 自定义函数实现精确旋转

除了使用第三方库，我们也可以自定义函数来实现图像的任意角度旋转。自定义旋转函数涉及线性代数中的矩阵运算，通过设置旋转矩阵来实现。以下是一个自定义的旋转函数示例：

uses
  GR32, GR32_Image, GR32_Transforms;

procedure CustomRotateImage(Bitmap: TBitmap32; Angle: Double);
var
  M: TAffineMatrix;
begin
  M := AffineMatrixTranslation(-Bitmap.Width / 2, -Bitmap.Height / 2);
  M := M * AffineMatrixRotation(Angle);
  M := M * AffineMatrixTranslation(Bitmap.Width / 2, Bitmap.Height / 2);
  Bitmap.SetSize(Bitmap.Width, Bitmap.Height);
  Bitmap.Transform(M);
end;

在这里，首先将图像中心移动到原点，然后应用旋转矩阵，最后将图像中心移回原来的位置。这样便完成了自定义的图像旋转操作。

3.3 旋转技术在图像处理中的应用

3.3.1 图像预处理中的旋转应用

在图像预处理阶段，图像旋转技术用于纠正倾斜或调整图像的方向。例如，在文档图像处理中，文档可能因为扫描时的偏差导致图像倾斜。通过计算倾斜角度并应用逆向旋转，可以将文档图像校正为标准位置，这对后续的文本识别过程至关重要。

3.3.2 图像增强与复原中的旋转策略

图像增强与复原是图像处理的重要方面，旋转技术在此环节中也有其独特的作用。例如，在数字摄影中，为了校正由于拍摄角度导致的透视失真，可以使用旋转技术对图像进行调整。另外，在图像复原过程中，有时需要将图像旋转到特定角度，以便使用其他图像处理技术进行更好地修复或增强。

总结来说，任意角度图像旋转技术是图像处理中的关键技术和基础，它为图像预处理、增强和复原提供了强大的支持。通过理解旋转技术的理论基础，我们可以更好地在实际应用中，比如使用Delphi这样的编程语言，来实现精确和高效的图像旋转操作。在后续章节中，我们将进一步探讨图形处理库的使用以及坐标系统转换在图像处理中的应用，为图像旋转提供更深入的技术支持。

4. Graphics32库与TBitmap类的使用

4.1 Graphics32库的介绍与安装

4.1.1 Graphics32库的特点与优势

Graphics32是一个高性能的图像处理库，专门为Delphi语言开发。它是开源的，因此您可以免费使用，并可以查看源代码以改进和适应您的项目需求。Graphics32的主要特点包括：

• 支持32位彩色图像 ，每个像素使用4个字节表示，这是Windows系统中常见的图像格式。
• 快速的图形操作 ，利用指针和像素块操作，大大提高了图像处理的速度。
• 完善的图像处理功能 ，包括颜色转换、图像变换、滤镜效果等。
• 良好的兼容性 ，可以与Delphi的VCL框架无缝集成，适用于多种版本的Delphi。

它的优势在于提供了一个直观且功能强大的API，使得开发者能够轻松地实现图像的加载、保存、显示和各种图像处理功能。

4.1.2 Graphics32库的安装与配置

安装Graphics32库的步骤相对简单，可以通过以下步骤完成：

1. 下载Graphics32 ：首先，需要从官方网站或GitHub上获取Graphics32库的最新版本。
2. 解压到指定目录 ：解压下载的文件到您选择的目录中。
3. 编译和安装 ：打开Delphi IDE，然后导入 Graphics32.dpk （或相应的Delphi包文件），编译并安装到IDE中。

完成以上步骤后，就可以在Delphi项目中使用Graphics32库了。您可以将它添加到您的项目文件中，或者直接从组件面板拖动相应的组件到窗体中。

4.2 TBitmap类的基本操作

4.2.1 TBitmap类的主要属性和方法

TBitmap是Delphi中用于图像处理的一个核心类，它提供了丰富的属性和方法来操作位图图像。TBitmap类的主要属性和方法包括：

• 像素操作 ：通过 Canvas.Pixels 和 Canvas.ScanLine 可以访问和修改图像中的单个像素。
• 图像加载与保存 ： LoadFromFile 和 SaveToFile 方法用于加载和保存图像到文件。
• 图像类型转换 ：可以使用 Monochrome 、 Grayscale 等方法将彩色图像转换为灰度或黑白图像。
• 图像缩放与旋转 ： StretchDraw 方法可以对图像进行缩放，而旋转功能则可以通过其他库函数或自定义算法实现。

4.2.2 位图加载、创建与显示技巧

要加载一张位图，可以使用以下代码示例：

var
  MyBitmap: TBitmap;
begin
  MyBitmap := TBitmap.Create;
  try
    MyBitmap.LoadFromFile('path_to_image_file');
    // 在此处可以对MyBitmap进行操作
  finally
    MyBitmap.Free;
  end;
end;

创建一个空白位图的代码如下：

var
  MyBitmap: TBitmap;
begin
  MyBitmap := TBitmap.Create;
  try
    // 可以指定宽度和高度创建空白位图
    MyBitmap.Width := 100;
    MyBitmap.Height := 100;
    // 在此处可以对MyBitmap进行操作
  finally
    MyBitmap.Free;
  end;
end;

为了显示位图，您可以使用 TImage 组件，并将TBitmap对象赋值给 Picture 属性，如：

procedure TForm1.ButtonLoadClick(Sender: TObject);
var
  MyBitmap: TBitmap;
begin
  MyBitmap := TBitmap.Create;
  try
    MyBitmap.LoadFromFile('path_to_image_file');
    Image1.Picture.Bitmap := MyBitmap;
  finally
    MyBitmap.Free;
  end;
end;

位图的显示还可以在VCL表单上直接绘制，使用 Canvas 对象画图，代码示例如下：

procedure TForm1.FormPaint(Sender: TObject);
var
  MyBitmap: TBitmap;
begin
  MyBitmap := TBitmap.Create;
  try
    MyBitmap.LoadFromFile('path_to_image_file');
    Canvas.Draw(0, 0, MyBitmap);
  finally
    MyBitmap.Free;
  end;
end;

4.3 Graphics32库的高级图像处理功能

4.3.1 高级图形绘制与效果实现

Graphics32库不仅提供了基本的图像处理功能，还允许开发者实现一些高级的图形绘制和视觉效果。这些功能包括：

• 透明度处理 ：通过调整像素的Alpha通道值实现图像的半透明效果。
• 颜色混合与调整 ：使用颜色混合函数可以轻松创建多种颜色效果。
• 图像滤镜 ：支持多种图像滤镜，例如模糊、锐化、高斯模糊等。

以下是一个简单的示例代码，展示了如何使用Graphics32实现图像的模糊效果：

uses
  GR32, GR32_FILTERS;

procedure TMainForm.ApplyBlurEffect;
var
  MyBitmap: TBitmap32;
begin
  MyBitmap := TBitmap32.Create;
  try
    MyBitmap.SetSize(Image1.Width, Image1.Height);
    MyBitmap.Draw(0, 0, Image1.Picture.Bitmap);
    // 应用模糊滤镜
    BoxBlur(MyBitmap, MyBitmap.BoundsRect, 5);
    Image1.Picture.Bitmap.Assign(MyBitmap);
  finally
    MyBitmap.Free;
  end;
end;

4.3.2 图像滤镜与特殊效果处理

在图像处理中，滤镜效果是非常重要的一部分，它们可以改变图像的外观，创造出不同的艺术风格或提高视觉上的可读性。在Graphics32中，可以使用内置的滤镜类来实现多种视觉效果。

例如，要使用高斯模糊滤镜，可以使用以下代码：

uses
  GR32, GR32_FILTERS;

procedure TMainForm.ApplyGaussianBlurEffect;
var
  MyBitmap: TBitmap32;
  Filter: TCustomFilter;
begin
  MyBitmap := TBitmap32.Create;
  try
    MyBitmap.SetSize(Image1.Width, Image1.Height);
    MyBitmap.Draw(0, 0, Image1.Picture.Bitmap);
    // 初始化高斯模糊滤镜
    Filter := TGaussianBlurFilter.Create;
    try
      Filter.BlurRadius := 5;
      Filter.Execute(MyBitmap);
    finally
      Filter.Free;
    end;
    Image1.Picture.Bitmap.Assign(MyBitmap);
  finally
    MyBitmap.Free;
  end;
end;

这些滤镜类可以在图像上施加各种效果，包括模糊、锐化、边缘检测等。通过这些高级功能，开发者可以为应用程序或项目添加独特的图像处理能力。

以上内容仅为Graphics32库和TBitmap类使用的基础介绍。随着读者对这些内容的理解，可以进一步探索库中的其他高级特性，并根据个人需求开发出创新的图像处理功能。

5. 图像处理中极坐标与直角坐标的转换

5.1 极坐标与直角坐标的数学基础

5.1.1 极坐标与直角坐标的定义

极坐标系统提供了一种描述平面上点位置的方法，与直角坐标系统不同，极坐标使用一个角度和一个距离来定位点，而非传统的x和y轴。在极坐标系统中，每个点由一对数 (r,θ) 表示，其中 r 是点到原点的距离，θ 是从正x轴到点的向量与x轴之间的角度。直角坐标系统则使用一对数 (x,y) 来表示点的位置，其中x代表水平位置，y代表垂直位置。

5.1.2 坐标转换的数学原理

极坐标转换为直角坐标的关键在于理解转换方程式： - x = r * cos(θ) - y = r * sin(θ)

反之，直角坐标转换为极坐标需要确定点到原点的距离 r 和角度 θ，通过以下方程式实现： - r = √(x² + y²) - θ = arctan(y/x)，注意要处理当x为负时，θ的计算需要加上π或180度。

5.2 Delphi中的坐标转换实现

5.2.1 Delphi中的坐标转换函数

在Delphi中，可以使用Math单元提供的三角函数来实现坐标转换。首先，需要确保已经引入Math库。

uses
  Math;

接下来，定义一个函数，将极坐标转换为直角坐标：

function PolarToCartesian(r, theta: Extended): TPoint;
begin
  Result.X := r * Cos(theta * Pi / 180);
  Result.Y := r * Sin(theta * Pi / 180);
end;

反之，可以定义另一个函数，将直角坐标转换为极坐标：

function CartesianToPolar(x, y: Extended): TPolarCoord;
var
  r: Extended;
begin
  r := Sqrt(x * x + y * y);
  if x > 0 then
    Result.Theta := ArcTan(y / x) * 180 / Pi
  else if x < 0 then
    Result.Theta := ArcTan(y / x) * 180 / Pi + 180
  else if y > 0 then
    Result.Theta := 90
  else if y < 0 then
    Result.Theta := -90
  else
    Result.Theta := 0;
  Result.R := r;
end;

5.2.2 应用坐标转换进行图像处理

在图像处理任务中，坐标转换可以用于图像分析、特征提取、图像变形等操作。例如，假设我们有一个图像，需要将其中的一个图案旋转到指定角度。我们可以通过坐标转换来计算旋转后图案的新坐标。

var
  image: TBitmap;
  i, j, newCenterX, newCenterY: Integer;
  center: TPoint;
  angle, rad: Extended;
begin
  image := TBitmap.Create;
  try
    // Load the image
    image.LoadFromFile('path_to_image');
    center := Point(image.Width div 2, image.Height div 2);
    angle := 45; // Assume we want to rotate the image by 45 degrees.
    rad := angle * Pi / 180;

    // Iterate through each pixel of the image and apply rotation
    for i := 0 to image.Width - 1 do
      for j := 0 to image.Height - 1 do
      begin
        // Convert Cartesian coordinates to polar relative to center
        newCenterX := i - center.X;
        newCenterY := j - center.Y;
        with PolarToCartesian(1, rad) do
        begin
          // Apply transformation
          newCenterX := Round(newCenterX + center.X);
          newCenterY := Round(newCenterY + center.Y);
        end;

        // If the new pixel is within the image bounds, copy the color
        if (newCenterX >= 0) and (newCenterX < image.Width) and
           (newCenterY >= 0) and (newCenterY < image.Height) then
          image.Canvas.Pixels[newCenterX, newCenterY] := image.Canvas.Pixels[i, j];
      end;
  finally
    image.Free;
  end;
end;

5.3 坐标转换在图像处理中的应用

5.3.1 图像分析与特征提取中的应用

在图像分析和特征提取中，坐标转换常常用于处理图像中的几何特性。例如，通过极坐标转换，可以更容易地识别和测量图像中的圆形结构，因为圆在极坐标中是一条直线。

5.3.2 图像校正与变形处理中的应用

在图像校正和变形处理中，坐标转换用于实现图像的旋转、缩放和平移等变换。通过数学模型，可以精确地计算出图像变形后每个像素的新位置，从而达到预期的图像校正效果。

接下来的章节将探讨矩阵变换在图像旋转中的应用，并深入到实际的项目案例分析中去。

6. 矩阵变换在图像旋转中的应用

6.1 矩阵变换的理论基础

矩阵变换是现代图像处理中不可或缺的一部分，特别是在图像旋转的场合。在这一小节中，我们将深入了解矩阵变换的基础知识及其在图像处理领域的应用。

6.1.1 线性代数中的矩阵变换概念

矩阵变换是线性代数中的一种变换方式，它能够将一个向量空间中的点映射到另一个点。具体到二维图像上，这意味着我们可以使用矩阵来表示并实现图像的缩放、旋转、倾斜、平移等操作。每一个变换都对应一个特定的变换矩阵，例如旋转矩阵、平移矩阵等。

在图像处理领域，矩阵变换尤其重要，因为它们可以高效地描述和实现复杂的几何操作。例如，一个旋转操作可以用一个旋转矩阵来表达，而图像的每一个像素点都可以通过这个矩阵来得到新的位置。

6.1.2 矩阵变换在图像处理中的角色

在图像处理过程中，矩阵变换不仅能够实现基本的几何操作，还能够在不改变图像结构的前提下优化图像内容。使用矩阵变换进行旋转，可以在保持图像内容不变的同时，调整图像的方向。

此外，矩阵变换也经常用于图像配准、图像融合以及模式识别等高级图像处理技术中。在图像配准中，通过矩阵变换可以将不同视角或不同时间拍摄的图像对齐到同一坐标系中；在图像融合中，矩阵变换能帮助整合多张图像信息；在模式识别中，矩阵变换常被用于特征提取和数据降维。

6.2 Delphi实现矩阵变换的方法

6.2.1 Delphi中的矩阵操作类介绍

在Delphi中，我们可以借助第三方库如Mathematics、Graphics32等来实现矩阵操作。Delphi本身提供了一些基本的矩阵操作方法，但对图像处理而言，这些方法有时不够高效和专业。

借助第三方库，我们可以更加方便地操作矩阵，比如创建矩阵、进行矩阵乘法、求逆矩阵等。例如，在Graphics32库中，我们可以使用 TMatrix 类来处理图像的矩阵变换。

6.2.2 构建旋转矩阵与变换实践

旋转矩阵的构建基于三角函数，用于实现图像的旋转。例如，一个逆时针旋转θ角度的2D旋转矩阵可以表示为：

| cosθ   -sinθ |
| sinθ    cosθ |

在Delphi中，我们可以通过以下代码示例来构建一个旋转矩阵并应用于图像旋转：

uses
  GR32, GR32_Math;

procedure RotateImage(Bitmap: TBitmap32; Angle: Single);
var
  M: TMatrix32;
begin
  // 初始化旋转矩阵
  M := TMatrix32.Affine(
    [
      Cos(Angle), -Sin(Angle),
      Sin(Angle),  Cos(Angle),
      0, 0
    ]
  );
  // 应用旋转矩阵到图像
  Bitmap.Transform(M);
end;

此代码段创建了一个旋转矩阵 M ，然后将该矩阵应用于图像 Bitmap ，从而实现图像的旋转。

6.3 矩阵变换在图像旋转中的优化策略

6.3.1 提高旋转效率的矩阵优化技术

矩阵变换在图像旋转中的效率优化是一个重要的议题。为了提高效率，可以使用一系列优化技术，如分块处理、预计算旋转矩阵、使用查找表（LUTs）等。

分块处理是将图像划分成小块，然后分别对每个块进行矩阵变换，最后将变换后的块拼接起来。这样可以减少内存访问次数，提高旋转效率。预计算旋转矩阵则是事先计算出旋转矩阵，避免在实时旋转操作中重复计算矩阵。查找表是将可能的矩阵值事先计算好，并存储起来，旋转时直接查询使用，这样可以显著加快矩阵乘法的速度。

6.3.2 防止图像失真的旋转算法

图像在旋转过程中容易出现失真，这通常是由于插值算法不准确导致像素错位。为了防止图像失真，可以采取多种措施，比如使用双线性插值、双三次插值等插值算法。

在Delphi的 TBitmap32 类中，可以指定插值方法来保证旋转后图像的清晰度。例如，使用 Bitmap.DrawTo(ACanvas, DestRect, SrcRect, True, 8); 时， 8 表示使用8位深度进行插值，这有利于保证图像质量。

此外，还可以采用边界扩展、镜像和环绕等策略来处理图像边缘像素，这些措施都可以减少旋转过程中可能发生的图像失真现象。

为了使本章节内容更加丰富和深入，下面通过一个代码块和一个表格来展示矩阵变换中的常用技术。

代码块：应用查找表优化旋转矩阵计算

// 使用查找表优化旋转矩阵
var
  SinTable, CosTable: array of Single;
  I: Integer;
begin
  // 初始化查找表
  SetLength(SinTable, 360);
  SetLength(CosTable, 360);
  for I := 0 to 359 do
  begin
    SinTable[I] := Sin(DegToRad(I));
    CosTable[I] := Cos(DegToRad(I));
  end;

  // 使用查找表计算旋转矩阵
  procedure GetCosSinForAngle(Angle: Integer; out CosSin: TAffineVector);
  var
    Index: Integer;
  begin
    Index := Angle mod 360;
    CosSin.X := CosTable[Index];
    CosSin.Y := SinTable[Index];
    CosSin.Z := 0;
  end;
end;

在这个代码块中，我们首先初始化了正弦和余弦值的查找表，然后创建了一个函数 GetCosSinForAngle 来快速获得角度对应的旋转矩阵。这种方法可以避免在旋转图像时重复计算正弦和余弦值，从而提升效率。

表格：旋转算法的比较

| 旋转算法 | 优点 | 缺点 | |-----------|--------------------------|----------------------------| | 基本旋转变换 | 简单易实现，适用于实时处理 | 可能产生像素空洞，导致图像质量下降 | | 双线性插值 | 图像质量较好，适合于多种图像 | 运算量较大，效率相对较低 | | 双三次插值 | 图像质量更加细腻，适合高质量图像 | 运算量大，效率低，需更高硬件支持 |

以上就是第六章“矩阵变换在图像旋转中的应用”的全部内容。通过本章节的学习，我们不仅了解了矩阵变换在图像旋转中的基本理论，还掌握了在Delphi环境下实现图像旋转的具体方法。此外，我们还学习到了优化矩阵变换的策略以及如何避免旋转过程中的图像失真，这些都对实际开发具有指导意义。

7. 图像旋转的填充和裁剪处理

7.1 图像填充与裁剪的理论介绍

7.1.1 填充与裁剪的概念及其在图像处理中的作用

在数字图像处理中，填充和裁剪是两种常用的操作技术，它们在图像编辑和图像分析中扮演着重要角色。填充技术通常用于图像背景处理，边缘增强或者创建特殊效果，它涉及到像素颜色的填充，可以是单一颜色，也可以是基于某种算法的渐变色。而裁剪则是用于选择图像中感兴趣的区域，去除不需要的部分，这在图像预处理和图像分析中非常有用。

7.1.2 常见的填充与裁剪算法

常见的填充算法包括基于颜色的简单填充、基于区域的智能填充（如 Flood Fill 算法），以及基于边缘检测的复杂填充。裁剪技术通常涉及确定裁剪区域的边界，并将该区域之外的像素删除。高级的裁剪技术可能包括对裁剪区域进行图像插值，以保持图像质量。

7.2 Delphi实现图像填充与裁剪的方法

7.2.1 使用TBitmap类进行填充与裁剪

在Delphi中，TBitmap类提供了 Canvas.FillRect 和 Canvas.Cls 等方法来进行图像的填充操作。通过设置 Canvas.Pen 和 Canvas.Brush 属性，可以指定填充的颜色和样式。对于裁剪，TBitmap提供了 Bitmap.SetSize 方法，可以指定裁剪后图像的大小。

procedure FillAndCropImage(Bitmap: TBitmap);
var
  Rect: TRect;
begin
  // 使用TBitmap的Canvas进行填充操作
  with Bitmap.Canvas do
  begin
    // 设定背景填充为白色
    Brush.Color := clWhite;
    // 填充整个图像区域
    FillRect(Rect);
    // 更复杂的填充操作可以使用自定义逻辑
    // ...
  end;

  // 设定裁剪区域
  Rect := Rect(50, 50, 200, 200);
  // 裁剪图像到指定区域
  Bitmap.SetSize(Rect.Right - Rect.Left, Rect.Bottom - Rect.Top);
  Bitmap.Canvas.CopyRect(Rect, Bitmap.Canvas, Rect);
end;

7.2.2 高级填充与裁剪技术的应用

为了提高填充和裁剪的效率，可以考虑实现一些优化策略，例如使用双缓冲技术减少屏幕闪烁、应用硬件加速来加快处理速度。还可以利用图像处理库如Graphics32提供的高级算法来获得更好的填充和裁剪效果。

// 使用双缓冲技术减少屏幕闪烁
procedure DoubleBufferedPainting;
var
  MemBitmap, DisplayBitmap: TBitmap;
begin
  MemBitmap := TBitmap.Create;
  DisplayBitmap := TBitmap.Create;
  try
    MemBitmap.Width := Canvas.Width;
    MemBitmap.Height := Canvas.Height;

    // 在内存中的Bitmap上进行复杂的填充操作
    // ...

    // 将内存中的Bitmap绘制到显示区域
    Canvas.CopyRect(Canvas.ClipRect, MemBitmap.Canvas, Canvas.ClipRect);
  finally
    DisplayBitmap.Free;
    MemBitmap.Free;
  end;
end;

7.3 填充与裁剪技术在实际案例中的运用

7.3.1 图像拼接与拼图游戏中的应用

在图像拼接应用中，填充技术可以用来填补拼接后图像边缘的不连续部分，例如使用邻近像素的平滑过渡进行填充，以增强拼接效果的自然度。在拼图游戏中，裁剪技术则被用来创建不同形状的拼图块，并从原始图像中截取这些拼图块的图片。

7.3.2 图像压缩与网络传输中的应用

在图像压缩和网络传输场景中，填充和裁剪技术也发挥着重要作用。例如，当需要减小文件大小以加快网络传输时，可以裁剪掉图像中不重要的部分，或者对图像进行适当的缩放处理。填充技术可以用来为缩放后的图像边缘添加合适的颜色填充，避免出现未定义的像素值。

填充和裁剪技术的应用不仅限于上述几个案例，它们在数字图像处理中有着广泛的应用场景，如照片编辑、图像复原、图像增强等。理解这些基本操作的原理和实现方法对于从事图像处理的开发者来说至关重要。

本文还有配套的精品资源，点击获取

简介：本文深入探讨了Delphi中的图片处理技术，特别是在二值化和任意角度旋转的应用。二值化能够将图像简化为黑白两色，突出边缘细节，常用于图像识别等场景。任意角度旋转则是处理图像时的常见需求，例如在特定项目中用于检测屏幕缺陷。本文指导如何通过Delphi中的Graphics32库和VCL的TBitmap类实现这些功能，并通过创建Delphi项目来具体实践二值化和旋转技术。

本文还有配套的精品资源，点击获取