
这是一组由9830个圆圈构成的美丽图案,每一个圆圈有一个复杂数学公式来确定其中:
- X(k),Y(k) : 表示圆心坐标
- R(k) :表示半径

下面我们让Python来画出这个美丽的图案
from math import pi,sin,cos
import matplotlib.pyplot as plt
plt.style.use('seaborn-darkgrid')
def X(k):
result=sin(pi*k/20000)**12*(1/2*cos(31*pi*k/10000)**16*
sin(6*pi*k/10000)+1/6*sin(31*pi*k/10000)**20)+3*k/20000+\
cos(31*pi*k/10000)**6*sin(pi/2*((k-10000)/10000)**7-pi/5)
return result
def Y(k):
result=-9/4*cos(31*pi*k/10000)**6*cos(pi/2*((k-10000)/10000)**7-pi/5)*\
(2/3+(sin(pi*k/20000)*sin(3*pi*k/20000))**6)+3/4*\
cos(3*pi*(k-10000)/100000)**10*cos(9*pi*(k-10000)/100000)**10*\
cos(36*pi*(k-10000)/100000)**14+7/10*((k-10000)/10000)**2
return result
def R(k):
result=sin(pi*k/20000)**10*(1/4*cos(31*pi*k/10000+25*pi/32)**20+
1/20*(cos(31*pi*k/10000)**2))+1/30*(3/2-cos(62*pi*k/10000)**2)
return result
plt.figure(figsize=(6, 10),dpi=80)
for k in range(1,9831):
circle = plt.Circle((X(k), Y(k)), R(k),linewidth=0.2,color='black', fill=False)
plt.gcf().gca().add_artist(circle)
plt.xlim(-1.25, 2)
plt.ylim(-3, 1.7)
plt.show(); 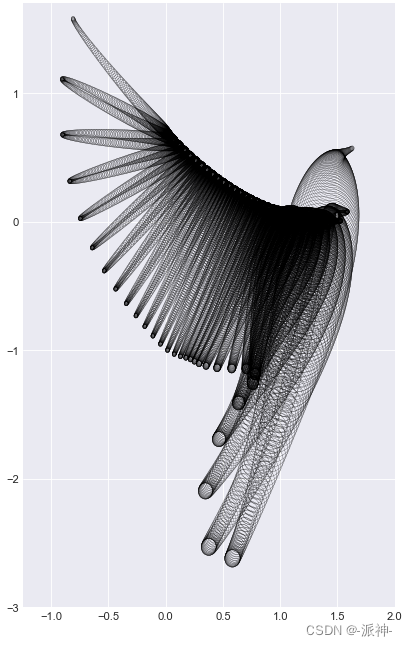




























 1292
1292

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










