数据结构学习笔记——图(一）

ps：此文章只是为了总结学习数据结构笔记，便于以后忘记查阅，因此部分图片会借用书上的图片，望理解。
  在前面的总结中线性表结构，元素之间是被串起来的，仅有线性关系，每个数据元素只有一个直接前驱和一个直接后继。在树型结构中，元素之间有着明显的层次关系，每一层上的数据元素可能和下一层上的数据元素相关，只能和上一层中一个数据元素相关。可在现实中不会有那么直接一对一，一对多的数据关系，而可能会更复杂也就是下面的图，在图形结构中结点间的关系可以是任意的，任意两元素间都可能相关。

（一） 图的定义

  图（graph）是由顶点的有穷非空集合和顶点之间边的集合组成，通常表示为：G（V，E），其中 G 表示一个图，V 是图 G 中顶点的集合，E是图 G 中边的集合。对于上述定义，我们需要明确以下几点：

• 线性表中我们把数据元素叫元素，树中将数据元素叫结点，在图中数据元素，我们称之为顶点（Vertex）。
• 在图结构中，不允许没有顶点。在定义中，若 V 是顶点的集合，则强调了顶点集合 V 有穷非空。
• 在图中，任意两个顶点间都可能有关系，顶点间的逻辑关系用边来表示，边集可以为空。

  无向边：若顶点 vi 到 vj 之间都没有方向，则称这条边胃无向边 （Edge），用无序偶对（ vi，vj）来表示。如果两个图中任意两顶点间的边都是无向边则该图为无向图（Undirected graphs)。如下左图所示，
  对于下图中无向图 G1来说 ，G1= (V1，{E1})，，其中顶点集合 V1={A，B，C，D}; 边集合 E1={ (A,B) ，(B,C) , (C,D)，(D,A) , (A,C) }

  有向边:若从顶点 Vi 到 Vj 的边有方向，则称这条边为有向边，也称为弧( Arc ).。用有序偶<Vi. Vj>来表示>。若图中任意两个顶点间的边都是有向边，则该图称为有向图（Directed graphs）。上图中右侧为有向图。连接顶点 A 到 D 的有向边就是弧， A 是弧尾， D 是弧头，<A, D>表示弧， 注意不能写成<D，A>。
  在无向图中，如果任意两顶点间都存在边，则称该图为无向完全图。含有 n 个顶点的无向完全图又 (n *（n-1)) / 2条边。有些图的边或弧具有与他相关的数字，与图的边或弧相关的数叫权（Weight），这种带权的图通常称为网（Network）。

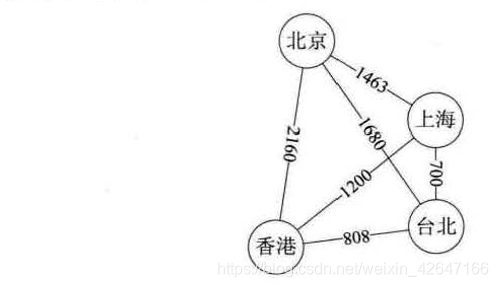
  图中顶点之间有邻接点、依附的概念。无向图顶点的边数叫做度，有向图顶点分入度和出度。
  图中顶点间存在路径，两顶点存在路径则说明是连通的，如果路径最终回到起始点则称为环， 当中不重复叫简单路径。若任意两顶点都是连通的，则图就是连通图， 有向则称强连通图。 图中有子图 ，若子图极大连通则就是连通分量， 有向的则称强连通分量。
  无向图中连通旦 n 个顶点 n-1 条边叫生成树。有向图中一顶点入度为。其余顶点入度为 1 的叫有向树。一个有向图由若干棵有向树构成生成森林。

（二） 图的基本操作

ADT 图（Graph）
Data
	顶点的有穷非空集合边的集合
Operation
	CreateGraph(*G，V，VR ) 		:按照顶点集 v 和边孤集 VR 的定义构造图G。 
	DestroyGraph(*G) 			:图 G 存在则销毁。 
	LocateVex(G, u)				:若图 G 中存在顶点u，则返回图中的位置。
	GetVex(G,v)					:返回图 G 中顶点 v 的值。 
	PutVez(G, v, value)			:将图 G 中顶点 v 赋位 value。
	FirstAdjVex(G，*v) 			:返回顶点 v 的一个邻接顶点，若顶点在 G 中无邻接顶点返回空。
	NextAdjVex(G, v，*w) 		:返回顶点 v 相对于顶点 w 的丁一个邻接顶点，若 w 是v 的最后一个邻接点则返回"空" 。
	InSertVex(*G，v ) 			:在图 G 中增添新顶点 v。
	DeleteVex(*G，v) 			:删除图 G 中顶点 v 及其相关的孤。
	InsertArc(*G，v，w) 			:在图 G 中增添弧<v,w>若 G 是无向图，还需要增添对称孤<w，v>。 
	DeleteArc(*G，v，w)			:在图 G 中删除孤<v，w>，若 G 是无向圈，则还删除对称孤<w，v>。 
	DFSTraverse(G) 				:对图 G 中进行深度优先遍历，在遍历过程对每个顶点调用。
	HFSTraverse(G) 				:对图 G 中进衍广度优先遍历.在遍历过程对每个顶点调用。
endADT

（三） 图的存储结构

1. 邻接矩阵存储

  图的邻接矩阵 (Adjacency Matrix) 存储方式是用两个数组来表示图。一个一维数组存储圈中顶点信息，一个二维数组〈称为邻接矩阵)存储图中的边或弧的信息。

  设置两个数组 vertex[4]={ vo，v1， v2， v3} ， 边数组 arc[4][4]，如上图所示，无向图的边数组是一个对称矩阵。我们可从上面的矩阵获得如下信息：
  1、.我们要判定任意两顶点是否有边无边就非常容易了。
  2、 我们要知道某个顶点的度，其实就是这个顶点 Vi在邻接矩阵中第 i 行(或第 i 列)的元素之和。比如顶点 V1的度就是 1+0+1+0=2。
  3、 求顶点 Vi 的所有邻接点就是将矩阵中第 1 行元素扫描一遍， arc[ i ][ j ]为 1 就是 邻接点。
  下面是一个有向图的例子：

  因为其是有向图，因此此矩阵不对称，由 V1到 V0 有弧，得到 arc[1][0]=1 ，而 V0到 V1没有弧，因此 arc[0][1]=0。有向图讲究入度与出度，顶点 v1 的入度为 1，正好是第 V1列各数之和。顶点 V1 的出度为 2，即第 V1 行的各数之和。
  每条边上带有权的图叫做网，我们可以在他的邻接矩阵中存入两个顶点的权值，“ ∞ ”作为两个顶点不连通：

  邻接矩阵存储结构：

typedef char VertexType; /* 顶点类型应由用户定义  */
typedef int EdgeType; /* 边上的权值类型应由用户定义 */
#define MAXVEX 100 /* 最大顶点数，应由用户定义 */
#define INFINITY 65535
typedef struct
{
   
	VertexType vexs[MAXVEX]; /* 顶点表 */
	EdgeType arc[MAXVEX][MAXVEX];/* 邻接矩阵，可看作边表 */
	int numNodes, numEdges; /* 图中当前的顶点数和边数  */
}MGraph;

  无向网图的创建代码：

/* 建立无向网图的邻接矩阵表示 */
void CreateMGraph(MGraph *G)
{
   
	int i,j,k,w;
	printf("输入顶点数和边数:\n");
	scanf("%d,%d",&G->numNodes,&G->numEdges); /* 输入顶点数和边数 */
	for(i = 0;i <G->numNodes;i++) /* 读入顶点信息,建立顶点表 */
		scanf(&G->vexs[i]);
	for(i = 0;i <G->numNodes;i++)
		for(j = 0;j <G->numNodes;j++)
			G->arc[i][j]=INFINITY;	/* 邻接矩阵初始化 */
	for(k = 0;k <G->numEdges;k