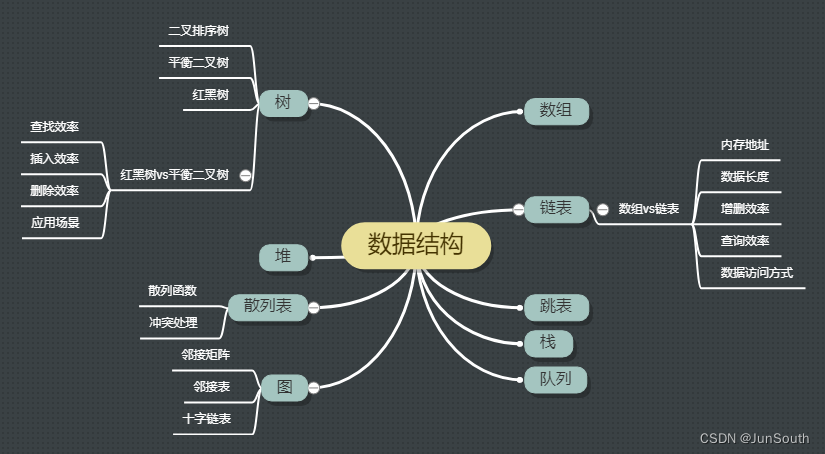
一、表
1.1、散列表
也叫哈希表,把数据分散在列表中,依赖于数组下标访问的特性,数组的一种拓展。
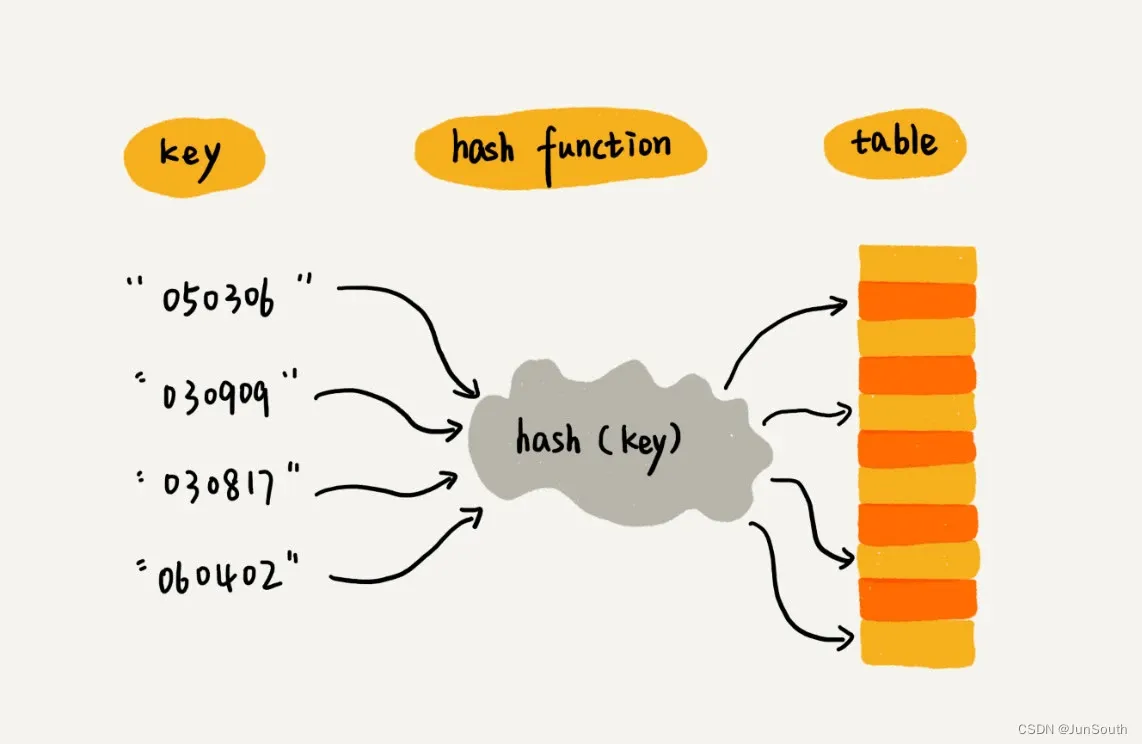
散列思想:
即映射思想,用键值对来保存信息,键(key)和值(value)间的映射法则叫散列函数(Hash函数),通过散列函数得到的值叫散列值(Hash值)。散列函数:
散列函数根据key生成一个对应的散列值(数组下标),将key的信息保存到该数组下标对应的内存空间。
构造散列函数三个基本要求
1.通过散列函数得到的散列值是一个非负整数,因为散列值是数组下标。
2.如果key1 == key2,则hash(key1) == hash(key2),保证同样的key只对应一个散列值。
3.如果key1!= key2,则hash(key1)!= hash(key2),保证同样的key只对应一个散列值。散列冲突:
不同的key经过散列函数散列后,会出现相同的散列值。同义词:
这些发生冲突的不同关键字称为同义词。装填因子:
散列表的装填因子一般记为α,定义为一个表的装满程度。

散列冲突(Hash冲突)的解决
不同的key经过散列函数散列后,会出现相同的散列值。
1.开放寻址法
出现一个重复散列值,寻找空闲位置插入。
1.1线性探测法
从当前已占用位置开始,寻找下一个空闲位置( hash(key)+0,hash(key)+1,hash(key)+2……),直到找到为止。
1.2二次探测
探测的步长就变成了线性探测的"二次方"(hash(key)+0,hash(key)+12,hash(key)+22……)。
1.3双重散列
用一组散列函数(hash1(key),hash2(key),hash3(key)……),第一个散列函数计算的存储位置被占用,用第二个散列函数,依次类推,直到找到空闲的存储位置。
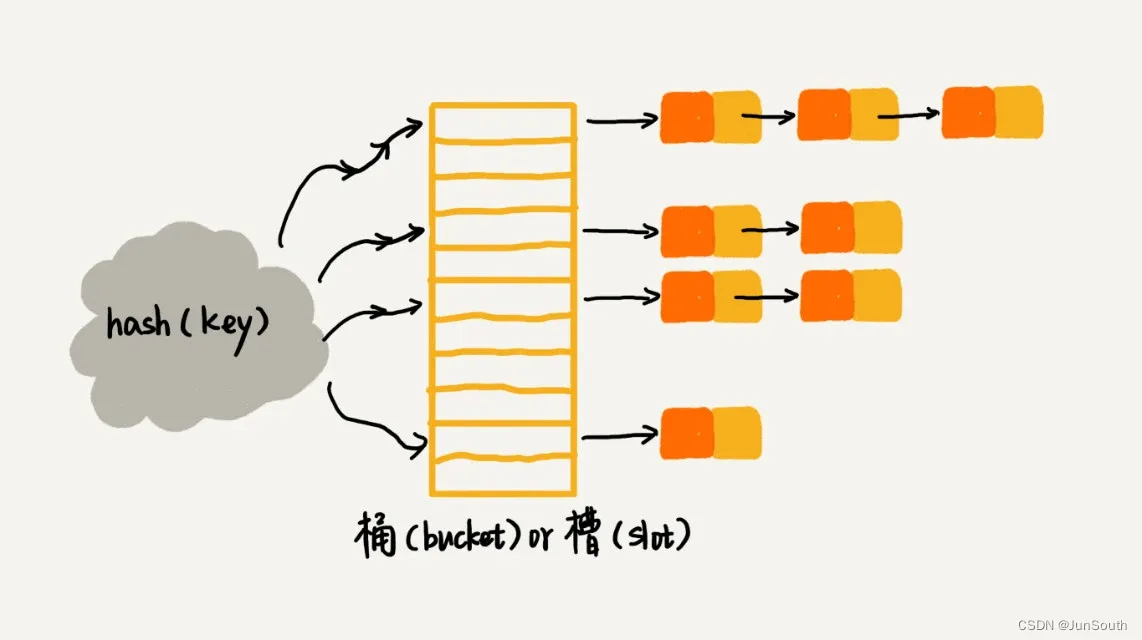
2.链表法
本质是数组加链表,数组保存的是每个槽的头链表。每个槽(slot)"对应一条链表,散列值相同元素放到同槽位对应的链表中。
二、树
2.1、二叉树
非线性数据结构,由多个节点组成的有层次关系集合,像一颗倒挂的树。
节点的度:一个结点含有子树的个数。
树的度:节点的度的最大值。
叶子节点(终端节点):度为0的节点。
父节点(双亲节点):一个节点的前驱节点称为此节点的父节点。
子节点(孩子节点):一个节点的后继节点称为此节点的子节点。
根节点:树中没有父节点的节点。
节点层次:从根节点开始往下,根节点为1层,以此类推。
树的高度:节点的最大层数。
树的深度:根节点到指定节点的最长路径的节点数。
2.1.1、二叉树种类
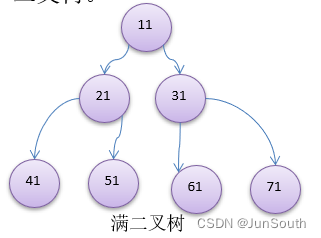
2.1.1.1、满二叉树
二叉树的所有叶子节点都在最后一层,且结点总数=2^n-1,n为层数。
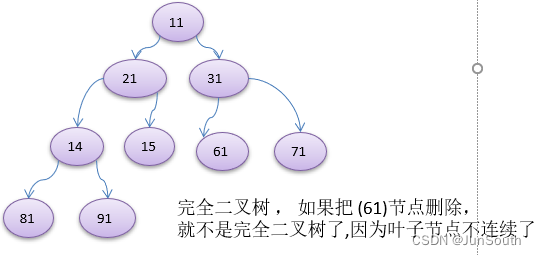
2.1.1.2、完全二叉树
所有叶子节点都在最后一层或者倒数第二层,且最后一层的叶子节点在左边连接,倒数第二层的叶子节点在右边连接。
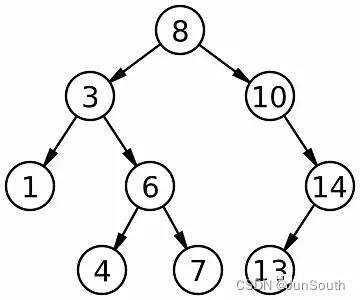
2.1.1.3、二叉搜索树(二叉排序树、二叉查找树)
左子树上所有节点的值均小于它的根节点的值,右子树上所有节点的值均大于它的根节点的值。
import java.util.LinkedList;
import java.util.Queue;
/**
* 二分搜索树
*/
public class MyBST<E extends Comparable<E>> {
private Node root;
private int size;
public MyBST(){
this.root = null;
this.size = 0;
}
// 向二分搜索树中添加新的元素e
public void add(E e){
root = add(root,e);
}
// 向以node为根的二分搜索树中插入元素e,递归算法。 返回插入新节点后二分搜索树的根
private Node add(Node node, E e){
if(node == null){
size = size +1;
return new Node(e);
}
if(e.compareTo(node.e) < 0){
node.left = add(node.left,e);
}else if(e.compareTo(node.e) > 0){
node.right = add(node.right,e);
}
return node;
}
// 看二分搜索树中是否包含元素e
public boolean contains(E e){
return contains(root, e);
}
// 看以node为根的二分搜索树中是否包含元素e,递归算法
public boolean contains(Node node,E e){
if(node==null){
return false;
}
if(e.compareTo(node.e) < 0){
return contains(node.left,e);
}else if(e.compareTo(node.e) > 0){
return contains(node.right,e);
}else {
return true;
}
}
// 二分搜索树的前序遍历
public void preOrder(){
if(root==null){
System.out.println("空树");
}else {
preOrder(root);
}
}
// 前序遍历以 node为根的二分搜索树, 递归算法
public void preOrder(Node node){
if(node == null){
return;
}
System.out.println(node.e);
preOrder(node.left);
preOrder(node.right);
}
// 二分搜索树的中序遍历
public void inOrder(){
inOrder(root);
}
// 中序遍历以node为根的二分搜索树, 递归算法
private void inOrder(Node node){
if(node == null){
return;
}
inOrder(node.left);
System.out.println(node.e);
inOrder(node.right);
}
// 二分搜索树的后序遍历
public void postOrder(){
postOrder(root);
}
// 后序遍历以node为根的二分搜索树, 递归算法
private void postOrder(Node node){
if(node == null){
return;
}
postOrder(node.left);
postOrder(node.right);
System.out.println(node.e);
}
// 二分搜索树的层序遍历
public void levelOrder(){
if(root == null){
return;
}
Queue<Node> que = new LinkedList<>();
que.add(root);
while(!que.isEmpty()){
Node cur = que.remove();
System.out.println(cur.e);
if(cur.left != null){
que.add(cur.left);
}
if(cur.right != null){
que.add(cur.right);
}
}
}
// 从二分搜索树中删除元素为e的节点
public void remove(E e){
root = remove(root,e);
}
// 删除掉以node为根的二分搜索树中值为e的节点, 递归算法
// 返回删除节点后新的二分搜索树的根
public Node remove(Node node,E e){
if( node == null ){
return null;
}
if(e.compareTo(node.e) < 0){
node.left = remove(node.left,e);
return node;
}else if(e.compareTo(node.e)>0){
node.right = remove(node.right,e);
return node;
}else {
if(node.left == null){
Node rightNode = node.right;
node.right = null;
size = size-1;
return rightNode;
}
if(node.right == null){
Node leftNode = node.left;
node.left = null;
size = size-1;
return leftNode;
}
// 待删除节点左右子树均不为空的情况
// 找到比待删除节点大的最小节点,即待删除节点右子树的最小节点,用这个节点顶替待删除节点的位置
Node successor = minimum(node.right);
successor.right = removeMin(node.right);
successor.left = node.left;
node.left = node.right = null;
return successor;
}
}
// 返回以node为根的二分搜索树的最小值所在的节点
private Node minimum(Node node){
if(node.left == null){
return node;
}
return minimum(node.left);
}
// 删除掉以node为根的二分搜索树中的最小节点,返回删除节点后新的二分搜索树的根
private Node removeMin(Node node){
if(node.left == null){
Node rightNode = node.right;
node.right = null;
size --;
return rightNode;
}
node.left = removeMin(node.left);
return node;
}
private class Node{
public E e;
public Node left;
public Node right;
public Node(E e){
this.e = e;
this.left = null;
this.right = null;
}
}
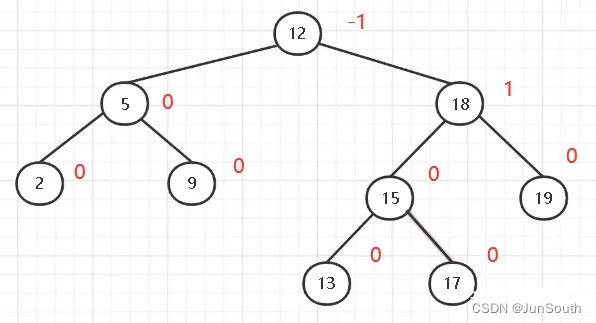
}2.1.1.4、平衡二叉树
每个结点的左子树的高度减去右子树的高度的绝对值不超过1
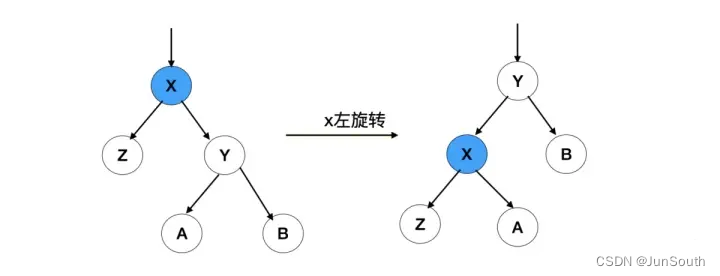
左旋:
根节点的右侧往左拉,原右子节点成新的父节点,原右节子点的左子节点给降级的根节点当右子节点。
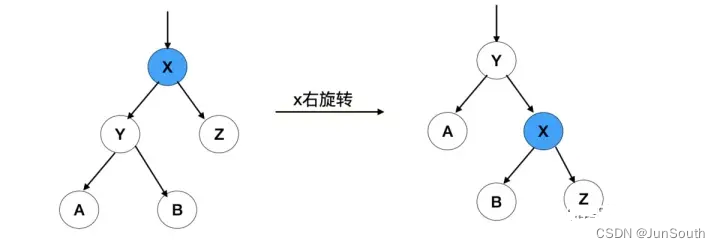
右旋:
根节点的左侧往右拉,原左子节点成新的父节点,原左子节点的右子节点给降级的根节点当左子节点。
import java.util.ArrayList;
/**
* 平衡二叉树
*/
public class MyAVLTree<K extends Comparable<K>, V> {
private Node root;
private int size;
public MyAVLTree(){
root = null;
size = 0;
}
// 判断该二叉树是否是一棵二分搜索树。
public boolean isBST(){
ArrayList<K> keys = new ArrayList<>();
inOrder(root, keys);
for(int i = 1 ; i < keys.size() ; i ++){
if(keys.get(i - 1).compareTo(keys.get(i)) > 0){
return false;
}
}
return true;
}
//中置遍历,顺序取出各个节点。
private void inOrder(Node node, ArrayList<K> keys){
if(node == null){
return;
}
inOrder(node.left, keys);
keys.add(node.key);
inOrder(node.right, keys);
}
// 判断该二叉树是否是一棵平衡二叉树。
public boolean isBalanced(){
return isBalanced(root);
}
// 判断以Node为根的二叉树是否是一棵平衡二叉树,递归算法。
private boolean isBalanced(Node node){
if(node == null){
return true;
}
int balanceFactor = getBalanceFactor(node);
if(Math.abs(balanceFactor) > 1){
return false;
}
return isBalanced(node.left) && isBalanced(node.right);
}
// 获得节点node的平衡因子
private int getBalanceFactor(Node node){
if(node == null){
return 0;
}
return node.left.height- node.right.height;
}
// 对节点y进行向右旋转操作,返回旋转后新的根节点x。
// y x
// / \ / \
// x T4 向右旋转 (y) z y
// / \ - - - - - - - -> / \ / \
// z T3 T1 T2 T3 T4
// / \
// T1 T2
private Node rightRotate(Node y) {
Node x = y.left;
Node T3 = x.right;
// 向右旋转过程
x.right = y;
y.left = T3;
// 更新height
y.height = Math.max(y.left.height,y.right.height) + 1;
x.height = Math.max(x.left.height,x.right.height) + 1;
return x;
}
// 对节点y进行向左旋转操作,返回旋转后新的根节点x。
// y x
// / \ / \
// T1 x 向左旋转 (y) y z
// / \ - - - - - - - -> / \ / \
// T2 z T1 T2 T3 T4
// / \
// T3 T4
private Node leftRotate(Node y) {
Node x = y.right;
Node T2 = x.left;
// 向左旋转过程
x.left = y;
y.right = T2;
// 更新height
y.height = Math.max(y.left.height,y.right.height) + 1;
x.height = Math.max(x.left.height,x.right.height) + 1;
return x;
}
// 向二分搜索树中添加新的元素(key, value)。
public void add(K key, V value){
root = add(root, key, value);
}
// 向以node为根的二分搜索树中插入元素(key, value), 递归算法。
// 返回插入新节点后二分搜索树的根。
private Node add(Node node, K key, V value){
if(node == null){
size = size+1;
return new Node(key, value);
}
if(key.compareTo(node.key) < 0){
node.left = add(node.left, key, value);
} else if(key.compareTo(node.key) > 0){
node.right = add(node.right, key, value);
} else{ // key.compareTo(node.key) == 0
node.value = value;
}
// 更新height
node.height = 1 + Math.max(node.left.height,node.right.height);
// 计算平衡因子
int balanceFactor = getBalanceFactor(node);
// 平衡维护
// LL
if (balanceFactor > 1 && getBalanceFactor(node.left) >= 0){
return rightRotate(node);
}
// RR
if (balanceFactor < -1 && getBalanceFactor(node.right) <= 0){
return leftRotate(node);
}
// LR
if (balanceFactor > 1 && getBalanceFactor(node.left) < 0) {
node.left = leftRotate(node.left);
return rightRotate(node);
}
// RL
if (balanceFactor < -1 && getBalanceFactor(node.right) > 0) {
node.right = rightRotate(node.right);
return leftRotate(node);
}
return node;
}
// 返回以node为根节点的二分搜索树中,key所在的节点。
private Node getNode(Node node, K key){
if(node == null){
return null;
}
if(key.equals(node.key)){
return node;
}else if(key.compareTo(node.key) < 0){
return getNode(node.left, key);
}else { // if(key.compareTo(node.key) > 0)
return getNode(node.right, key);
}
}
public boolean contains(K key){
return getNode(root, key) != null;
}
public V get(K key){
Node node = getNode(root, key);
return node == null ? null : node.value;
}
public void set(K key, V newValue){
Node node = getNode(root, key);
if(node == null){
throw new IllegalArgumentException(key + " 不存在!");
}
node.value = newValue;
}
// 返回以node为根的二分搜索树的最小值所在的节点
private Node minimum(Node node){
if(node.left == null){
return node;
}
return minimum(node.left);
}
// 从二分搜索树中删除键为key的节点
public V remove(K key){
Node node = getNode(root, key);
if(node != null){
root = remove(root, key);
return node.value;
}
return null;
}
private Node remove(Node node, K key){
if( node == null ){
return null;
}
Node retNode;
if( key.compareTo(node.key) < 0 ){
node.left = remove(node.left , key);
retNode = node;
}else if(key.compareTo(node.key) > 0 ){
node.right = remove(node.right, key);
retNode = node;
}else{ // key.compareTo(node.key) == 0
// 待删除节点左子树为空的情况
if(node.left == null){
Node rightNode = node.right;
node.right = null;
size = size-1;
retNode = rightNode;
}
// 待删除节点右子树为空的情况
else if(node.right == null){
Node leftNode = node.left;
node.left = null;
size = size-1;
retNode = leftNode;
}else{ // 待删除节点左右子树均不为空的情况.
// 找到比待删除节点大的最小节点, 即待删除节点右子树的最小节点.
// 用这个节点顶替待删除节点的位置.
Node successor = minimum(node.right);
successor.right = remove(node.right, successor.key);
successor.left = node.left;
node.left = node.right = null;
retNode = successor;
}
}
if(retNode == null){
return null;
}
// 更新height
retNode.height = 1 + Math.max(retNode.left.height,retNode.right.height);
// 计算平衡因子
int balanceFactor = getBalanceFactor(retNode);
// 平衡维护
// LL
if (balanceFactor > 1 && getBalanceFactor(retNode.left) >= 0){
return rightRotate(retNode);
}
// RR
if (balanceFactor < -1 && getBalanceFactor(retNode.right) <= 0){
return leftRotate(retNode);
}
// LR
if (balanceFactor > 1 && getBalanceFactor(retNode.left) < 0) {
retNode.left = leftRotate(retNode.left);
return rightRotate(retNode);
}
// RL
if (balanceFactor < -1 && getBalanceFactor(retNode.right) > 0) {
retNode.right = rightRotate(retNode.right);
return leftRotate(retNode);
}
return retNode;
}
private class Node{
public K key;
public V value;
public Node left;
public Node right;
public int height;
public Node(K key, V value){
this.key = key;
this.value = value;
left = null;
right = null;
height = 1;
}
}
}2.1.1.5、平衡二叉树—AVL树
带了平衡功能的二叉查找树(二叉排序树,二叉搜索树),每个结点的左右子树的高度之差的绝对值(平衡因子)最多为1。
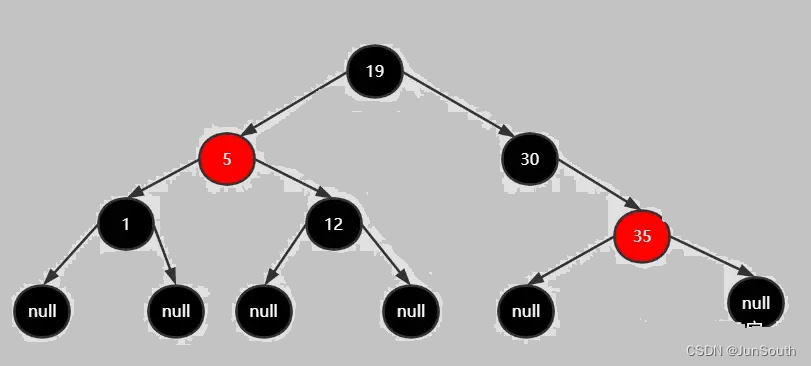
2.1.1.6、平衡二叉树—红黑树
每个结点非红即黑,根节点是黑色的,每个红色结点的两个子结点都是黑色(无连续的红结点)。
从任一结点到其每个叶子的所有路径都包含相同数目的黑结点。
保证最长路径不超过最短路径的2倍,降低了插入和旋转的次数,增删的结构中性能比AVL树更优。
2.1.2、二叉树的遍历

2.1.2.1、前序遍历(先根遍历、根左右)
先输出父节点,再遍历左子树和右子树。
2.1.2.2、中序遍历(中根遍历、左根右)
先遍历左子树,再输出父节点,再遍历右子树。
2.1.2.3、后序遍历(后根遍历、左右根)
先遍历左子树,再遍历右子树,最后输出父节点。
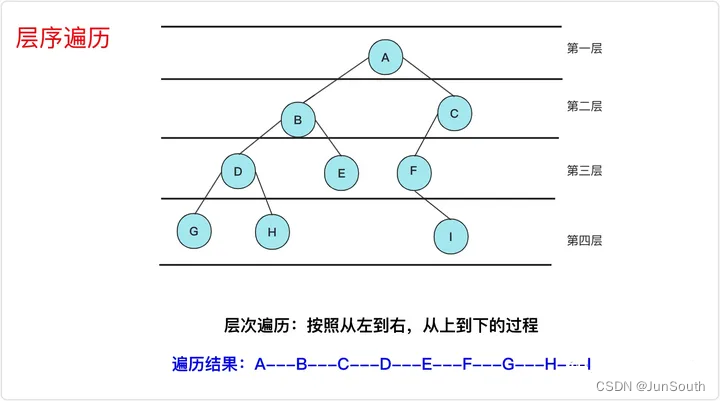
2.1.2.4、层序遍历
按二叉树的层次从上至下从左至右进行遍历
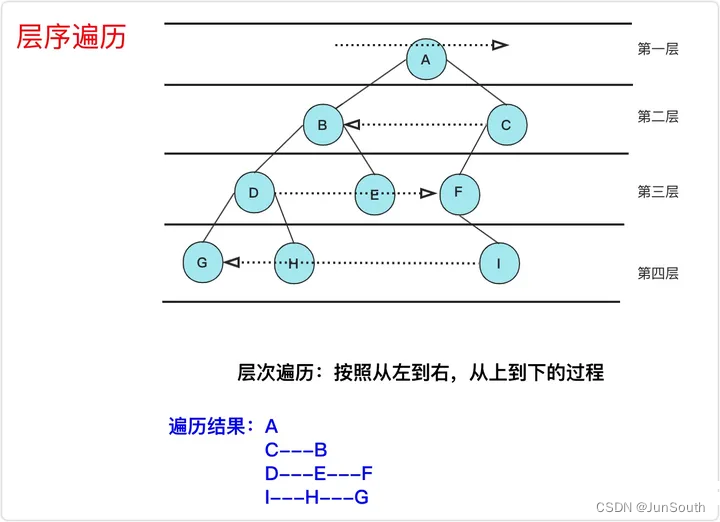
2.1.2.5、S形层序遍历
奇数层从左往右打印,偶数层从右向左打印。
2.2、二叉树—红黑树
三、图
3.1、图
图(Graph)一种多对多的关系,由节点(或顶点)和连接这些节点的边(或弧)组成。
可用来表示各种实际应用场景中的关系和连接,如网络路由、社交网络分析、交通运输、电路设计等。
图也是许多算法的基础,如最短路径算法、最小生成树算法、拓扑排序算法等。
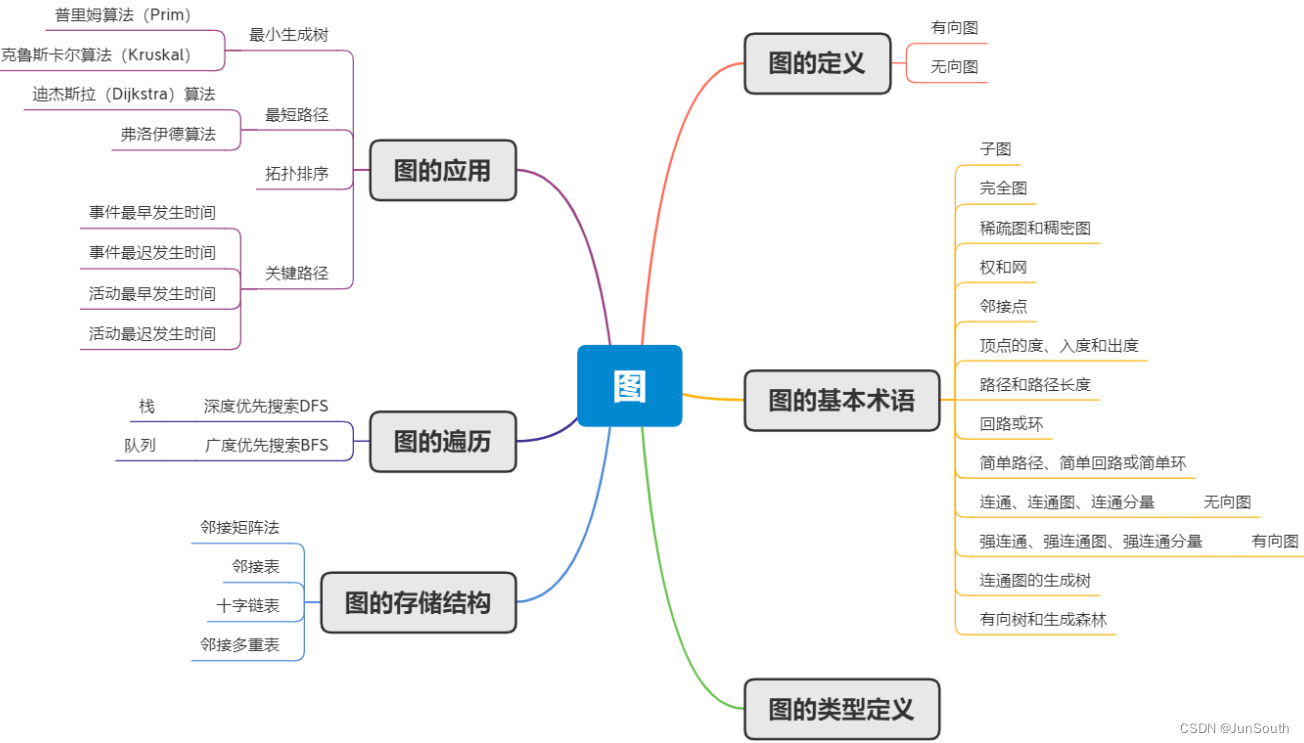
图的基本概念
顶点(Vertex):图中的点被称为顶点,每个顶点可以代表一个实体,如人、物体、事件等。
边(Edge):连接两个顶点的线段称为边。边可以表示这两个顶点之间的关系或连接。
邻接点(Adjacent Vertices):与一条边相连的两个顶点称为该边的邻接点。
路径(Path):从一个顶点到另一个顶点的一系列边和顶点称为路径。
环(Cycle):一条路径,其中某个顶点是通过边连接回到路径中的先前顶点,称为环。
无向图(Undirected Graph):边没有方向,即两个顶点可以通过一条边相互连接。
有向图(Directed Graph):边有方向,即一个顶点可以通过一条边指向另一个顶点。
简单图(Simple Graph):不包含重复边和重复顶点的图称为简单图。
加权图(Weighted Graph):边带有权重的图称为加权图。权重可以表示距离、成本或其他测量值。
稀疏图(Sparse Graph):边的数量相对较少的图称为稀疏图。
稠密图(Dense Graph):边的数量相对较多的图称为稠密图。
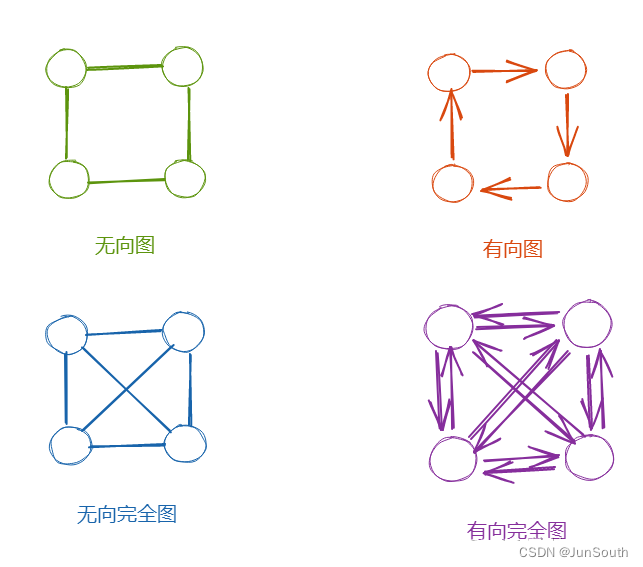
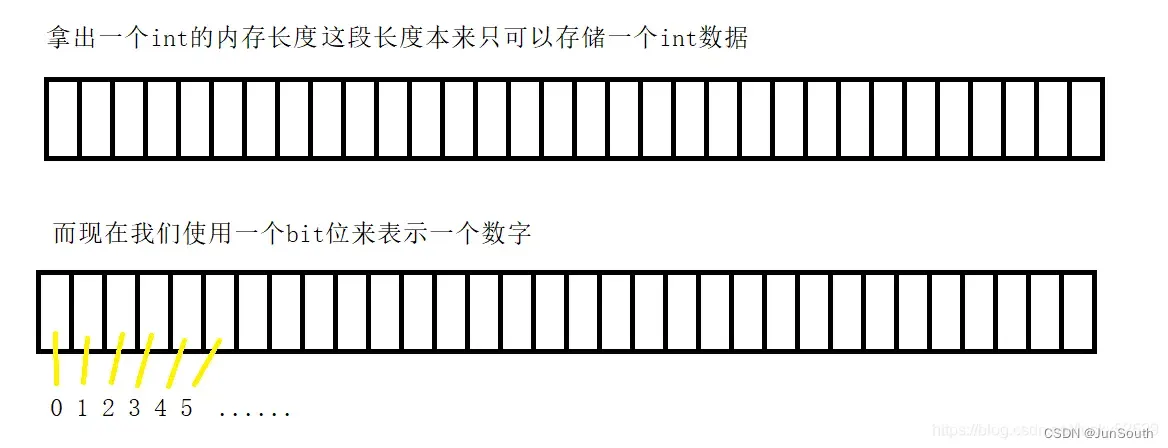
3.2、位图(bitmap)
用一系列位来表示数据,每个位只有两个状态(0或1),在存储大量数据时高效且节省空间。
import java.util.HashSet;
public class Test01 {
public static class BitMap {
//定义long数组,一个元素可以存放64个数,因为long类型是8字节 64位
private long[] bits;
//定义数组长度,需要先给需要存储的数集的最大值 (max+64/64) 表示需要多少个,如 max是63 那个得 1 只需一个元素就可以
//如果是64 得 2,就需要2个元素 因为一个Long64位 存放0-63的数值, 接着是64-127
public BitMap(int max) { bits = new long[(max + 64) >> 6];}
/**
* 保存数值
* 1.num>>6 表示先将目标数值除以64 得到该数值是位于bits数组的第几个,比如63 / 64 = 0 在bit[0] 64/64=1 bit[1]..
* 2.num & 63 表示num % 64 , 即看在该元素的第几位, 2的6次方=64 第7位1000000 所以可以知道求模后肯定余数是1-6位的数,
* 那么与运算 111111 即 63 就能表示1-6的值,也就是余数,也就得到是位于该元素中的第几位了 比如余数0 那么就是第一位 ,
* 1 就是第二位... 确定了这个余数 即第几位,那么我们就用 1l << 余数(1必须要为long型 1L 取值长度才不会越界,int是32位,
* 所以右移63肯定位数不够) 将1右移余数位,比如余数1 那么就1L右移一位,表示在这个位置标1了。
* 3.前面得到了对应在第几个元素中的第几位,最后就是需要在这个元素的这个位置赋值1. 那么就是可以将元素位置bits[num >>6] =
* bits[num >>6] | (1L << (num & 64) 即或运算 前面得到的具体位置,有1 则表示1 所以就给元素的对于位置赋值1了
*/
public void add(int num) {
bits[num >> 6] |= (1L << (num & 63));
}
/**
* 删除数值, 就是将对应的元素中的第几位 将其1改成0
* 1.bits[num >> 6] 元素所在数组的元素, 1L << (num & 63) 64位元素中的第几位 表示存放着num
* 2.对1L << (num & 63) 取反, 就得到一个 1111...01111 即将存放位赋值0 其他为1
* 3.将取反后的数 与bits[num >> 6] 所在元素就行 与运算, 此时其他位都位1 与完元素不变,而num所在位是0 与完则为0,则
* 表示将数组删除
*/
public void delete(int num) {
bits[num >> 6] &= ~(1L << (num & 63));
}
/**
* 判断数值是否包含,那么就是判断 bits[num >> 6] 所在元素的(1L << (num & 63)) 所在位 进行与运算,(1L << (num & 63))
* 所在位为1 其他位都为0 所以与运算后 如果为一 表示bits[num >> 6] 的所在位也是1 那么就返回true
*/
public boolean contains(int num) {
return (bits[num >> 6] & (1L << (num & 63))) != 0;
}
}
public static void main(String[] args) {
int max = 10000;
BitMap bitMap = new BitMap(max);
HashSet<Integer> set = new HashSet<>();
int testTime = 10000000;
for (int i = 0; i < testTime; i++) {
int num = (int) (Math.random() * (max + 1));
double decide = Math.random();
if (decide < 0.333) {
bitMap.add(num);
set.add(num);
} else if (decide < 0.666) {
bitMap.delete(num);
set.remove(num);
} else {
if (bitMap.contains(num) != set.contains(num)) {
System.out.println("Oops!");
break;
}
}
}
for (int num = 0; num <= max; num++) {
if (bitMap.contains(num) != set.contains(num)) {
System.out.println("Oops!");
}
}
}
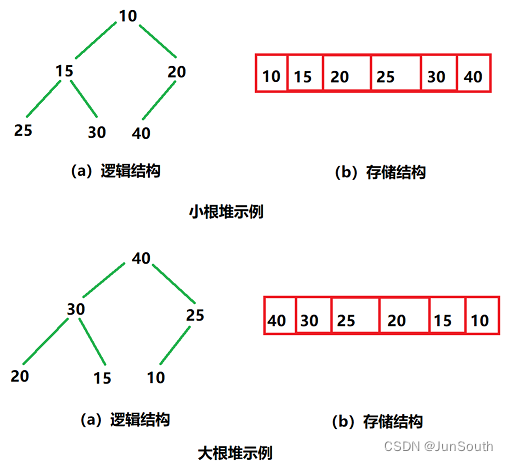
}四、堆(Heap)
堆总是一棵完全二叉树,某个节点的值总是不大于或不小于其父节点的值。





















 2159
2159











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








