协方差分析与交互分析

协方差分析

定义

协方差分析亦称“共变量（数）分析”。方差分析的引申和扩大。基本原理是将线性回归与方差分析结合起来，调整各组平均数和 F 检验的实验误差项，检验两个或多个调整平均数有无显著差异，以便控制在实验中影响实验效应（因变量）而无法人为控制的协变量（与因变量有密切回归关系的变量）在方差分析中的影响。例如，在研究某种教学方法（实验变量）对学业成绩（实验效应）的影响时，被试的原有知识基础同时影响学业成绩，但往往在实验中难以选取具备相同知识基础的被试参加实验，可用协方差分析从学业成绩的总变异中将归因于被试知识基础差异的部分划分出去，便于确切地分析教学方法对学业成绩的影响，其中被试的知识基础就是协变量。

背景

有如下数据

其中第一列为方法、第二列为培训时间，第三列为评分，现在需要控制住培训时间，看不同方法下评分是否有差异。

操作

不同方法下的平均培训时间和平均评分

分析-比较平均值-平均值

因变量为评分和培训时间，自变量是培训方式

结果如下：不同方法下的培训时间和评分

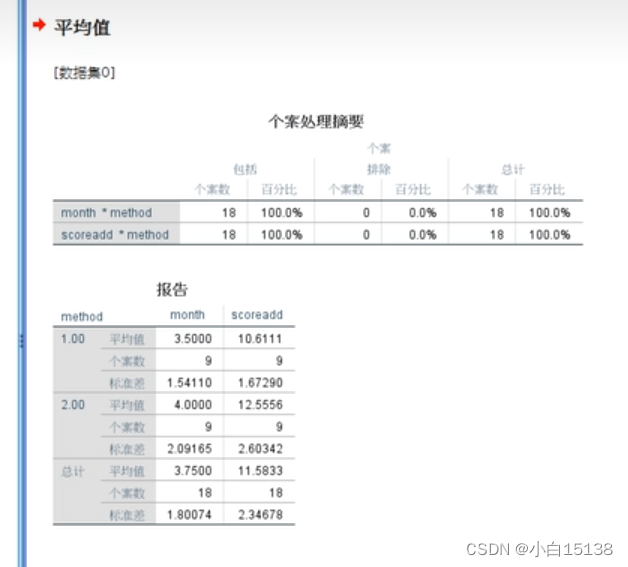
从结果上看培训方式一的评分虽然低于培训方式2，但是培训方式1的培训时间也更低，所以直接通过比较平均值是不能判断哪种培训方式的评分高的，所以需要在控制住培训时间的情况下，分析培训方式不同评分是否有差异。

协方差分析

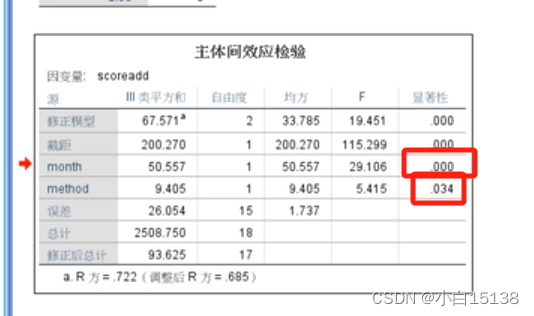
分析-一般线性模型-单变量

因变量为评分，固定因子为方法，协变量为培训时间（即控制变量）

结果如下：从结果中看到month的显著性为0.000说明month是个显著的混杂因素，method的显著性为0.034说明在排除了month的影响后，不同的方法的评分也有显著的差异。

协方差绘图

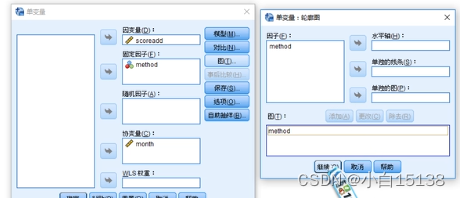
还是SPSS-分析-一般线性模型-单变量

在单变量中配置好因变量和固定因子和协变量后，点击图，把方法配置到水平轴上，点击添加。完成配置


结果如下：此图是排斥了培训时间的混杂干扰后的，方法1和方法2的评分结果对比图

交互作用

定义

交互作用（interaction）是指一个因素各个水平之间反应量的差异随其他因素的不同水平而发生变化的现象。它的存在说明同时研究的若干因素的效应非独立。交互作用的效应可度量一个因素不同水平的效应变化依赖于另一个或几个因素的水平的程度。

参考资料使用SPSS完成两变量交互项显著时的简单效应分析

背景

分析培训方法和培训时间对培训得分的影响，分析培训方法和培训时间的交互项是否显著的影响培训得分

操作步骤

分析-一般线性模型-单变量

配置因变量为培训得分，固定因子为培训方法和培训时间。

点击模型按钮，点击构建项，选中培训方法和培训时间配置到模型中，类型选择交互。

在水平轴上配置培训时间，单独的线条配置培训方法，配置完成后点击添加按钮，完成图形配置。再在水平轴上配置培训方法，单独的线条配置培训时间，配置完成后点击添加按钮，完成图形配置

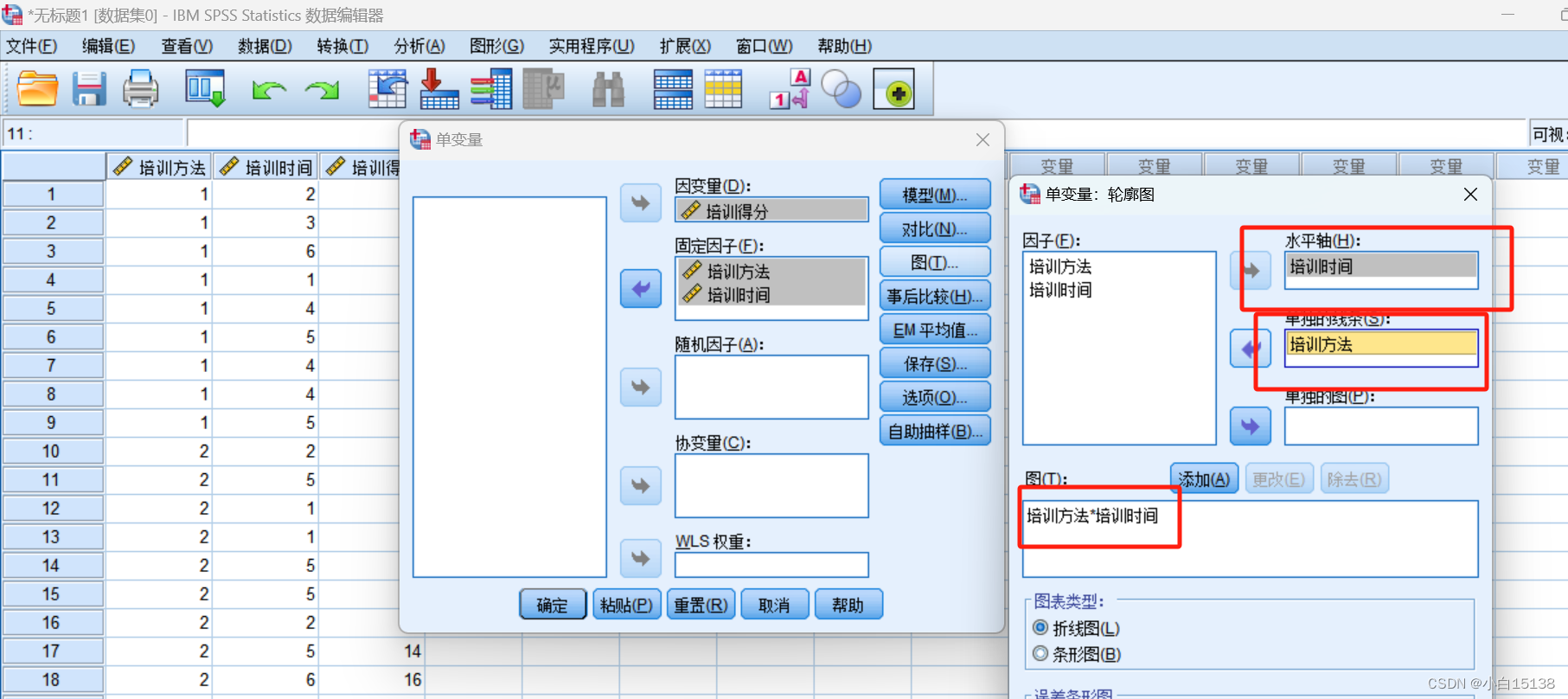
最终结果如下：

选项勾选描述统计

完成配置，点击粘贴按钮，进入到代码页面

把这两段代码写进去插入SPSS的代码中
/EMMEANS=TABLES(培训方法培训时间)COMPARE(培训方法)ADJ(SIDAK)
/EMMEANS=TABLES(培训方法培训时间)COMPARE(培训时间)ADJ(SIDAK)
结果如下：

点击运行按钮，完成所有的操作

结果分析

首先看主体间效应检验，这个是此分析的核心结果，这里显示培训时间和培训方法的交互项是否显著影响培训得分，由图可以看到显著性为0.202大于0.05说明交互项不显著。

之后可以通过成对比较，来看具体的不同的培训时间和不同的培训方法的培训得分的差异是否显著。这里的主要指标是平均值差值以及显著性。按照培训时间和培训方法谁作为控制变量区分总共有两个成对比较。


最后可以通过两个轮廓图来看交互项的影响情况