基于贝叶斯概率模型的变分自编码
贝叶斯模型
机器学习中可以分为两种概率模型,贝叶斯模型和传统概率模型(极大似然估计)
贝叶斯法则
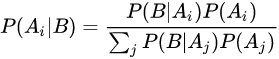
其中P(A|B)是在B发生的情况下A发生的可能性。
A
1
,
A
2
,
.
.
.
,
A
n
A_{1},A_{2},...,A_{n}
A1,A2,...,An为完备事件组,即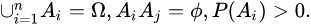
在贝叶斯法则中,每个名词都有约定俗成的名称:
Pr(A)是A的先验概率或边缘概率。之所以称为"先验"是因为它不考虑任何B方面的因素。
Pr(A|B)是已知B发生后A的条件概率,也由于得自B的取值而被称作A的后验概率。
Pr(B|A)是已知A发生后B的条件概率,也由于得自A的取值而被称作B的后验概率。
Pr(B)是B的先验概率或边缘概率,也作标准化常量(normalized constant)。
变分自编码
自动编码器是一种无监督的深度学习模型,由编码器和解码器两部分组成。通过将某种格式的输入数据经过编码器生成中间的隐变量表征,再经过解码器重构原始数据,无需提供类别信息,该网络就可以在中间的隐藏层提取得到数据的低维特征。
变分自编码器则是一种生成式模型,它与自动编码器的关联主要体现在模型的网络架构上,即都包含一个编码器和解码器,但在数学原理上其实有着较为显著的差别。
假定观测数据为 𝑋,隐变量为 𝑧,变分自编码器的基本思想是从中学习出一个概率分布,使得该分布和原始数据分布接近,这样从中采样重构也能得到接近真实的数据,根据贝叶斯公式: P ( z ∣ X ) = P ( X , z ) P ( X ) = P ( X , z ) ∫ P ( X , z ) d z P(z|X)=\frac{P(X,z)}{P(X)}=\frac{P(X,z)}{\int P(X,z) dz} P(z∣X)=P(X)P(X,z)=∫P(X,z)dzP(X,z)
事实上,关于隐变量 𝑧 分布的求解是一个统计推断问题,涉及到积分计算。而在一般情况下,尤其当隐变量处于高维连续空间中时,直接计算较为不易,通常会面临指数级的复杂度,一般不存在闭式解。
变分推断是变分法在推断问题的应用,通过寻找一个简单分布 𝑄(𝑧|𝑋)来近似后验概率分布 𝑃(𝑧|𝑋),当两者差距相对较小的时候,就可以将其作为近似估计,也称为贝叶斯变分。在衡量两个分布是否接近时,往往会选用 KL 散度(Kullback-Leibler Divergence, 𝐾𝐿),其定义如下:
D
K
L
[
Q
∥
P
]
=
∫
Q
(
x
)
l
o
g
Q
(
x
)
P
(
x
)
d
x
D_{KL}[Q\Vert P]=\int Q(x)log\frac{Q(x)}{P(x)}dx
DKL[Q∥P]=∫Q(x)logP(x)Q(x)dx
由于 𝐾𝐿是关于两个概率密度函数的函数,因而原推断过程是一个泛函优化问题,其推导如下:
D
K
L
[
Q
(
z
∣
X
)
∥
P
(
z
∣
X
)
]
=
∫
Q
(
z
∣
X
)
l
o
g
Q
(
z
∣
X
)
P
(
z
∣
X
)
d
z
=
∫
Q
(
z
∣
X
)
[
l
o
g
Q
(
z
∣
X
)
−
l
o
g
P
(
z
∣
X
)
]
d
z
=
∫
Q
(
z
∣
X
)
[
l
o
g
Q
(
z
∣
X
)
−
l
o
g
P
(
X
∣
z
)
P
(
z
)
P
(
X
)
]
d
z
D_{KL}[Q(z|X)\Vert P(z|X)]=\int Q(z|X)log\frac{Q(z|X)}{P(z|X)}dz=\int Q(z|X)[logQ(z|X)-log{P(z|X)}]dz=\int Q(z|X)[logQ(z|X)-log\frac{P(X|z)P(z)}{P(X)}]dz
DKL[Q(z∣X)∥P(z∣X)]=∫Q(z∣X)logP(z∣X)Q(z∣X)dz=∫Q(z∣X)[logQ(z∣X)−logP(z∣X)]dz=∫Q(z∣X)[logQ(z∣X)−logP(X)P(X∣z)P(z)]dz
其中,E 为期望。注意到 𝑃(𝑋) 并不依赖于隐变量 𝑧,因此可将其移出,经过整
理后可得:
l
o
g
P
(
x
)
−
D
K
L
[
Q
(
z
∣
X
)
∥
P
(
z
∣
X
)
]
=
E
z
Q
(
z
∣
X
)
[
l
o
g
P
(
X
∣
z
)
]
−
D
K
L
[
Q
(
z
∣
X
)
∥
P
(
z
)
]
logP(x)-D_{KL}[Q(z|X)\Vert P(z|X)]=E_{z~Q(z|X)}[logP(X|z)]-D_{KL}[Q(z|X) \Vert P(z)]
logP(x)−DKL[Q(z∣X)∥P(z∣X)]=Ez Q(z∣X)[logP(X∣z)]−DKL[Q(z∣X)∥P(z)]
由于 KL 散度是一个非负值,因此在 𝐾𝐿[𝑄 (𝑧| 𝑋) 𝑃(𝑧| 𝑋)] 值为零时取到证据下界 (Evidence Lower Bound, ELBO),即等式左边为观测变量概率密度的对数形式,右边为目标下界。
在观测数据 𝑋 给定的情况下,𝑝(𝑋) 为固定值,若要使 𝐷𝐾𝐿[𝑄 (𝑧| 𝑋) 𝑃(𝑧| 𝑋)]尽可能地小,则要最大化目标下界,因此,原优化问题可以转换为寻找一个简单分布来最大化证据下界。
从神经网络的角度来看,𝑄(𝑧|𝑋) 就是编码器网络,𝑧 是网络中间的隐藏层表示,𝑃(𝑋|𝑧) 则是解码器网络。图2 1展示了将两部分网络合并得到的变分自编码器架构,其中推断网络输入为 X,输出为近似后验分布 𝑄(𝑧|𝑋),由均值 𝜇 隐藏层和方差 𝜎 隐藏层表示;生成网络的输入为 z,输出为概率分布 𝑃(𝑋|𝑧)。
推断网络和生成网络的目标都为最大化证据下界 ELBO,因此,变分自编码
器的总目标函数为:
L
V
A
E
=
E
z
Q
(
z
∣
X
)
[
l
o
g
P
(
X
∣
z
)
]
−
D
K
L
[
Q
(
z
∣
X
)
∥
P
(
z
)
]
L_{VAE}=E_{z~Q(z|X)}[logP(X|z)]-D_{KL}[Q(z|X) \Vert P(z)]
LVAE=Ez Q(z∣X)[logP(X∣z)]−DKL[Q(z∣X)∥P(z)]
工作流程可以总结为:
- 从观测数据中抽样,经过编码器推断网络,近似后验分布的充分统计量;
- 从该后验分布中采样,得到随机变量,经解码器生成网络,重构数据样本;
- 优化总目标函数,包含最大化样本的对数似然和最小化 KL 散度,求解模
型参数; - 训练完毕后,将已知分布的测试样本输入生成网络,映射成目标分布的数
据样本。
在实际求解时,期望 E 依赖于推断网络的参数,但是随机变量 𝑧 采样自后验分布 𝑄(𝑧|𝑋),它们之间并非确定性关系,因此无法直接求解 𝑧 关于推断网络参数的导数。此时,可以通过重参数技巧来将它们之间随机性的采样过程转化为确定性的函数关系。























 1万+
1万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








