【代码随想录】【动态规划】背包问题 - 01背包

于 2024-05-12 13:19:51 发布
阅读量956 收藏 29
点赞数 28
分类专栏： 算法学习笔记 文章标签： 动态规划 算法 leetcode java
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/weixin_42904738/article/details/138451914
版权

01背包

模板：01背包问题

问题描述

背包最多能容纳的体积是 V V V。
现在有 n n n个物品，其中第 i i i个物品的体积为 v [ i ] v[i] v[i]、价值为 w [ i ] w[i] w[i]。
求这个背包至多能装多大价值的物品？

特点：每一个物品只有一个，每一个物品可以选择装入背包（1）或者不装入背包（0）

解法一：二维dp

dp[i][j]：将下标小于等于 i 的物品放入容量为 j 的背包中所能取得的最大价值

在计算dp[i][j]时：对于下标为 i 的物品进行讨论：

  • 如果放不下物品 i（当前背包容量小于物品 i 的体积，j < v[i]）：dp[i][j] = dp[i-1][j] ，即将下标小于等于 i-1 的物品放入容量为 j 的背包中所能取得的最大价值
  • 如果能放下物品 i（j >= v[i]）：
    • 有两种选择：
      • 不放入物品 i ：dp[i][j] = dp[i-1][j]
      • 放入物品 i ：dp[i][j] = w[i] + dp[i-1][j-v[i]]
    • 从二者中选择能取得的最大价值更大的一个：dp[i][j] = max{dp[i-1][j], w[i] + dp[i-1][j-v[i]]}

递推公式：
d p [ i ] [ j ] = { j < v [ i ] : d p [ i − 1 ] [ j ] j ≥ v [ i ] : max ⁡ ( d p [ i − 1 ] [ j ] , w [ i ] + d p [ i − 1 ] [ j − v [ i ] ] ) dp[i][j] = \left\{\begin{matrix} j < v[i]: & dp[i-1][j]\\ j \ge v[i]: & \max (dp[i-1][j], w[i] + dp[i-1][j-v[i]]) \end{matrix}\right. dp[i][j]={j<v[i]:j≥v[i]:​dp[i−1][j]max(dp[i−1][j],w[i]+dp[i−1][j−v[i]])​

计算顺序：
在计算dp[i][j]时可能会用到dp[i-1][0…j]位置的值，在计算dp[i][j]之前要保证这些位置的值已经计算过了。
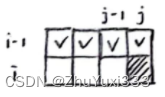
在这里插入图片描述
下面几种计算顺序都可以实现这一目标：

  • 外循环遍历物品，内循环遍历背包容量 / 一行一行计算
    • 每一行从左向右计算
    • 每一行从右向左计算
  • 外循环遍历背包容量，内循环遍历物品 / 一列一列计算
    • 每一列从上向下计算

在计算每一行时既可以按照从左向右的顺序计算，也可以按照从右向左的顺序计算，因为计算dp[i][j]时只会用到前一行的数据，不会用到本行该位置之前的数据（dp[i][0…j-1]）。

但是在计算每一列时必须按照从上向下的顺序计算，因为计算dp[i][j]时会用到本行该位置之前的数据（dp[i-1][j]）。

初始化：
不同的计算顺序需要初始化的内容有所不同：

  • 外循环遍历物品，内循环遍历背包容量 / 一行一行计算：只需要初始化第一行
  • 外循环遍历背包容量，内循环遍历物品 / 一列一列计算：既需要初始化第一行，又需要初始化第一列

具体来说：

  • 对第一行的初始化：i=0, j=0->V
    • dp[0][j]：在容量为j的背包中放物品0
      • j < v[0]：放不下，dp[0][j] = 0
      • j >= v[0]：能放下，dp[0][j] = w[0]
  • 对第一列的初始化：i=0->n-1, j=0
    • dp[i][0]：在容量为0的背包中放物品，dp[i][0] = 0

代码实现（计算顺序一）：

// 不用恰好装满的01背包 - 计算顺序1：外循环遍历物品，内循环遍历背包容量 / 一行一行计算
public int package01_1(){
    // dp[i][j]: 将下标小于等于 i 的物品放入容量为 j 的背包中所能取得的最大价值
    int[][] dp = new int[n][V+1];

    // 初始化第一行: dp[0][0...j]
    for(int j = 0; j <= V; j++){
        // dp[0][j]：在容量为j的背包中放物品0
        if(j < v[0]){
            dp[0][j] = 0; // 放不下物品0
        }else{
            dp[0][j] = w[0]; // 能放下物品0
        }
    }

    // 递推计算: 外循环遍历物品，内循环遍历背包容量
    for(int i = 1; i < n; i++){
        for(int j = 0; j <= V; j++){ // for(int j = V; j >= 0; j--)也可以
            if(j < v[i]){
                // 放不下物品i
                dp[i][j] = dp[i-1][j];
            }else{
                // 能放下物品i
                dp[i][j] = Math.max(
                    dp[i-1][j],             // 不放入物品i
                    w[i] + dp[i-1][j-v[i]]  // 放入物品i
                );
            }
        }
    }

    // 返回结果
    return dp[n-1][V];
}

代码实现（计算顺序二）：

// 不用恰好装满的01背包 - 计算顺序2：外循环遍历背包容量，内循环遍历物品 / 一列一列计算
public int package01_2(){
    // dp[i][j]: 将下标小于等于 i 的物品放入容量为 j 的背包中所能取得的最大价值
    int[][] dp = new int[n][V+1];

    // 初始化第一行: dp[0][0...j]
    for(int j = 0; j <= V; j++){
        // dp[0][j]：在容量为j的背包中放物品0
        if(j < v[0]){
            dp[0][j] = 0; // 放不下物品0
        }else{
            dp[0][j] = w[0]; // 能放下物品0
        }
    }
    // 初始化第一列: dp[0...n-1][0]
    for(int i = 0; i < n; i++){
        dp[i][0] = 0; // 在容量为0的背包中放物品
    }

    // 递推计算: 外循环遍历背包容量，内循环遍历物品
    for(int j = 1; j <= V; j++){
        for(int i = 1; i < n; i++){
            if(j < v[i]){
                // 放不下物品i
                dp[i][j] = dp[i-1][j];
            }else{
                // 能放下物品i
                dp[i][j] = Math.max(
                    dp[i-1][j],             // 不放入物品i
                    w[i] + dp[i-1][j-v[i]]  // 放入物品i
                );
            }
        }
    }

    // 返回结果
    return dp[n-1][V];
}

解法二：一维dp / 滚动数组

观察二维dp的递推公式发现：在计算dp[i][j]时只会用到前一行的数据，并且只会用到前一行的前j个数据。
d p [ i ] [ j ] = { j < v [ i ] : d p [ i − 1 ] [ j ] j ≥ v [ i ] : max ⁡ ( d p [ i − 1 ] [ j ] , w [ i ] + d p [ i − 1 ] [ j − v [ i ] ] ) dp[i][j] = \left\{\begin{matrix} j < v[i]: & dp[i-1][j]\\ j \ge v[i]: & \max (dp[i-1][j], w[i] + dp[i-1][j-v[i]]) \end{matrix}\right. dp[i][j]={j<v[i]:j≥v[i]:​dp[i−1][j]max(dp[i−1][j],w[i]+dp[i−1][j−v[i]])​

如果我们按照 “一行一行计算，每一行从右向左计算” 的顺序进行二维dp的计算：

...
在计算dp[i][j+1]时会用到dp[i-1][0], dp[i-1][1]...dp[i-1][j-1], dp[i-1][j], dp[i-1][j+1]
在计算dp[i][j]  时会用到dp[i-1][0], dp[i-1][1]...dp[i-1][j-1], dp[i-1][j]
在计算dp[i][j-1]时会用到dp[i-1][0], dp[i-1][1]...dp[i-1][j-1]
...

观察发现，在计算完dp[i][j]之后，就再也用不到dp[i-1][j]。

综上所述，我们可以只用一行（即一个长度为V+1的数组）作为dp数组，滚动存储每一行的计算结果，不再需要的数据被新计算的结果覆盖使用。

  • 一开始先将该数组的内容初始化为原二维dp的第一行的内容
  • 在计算原二维dp的第 i 行（ 2 ≤ i < n 2 \leq i < n 2≤i<n）时：
    • 计算开始前：滚动数组中正好是原二维dp第 i-1 行的内容
    • 从右向左计算（for(int j=V; j>=0; j--)）
    • 递推公式修改为： d p [ j ] = { j < v [ i ] : d p [ j ] j ≥ v [ i ] : max ⁡ ( d p [ j ] , w [ i ] + d p [ j − v [ i ] ] ) dp[j] = \left\{\begin{matrix} j < v[i]: & dp[j]\\ j \ge v[i]: & \max (dp[j], w[i] + dp[j-v[i]]) \end{matrix}\right. dp[j]={j<v[i]:j≥v[i]:​dp[j]max(dp[j],w[i]+dp[j−v[i]])​
    • 由递推公式计算出的 dp[j] 实际上就是原二维dp中的 dp[i][j]，而此时滚动数组中下标为 j 的位置存放的是 dp[i-1][j]，这个数值在之后的计算中都用不到了，因此将其覆盖用于存储 dp[i][j]。
public int package01(){
    // dp[j]: 向容量为 j 的背包中装物品所能取得的最大价值
    int[] dp = new int[V+1];

    // 初始化第一行: 在容量为j的背包中放物品0
    for(int j = 0; j <= V; j++){
        if(j < v[0]){
            dp[j] = 0; // 放不下物品0
        }else{
            dp[j] = w[0]; // 能放下物品0
        }
    }

    // 递推计算: 外循环遍历物品，内循环遍历背包容量
    for(int i = 1; i < n; i++){
        for(int j = V; j >= 0; j--){
            // if(j < v[i]){
            //     // 放不下物品i
            //     dp[j] = dp[j];
            // }else{
            //     // 能放下物品i
            //     dp[j] = Math.max(
            //         dp[j],             // 不放入物品i
            //         w[i] + dp[j-v[i]]  // 放入物品i
            //     );
            // }
            
            // 因为j < v[i]时其实不用有任何操作，所以简化为：
            if(j >= v[i]){
                dp[j] = Math.max(
                    dp[j],             // 不放入物品i
                    w[i] + dp[j-v[i]]  // 放入物品i
                );
            }
        }
    }

    // 返回结果
    return dp[V];
}

写好代码之后，再回过头来重新思考一维dp数组中每个状态的含义：

  • dp[j]: 向容量为 j 的背包中装物品所能取得的最大价值
  • 在计算dp[j]时，对每一个物品进行考察
    • 在对第 i 个物品的考察中：
      • 如果放不下第i个物品：dp[j] = dp[j]（什么也没做），放在二维dp中理解就是dp[i][j] = dp[i-1][j]
      • 如果能放下第i个物品，可以选择放入第 i 个物品，也可以选择不放入第 i 个物品，取最大值
    • 在遍历 i = 0 -> n-1 结束后，将本轮的全局最大值作为 dp[j] 的值

恰好装满的01背包

  • dp[j]: 恰好装满容量为 j 的背包，所能取得的最大价值。如果不能恰好装满，则等于 -1。
  • 在计算dp[j]时，对每一个物品进行考察：
    • 在对第 i 个物品的考察中：
      • 如果放不下第i个物品：dp[j] = dp[j]（什么也没做），放在二维dp中理解就是dp[i][j] = dp[i-1][j]
      • 如果能放下第i个物品，可以选择放入第 i 个物品，也可以选择不放入第 i 个物品，取最大值
        • 不放入第 i 个物品：dp[j] = dp[j]，放在二维dp中理解就是dp[i][j] = dp[i-1][j]
        • 放入第 i 个物品：
          • 如果从当前背包的容量 j 中减去第 i 个物品的容量后，剩下的容量（j-v[i]）不能恰好装满（dp[j-v[i]] == -1） ，那么放入第 i 个物品后也无法恰好装满：dp[j] = -1
          • 如果剩下的容量能够恰好装满，则：dp[j] = w[i] + dp[j-v[i]]
    • 在遍历 i = 0 -> n-1 结束后，将本轮的全局最大值作为 dp[j] 的值
  • 递推公式： d p [ j ] = { j < v [ i ] : d p [ j ] j ≥ v [ i ] : max ⁡ ( d p [ j ] , { j − v [ i ] = − 1 : d p [ j ] j − v [ i ] ≠ − 1 : w [ i ] + d p [ j − v [ i ] ] } ) dp[j] = \left\{\begin{matrix} j < v[i]: & dp[j]\\ j \ge v[i]: & \max (dp[j], \begin{Bmatrix} j-v[i] = -1: & dp[j]\\ j-v[i] \ne -1: & w[i] + dp[j-v[i]] \end{Bmatrix} ) \end{matrix}\right. dp[j]=⎩ ⎨ ⎧​j<v[i]:j≥v[i]:​dp[j]max(dp[j],{j−v[i]=−1:j−v[i]=−1:​dp[j]w[i]+dp[j−v[i]]​})​
public int package01_fillPerfect(){
    // dp[j]: 恰好装满容量为 j 的背包，所能取得的最大价值
    //        如果不能恰好装满，则等于 -1
    int[] dp = new int[V+1];
 
    // 初始化第一行: 在容量为j的背包中放物品0
    dp[0] = 0; // 在容量为0的背包中，什么也不放时认为是恰好装满
    for(int j = 1; j <= V; j++){
        if(j != v[0]){
            dp[j] = -1;    // 放不下物品0 and 能放下物品0但无法恰好装满
        }else{
            dp[j] = w[0];  // 恰好能放下物品0
        }
    }
 
    // 递推计算: 外循环遍历物品，内循环遍历背包容量
    for(int i = 1; i < n; i++){
        for(int j = V; j >= 0; j--){
            if(j >= v[i]){
                dp[j] = Math.max(
                    dp[j],                                     // 不放入物品i
                    dp[j-v[i]] == -1 ? -1 : w[i] + dp[j-v[i]]  // 放入物品i
                );
            }
        }
    }
 
    // 返回结果
    return dp[V] == -1 ? 0 : dp[V];
}

416. 分割等和子集

在这里插入图片描述在这里插入图片描述

代码实现：二维dp

class Solution {
    public boolean canPartition(int[] nums) {
        int n = nums.length;

        // 数组长度小于2时，不可能将数组分割成元素和相等的两个子集
        if(n < 2){
            return false;
        }

        // 计算整个数组的元素和sum、数组中最大元素maxNum
        int sum = 0;
        int maxNum = 0;
        for(int i = 0; i < n; i++){
            sum += nums[i];
            if(nums[i] > maxNum){
                maxNum = nums[i];
            }
        }

        // sum为奇数时，不可能将数组分割成元素和相等的两个子集
        if(sum % 2 == 1){
            return false;
        }

        int target = sum / 2; // 目标背包容量
        // System.out.println("target: " + target);

        // 当maxNum > target（即maxNum > sum/2）时，其余元素的元素和一定小于sum/2，不可能将数组分割成元素和相等的两个子集
        if(maxNum > target){
            return false;
        }

        // dp[i][j]: 从下标小于等于0的元素中选取元素，装入最大容量为j的背包中，能否恰好装满背包
        boolean[][] dp = new boolean[n][target+1];

        // 初始化：将下标为0的元素放入容量为j=0->target的背包中
        for(int j = 0; j <= target; j++){
            if(nums[0] == j){
                // 下标为0的元素恰好能装入容量为j的背包
                dp[0][j] = true;
            }else{
                dp[0][j] = false;
            }
            // System.out.println(0 + ", " + j + ": " + dp[0][j]);
        }

        // 递推计算
        for(int i = 1; i < n; i++){
            for(int j = 0; j <= target; j++){
                if(j < nums[i]){
                		// 装不下第i个元素
                    dp[i][j] = dp[i-1][j];
                }else{
                    // 能装下第i个元素
                    dp[i][j] = dp[i-1][j] || dp[i-1][j-nums[i]];
                }
                // System.out.println(i + ", " + j + ": " + dp[i][j]);
            }
        }

        // 返回结果
        return dp[n-1][target];
    }
}

代码实现：一维dp

class Solution {
    public boolean canPartition(int[] nums) {
        int n = nums.length;

        // 数组长度小于2时，不可能将数组分割成元素和相等的两个子集
        if(n < 2){
            return false;
        }

        // 计算整个数组的元素和sum、数组中最大元素maxNum
        int sum = 0;
        int maxNum = 0;
        for(int i = 0; i < n; i++){
            sum += nums[i];
            if(nums[i] > maxNum){
                maxNum = nums[i];
            }
        }

        // sum为奇数时，不可能将数组分割成元素和相等的两个子集
        if(sum % 2 == 1){
            return false;
        }

        int target = sum / 2; // 目标背包容量

        // 当maxNum > target（即maxNum > sum/2）时，其余元素的元素和一定小于sum/2，不可能将数组分割成元素和相等的两个子集
        if(maxNum > target){
            return false;
        }

        // dp[j]: 最大容量为j的背包能否恰好装满
        boolean[] dp = new boolean[target+1];

        // 初始化：将下标为0的元素放入容量为j=0->target的背包中
        for(int j = 0; j <= target; j++){
            if(nums[0] == j){
                // 下标为0的元素恰好能装入容量为j的背包
                dp[j] = true;
            }else{
                dp[j] = false;
            }
        }

        // 递推计算
        for(int i = 1; i < n; i++){
            for(int j = target; j >= 0; j--){
                // if(j < nums[i]){
                //     // 装不下第i个元素
                //     dp[j] = dp[j]; // 什么也没做
                // }else{
                //     // 能装下第i个元素
                //     dp[j] = dp[j] || dp[j-nums[i]];
                // }
                
                if(j >= nums[i]){
                    // 能装下第i个元素
                    dp[j] = dp[j] || dp[j-nums[i]];
                }
            }
        }

        // 返回结果
        return dp[target];
    }
}

1049. 最后一块石头的重量 Ⅱ

按照题目的定义：如果将stones分成两个子集，则最后一块石头的重量等于两个子集元素和的差值

因此，求 “最后一块石头的最小重量” 等价于 “使得两个子集的元素和的差值尽可能的小”

不妨设元素和较小的子集为子集A，元素和较大的子集为子集B，即 sum(子集A) <= totalSum/2 <= sum(子集B)

此时，问题进一步转换为 “使得子集A中元素和尽可能接近totalSum / 2”，即在保证子集A中元素和不超过totalSum/2的前提下，求子集A中元素和的最大值

进一步转换为01背包问题：

  • 有n个物品，每个物品只有一个，第i个物品的重量为stones[i]
  • 有一个最大容量为totalSum/2 = target的背包
  • 从这n个物品中选择若干个放入背包中，在保证不超过背包容量的前提下，求能放入的最大重量

通过背包问题求解出子集A中能放入的最大容量sum(子集A) = dp[n-1][target]后，计算最后一块石头的最小重量：sum(子集B) - sum(子集A) = (totalSum - sum(子集A)) - sum(子集A) = totalSum - 2*sum(子集A)

代码实现：二维dp

class Solution {
    public int lastStoneWeightII(int[] stones) {
        int n = stones.length;

        // 只有一块石头，不能进行粉碎操作，剩下的最小重量就是该石头的重量
        if(n < 2){
            return stones[0];
        }

        // 计算所有石头的总重量totalSum
        int totalSum = 0;
        for(int i = 0; i < n; i++){
            totalSum += stones[i];
        }
        
        int target = totalSum / 2;

        /*该问题可以转换为01背包问题：
        - 有n个物品，每个物品只有一个，第i个物品的重量为stones[i]
        - 有一个最大容量为totalSum/2的背包
        - 从这n个物品中选择若干个放入背包中，在保证不超过背包容量的前提下，求能放入的最大重量
        */

        // dp[i][j]：从下标小于等于i的物品中进行选择，放入最大容量为j的背包，能放入的最大重量
        int[][] dp = new int[n][target+1];

        // 初始化：向容量为j的背包中装物品0
        for(int j = 0; j <= target; j++){
            if(j < stones[0]){
                dp[0][j] = 0;         // 装不下物品0
            }else{
                dp[0][j] = stones[0]; // 能装下物品0
            }
        }

        // 递推计算
        for(int i = 1; i < n; i++){
            for(int j = 0; j <= target; j++){
                if(j < stones[i]){
                    // 装不下物品i
                    dp[i][j] = dp[i-1][j];
                }else{
                    // 能装下物品i
                    dp[i][j] = Math.max(
                        dp[i-1][j],                      // 选择1：不装入物品i
                        stones[i] + dp[i-1][j-stones[i]] // 选择2：装入物品i
                    );
                }
            }
        }

        // 返回结果
        // sum(子集A) = dp[n-1][target]
        // 最后一块石头的最小重量 = totalSum - 2*sum(子集A)
        return totalSum - 2 * dp[n-1][target];
    }
}

代码实现：一维dp
略

494. 目标和

该问题可以转换为01背包问题（如代码注释所述），需要注意的是在初始化的时候对背包容量为0时的情况的单独处理。

class Solution {
    public int findTargetSumWays(int[] nums, int target) {
        /* 将nums中的元素分成两个子集：加号集合、减号集合
         * 加号集合 - 减号集合 = target
         * 加号集合 + 减号集合 = totalSum
         * => 加号集合 = (target + sum)/2 = plusSum
         */

        int n = nums.length;

        int totalSum = 0; // 所有元素的元素和
        for(int i = 0; i < n; i++){
            totalSum += nums[i];
        }

        if((target + totalSum) % 2 != 0){
            return 0;
        }

        int plusSum = (target + totalSum) / 2; // 加号元素的元素和

        if(plusSum < 0){
            return 0;
        }

        /* 转换为01背包问题：
         * 共有n个物品，每个物品的重量是nums[i]，每个物品只有一个
         * 放入容量为plusSum的背包中
         * 将背包恰好装满的装法有多少种
         */

        // dp[i][j]: 从下标小于等于n的物品中进行选择，装入最大容量为j的背包中，将背包恰好装满的装法有多少种
        int[][] dp = new int[n][plusSum+1];

        // 初始化第一行：将下标为0的物品装入背包
        // 背包容量为0时：如果物品0重量不为0，则只有一种情况（什么也不装）；如果物品0重量为0，则有两种情况（装入物品0、什么也不装）
        dp[0][0] = (nums[0] == 0) ? 2 : 1;
        for(int j = 1; j <= plusSum; j++){
            if(nums[0] == j){
                // 物品0恰好装满背包
                dp[0][j] = 1;
            }else{
                dp[0][j] = 0;
            }
        }

        // 递推计算
        for(int i = 1; i < n; i++){
            for(int j = 0; j <= plusSum; j++){
                if(j < nums[i]){
                    // 装不下物品i
                    dp[i][j] = dp[i-1][j];
                }else{
                    // 能装下物品i
                    dp[i][j] = dp[i-1][j]          // 选择不装入物品i
                             + dp[i-1][j-nums[i]]; // 选择装入物品i
                }
            }
        }

        // 返回结果
        return dp[n-1][plusSum];
    }
}

474. 一和零

这道题可以看作是同时对体积和重量都有限制的01背包问题。

代码实现：三维dp

class Solution {
    public int findMaxForm(String[] strs, int m, int n) {
        int N = strs.length;

        // 统计每个字符串中0的个数（1的个数 = 该字符串的长度 - 0的个数）
        Map<String, Integer> map = new HashMap<>();
        for(int i = 0; i < N; i++){
            int zeroCnt = 0;
            for(int j = 0; j < strs[i].length(); j++){
                if(strs[i].charAt(j) == '0'){
                    zeroCnt++;
                }
            }
            map.put(strs[i], zeroCnt);
        }

        // dp[i][j][k]: 只从下标小于等于i的字符串中进行选择，装入最多有j个0和k个1的背包中，最多能装入的字符串个数
        int[][][] dp = new int[N][m+1][n+1];

        // 初始化第一行：在背包中装入物品0
        int zeroCnt = map.get(strs[0]);
        int oneCnt = strs[0].length() - zeroCnt;
        for(int j = 0; j <= m; j++){
            for(int k = 0; k <=n; k++){
                if(j < zeroCnt || k < oneCnt){
                    // 装不下物品0
                    dp[0][j][k] = 0;
                }else{
                    dp[0][j][k] = 1;
                }
            }
        }

        // 递推计算
        for(int i = 1; i < N; i++){
            for(int j = 0; j <= m; j++){
                for(int k = 0; k <= n; k++){
                    int curZeroCnt = map.get(strs[i]);
                    int curOneCnt = strs[i].length() - curZeroCnt;
                    if(j < curZeroCnt || k < curOneCnt){
                        // 装不下物品i
                        dp[i][j][k] = dp[i-1][j][k];
                    }else{
                        // 能装下物品i
                        dp[i][j][k] = Math.max(
                            dp[i-1][j][k], // 可以选择不装入物品i
                            1 + dp[i-1][j-curZeroCnt][k-curOneCnt] // 也可以选择装入物品i
                        );
                    }
                }
            }
        }

        // 返回结果
        return dp[N-1][m][n];
    }
}

优化：略

ZhuYuxi333
关注
  • 28
    点赞
  • 踩
  • 29
    收藏
    觉得还不错? 一键收藏
  • 0
    评论
专栏目录
代码随想录-大厂八股文-面试
04-25
代码随想录的大厂八股文面试相关知识点非常广泛，包括了编程基础、算法设计、代码组织、问题解决等多方面的知识点。为了通过面试，考察者需要具备扎实的编程基础和实践经验，能够熟练掌握多种编程语言和技术，能够写...
代码随想录-八股文 pdf
04-25
代码随想录-八股文 PDF 代码随想录-八股文 PDF 是一个涵盖了程序员学习必备的内容的知识星球精华，总结了包括 C++、Java、Go 在内的多种编程语言，数据结构和算法、操作系统、数据库、计算机网络、设计模式、Linux ...
【LeetCode刷题】动态规划实战——0-1背包问题（附Python代码）
D2Ooo的博客
07-26 1985
动态规划是一种用**空间**换**时间**的方法， 如果需要重复计算某个数，就把它记下来，以避免重复运算。
动态规划——01背包，完全背包，力扣题型讲解
weixin_43757333的博客
03-08 2097
本文带你解决力扣上所有典型的背包问题，通俗易懂的讲解。
动态规划（01背包问题）
会思想的苇草i的博客
10-07 3398
本文对动态规划的01背包问题进行了解释和阐述。
动态规划——01背包问题
Wu_L7的博客
04-22 3万+
面向小白的动态规划之01背包问题的详细讲解
动态规划——0/1背包问题(全网最细+图文解析)
Biteht的博客
05-08 6万+
01背包你真的掌握了吗?进来带你10分钟秒杀
【动态规划】01背包问题（滚动数组 + 手画图解）
这个人很勤快，但还是什么也没有。
02-11 5082
一、滚动数组的基本理解我对于滚动数组的理解是：滚动数组是基于二维数组之上产生的，之所以滚动数组能够用一维的方式去完成和二维同样的工作，原因就是在于这个滚动数组能够重复产生数据，进而有“滚动”的效果。滚动数组的本质还是二维数组，只是数据不再产生新的行，只在一行上一直进行数据的覆盖更新，因此要特别注意数据污染的情况。
代码随想录 动态规划、回溯、递归、二叉树、贪心
12-25
代码随想录全套文档 动态规划、回溯、递归、二叉树、贪心
00.代码随想录-最强八股文-第3版-无密版本.pdf
07-11
"代码随想录知识星球精华（最强八股文）第三版" 本资源摘要信息中，我们将根据给定的文件信息，生成相关知识点。 标题和描述中的知识点 * 代码随想录知识星球精华（最强八股文）第三版：这是一个关于编程的知识...
「代码随想录」动态规划专题精讲（v1.2）.pdf
07-15
「代码随想录」动态规划专题精讲（v1.2）.pdf
动态规划:01背包问题全解
m0_74846930的博客
08-24 954
/容量为target的背包最多能装多少价值的物品，价值就正好等于重量i<=target;i++){j--){
动态规划--01背包
qq_46844003的博客
12-21 636
动态规划--01背包篇
Leetcode—动态规划（背包问题）
最新发布
gxy的博客
10-21 314
类似于划分相等子集，尽量让石头分成重量相同的两堆，相撞之后剩下的石头最小，化解成01背包问题了。确定dp数组以及下标的含义：本题中每一个元素的数值既是重量，也是价值。dp[j]表示 背包总容量（所能装的总重量）是j，放进物品后，背的最大重量为dp[j]。本题中，石头的重量是 stones[i]，石头的价值也是 stones[i] ，可以 “最多可以装的价值为 dp[j]” == “最多可以背的重量为dp[j]”。
动态规划-（0-1）背包问题
菜鸟的博客
10-29 1万+
下面我用容积代表重量（我是不会承认我看走眼了的。又懒得改。）0-1背包问题是动态规划背包问题系列的最基础的一个问题。相对理解起来较为简单。按书上来说，要证明一个问题是否可以使用动态规划思想，需要满足最优子结构的性质，那么什么是最优子结构的性质呢？书上给出的定义如下图看起来很拗口，其实就是不论过去状态和决策如何，对前面的决策所形成的状态而言，余下的诸决策必须构成最优策略。说白了就是一个最优策略的子策略也是必须是最优的，而所有子问题的局部最优解将导致整个问题的全局最优。
动态规划之0-1背包问题（详解+分析+原码）
未见花闻的博客
05-08 4万+
本篇文章将介绍算法专题之动态规划中的背包问题，更准确的说是背包问题中最简单的一种类型，即0-1背包问题，就是给你一定容量的背包和若干物品，每种物品只能选一次，告诉你每件物品的价值和体积，求背包里面物品的最大总价值。
（一）、动态规划的基本思想
拉肚肚
04-21 1735
总结——01背包问题 （动态规划算法）
热门推荐
并非所有流浪者都迷失了自我
04-25 20万+
0-1 背包问题：给定 n 种物品和一个容量为 C 的背包，物品 i 的重量是 wi，其价值为 vi 。 问：应该如何选择装入背包的物品，使得装入背包中的物品的总价值最大？
代码随想录知识星球精华-大厂面试八股文v1.1.pdf
06-24
《代码随想录知识星球精华-大厂面试八股文v1.1.pdf》是一份介绍八股文的面试指南，针对大厂面试常见题型进行分类，以及给出相应的解答思路。这份资料具有很高的参考价值，在为即将面试的求职者提供指引的同时，也...

“相关推荐”对你有帮助么？

  • 非常没帮助
  • 没帮助
  • 一般
  • 有帮助
  • 非常有帮助
提交
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值