机器学习——决策树（分类）

前言：内容参考周志华老师的《机器学习》，确实是一本好书，不过本科生读懂还是有很大难度的，大多数模型都是直接给出公式，其实自己私下有推导，涉及好多自己不懂的数学知识，会一点点补充的

机器学习专栏：机器学习专栏

一、决策树基本流程

一颗决策树(decision tree)包括根节点、若干内部节点和若干叶子节点，不断的判断->分支->再判断->再分支……，决策树的构成其实是一个递归的过程，遵循分而治之的策略。

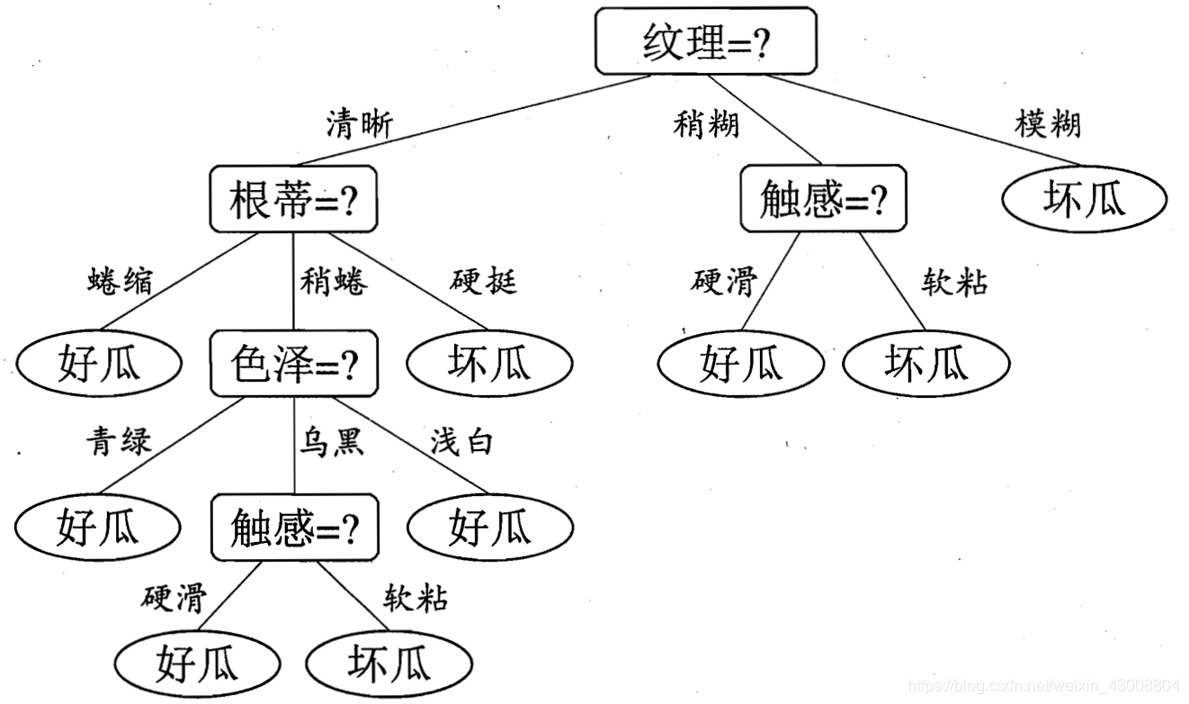
（图源：周志华老师的《机器学习》）

二、划分选择

决策树，最重要的当然是决策（或者说叫选择），那么根据什么标准进行选择呢？如何划分最优属性？我们希望决策树的分支结点所包含的样本尽可能属于同有类别，就是结点的“纯度”（purity）越来越高。

1、信息增益（ID3算法）

“信息熵”（information entropy）是度量样本集合纯度最常用的一种指标，信息熵的计算公式为：
$$Ent(D)=-\sum _{k=1}^K{p}_{k}lo{g}_2{p}_k$$
$Ent(D)$的值越小，则$D$的纯度越高。其中，$D$是总样本集，$p_k$表示第$k$类样本出现的概率（第$k$类样本占的比例），$K$是样本总类数。

“信息增益”（information gain）表示知道一个属性后，信息（标签判断）不确定性减少的程度，信息增益的计算公式为：
$$Gain(D,a)=Ent(D)-\sum _{v=1}^V\frac{|D^v|}{|D|}Ent(D^v)$$
其中，离散属性$a$有$N$种可能的取值$a^1,a^2,\dots ,a^V$，如果使用$a$对样本进行划分，则会产生$V$个分支结点，记$D^v$为$D$属性$a$上取值为$a^v$的样本集。
所以，“信息增益”越大，就意味着用属性$a$来划分数据集$D$来进行划分所获得的纯度提升越大。故著名的ID3决策树算法就是以信息增益来选择划分属性：
$$a^{\ast }=\underset{a\in A}{\mathrm{argmax}}Gain(D,a)$$

2、信息增益率（C4.5算法）

ID3决策树通过信息增益选取划分属性，观察信息增益的公式可以看出，如果属性$a$的属性值很多的情况下，一个属性值的分支节点的样本纯度就会很大，信息增益就会变大。所以C4.5决策算法采用“信息增益率”来选择划分属性。
“信息增益率”定义：
$$Gain\_ratio(D,a)=\frac{Gain(D,a)}{IV(a)}$$
其中
$$IV(a)=-\sum _{v=1}^V\frac{|D^v|}{|D|}lo{g}_2\frac{|D^v|}{|D|}$$
称为属性$a$的“固有值”（intrinsic value）。属性$a$的可能取值数目越多($V$越大)，则$IV(a)$的值通常会越大。
但是，“信息增益率”准则可能会对取值数目较少的属性有所偏好。所以，C4.5算法并不是直接选择“信息增益率”最大的候选划分属性，而是使用了一个启发式算法：

1. 先从候选划分属性中找出信息增益高于平均水平的属性；
2. 再从中选择信息增益率最高的。

3、基尼指数（CART算法）

CART决策树使用“基尼指数”（Gini index）来选择划分属性，数据集$D$的纯度用基尼指数来度量：
$$Gini(D)=\sum _{k=1}^K\sum _{k^{\prime }\ne k}{p}_k{p}_{k^{\prime }}$$
$Gini(D)$表示从$D$中随机抽取两个样本，其类别不一样的概率，故$Gini(D)$越小，$D$纯度越高。
对属性$a$的基尼指数定义为：
$$Gini\_index(D,a)=\sum _{v=1}^V\frac{D^v}{D}Gini(D^v)$$
因此，我们选择那个使划分后基尼指数最小的属性作为最优划分属性，即：
$$a^{\ast }=\underset{a\in A}{\mathrm{argmin}}Gini\_index(D,a)$$

三、剪枝处理

与线性回归一样，决策树也会存在过拟合的情况，线性回归的过拟合主要是通过正则化实现（可参考我的另一篇博客机器学习——特征缩放、正则化），决策树的过拟合主要是通过剪枝处理来避免的。

1、预剪枝

预剪枝是在决策树生成的过程中，对每个结点进行划分前先进行估计，若当前结点的划分不能带来决策树泛化性能（验证集的准确度）的提升，则停止划分将当前结点作为叶子结点（分类结果为该结点下占比大的类别）。

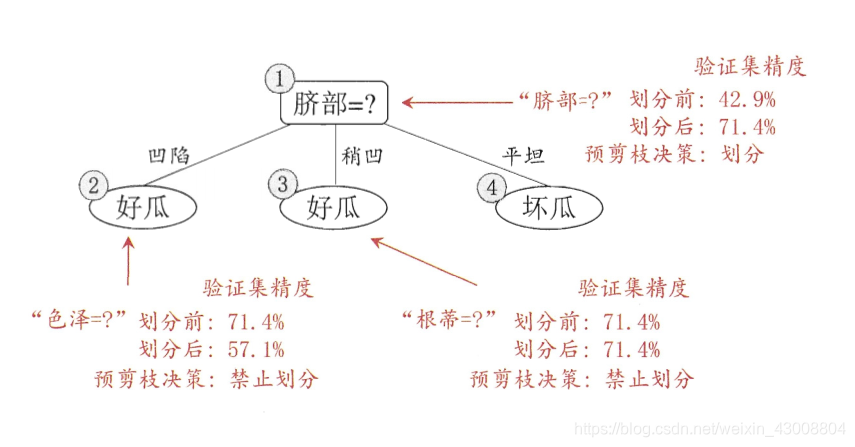
（图源：周志华老师的《机器学习》）

2、后剪枝

后剪枝是指先从训练集生成一颗完整的决策树，然后自下而上对非叶子结点进行考察，若将该结点及其子结点替换为叶子结点可以提高泛化能力（验证集的准确度），将该结点及其子结点替换为叶子结点（分类结果为该结点下占比大的类别）。

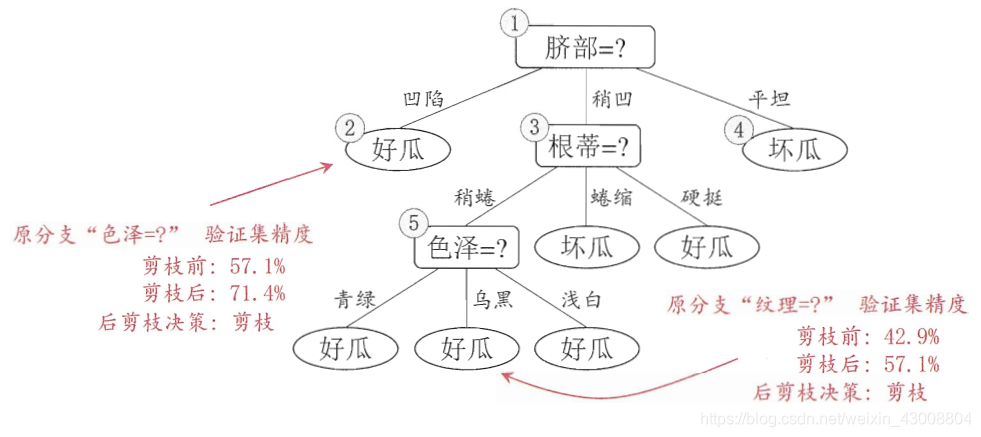
（图源：周志华老师的《机器学习》）

三、连续与缺失值处理

1、连续值处理

前面我们讨论的都是分类决策树，主要是通过离散属性来生成决策树，现实问题中，我们遇到的往往会有连续属性，这时我们就需要对连续值进行离散化处理，我们通常采用二分法（C4.5中采用的方法）

二分法：
给定样本集D和连续属性a，假定a在D中出现了n个不同的取值，将这些值从小到大进行排序，记为 { a 1 , a 2 , a 3 , . . . , a n } \{a^1,a^2,a^3,...,a^n\} {a1,a2,a3,...,an}。基于划分点$t$可以将D分为子集$D_t^{-}$和$D_t^{+}$，显然对于相邻的值$a^i和a^{i+1}$来说，$t$在区间$[a^i,a^{i+1})$中取任意值划分结果是一样的。因此，对于连续属性a，可能的侯划分点集合为：
$$T_a=\frac{a^i+a^{i+1}}{2}i\in [1,n-1]$$
二分法就体现在这，即把区间$[a^i,a^{i+1})$的中位点$\frac{a^i+a^{i+1}}{2}$作为侯划分点，我们要选取最优的划分点：
$$\begin{gathered} Gain(D,a)=\underset{t\in T_a}{\max }Gain(D,a,t) \\ Gain(D,a,t)=Ent(D)-\sum _{\lambda \in -,+}\frac{D_t^{\lambda }}{|D|}Ent(D_t^{\lambda }) \end{gathered}$$
其中，$Gain(D,a,t)$就是样本集D基于划分点t二分后的信息增益，我们就选择使$Gain(D,a,t)$最大化的划分点。

2、缺失值处理

存在缺失值我们主要有两个问题：

1. 如何在属性值缺失的情况下选择最优划分属性（如有的样本在“色泽”这个属性上的值是缺失的，那么该如何计算“色泽”的信息增益等？）；
2. 给定划分属性，若样本在该属性上缺失，如何对该样本进行划分（即这个样本到底属于哪一类？）。

对于问题1，现有数据集D和属性a，令$\tilde{D}$表示D在属性a上没有缺失值的样本子集，我们可以根据$\tilde{D}$来进行划分属性的选择。现假定属性a有V个值$a^1,a^2,...,a^V$，${\tilde{D}}^v$表示$\tilde{D}$中属性a取值为$a^v$的样本子集，${\tilde{D}}_k$表示$\tilde{D}$中属于第k类的样本子集。则有：
$$\{\begin{array}{c}\tilde{D}={\bigcup }_{k=1}^K{\tilde{D}}_k\\ \tilde{D}={\bigcup }_{v=1}^V{\tilde{D}}^v\end{array}$$
初始，我们为每一个样本$x$赋予一个权重$w_x$（初始化为1）,并定义：
$$\{\begin{array}{c}\rho =\frac{{\sum }_{x\in \tilde{D}}{w}_x}{{\sum }_{x\in D}{w}_x}\\ {\tilde{p}}_k=\frac{{\sum }_{x\in {\tilde{D}}_k}{w}_x}{{\sum }_{x\in \tilde{D}}{w}_x}\\ {\tilde{r}}_v=\frac{{\sum }_{x\in {\tilde{D}}^v}{w}_x}{{\sum }_{x\in \tilde{D}}{w}_x}\end{array}$$
其中，$\rho$表示无缺失值样本所占比例，${\tilde{p}}_k$表示无缺失值样本中第k类中所占比例，${\tilde{r}}_v$表示无缺失值样本中在属性a上取值为v的样本所占比例。显然：
$$\{\begin{array}{c}{\sum }_{k=1}^K{\tilde{p}}_k=1\\ {\sum }_{v=1}^V{\tilde{r}}_v=1\end{array}$$
基于上述定义，我们将含缺失值属性的信息增益计算推广为：
$$\begin{array}{rl}Gain(D,a)& =\rho \times Gain(\tilde{D},a)\\ & =\rho \times (Ent(\tilde{D})-\sum _{v=1}^V{\tilde{r}}_{v}Ent({\tilde{D}}^v))\end{array}$$
对问题2，若样本$x$在属性a上的取值未知，则将$x$划入所有子结点，权值由$w_x$变为$\tilde{r}\cdot w_x$，即让同一个样本以不同的概率划入不同的子结点中去。
这里推荐一篇博客，讲的很详细（包括实例计算过程）决策树（decision tree）（四）——缺失值处理

四、多变量决策树

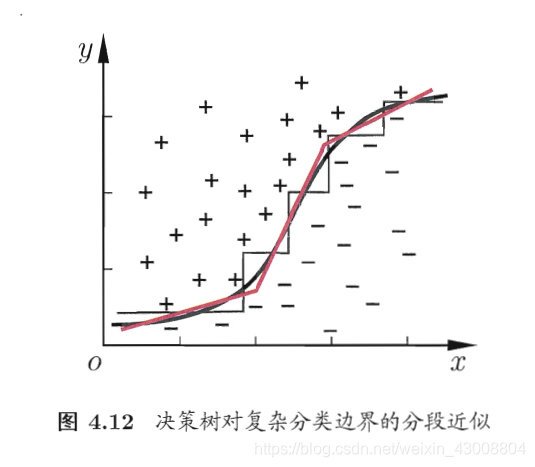
我们把每个属性视为坐标空间中的一个坐标轴，之前我们介绍的单变量决策树的分类边界都是与各个坐标轴平行的

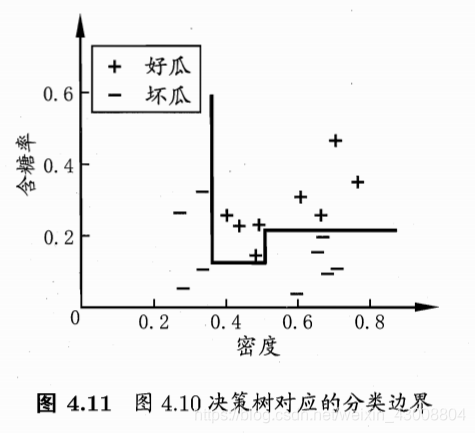
（图源：周志华老师的《机器学习》）

但是，当学习任务的真实边界比较复杂的时候，必须要使用很多段划分才能获得较好的近似，此时生成的决策树会很复杂。
此时，我们可能需要斜边去划分，“多变量决策树”（multivariate decision tree）的分叶子结点不再是针对某一个属性，而是一个线性分类器${\sum }_{i=1}^n{w}_i{a}_i=t$，其中$w_i$是属性$a_i$的权重，$w_i$和t可在该结点所含的样本集和属性值上学的。

五、sklearn实现决策树

可以看一看这一篇博文：DecisionTreeClassifier重要参数
这里再推荐一篇博文（分类结果的评价指标）：分类效果评估

# -*- coding: utf-8 -*-
"""
Created on Sun Nov 17 23:19:23 2019

@author: 1
"""

from sklearn import tree
import pydotplus
from IPython.display import Image
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score     # 准确率

df=pd.read_csv(r"D:\workspace\python\machine learning\data\iris.csv", sep=',')
iris_data=df.iloc[:, 0:3]
iris_target=df.iloc[:, 4]
iris_data_train, iris_data_test, iris_target_train,iris_target_test = train_test_split(iris_data,iris_target,train_size=.80)
clf = tree.DecisionTreeClassifier(criterion='gini')#criterion='gini'基尼指数，criterion='entropy'信息增益，
clf = clf.fit(iris_data_train, iris_target_train)  
dot_data = tree.export_graphviz(clf, out_file =None,
                         feature_names=df.columns[:3], # 特征名称
                         class_names=df.columns[4], # 目标变量的类别
                         filled=True, rounded=True,  
                         special_characters=True)  
y_pred=clf.predict(iris_data_test)
print('accuracy_score:',accuracy_score(iris_target_test, y_pred))
graph = pydotplus.graph_from_dot_data(dot_data)  
graph.write_png("out.png")     # 当前文件夹生成out.png

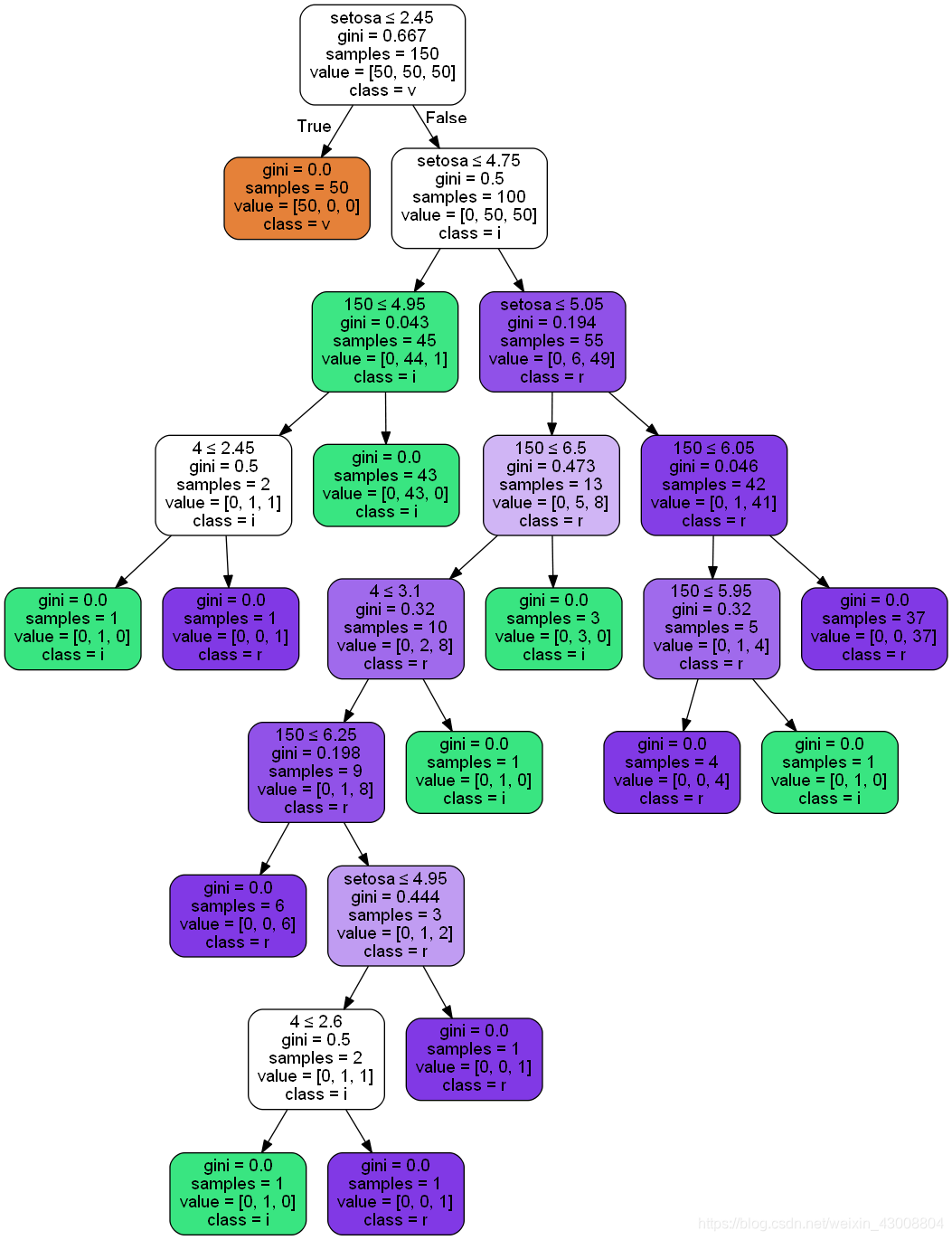
由iris数据集得到的决策树：