目录
1. Boosting 算法的思想

如上图,第一棵树的输出结果是Y1,第二棵树的输出是Y2,第三棵树的输出是Y3,而输入每次都是之前树的残差,具体课看下表:
| 编号t | 输入数据 X X X | 目标 Y Y Y | 输出数据 f t ( . ) = Y ^ f_t(.)=\hat{Y} ft(.)=Y^ |
|---|---|---|---|
| 1 | features | Y | Y1 |
| 2 | features | Y-Y1 | Y2 |
| 3 | features | Y-Y1-Y2 | Y3 |
因此,可以看出,boosting的方法是通过生长新的树不断减小之前树的残差
2. XGboost
通过阅读陈天奇的论文和PPT可以很容易理解xgb的目标函数
(1)
O
b
j
(
t
)
=
∑
i
=
1
n
l
(
y
i
,
y
^
i
(
t
)
)
+
∑
i
=
1
t
Ω
(
f
i
)
=
∑
i
=
1
n
l
(
y
i
,
y
^
i
(
t
−
1
)
+
f
t
(
x
i
)
)
+
Ω
(
f
t
)
+
constant
\begin{aligned} \begin{aligned} O b j^{(t)} &=\sum_{i=1}^{n} l\left(y_{i}, \hat{y}_{i}^{(t)}\right)+\sum_{i=1}^{t} \Omega\left(f_{i}\right) \\ &=\sum_{i=1}^{n} l\left(y_{i}, \hat{y}_{i}^{(t-1)}+f_{t}\left(x_{i}\right)\right)+\Omega\left(f_{t}\right)+\text { constant } \end{aligned}\tag{1} \end{aligned}
Obj(t)=i=1∑nl(yi,y^i(t))+i=1∑tΩ(fi)=i=1∑nl(yi,y^i(t−1)+ft(xi))+Ω(ft)+ constant (1)
该公式假设已经训练好前
t
−
1
t-1
t−1棵树,那么第
t
t
t棵树的输出就是
f
t
(
x
i
)
f_{t}\left(x_{i}\right)
ft(xi),那么这
t
t
t棵树与我们的目标值的残差可以表达为
∑
i
=
1
n
l
(
y
i
,
y
^
i
(
t
−
1
)
+
f
t
(
x
i
)
)
\sum_{i=1}^{n} l\left(y_{i}, \hat{y}_{i}^{(t-1)}+f_{t}\left(x_{i}\right)\right)
∑i=1nl(yi,y^i(t−1)+ft(xi)),其中
l
l
l是一个‘metrics’函数,但是需要注意的是,在下面的推倒中,需要保证
l
l
l二阶可导。
重要的思想,泰勒展开:
f
(
x
+
Δ
x
)
≃
f
(
x
)
+
f
′
(
x
)
Δ
x
+
1
2
f
′
′
(
x
)
Δ
x
2
f(x+\Delta x) \simeq f(x)+f^{\prime}(x) \Delta x+\frac{1}{2} f^{\prime \prime}(x) \Delta x^{2}
f(x+Δx)≃f(x)+f′(x)Δx+21f′′(x)Δx2。
我们已知
l
l
l二阶可导,那么公式(1)在
Δ
x
=
f
t
(
x
i
)
\Delta x=f_{t}\left(x_{i}\right)
Δx=ft(xi)处展开,可以表示为:
(2)
O
b
j
(
t
)
≃
∑
i
=
1
n
[
l
(
y
i
,
y
^
i
(
t
−
1
)
)
+
g
i
f
t
(
x
i
)
+
1
2
h
i
f
t
2
(
x
i
)
]
+
Ω
(
f
t
)
+
constant
\begin{aligned} O b j^{(t)} \simeq \sum_{i=1}^{n}\left[l\left(y_{i}, \hat{y}_{i}^{(t-1)}\right)+g_{i} f_{t}\left(x_{i}\right)+\frac{1}{2} h_{i} f_{t}^{2}\left(x_{i}\right)\right]+\Omega\left(f_{t}\right)+\text { constant }\tag{2} \end{aligned}
Obj(t)≃i=1∑n[l(yi,y^i(t−1))+gift(xi)+21hift2(xi)]+Ω(ft)+ constant (2)
其中定义:
g
i
=
∂
y
^
(
t
−
1
)
l
(
y
i
,
y
^
(
t
−
1
)
)
,
h
i
=
∂
y
^
(
t
−
1
)
2
l
(
y
i
,
y
^
(
t
−
1
)
)
g_{i}=\partial_{\hat{y}^{(t-1)}} l\left(y_{i}, \hat{y}^{(t-1)}\right), \quad h_{i}=\partial_{\hat{y}^{(t-1)}}^{2} l\left(y_{i}, \hat{y}^{(t-1)}\right)
gi=∂y^(t−1)l(yi,y^(t−1)),hi=∂y^(t−1)2l(yi,y^(t−1))
展开后我们得到一个有意思的结果,
l
(
y
i
,
y
^
i
(
t
−
1
)
)
l\left(y_{i}, \hat{y}_{i}^{(t-1)}\right)
l(yi,y^i(t−1))是一个常数项,因为我们已经假设前
t
−
1
t-1
t−1棵树已经训练好,那么公式(2)可以继续改写(常数项可以忽略不写)
(3)
O
b
j
(
t
)
=
∑
i
=
1
n
[
g
i
f
t
(
x
i
)
+
1
2
h
i
f
t
2
(
x
i
)
]
+
Ω
(
f
t
)
where
g
i
=
∂
y
^
(
t
−
1
)
l
(
y
i
,
y
^
(
t
−
1
)
)
,
h
i
=
∂
y
^
(
t
−
1
)
2
l
(
y
i
,
y
^
(
t
−
1
)
)
\begin{aligned} \begin{array}{l}{\quad O b j^{(t)} = \sum_{i=1}^{n}\left[g_{i} f_{t}\left(x_{i}\right)+\frac{1}{2} h_{i} f_{t}^{2}\left(x_{i}\right)\right]+\Omega\left(f_{t}\right)} \\ {\text { where } g_{i}=\partial_{\hat{y}^{(t-1)}} l\left(y_{i}, \hat{y}^{(t-1)}\right), \quad h_{i}=\partial_{\hat{y}^{(t-1)}}^{2} l\left(y_{i}, \hat{y}^{(t-1)}\right)}\end{array}\tag{3} \end{aligned}
Obj(t)=∑i=1n[gift(xi)+21hift2(xi)]+Ω(ft) where gi=∂y^(t−1)l(yi,y^(t−1)),hi=∂y^(t−1)2l(yi,y^(t−1))(3)
公式(3)中:g,h是很容易计算的,但
f
(
x
)
f(x)
f(x)如何去表示呢?因为它是一棵树,如何表示成函数的形式呢?
2.1. 重新定义一棵树
对于f的定义做一下细化,把树拆分成结构部分q和叶子权重部分w。下图是一个具体的例子。结构函数q把输入映射到叶子的索引号上面去,而w给定了每个索引号对应的叶子分数是什么。

2.2. 树的复杂度定义
定义这个复杂度包含了一棵树里面节点的个数,以及每个树叶子节点上面输出分数的L2模平方。当然这不是唯一的一种定义方式,不过这一定义方式学习出的树效果一般都比较不错。下图还给出了复杂度计算的一个例子。其中T是叶子结点的个数,w即为叶子权重

2.3. 回到目标函数
重新看一下目标函数
(4)
O
b
j
(
t
)
≃
∑
i
=
1
n
[
g
i
f
t
(
x
i
)
+
1
2
h
i
f
t
2
(
x
i
)
]
+
Ω
(
f
t
)
=
∑
i
=
1
n
[
g
i
w
q
(
x
i
)
+
1
2
h
i
w
q
(
x
i
)
2
]
+
γ
T
+
λ
1
2
∑
j
=
1
T
w
j
2
\begin{aligned} \begin{aligned} O b j^{(t)} & \simeq \sum_{i=1}^{n}\left[g_{i} f_{t}\left(x_{i}\right)+\frac{1}{2} h_{i} f_{t}^{2}\left(x_{i}\right)\right]+\Omega\left(f_{t}\right) \\ &=\sum_{i=1}^{n}\left[g_{i} w_{q\left(x_{i}\right)}+\frac{1}{2} h_{i} w_{q\left(x_{i}\right)}^{2}\right]+\gamma T+\lambda \frac{1}{2} \sum_{j=1}^{T} w_{j}^{2} \end{aligned}\tag{4} \end{aligned}
Obj(t)≃i=1∑n[gift(xi)+21hift2(xi)]+Ω(ft)=i=1∑n[giwq(xi)+21hiwq(xi)2]+γT+λ21j=1∑Twj2(4)
值得我们注意的是,对输入实例的遍历等价于对每个叶子结点实例的遍历,这里我们定义:
I
j
=
{
i
∣
q
(
x
i
)
=
j
}
I_{j}=\left\{i | q\left(x_{i}\right)=j\right\}
Ij={i∣q(xi)=j}。即
I
j
I_{j}
Ij为属于第
j
j
j个的结点的所有输入实例索引的集合,所以方程(4)可以改写为对叶子节点实例的遍历
(5)
O
b
j
(
t
)
≃
∑
i
=
1
n
[
g
i
f
t
(
x
i
)
+
1
2
h
i
f
t
2
(
x
i
)
]
+
Ω
(
f
t
)
=
∑
i
=
1
n
[
g
i
w
q
(
x
i
)
+
1
2
h
i
w
q
(
x
i
)
2
]
+
γ
T
+
λ
1
2
∑
j
=
1
T
w
j
2
=
∑
j
=
1
T
[
(
∑
i
∈
I
j
g
i
)
w
j
+
1
2
(
∑
i
∈
I
j
h
i
+
λ
)
w
j
2
]
+
γ
T
\begin{aligned} \begin{aligned} O b j ^ { ( t ) } & \simeq \sum _ { i = 1 } ^ { n } \left[ g _ { i } f _ { t } \left( x _ { i } \right) + \frac { 1 } { 2 } h _ { i } f _ { t } ^ { 2 } \left( x _ { i } \right) \right] + \Omega \left( f _ { t } \right) \\ & = \sum _ { i = 1 } ^ { n } \left[ g _ { i } w _ { q \left( x _ { i } \right) } + \frac { 1 } { 2 } h _ { i } w _ { q \left( x _ { i } \right) } ^ { 2 } \right] + \gamma T + \lambda \frac { 1 } { 2 } \sum _ { j = 1 } ^ { T } w _ { j } ^ { 2 } \\ & = \sum _ { j = 1 } ^ { T } \left[ \left( \sum _ { i \in I _ { j } } g _ { i } \right) w _ { j } + \frac { 1 } { 2 } \left( \sum _ { i \in I _ { j } } h _ { i } + \lambda \right) w _ { j } ^ { 2 } \right] + \gamma T \end{aligned}\tag{5} \end{aligned}
Obj(t)≃i=1∑n[gift(xi)+21hift2(xi)]+Ω(ft)=i=1∑n[giwq(xi)+21hiwq(xi)2]+γT+λ21j=1∑Twj2=j=1∑T⎣⎡⎝⎛i∈Ij∑gi⎠⎞wj+21⎝⎛i∈Ij∑hi+λ⎠⎞wj2⎦⎤+γT(5)
继续化简:令
G
j
=
∑
i
∈
I
j
g
i
H
j
=
∑
i
∈
I
j
h
i
G _ { j } = \sum _ { i \in I _ { j } } g _ { i } \quad H _ { j } = \sum _ { i \in I _ { j } } h _ { i }
Gj=∑i∈IjgiHj=∑i∈Ijhi,则:
(6)
O
b
j
(
t
)
=
∑
j
=
1
T
[
(
∑
i
∈
I
j
g
i
)
w
j
+
1
2
(
∑
i
∈
I
j
h
i
+
λ
)
w
j
2
]
+
γ
T
=
∑
j
=
1
T
[
G
j
w
j
+
1
2
(
H
j
+
λ
)
w
j
2
]
+
γ
T
\begin{aligned} \begin{aligned} O b j ^ { ( t ) } & = \sum _ { j = 1 } ^ { T } \left[ \left( \sum _ { i \in I _ { j } } g _ { i } \right) w _ { j } + \frac { 1 } { 2 } \left( \sum _ { i \in I _ { j } } h _ { i } + \lambda \right) w _ { j } ^ { 2 } \right] + \gamma T \\ & = \sum _ { j = 1 } ^ { T } \left[ G _ { j } w _ { j } + \frac { 1 } { 2 } \left( H _ { j } + \lambda \right) w _ { j } ^ { 2 } \right] + \gamma T \end{aligned}\tag{6} \end{aligned}
Obj(t)=j=1∑T⎣⎡⎝⎛i∈Ij∑gi⎠⎞wj+21⎝⎛i∈Ij∑hi+λ⎠⎞wj2⎦⎤+γT=j=1∑T[Gjwj+21(Hj+λ)wj2]+γT(6)
观察公式(6),中括号里是关于
w
j
w_j
wj的二次函数,直接求导或者利用中学时期的数学知识(
y
=
a
x
2
+
b
x
+
c
y=ax^2+bx+c
y=ax2+bx+c,在
x
=
−
b
/
2
a
x=-b/2a
x=−b/2a处取得极值)即可算出公式(6)的极值。
则公式(6)的极值点及极值为:
(7)
w
j
∗
=
−
G
j
H
j
+
λ
O
b
j
=
−
1
2
∑
j
=
1
T
G
j
2
H
j
+
λ
+
γ
T
\begin{aligned} w _ { j } ^ { * } = - \frac { G _ { j } } { H _ { j } + \lambda } \quad O b j = - \frac { 1 } { 2 } \sum _ { j = 1 } ^ { T } \frac { G _ { j } ^ { 2 } } { H _ { j } + \lambda } + \gamma T\tag{7} \end{aligned}
wj∗=−Hj+λGjObj=−21j=1∑THj+λGj2+γT(7)
2.4. 结构分数计算示例
Obj代表了当我们指定一个树的结构的时候,我们在目标上面最多减少多少。我们可以把它叫做结构分数(structure score)

但是问题来了,我们如何寻找树的形状?作者给了3种方法:
2.4.1. 暴力破解

2.4.2. 贪心算法
每一次尝试去对已有的叶子加入一个分割

对于每次扩展,我们还是要枚举所有可能的分割方案,如何高效地枚举所有的分割呢?我假设我们要枚举所有x < a 这样的条件,对于某个特定的分割a我们要计算a左边和右边的导数和。

我们可以发现对于所有的a,我们只要做一遍从左到右的扫描就可以枚举出所有分割的梯度和GL和GR。然后用上面的公式计算每个分割方案的分数就可以了。
观察这个目标函数,大家会发现第二个值得注意的事情就是引入分割不一定会使得情况变好,因为我们有一个引入新叶子的惩罚项。优化这个目标对应了树的剪枝, 当引入的分割带来的增益小于一个阀值的时候,我们可以剪掉这个分割。大家可以发现,当我们正式地推导目标的时候,像计算分数和剪枝这样的策略都会自然地出现,而不再是一种因为heuristic(启发式)而进行的操作了。
论文中对算法的描述(伪代码):

2.4.3. 近似算法
用于数据量很大,不能直接进行计算的情况:

2.5. 自定义损失函数 ,并计算一阶导 g i g_i gi和二阶导 h i h_i hi
2.5.1 Square loss
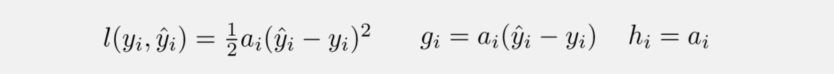
2.5.1 Logistic loss


参考
[1]. Chen T, Guestrin C. Xgboost: A scalable tree boosting system[C]//Proceedings of the 22nd acm sigkdd international conference on knowledge discovery and data mining. ACM, 2016: 785-794.
[2]. 陈天奇大神的PPT:https://homes.cs.washington.edu/~tqchen/pdf/BoostedTree.pdf
[3]. 贪心科技-机器学习特训营课程
[4]. xgboost原理(雪伦):https://blog.csdn.net/a819825294/article/details/51206410






















 323
323











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








