决策树系列(三)——基于决策树算法实现用户流失预测

基于决策树算法实现电信用户流失预测任务

任务描述：
  随着电信行业的不断发展，运营商们越来越重视如何扩大其客户群体。据研究，获取新客户所需的成本远高于保留现有客户的成本，因此为了满足在激烈竞争中的优势，保留现有客户成为一大挑战。对电信行业而言，可以通过数据挖掘等方式来分析可能影响客户决策的各种因素，以预测他们是否会产生流失（停用服务、转投其他运营商等）。

数据集：
  本案例所使用数据集来自Kaggle平台，可以从这里下载。数据集一共提供了7043条用户样本，每条样本包含21列属性，由多个维度的客户信息以及用户是否最终流失的标签组成，客户信息具体如下： 基本信息：包括性别、年龄、经济情况、入网时间等； 开通业务信息：包括是否开通电话业务、互联网业务、网络电视业务、技术支持业务等； 签署的合约信息：包括合同年限、付款方式、每月费用、总费用等。

一、引入工具包

import pandas as pd
import numpy as np

import matplotlib.pyplot as plt
import seaborn as sns

from sklearn.tree import DecisionTreeClassifier

from sklearn.model_selection import train_test_split
from sklearn.metrics import confusion_matrix
from imblearn.over_sampling import SMOTE

import graphviz
from sklearn import tree

二、数据加载

data = pd.read_csv('../data/WA_Fn-UseC_-Telco-Customer-Churn.csv')
pd.set_option('display.max_columns', None)
data.head()

特征含义：

变量名	描述	数据类型	取值
customerID	用户ID	string	7043个不重复值
gender	性别	string	Male，Female
SeniorCitizen	是否为老年人	int	0,1
Partner	是否有配偶	string	Yes，NO
Dependents	是否有家属	string	Yes，No
tenure	入网月数	int	0~72
PhoneService	是否开通电话业务	string	Yes，NO
MultipleLines	是否开通多线业务	string	Yes，No，No phone service
InternetService	是否开通互联网业务	string	DSL, Fiber optic, No
OnlineSecurity	是否开通在线安全业务	string	Yes，No,No internet service
OnlineBackup	是否开通在线备份业务	string	Yes，No,No internet service
DeviceProtection	是否开通设备保护业务	string	Yes，No,No internet service
TechSupport	是否开通技术支持业务	string	Yes，No,No internet service
StreamingTV	是否开通网络电视业务	string	Yes，No,No internet service
StreamingMovies	是否开通网络电影业务	string	Yes，NO，No internet service
Contract	合约期限	String	Month-to-Month，One Year，Two Year
PaperlessBilling	是否采用电子结算	string	YEs，NO
PaymentMethod	付款方式	string	check，Mailed check
MonthlyCharges	每月费用	float	18.25~118.75
TotalCharges	总费用	string	18.80~8684.80
Churn	客户是否流失	string	Yes，No

三、数据预处理

3.1 重复值处理

print("原数据集样本数量：{}".format(data.shape[0]))
print("数据集去重后样本数量：{}".format(data.drop_duplicates().shape[0]))

原数据集样本数量：7043
数据集去重后样本数量：7043

可以得出，该数据集无缺失值。

3.2 缺失值处理

missingDf = data.isnull().sum().sort_values(ascending=False).reset_index()
missingDf.columns = ['feature', 'missing_num']
missingDf['missing_percentage'] = missingDf['missing_num'] / data.shape[0]
missingDf.head()

  统计结果告诉我们数据集中应该没有缺失值，但是可能存在这样的情况：采用 ‘Null’、‘NaN’、’ ’ 等字符（串）表示缺失。数据集中就有这样一列TotalCharges特征，存在如下所示的11条样本，其特征值为空格字符（’ '）：

data[data['TotalCharges'] == ' ']

  对于TotalCharges这列原本为字符串类型的特征，由于其特征值含有数值意义，应该首先将其特征值转换为数值形式(浮点数)。此外，对其中不可转换的空格字符，可以用to_numeric()函数中的coerce参数将其转换为NaN。

# 将特征TotalCharges转为数值型
data['TotalCharges'] = pd.to_numeric(data['TotalCharges'],errors='coerce')

  一般我们常使用固定值(均值、中位数等)来进行数值型特征的缺失值填充，但通过观察缺失样本可知，tenure特征（表示客户的入网时间）均为0，，且在整个数据集中tenure为0与TotalCharges为缺失值是一一对应的。

  结合实际业务分析，这些样本对应的客户可能入网当月就流失了，但仍然要收取当月的费用，因此总费用即为该用户的每月费用（MonthlyCharges）。因此本案例最终采用MonthlyCharges的数值对TotalCharges进行填充。

# 使用MonthlyCharges填充TotalCharges
data['TotalCharges'] = data['TotalCharges'].fillna(data['MonthlyCharges']) 

3.3 异常值处理

1. 数值类特征

fig = plt.figure(figsize=(10,10))

# tenure
ax1 = fig.add_subplot(3,1,1)
sns.boxplot(data = data['tenure'],orient='h',ax=ax1).set(xlabel='tenure')

# MonthlyCharges
ax2 = fig.add_subplot(3,1,2)
sns.boxplot(data = data['MonthlyCharges'],orient='h',ax=ax2).set(xlabel='MonthlyCharges')

# TotalCharges
ax3 = fig.add_subplot(3,1,3)
sns.boxplot(data = data['TotalCharges'],orient='h',ax=ax3).set(xlabel='TotalCharges')

  由箱型图直观可见，这三列数值特征均不含离群点。同时，其他类别特征的取值也未见异常，因此不需要进行异常值处理。

四、特征选择

4.1 相关性分析

4.1 基本特征对客户流失影响

### 性别、是否老年人、是否有配偶、是否有家属等特征对客户流失的影响
baseCols = ['gender', 'SeniorCitizen', 'Partner', 'Dependents']

for i in baseCols:
    cnt = pd.crosstab(data[i], data['Churn'])    # 构建特征与目标变量的列联表
    cnt.plot.bar(stacked=True)    # 绘制堆叠条形图，便于观察不同特征值流失的占比情况
    plt.show()    # 展示图像

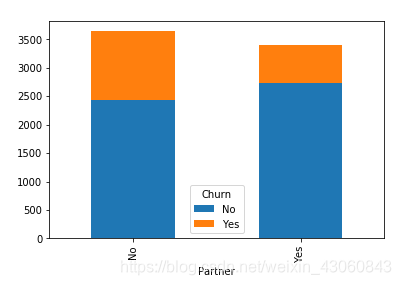
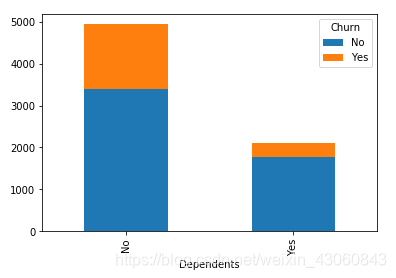
  由图可知：

• 性别对客户流失基本没有影响
• 年龄对客户流失有影响，老年人流失占比高于年轻人
• 是否有配偶对客户流失有影响，无配偶客户流失占比高于有配偶客户
• 是否有家属对客户流失有影响，无家属客户流失占比高于有家属客户

4.2 业务特征对客户流失影响

# 电话业务
posDf = data[data['PhoneService'] == 'Yes']
negDf = data[data['PhoneService'] == 'No']

fig = plt.figure(figsize=(10,4)) # 建立图像

ax1 = fig.add_subplot(121)
p1 = posDf['Churn'].value_counts()
ax1.pie(p1,labels=['No','Yes'],autopct='%1.2f%%',explode=(0,0.1))
ax1.set_title('Churn of (PhoneService = Yes)')

ax2 = fig.add_subplot(122)
p2 = negDf['Churn'].value_counts()
ax2.pie(p2,labels=['No','Yes'],autopct='%1.2f%%',explode=(0,0.1))
ax2.set_title('Churn of (PhoneService = No)')

plt.tight_layout(pad=0.5)    # 设置子图之间的间距
plt.show() # 展示饼状图

  由图可知，是否开通电话业务对客户流失影响较小。

# 多线业务
df1 = data[data['MultipleLines'] == 'Yes']
df2 = data[data['MultipleLines'] == 'No']
df3 = data[data['MultipleLines'] == 'No phone service']

fig = plt.figure(figsize=(15,4)) # 建立图像

ax1 = fig.add_subplot(131)
p1 = df1['Churn'].value_counts()
ax1.pie(p1,labels=['No','Yes'],autopct='%1.2f%%',explode=(0,0.1))
ax1.set_title('Churn of (MultipleLines = Yes)')

ax2 = fig.add_subplot(132)
p2 = df2['Churn'].value_counts()
ax2.pie(p2,labels=['No','Yes'],autopct='%1.2f%%',explode=(0,0.1))
ax2.set_title('Churn of (MultipleLines = No)')

ax3 = fig.add_subplot(133)
p3 = df3['Churn'].value_counts()
ax3.pie(p3,labels=['No','Yes'],autopct='%1.2f%%',explode=(0,0.1))
ax3.set_title('Churn of (MultipleLines = No phone service)')

plt.tight_layout(pad=0.5)    # 设置子图之间的间距
plt.show() # 展示饼状图

  由图可知，是否开通多线业务对客户流失影响很小。此外MultipleLines 取值为No和No phone service的两种情况基本一致，后续可以合并在一起。

# 互联网业务
cnt = pd.crosstab(data['InternetService'], data['Churn'])    # 构建特征与目标变量的列联表
cnt.plot.barh(stacked=True, figsize=(15,6))    # 绘制堆叠条形图，便于观察不同特征值流失的占比情况
plt.show()    # 展示图像 

  由图可知，未开通互联网的客户总数最少，而流失比例最低（7.40%）；开通光纤网络的客户总数最多，流失比例也最高（41.89%）；开通数字网络的客户则均居中（18.96%）。可以推测应该有更深层次的因素导致光纤用户流失更多客户，下一步观察与互联网相关的各项业务。

# 与互联网相关的业务
internetCols = ['OnlineSecurity', 'OnlineBackup', 'DeviceProtection', 'TechSupport', 'StreamingTV', 'StreamingMovies']

for i in internetCols:
    df1 = data[data[i] == 'Yes']
    df2 = data[data[i] == 'No']
    df3 = data[data[i] == 'No internet service']

    fig = plt.figure(figsize=(10,3)) # 建立图像
    plt.title(i)
    
    ax1 = fig.add_subplot(131)
    p1 = df1['Churn'].value_counts()
    ax1.pie(p1,labels=['No','Yes'],autopct='%1.2f%%',explode=(0,0.1))    # 开通业务

    ax2 = fig.add_subplot(132)
    p2 = df2['Churn'].value_counts()
    ax2.pie(p2,labels=['No','Yes'],autopct='%1.2f%%',explode=(0,0.1))    # 未开通业务

    ax3 = fig.add_subplot(133)
    p3 = df3['Churn'].value_counts()
    ax3.pie(p3,labels=['No','Yes'],autopct='%1.2f%%',explode=(0,0.1))    # 未开通互联网业务
  
    plt.tight_layout()    # 设置子图之间的间距
    plt.show() # 展示饼状图

  由图可知：所有互联网相关业务中未开通互联网的客户流失率均为7.40%，可以判断原因是上述六列特征均只在客户开通互联网业务之后才有实际意义，因而不会影响未开通互联网的客户；开通了这些新业务之后，用户的流失率会有不同程度的降低，可以认为多绑定业务有助于用户的留存；'StreamingTV’和 'StreamingMovies’两列特征对客户流失基本没有影响。此外，由于 ‘No internet service’ 也算是 ‘No’ 的一种情况，因此后续步骤中可以考虑将两种特征值进行合并。

4.2 合约特征对客户流失影响

# 合约期限
df1 = data[data['Contract'] == 'Month-to-month']
df2 = data[data['Contract'] == 'One year']
df3 = data[data['Contract'] == 'Two year']

fig = plt.figure(figsize=(15,4)) # 建立图像

ax1 = fig.add_subplot(131)
p1 = df1['Churn'].value_counts()
ax1.pie(p1,labels=['No','Yes'],autopct='%1.2f%%',explode=(0,0.1))
ax1.set_title('Churn of (Contract = Month-to-month)')

ax2 = fig.add_subplot(132)
p2 = df2['Churn'].value_counts()
ax2.pie(p2,labels=['No','Yes'],autopct='%1.2f%%',explode=(0,0.1))
ax2.set_title('Churn of (Contract = One year)')

ax3 = fig.add_subplot(133)
p3 = df3['Churn'].value_counts()
ax3.pie(p3,labels=['No','Yes'],autopct='%1.2f%%',explode=(0,0.1))
ax3.set_title('Churn of (Contract = Two year)')

plt.tight_layout(pad=0.5)    # 设置子图之间的间距
plt.show() # 展示饼状图

由图可知：合约期限越长，用户的流失率越低。

# 是否采用电子结算
df1 = data[data['PaperlessBilling'] == 'Yes']
df2 = data[data['PaperlessBilling'] == 'No']

fig = plt.figure(figsize=(10,4)) # 建立图像

ax1 = fig.add_subplot(121)
p1 = df1['Churn'].value_counts()
ax1.pie(p1,labels=['No','Yes'],autopct='%1.2f%%',explode=(0,0.1))
ax1.set_title('Churn of (PaperlessBilling = Yes)')

ax2 = fig.add_subplot(122)
p2 = df2['Churn'].value_counts()
ax2.pie(p2,labels=['No','Yes'],autopct='%1.2f%%',explode=(0,0.1))
ax2.set_title('Churn of (PaperlessBilling = No)')

plt.tight_layout(pad=0.5)    # 设置子图之间的间距
plt.show() # 展示饼状图

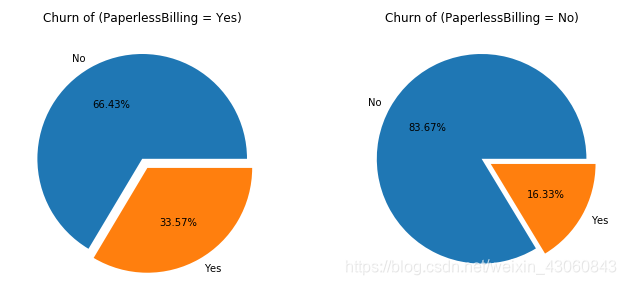
由图可知：采用电子结算的客户流失率较高，原因可能是电子结算多维按月支付的形式。

# 付款方式
df1 = data[data['PaymentMethod'] == 'Bank transfer (automatic)']    # 银行转账（自动）
df2 = data[data['PaymentMethod'] == 'Credit card (automatic)']    # 信用卡（自动）
df3 = data[data['PaymentMethod'] == 'Electronic check']    # 电子支票
df4 = data[data['PaymentMethod'] == 'Mailed check']    # 邮寄支票

fig = plt.figure(figsize=(10,8)) # 建立图像

ax1 = fig.add_subplot(221)
p1 = df1['Churn'].value_counts()
ax1.pie(p1,labels=['No','Yes'],autopct='%1.2f%%',explode=(0,0.1))
ax1.set_title('Churn of (PaymentMethod = Bank transfer')

ax2 = fig.add_subplot(222)
p2 = df2['Churn'].value_counts()
ax2.pie(p2,labels=['No','Yes'],autopct='%1.2f%%',explode=(0,0.1))
ax2.set_title('Churn of (PaymentMethod = Credit card)')

ax3 = fig.add_subplot(223)
p3 = df3['Churn'].value_counts()
ax3.pie(p3,labels=['No','Yes'],autopct='%1.2f%%',explode=(0,0.1))
ax3.set_title('Churn of (PaymentMethod = Electronic check)')

ax4 = fig.add_subplot(224)
p4 = df4['Churn'].value_counts()
ax4.pie(p4,labels=['No','Yes'],autopct='%1.2f%%',explode=(0,0.1))
ax4.set_title('Churn of (PaymentMethod = Mailed check)')

plt.tight_layout(pad=0.5)    # 设置子图之间的间距
plt.show() # 展示饼状图

  由图可知，四种付款方式中采用电子支票的客户流失率远高于其他三种。

五、特征工程

5.1 删除明显和预测值无关的特征

data.drop(['customerID', 'gender', 'PhoneService', 'StreamingTV', 'StreamingMovies'],inplace=True,axis=1)
data.shape

(7043, 16)

5.2 相关系数矩阵衡量连续型特征相关性

pearson_mat = data[['tenure', 'MonthlyCharges', 'TotalCharges']].corr(method='spearman')

plt.figure(figsize=(10,10))
ax = sns.heatmap(pearson_mat,square=True,annot=True,cmap='YlGnBu')
bottom, top = ax.get_ylim()
ax.set_ylim(bottom + 0.5, top - 0.5)
plt.show()

  由图可知，TotalCharges和tenure相关系数达到0.89，可以视作高度相关，因此可以删除该列，避免特征冗余。

data = data.drop(['TotalCharges'], axis=1)
data.shape

(7043, 15)

5.3 卡方检验衡量离散型特征相关性

待补充

5.4 特征标准化

NO 和 No internet service意义相同，将其合并

for fea in ['OnlineSecurity','OnlineBackup','DeviceProtection','TechSupport']:
    data.loc[data[fea] == 'No internet service',fea] = 'No'

NO 和 No phone service意义相同，将其合并

data.loc[data['MultipleLines'] == 'No phone service','MultipleLines'] = 'No'

将二分类变量转为数值型变量

for fea in ['Partner','Dependents','MultipleLines','OnlineSecurity','OnlineBackup','DeviceProtection','TechSupport',"PaperlessBilling",'Churn']:
    data[fea] = data[fea].apply(lambda x :1 if x == 'Yes' else 0)

将三分类变量转为数值型变量

for fea in  ['InternetService', 'Contract', 'PaymentMethod']:
    labels = data[fea].unique().tolist()
    data[fea] = data[fea].apply(lambda x:labels.index(x))

六、模型训练

6.1 切分特征和标签

X = data.iloc[:,0:-1]
y = data['Churn']

6.2 样本不均衡问题

y.value_counts()

0 5174
1 1869
Name: Churn, dtype: int64

由于样本量过少，使用上采样对样本进行补充

sm = SMOTE(random_state=20)
X, y = sm.fit_sample(X,y)

补充后的样本：

pd.Series(y).value_counts()

1 5174
0 5174
dtype: int64

6.3 切分训练集和测试集

X = pd.DataFrame(X)
y = pd.DataFrame(y)

X_train,X_test,Y_train,Y_test = train_test_split(X, y, test_size=0.3,random_state=0)
for i in [X_train,X_test,Y_train,Y_test]:
    i.index = range(i.shape[0])

6.4 模型训练

clf = DecisionTreeClassifier(random_state=0)
clf = clf.fit(X_train,Y_train)
score = clf.score(X_test,Y_test)
score

0.8109500805152979

6.5 模型评估

取精确率、召回率以及综合两者的F1值，但关注的重点仍然放在召回率上

# 导入精确率、召回率、F1值等评价指标
from sklearn.metrics import precision_score, recall_score, f1_score    

pred = clf.predict(X_test)

召回率:

r = recall_score(Y_test,pred)
r

0.8254172015404364

精确率：

p = precision_score(Y_test,pred)
p

0.8032479700187383

F1值：

f1 = f1_score(Y_test,pred)
f1

0.8141817030705919

七、模型优化

7.1 剪枝处理，绘制max_depth学习曲线

from sklearn.model_selection import cross_val_score
tr = []
te = []
for i in range(20):
    clf = DecisionTreeClassifier(random_state=0,max_depth=i+1,criterion='gini')
    clf = clf.fit(X_train,Y_train)
    score_tr = clf.score(X_train,Y_train)
    score_te = cross_val_score(clf,X,y,cv=10).mean()
    tr.append(score_tr)
    te.append(score_te)
    
plt.plot(range(1,21),tr,color='red',label='train')
plt.plot(range(1,21),te,color='blue',label='test')
plt.xticks(range(1,21))
plt.legend()
plt.show()

剪枝后最优深度：

te.index(max(te))

8

7.2 网格搜索，寻找最优参数

from sklearn.model_selection import GridSearchCV
gini_thresholds = np.linspace(0,0.5,20)

parameters = {
    'splitter':('best','random')
    ,'criterion':("gini","entropy")
    ,"max_depth":[*range(1,10)]
    ,'min_samples_leaf':[*range(1,50,5)]
    ,'min_impurity_decrease':[*np.linspace(0,0.5,20)]
}
clf = DecisionTreeClassifier(random_state=25)
GS = GridSearchCV(clf, parameters, cv=10)
GS.fit(X_train,Y_train)

最优参数:

GS.best_params_

{‘criterion’: ‘entropy’,
‘max_depth’: 9,
‘min_impurity_decrease’: 0.0,
‘min_samples_leaf’: 1,
‘splitter’: ‘best’}

GS.best_score_

0.8185881120213374

7.3 使用最优参数建立模型

clf = DecisionTreeClassifier(random_state=0,criterion='entropy',max_depth=9,min_impurity_decrease=0,min_samples_leaf=1,splitter='best')
clf = clf.fit(X_train,Y_train)
score = clf.score(X_test,Y_test)
score

pred = clf.predict(X_test)

召回率：

r = recall_score(Y_test,pred)
r

0.865211810012837

准确率：

p = precision_score(Y_test,pred)
p

0.7943429581614614

F1得分：

f1 = f1_score(Y_test,pred)
f1

0.8282642089093702