Djikstra算法原理、最优性证明及代码示例

去年参加项目使用了Djikstra算法，参考了网上博客和文章明白了算法流程，但是对于规划结果的最优性一直存在疑惑，最近梳理了一套自己的理解，和大家分享

0符号说明

• $\mathrm{P}(i\to j)$表示点$i$到点j的路径（P是Path的缩写），是路径，中间可能存在其他点；
• ${\mathrm{P}}_{\min }(i\to j)$表示$i$到$j$的最短路径；
• ${\mathrm{P}}_{\min \_\mathrm{c}}(i\to j)$表示在算法执行过程中$i$到$j$暂时的最短路径（c是current的缩写），还未确认，不一定是最短的，可能随着算法的运行找到更短的；
• $\mathrm{e}(i\to j)$表示$i$到$j$直连（e是edge的缩写），从点$i$直接到点$j$，中间没有中继点；
• “+”表示路径段拼接，例如${\mathrm{P}}_{\min }(i\to j)+\mathrm{e}(\mathrm{j}\to \mathrm{k})$表示从$i$到$j$的最短路径与点$i$到$j$的直连拼接；
• “A$\stackrel{\mathrm{P}}{=}$B”表示路径A和路径B相同；
• “A=B”表示路径A和路径B长度相等；
• “A≥B”表示路径A长度不小于路径B长度；
• “A≤B”表示路径A长度不大于路径B长度；
• “A>B”表示路径A长度大于路径B长度；
• “A<B”表示路径A长度小于路径B长度；

1算法流程

给定有向图$D$，可以查询给定两个点$i$和$j$之间的直连$\mathrm{e}(i\to j)$的距离$D(i,j)$,$D(i,j)=D(j,i)$，起点id为$s$，终点id为$t$。
1 ) 初始化：初始化close表和open表，close表为空，除了起点$s$之外的点共$m$个，将这些点都加入到open表中，记close表为$C$，open表为$O$;
2) 计算open表中所有点$i=1,\dots ,m$，与起点$s$的距离 ，记录每个点最新的最短距离$d_{\min \_c}^i$和对应的最新最短路径${\mathrm{P}}_{\min \_\mathrm{c}}^i={\mathrm{P}}_{\min \_\mathrm{c}}(s\to i)$中，对比$d_{\min \_c}^i$的取值，取其中最近距离的点$i{d}_{\min }$加入$C$，并将该点从$O$中删除
3) 循环执行以下步骤：
（1） 判断新加入的点$i{d}_{\min }$是否为终点$t$，如果是，则退出循环，如果不是，执行下一步;
（2） 以点$i{d}_{\min }$为中继点，对$O$中每个点$i$计算：起点$s$到点的最短路径${\mathrm{P}}_{\min }(s\to i{d}_{\min })$的距离+点$n$与点$i$直连$\mathrm{e}(i{d}_{\min }\to i)$的距离之和$d_{\mathrm{sum}}$，即$d_{\mathrm{sum}}={\mathrm{P}}_{\min }(s\to n)+\mathrm{e}(n\to i)$
（3） 判断$d_{\mathrm{sum}}$是否比目前$i$的最短距离$d_{\min \_c}^i$小，如果是，则
$$d_{\min \_c}^i=d_{\mathrm{sum}}$$

$${\mathrm{P}}_{\min \_\mathrm{c}}^i\stackrel{\mathrm{P}}{=}{\mathrm{P}}_{\min }(s\to i{d}_{\min })+\mathrm{e}(i{d}_{\min }\to i)$$，继续执行以下步骤
（4） 对$O$中所有点$i$，对比$d_{\min \_\mathrm{c}}^i$的取值，将其中取值最小的点$i{d}_{\min }$加入 ，并从$O$中删除，并执行

$${\mathrm{P}}_{\min }(s\to i{d}_{\min })\stackrel{\mathrm{P}}{=}{\mathrm{P}}_{\min \_\mathrm{c}}^{i{d}_{\min }}$$
即认为找到了$i{d}_{\min }$的最短路径

2最优性证明

思路：只需要证明每一次确认加入到close表中的点已经找到真正的最短路径，没有其他更短的路径可选，即可。
在前面的算法流程中有两步确认了最短路径：一个是步骤2），一个是步骤3）中的（3）

2.1步骤2）确认的第一个点路径最优性

假设存在其他路径${\mathrm{P}}_{\mathrm{other}}$更短，则该路径一定是经过某个点中继的，即存在$j\in O$使得
$${\mathrm{P}}_{\mathrm{other}}\stackrel{\mathrm{P}}{=}{\mathrm{P}}_{\min }(s\to j)+\mathrm{e}(j\to i{d}_{\min })$$
其中，${\mathrm{P}}_{\min }(s\to j)$表示$s$到点$j$的最短路径，$\mathrm{e}(j\to i{d}_{\min })$为点$j$到$i{d}_{\min }$直连。
可知存在一个点$k\in O$(可以是$j$），使得
$${\mathrm{P}}_{\min }(s\to j)\stackrel{\mathrm{P}}{=}\mathrm{e}(s\to k)+{\mathrm{P}}_{\min }(\mathrm{k}\to j)$$
其中，$\mathrm{e}(s\to k)$为$s$到点$k$直连，${\mathrm{P}}_{\min }(k\to j)$为点$k$到点$j$的最短路径
从而
$${\mathrm{P}}_{\mathrm{other}}\stackrel{\mathrm{P}}{=}\mathrm{e}(s\to k)+{\mathrm{P}}_{\min }(k\to j)+\mathrm{e}(j\to i{d}_{\min })$$
而根据步骤2)中操作可知，$i{d}_{\min }$是与$s$直连距离最短的，即
$$\mathrm{e}(s\to k)\ge \mathrm{e}(s\to i{d}_{\min })$$
而${\mathrm{P}}_{\min }(\mathrm{k}\to j)$和$\mathrm{e}(j\to i{d}_{\min })$的距离不小于0，即
$${\mathrm{P}}_{\min }(\mathrm{k}\to j)\ge 0$$
$$\mathrm{e}(j\to i{d}_{\min })\ge 0$$
因此
$$\mathrm{e}(s\to k)+{\mathrm{P}}_{\min }(k\to j)+\mathrm{e}(j\to i{d}_{\min })\ge \mathrm{e}(s\to i{d}_{\min })$$
因此路径${\mathrm{P}}_{\mathrm{other}}$的距离一定不小于$\mathrm{e}(s\to i{d}_{\min })$的距离，即对于点$i{d}_{\min }$不存在比直连更短的路径。

备注：${\mathrm{P}}_{\min }(k\to j)$和$\mathrm{e}(j\to i{d}_{\min })$两段路径距离必须不小于0，这样相加后才能使上面的逻辑成立，这也是为什么Djikstra算法不能用于负权值的路径规划问题，如果存在负权重，则其他可行路径加上负权重后可能比当前最短权重更小！

2.2步骤3).(3)确认点的路径最优性

经过步骤3)中的（4）更新，可知对$\forall i\in C$，即经$C$中的点中转的路径必然比目前记录的最短路径更长，即
$${\mathrm{P}}_{\min }(s\to i)+\mathrm{e}(i\to i{d}_{\min })\ge {\mathrm{P}}_{\min \_c}(s\to i{d}_{\min })\text{\hspace{1em}(1.1)}$$
如果还存在其他更短的路径，只能是经过$O$中的点中转，即$\exists k\in O$，使得
$${\mathrm{P}}_{\min }(s\to k)+\mathrm{e}(\mathrm{k}\to i{d}_{\min })<{\mathrm{P}}_{\min \_c}(s\to i{d}_{\min })\text{\hspace{1em}(1.2)}$$
从直观的感觉上，$i{d}_{\min }$是$O$中路径最短的，其他点$k$的最短路径应该是比$i{d}_{\min }$要更长的，即
$${\mathrm{P}}_{\min }(s\to k)\ge {\mathrm{P}}_{\min \_c}(s\to i{d}_{\min })\text{\hspace{1em}(1.3)}$$
如果这个关系成立，那么在$\mathrm{e}(\mathrm{k}\to i{d}_{\min })\ge 0$的前提下，式(1.2)也就不成立。所以下面证明式(1.3)。

2.2.1证式(1.3)

反证法：假设$\exists k\in O$使得
$${\mathrm{P}}_{\min }(s\to k)<{\mathrm{P}}_{\min \_\mathrm{c}}(s\to i{d}_{\min })\text{\hspace{1em}(1.4)}$$
考虑起点$s$到$k$的最短路径可能的三种情况

• A.直连

即
$${\mathrm{P}}_{\min }(s\to k)\stackrel{\mathrm{P}}{=}\mathrm{e}(s\to k)\text{\hspace{1em}(1.5)}$$
在步骤2)中就已经将这一最短路径更新到了${\mathrm{P}}_{\min \_\mathrm{c}}^k=\mathrm{e}(s\to k)$中，根据假设这是到$k$的最短路径，那么后续每一次循环更新都未改变，因此在步骤（4）中仍有
$${\mathrm{P}}_{\min \_\mathrm{c}}^k=\mathrm{e}(s\to k)\stackrel{\mathrm{P}}{=}{\mathrm{P}}_{\min }(s\to k)\text{\hspace{1em}(1.6)}$$
根据式(1.4)有
$${\mathrm{P}}_{\min \_\mathrm{c}}^k<{\mathrm{P}}_{\min \_\mathrm{c}}(s\to i{d}_{\min })\text{\hspace{1em}(1.7)}$$
那么在$k$才是（4）中距离最小的点，不是$i{d}_{\min }$，矛盾，排除这种情况。

• B. 经过目前在$C$中的点中转

$\exists r\in C$，使得
$${\mathrm{P}}_{\min }(s\to k)\stackrel{\mathrm{P}}{=}{\mathrm{P}}_{\min }(s\to t)+\mathrm{e}(t\to k)\text{\hspace{1em}(1.8)}$$
根据式(1.4)有
$${\mathrm{P}}_{\min }(s\to t)+\mathrm{e}(t\to k)<{\mathrm{P}}_{\min \_\mathrm{c}}(s\to i{d}_{\min })\text{\hspace{1em}(1.9)}$$
根据第（4）步的更新过程可知，对$\forall t\in C$
$${\mathrm{P}}_{\min }(s\to t)+\mathrm{e}(t\to k)\ge {\mathrm{P}}_{\min \_\mathrm{c}}(s\to k)\text{\hspace{1em}(1.10)}$$
结合式(1.9)得到
$${\mathrm{P}}_{\min \_\mathrm{c}}(s\to k)<{\mathrm{P}}_{\min \_\mathrm{c}}(s\to i{d}_{\min })\text{\hspace{1em}(1.11)}$$
可见基于假设(1.4)，在执行步骤（4）时，$k$才是目前最短路径最小的，而不是$i{d}_{\min }$，矛盾，排除此情况

• C. 经过目前还在$O$中的点中转

$\exists r\in O,r\ne k$ ，使得
$${\mathrm{P}}_{\min }(s\to k)\stackrel{\mathrm{P}}{=}{\mathrm{P}}_{\min }(s\to r)+\mathrm{e}(r\to k)\text{\hspace{1em}(1.12)}$$
根据假设(1.4)有
$${\mathrm{P}}_{\min }(s\to r)+\mathrm{e}(r\to k)<{\mathrm{P}}_{\min \_\mathrm{c}}(s\to i{d}_{\min })\text{\hspace{1em}(1.13)}$$
其中$\mathrm{e}(r\to k)\ge 0$，因此
$${\mathrm{P}}_{\min }(s\to r)<{\mathrm{P}}_{\min \_\mathrm{c}}(s\to i{d}_{\min })\text{\hspace{1em}(1.14)}$$
这样问题又回到式(1.4)相同的表述：$\exists r\in C$使得
$${\mathrm{P}}_{\min }(s\to r)<{\mathrm{P}}_{\min \_\mathrm{c}}(r\to i{d}_{\min })\text{\hspace{1em}(1.15)}$$
只是多了一个条件$r\ne k$，继续按前面的方法考虑三种情况，又会回到相同的结论。即如果假设(1.4)成立，就要求$O$中有一个不同的点也满足(1.4)，这样(1.4)要成立就需要不断的使这个这“假设链”无限延长下去。
$$\exists k\to \exists r_1\to \exists r_2\to ...\text{\hspace{1em}(1.16)}$$
那么问题来了，如果我们能确保每次排除的点都不相同，也就是不能咬尾，不能在几个点上一直循环下去，这样在$O$不是无限集的情况下，就肯定会在某一步，集合$O$中所有点均被加入假设链，也就不存在一个点使前面的一连串假设成立，这样假设链崩塌，递归返回，假设(1.4)也就不成立。下面来证明“每次排除的点都不相同”

同样采用反证法：假设$\exists m<n,m,n\in N^{+}$，满足$r_n=r_m$，根据前面的推导有
$${\mathrm{P}}_{\min }(s\to r_m)\stackrel{\mathrm{P}}{=}{\mathrm{P}}_{\min }(r\to r_n)+\mathrm{e}(r_n\to r_{n-1})+\mathrm{e}(r_{n-1}\to r_{n-2})+...\mathrm{e}(r_{m+1}\to r_m)\text{\hspace{1em}(1.17)}$$
由于${\mathrm{P}}_{\min }(s\to r_m)={\mathrm{P}}_{\min }(r\to r_n)$，因此
$$\mathrm{e}(r_n\to r_{n-1})+\mathrm{e}(r_{n-1}\to r_{n-2})+...\mathrm{e}(r_{m+1}\to r_m)=0\text{\hspace{1em}(1.18)}$$
如果有向图的每条边均大于零，式(1.17)必然不成立，从而式(1.6)中的假设错误，不存在满足条件$m$和$n$，即每次加入假设链的点均不同，必然有$O$中的点被穷举完的时候。

那么再思考一下，如果每条边不一定大于零呢？这种情况的含义是：点$r_i,i=m,m+1,...,n$这几点之间是互通的，这几个点可以看作同一个点，他们内部之间可以通过
$$\mathrm{e}(r_n\to r_{n-1}),\mathrm{e}(r_{n-1}\to r_{n-2}),...\mathrm{e}(r_{m+1}\to r_m)$$

这些权重为0的直连“左脚踩右脚”绕来绕去，均不会改变其路径大小。但是无论饶多少圈，这样一个点群都需要与点群外的点相连形成到起点$s$的最短路径，其实这个时候这个点群和一个点没有区别，也需要继续找点群外的点，使式(1.16)的“假设链”延伸下去，因此也必然有$O$中的点被穷举完的时候。击鼓传花，最终将不存在$r_f\in C$使得
$${\mathrm{P}}_{\min }(s\to r_f)<{\mathrm{P}}_{\min \_c}(r_f\to i{d}_{\min })\text{\hspace{1em}(1.19)}$$
这样也就不存在$r_{f-1}\in C$使得
$${\mathrm{P}}_{\min }(s\to r_{f-1})<{\mathrm{P}}_{\min \_c}(r_{f-1}\to i{d}_{\min })\text{\hspace{1em}(1.20)}$$
….这样递归返回，不存在$r\in O,r\ne k$，使得
$${\mathrm{P}}_{\min }(s\to k)\stackrel{\mathrm{P}}{=}{\mathrm{P}}_{\min }(s\to r)+\mathrm{e}(r\to k)\text{\hspace{1em}(1.21)}$$
也就不存在$k\in O$使得
$${\mathrm{P}}_{\min }(s\to k)<{\mathrm{P}}_{\min \_\mathrm{c}}(s\to i{d}_{\min })\text{\hspace{1em}(1.22)}$$
即对$\forall k\in O$
$${\mathrm{P}}_{\min }(s\to k)\ge {\mathrm{P}}_{\min \_\mathrm{c}}(s\to i{d}_{\min })\text{\hspace{1em}(1.23)}$$
从而对$\forall k\in O$
$${\mathrm{P}}_{\min }(s\to k)+\mathrm{e}(\mathrm{k}\to i{d}_{\min })\ge {\mathrm{P}}_{\min \_\mathrm{c}}(s\to i{d}_{\min })\text{\hspace{1em}(1.24)}$$
即经过$O$中的点中转到$i{d}_{\min }$的路径不可能比${\mathrm{P}}_{\min \_\mathrm{c}}(s\to i{d}_{\min })$更短，证明完毕。

3应用示例

下面以地铁规划为例实践Djikstra算法

3.1程序

参考：https://blog.csdn.net/pythonlaodi/article/details/110431654中博主的代码，通过百度地图api获取成都地铁的站点信息。

获取地铁站点信息后，根据线路连接情况以及站点之间的直线距离构建前述有向图$D$

代码下载：链接:https://caiyun.139.com/m/i?0n5C9qHgSTp6B 提取码:DLzk

其中路网信息获取和作图用python实现，因为路径规划部分的程序之前用C++写的，不想再用python写一遍，就封装成了动态库给python调用

在完成创作后发现也有其他博主做了地铁规划的工作，都是用python实现的，不用像我这样每次规划部分的功能修改又要重新生成动态库，需要的同学也可以参考，例如:https://blog.csdn.net/qq_44874645/article/details/115913516。

下面是我的python部分的代码，其中地铁站点获取参考了前述链接https://blog.csdn.net/pythonlaodi/article/details/110431654

import requests
import numpy as np
import math
import re
import pandas as pd
import time
import matplotlib.pyplot as plt

import ctypes

# 加载动态库
lib = ctypes.CDLL("TestBH.dll", winmode=0)
# lib = ctypes.windll.LoadLibrary("TestBH.dll")  # 导入dll

#动态库输入参数设置
lib.Plan.argtypes=[ctypes.POINTER(ctypes.c_double * 2),ctypes.POINTER(ctypes.c_double * 2),
                   ctypes.POINTER(ctypes.c_double * 100),ctypes.POINTER(ctypes.c_double * 100),
                   ctypes.POINTER(ctypes.c_int * 100)]
#动态库返回参数设置
lib.Plan.restype=ctypes.c_int


PI = math.pi

null = None
#城市代码
city_code = 75
station_info = requests.get('http://map.baidu.com/?qt=bsi&c=%s&t=%s' % (
    city_code,
    int(time.time() * 1000)
))


station_info_json = eval(station_info.content)

def _transformlat(coordinates):
    lng = coordinates[:, 0] - 105
    lat = coordinates[:, 1] - 35
    ret = -100 + 2 * lng + 3 * lat + 0.2 * lat * lat + \
          0.1 * lng * lat + 0.2 * np.sqrt(np.fabs(lng))
    ret += (20 * np.sin(6 * lng * PI) + 20 *
            np.sin(2 * lng * PI)) * 2 / 3
    ret += (20 * np.sin(lat * PI) + 40 *
            np.sin(lat / 3 * PI)) * 2 / 3
    ret += (160 * np.sin(lat / 12 * PI) + 320 *
            np.sin(lat * PI / 30.0)) * 2 / 3
    return ret


def _transformlng(coordinates):
    lng = coordinates[:, 0] - 105
    lat = coordinates[:, 1] - 35
    ret = 300 + lng + 2 * lat + 0.1 * lng * lng + \
          0.1 * lng * lat + 0.1 * np.sqrt(np.fabs(lng))
    ret += (20 * np.sin(6 * lng * PI) + 20 *
            np.sin(2 * lng * PI)) * 2 / 3
    ret += (20 * np.sin(lng * PI) + 40 *
            np.sin(lng / 3 * PI)) * 2 / 3
    ret += (150 * np.sin(lng / 12 * PI) + 300 *
            np.sin(lng / 30 * PI)) * 2 / 3
    return ret


def gcj02_to_wgs84(coordinates):
    """
    GCJ-02转WGS-84
    :param coordinates: GCJ-02坐标系的经度和纬度的numpy数组
    :returns: WGS-84坐标系的经度和纬度的numpy数组
    """
    ee = 0.006693421622965943  # 偏心率平方
    a = 6378245  # 长半轴
    lng = coordinates[:, 0]
    lat = coordinates[:, 1]
    is_in_china = (lng > 73.66) & (lng < 135.05) & (lat > 3.86) & (lat < 53.55)
    _transform = coordinates[is_in_china]  # 只对国内的坐标做偏移

    dlat = _transformlat(_transform)
    dlng = _transformlng(_transform)
    radlat = _transform[:, 1] / 180 * PI
    magic = np.sin(radlat)
    magic = 1 - ee * magic * magic
    sqrtmagic = np.sqrt(magic)
    dlat = (dlat * 180.0) / ((a * (1 - ee)) / (magic * sqrtmagic) * PI)
    dlng = (dlng * 180.0) / (a / sqrtmagic * np.cos(radlat) * PI)
    mglat = _transform[:, 1] + dlat
    mglng = _transform[:, 0] + dlng
    coordinates[is_in_china] = np.array([
        _transform[:, 0] * 2 - mglng, _transform[:, 1] * 2 - mglat
    ]).T
    return coordinates


def bd09_to_gcj02(coordinates):
    """
    BD-09转GCJ-02
    :param coordinates: BD-09坐标系的经度和纬度的numpy数组
    :returns: GCJ-02坐标系的经度和纬度的numpy数组
    """
    x_pi = PI * 3000 / 180
    x = coordinates[:, 0] - 0.0065
    y = coordinates[:, 1] - 0.006
    z = np.sqrt(x * x + y * y) - 0.00002 * np.sin(y * x_pi)
    theta = np.arctan2(y, x) - 0.000003 * np.cos(x * x_pi)
    lng = z * np.cos(theta)
    lat = z * np.sin(theta)
    coordinates = np.array([lng, lat]).T
    return coordinates


def bd09_to_wgs84(coordinates):
    """
    BD-09转WGS-84
    :param coordinates: BD-09坐标系的经度和纬度的numpy数组
    :returns: WGS-84坐标系的经度和纬度的numpy数组
    """
    return gcj02_to_wgs84(bd09_to_gcj02(coordinates))


def mercator_to_bd09(mercator):
    """
    BD-09MC转BD-09
    :param coordinates: GCJ-02坐标系的经度和纬度的numpy数组
    :returns: WGS-84坐标系的经度和纬度的numpy数组
    """
    MCBAND = [12890594.86, 8362377.87, 5591021, 3481989.83, 1678043.12, 0]
    MC2LL = [[1.410526172116255e-08, 8.98305509648872e-06, -1.9939833816331,
              200.9824383106796, -187.2403703815547, 91.6087516669843,
              -23.38765649603339, 2.57121317296198, -0.03801003308653,
              17337981.2],
             [-7.435856389565537e-09, 8.983055097726239e-06, -0.78625201886289,
              96.32687599759846, -1.85204757529826, -59.36935905485877,
              47.40033549296737, -16.50741931063887, 2.28786674699375,
              10260144.86],
             [-3.030883460898826e-08, 8.98305509983578e-06, 0.30071316287616,
              59.74293618442277, 7.357984074871, -25.38371002664745,
              13.45380521110908, -3.29883767235584, 0.32710905363475,
              6856817.37],
             [-1.981981304930552e-08, 8.983055099779535e-06, 0.03278182852591,
              40.31678527705744, 0.65659298677277, -4.44255534477492,
              0.85341911805263, 0.12923347998204, -0.04625736007561,
              4482777.06],
             [3.09191371068437e-09, 8.983055096812155e-06, 6.995724062e-05,
              23.10934304144901, -0.00023663490511, -0.6321817810242,
              -0.00663494467273, 0.03430082397953, -0.00466043876332,
              2555164.4],
             [2.890871144776878e-09, 8.983055095805407e-06, -3.068298e-08,
              7.47137025468032, -3.53937994e-06, -0.02145144861037,
              -1.234426596e-05, 0.00010322952773, -3.23890364e-06,
              826088.5]]

    x = np.abs(mercator[:, 0])
    y = np.abs(mercator[:, 1])
    coef = np.array([
        MC2LL[index] for index in
        (np.tile(y.reshape((-1, 1)), (1, 6)) < MCBAND).sum(axis=1)
    ])
    return converter(x, y, coef)


def converter(x, y, coef):
    x_temp = coef[:, 0] + coef[:, 1] * np.abs(x)
    x_n = np.abs(y) / coef[:, 9]
    y_temp = coef[:, 2] + coef[:, 3] * x_n + coef[:, 4] * x_n ** 2 + \
             coef[:, 5] * x_n ** 3 + coef[:, 6] * x_n ** 4 + coef[:, 7] * x_n ** 5 + \
             coef[:, 8] * x_n ** 6
    x[x < 0] = -1
    x[x >= 0] = 1
    y[y < 0] = -1
    y[y >= 0] = 1
    x_temp *= x
    y_temp *= y
    coordinates = np.array([x_temp, y_temp]).T
    return coordinates


def LL2NE(lat0, lon0, lat, lon):
    Re=6378140.0
    n=len(lat)
    x_N=n*[0]
    y_E=n*[0]
    for i in range(n):
        delta_lon=lon[i]-lon0
        delat_lat=lat[i]-lat0
        x_N[i]=Re*delat_lat
        y_E[i]=Re*math.cos(lat0)*delta_lon

    return x_N, y_E

########################################################################将地铁站点信息存成txt
data = []  # 绘制数据
marked = set()
# cnt = 0
# print(station_info_json)

#利用正则表达式查找地铁线路的号数
pattern=re.compile(r'\d+')

deg2rad=math.pi/180
lat_c=30.6*deg2rad
lon_c=104.1*deg2rad
plt.figure(figsize=(10,8),dpi=150)
for line in station_info_json['content']:
    line_name=line['line_name']
    line_num_str_list=pattern.findall(line_name)
    if (len(line_num_str_list)==0):#如果为空，则舍弃当前线路（“最近”新修的）
        continue
    else:
        line_num=eval(line_num_str_list[0])
    uid = line['line_uid']
    if uid in marked:  # 由于线路包括了来回两个方向，需要排除已绘制线路的反向线路
        continue

    plots = []  # 站台BD-09MC坐标
    plots_name = []  # 站台名称

    for plot in line['stops']:
        plots.append([plot['x'], plot['y']])
        plots_name.append(plot['name'])

    # 站点名
    df1 = pd.DataFrame(columns=[''], data=plots_name)

    plot_mercator = np.array(plots)

    plot_coordinates = bd09_to_wgs84(mercator_to_bd09(plot_mercator))  # 站台经纬度

    list_lonlat = plot_coordinates.tolist()

    # 站点经纬度
    df2 = pd.DataFrame(columns=['', ''], data=list_lonlat)
    lon=[]
    lat=[]
    for i in range(len(list_lonlat)):
        lon.append(deg2rad*list_lonlat[i][0])
        lat.append(deg2rad*list_lonlat[i][1])

    [x_N,y_E]=LL2NE(lat_c,lon_c,lat,lon)
    plt.plot(y_E, x_N,':',linewidth=1)
    plt.plot(y_E, x_N, marker='.', linewidth=0.3)

    df4 = pd.DataFrame(columns=[''],data=[line_num]*len(plots_name))
    df3 = pd.concat([df1, df2, df4], axis=1)

    #将地铁站点到txt中，用于后续的规划算法
    df3.to_csv('ChengduMetroStops.txt', mode='a', sep=' ', index=False, encoding='utf-8')
    # df3.to_csv('cdmerto_sites.csv', mode='a', index=False, encoding='GB18030')
    # csv_to_excel = pd.read_csv('cdmerto_sites.csv', encoding='GB18030')
    # csv_to_excel.to_excel('cdmerto_sites.xlsx', sheet_name='Sheet1', index=False)

    # df3.to_csv('ChengduMetroStops-New.txt', sep=' ', index=0, header=0)
    marked.add(uid)  # 添加已绘制线路的uid
    marked.add(line['pair_line_uid'])  # 添加已绘制线路反向线路的uid

###################################################################调用路径规划算法规划乘车路线
s_LL_in=ctypes.c_double*2
s_LL_in=s_LL_in()
t_LL_in=ctypes.c_double*2
t_LL_in=t_LL_in()
lat_seq_out=ctypes.c_double*100
lat_seq_out=lat_seq_out()
lon_seq_out=ctypes.c_double*100
lon_seq_out=lon_seq_out()

line_seq_out=ctypes.c_int*100
line_seq_out=line_seq_out()

# 琉璃场：104.09744,30.609352
# 七中林荫：104.072403,30.637637
# 回龙：104.010087,30.446785
# 双流机场：103.953002,30.571695
# 西南交大犀浦校区：103.984528, 30.766657
# 龙泉驿：104.266385,30.562649
# 春熙路：104.077046,30.655304

s_LL_in[0]=104.077046
s_LL_in[1]=30.655304
# t_LL_in[0]=103.983056
# t_LL_in[1]=30.624659
t_LL_in[0]=103.953002
t_LL_in[1]=30.571695
# t_LL_in[0]=104.09744
# t_LL_in[1]=30.609352
# t_LL_in[0]=103.953002
# t_LL_in[1]=30.571695
print("起点：经度{}°,纬度{}°\n终点：经度{}°,纬度{}°\n".format(s_LL_in[0],s_LL_in[1],t_LL_in[0],t_LL_in[1]))

###调用路径规划函数
numpoints=lib.Plan(s_LL_in, t_LL_in, lat_seq_out, lon_seq_out, line_seq_out)

numLines=0
while (True):
    # print(line_seq_out[numLines+1])
    if (line_seq_out[numLines+1]!=-1):
        numLines+=1
    else:
        break

#线条颜色选择
color='rgbycmkw'
for i in range(numLines):
    lon = []
    lat = []
    id0=line_seq_out[i]
    id1=line_seq_out[i+1]
    lon.append(deg2rad * lon_seq_out[id0])
    lat.append(deg2rad * lat_seq_out[id0])
    for j in range(id1-id0):
        lon.append(deg2rad * lon_seq_out[id0+j+1])
        lat.append(deg2rad * lat_seq_out[id0+j+1])
    [x_N, y_E] = LL2NE(lat_c, lon_c, lat, lon)
    # plt.plot(y_E, x_N, 'o'+color[i])
    plt.plot(y_E, x_N, color[i], linewidth=3)


print("\n一共{}站".format(numpoints))
plt.xlabel("East/m",fontsize=16)
plt.ylabel("North/m",fontsize=16)
plt.grid()
plt.axis('equal')
plt.show()

3.2结果展示

3.2.1以从西南交大犀浦校区到龙泉驿为例

可以看到整体的结果是对的，但由于自己的算法内部只考虑了地铁站点之间的直线距离，没有将换乘时间考虑进去，导致换乘次数多的路线直线距离之和更短而被采纳。解决思路是在构建有向图的时候将换乘车站在各线路上作为单独节点，这些节点中间加上一个cost（取值根据换乘所用时间，以及站点之间路径cost量级设置），这样就可以避免过多的换乘

下面是自己程序规划结果，有文字输出和图片输出

高德地图输出结果

两者的区别出现在下面路段，其中红色路径为自己算法规划的结果，如果是直连的话确实是更短的，但从图上来看8号线中间存在弯折。

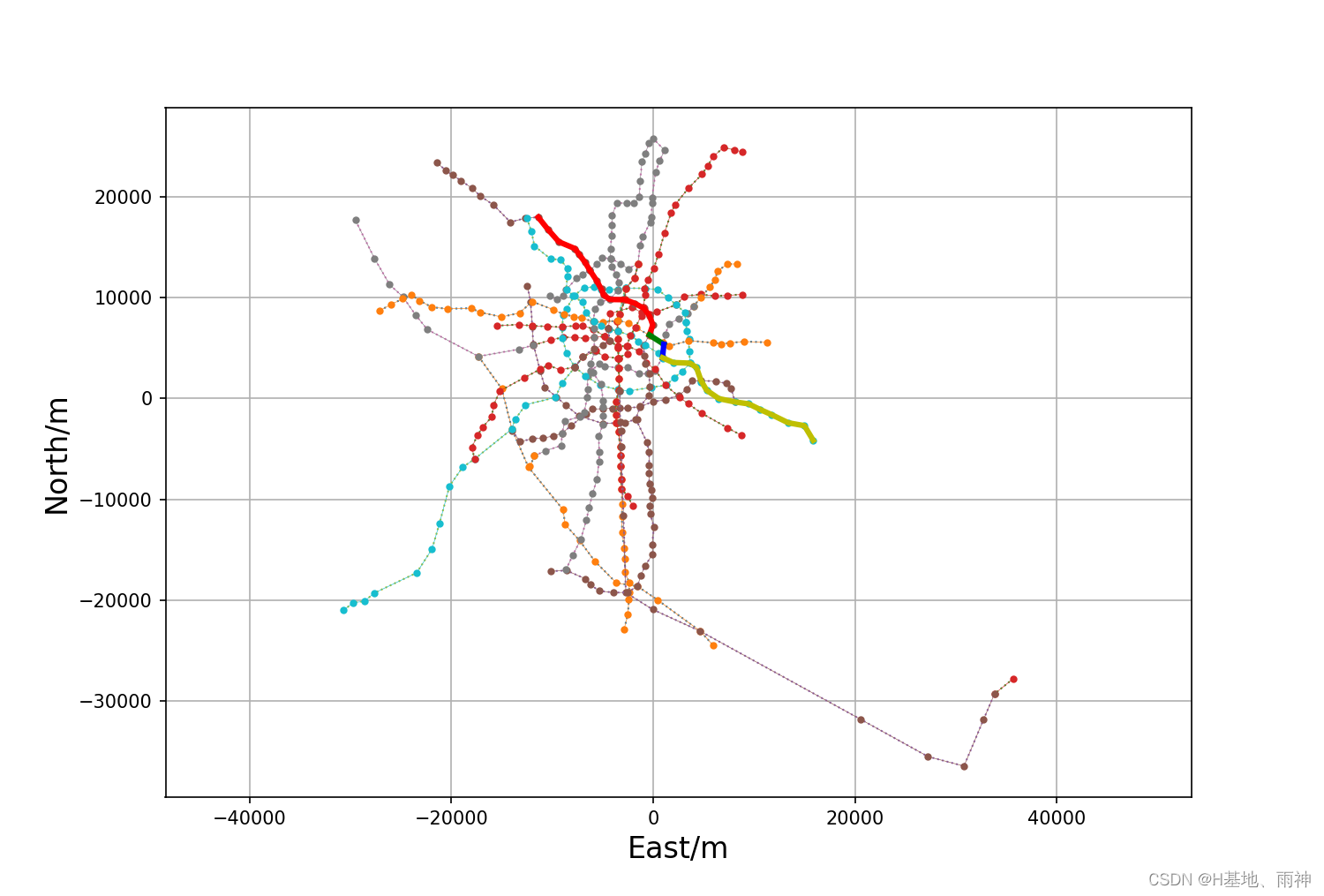
3.2.2以从春熙路到双流T2航站楼为例

路线是可达的，但是换乘次数多

高德地图规划结果：