归一化的互信息

1. （1）信息熵：对信息进行量化度量，在信源中，考虑的不是某一单个符号发生的不确定性，而是要考虑这个信源所有可能发生情况的平均不确定性。若信源符号有n种取值：U1…Ui…Un，对应概率为：P1…Pi…Pn，且各种符号的出现彼此独立。这时，信源的平均不确定性应当为单个符号不确定性-logPi的统计平均值（E），可称为信息熵，即 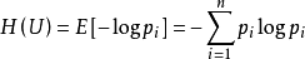，式中对数一般取2为底，单位为比特信息熵是信息论中用于度量信息量的一个概念。H(U)就被称为随机变量 xx 的熵,它是表示随机变量不确定的度量，是对所有可能发生的事件产生的信息量的期望。从公式可得，随机变量的取值个数越多，状态数也就越多，信息熵就越大，混乱程度就越大。当随机分布为均匀分布时，熵最大，且 0≤H(U)≤logn。
2. （2）相对熵：也称为KL散度，是两个概率分布之间差异的非对称性度量。在信息理论中，相对熵的值等价于两个概率的信息熵的差值。设P(x),Q(x)是随机变量 X上的两个概率分布，则在离散和连续随机变量的情形下，相对熵的定义分别为
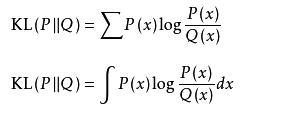   相对熵可以衡量两个随机分布之间的距离，当两个随机分布相同时，他们的相对熵就为0，当两个随机分布的差别增大时，它们的相对熵也会增大。所以相对熵可以用于比较文本的相似度，先统计出词的频率，然后计算相对熵。另外，在多指标系统评估中，指标权重分配是一个重点和难点，也通过相对熵可以处理。
3. （3）互信息：信息论里一种有用的信息度量，它可以看成是一个随机变量里包含的关于另一个随机变量的信息量，或者说是一个随机变量由于已知另一个随机变量而减少的不肯定性。设两个随机变量 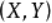的联合分布为 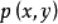，边缘分布分别为 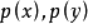，互信息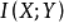 是联合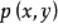分布 与边缘分布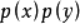 的相对熵， 即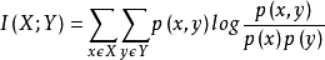
4. （5）归一化的互信息：Normalized Mutual Information(NMI)通常用在聚类中，度量2个聚类结果的相近程度。