序列模型
引用翻译:《动手学深度学习》
人们对电影的意见可以随着时间的推移而发生相当大的变化。事实上,心理学家甚至为其中的一些影响命名。
有一种锚定,基于别人的意见。例如,在奥斯卡颁奖之后,相应电影的评分会上升,尽管它仍然是同一部电影。这种效应持续了几个月,直到奖项被遗忘。
还有Hedonic适应,人类很快就会适应,接受一个改善的(或一个坏的)情况作为新的常态。例如,在看了许多好电影后,对下一部电影同样好或更好的期望很高,即使是一部普通的电影,在许多伟大的电影之后也可能被认为是一部坏电影。
还有就是季节性。很少有观众喜欢在八月看一部圣诞老人的电影。在某些情况下,由于导演或演员在制作过程中的不当行为,电影变得不受欢迎。
有些电影成为邪典电影,因为它们几乎是滑稽的糟糕。来自外太空的9号计划》和《巨魔2》因为这个原因取得了很高的声望。
简而言之,收视率并不是静止的。使用时间动态有助于Koren.2009更准确地推荐电影。但这不仅仅是关于电影。
许多用户在打开应用程序的时间方面有非常特殊的行为。例如,社交媒体应用程序在放学后更受学生欢迎。股市交易应用程序在市场开放时更常被使用。
预测明天的股票价格比为我们昨天错过的股票价格填空要难得多,尽管两者都只是估计一个数字的问题。毕竟,事后诸葛亮比事前诸葛亮要容易得多。在统计学中,前者被称为预测,而后者则被称为过滤。
音乐、语音、文字、电影、步骤等在本质上都是有顺序的。如果我们对它们进行排列组合,它们就没有什么意义了。头条新闻狗咬人比人咬狗更不令人惊讶,尽管文字是相同的。
地震有很强的关联性,也就是说,在一次大地震之后,很可能会有几次较小的余震,比没有强震时要多得多。事实上,地震是时空相关的,也就是说,余震通常在很短的时间内发生,而且距离很近。
人类之间的互动是有顺序的,从推特上的争吵、舞蹈模式和辩论中就可以看出这一点。
一、统计学工具
简而言之,我们需要统计工具和新的深度网络架构来处理序列数据。为了简单起见,我们以股票价格为例。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-8DRyQ3dB-1653393853137)(…/img/ftse100.png)]
让我们用 x t ≥ 0 x_t \geq 0 xt≥0来表示价格,即在时间𝑡∈ℕ我们观察到一些价格 x t x_t xt。对于一个交易者来说,要想在第四天的股票市场上取得好成绩,他应该想通过以下方式来预测𝑥𝑡
x t ∼ p ( x t ∣ x t − 1 , … x 1 ) . x_t \sim p(x_t|x_{t-1}, \ldots x_1). xt∼p(xt∣xt−1,…x1).。
二、自回归模型
为了实现这一目标,我们的交易员可以使用一个回归器。只是有一个很大的问题–输入的数量, x t − 1 , … x 1 x_{t-1}, \ldots x_1 xt−1,…x1是变化的,取决于𝑡。也就是说,这个数字会随着我们遇到的数据量的增加而增加,我们将需要一个近似值来使其在计算上可操作。本章的大部分内容将围绕如何有效地估计 p ( x t ∣ x t − 1 , … x 1 ) p(x_t|x_{t-1}, \ldots x_1) p(xt∣xt−1,…x1)。简而言之,这可以归结为两种策略。
假设可能相当长的序列
x
t
−
1
,
…
x
1
x_{t-1}, \ldots x_1
xt−1,…x1并不是真的需要。在这种情况下,我们可以满足于某个时间跨度𝜏,只使用
x
t
−
1
,
…
x
t
−
τ
x_{t-1}, \ldots x_{t-\tau}
xt−1,…xt−τ的观测值。直接的好处是,现在参数的数量总是相同的,至少对于𝑡>𝜏。这使得我们可以训练一个如上所述的深度网络。这样的模型将被称为自回归模型,因为它们实际上是对自己进行回归。
另一种策略是尝试保留一些过去观察结果的摘要ℎ𝑡,并在实际预测的基础上更新。这就导致了估计
x
t
∣
x
t
−
1
,
h
t
−
1
x_t|x_{t-1}, h_{t-1}
xt∣xt−1,ht−1的模型,而且是ℎ𝑡=𝑔(ℎ𝑡,𝑥𝑡)的更新。由于ℎ𝑡从未被观测到,这些模型也被称为潜在自回归模型。LSTM和GRU就是这样的例子。
这两种情况都提出了一个明显的问题,即如何产生训练数据。我们通常使用历史观测数据来预测到现在为止的下一个观测数据。显然,我们并不期望时间是静止的。然而,一个常见的假设是,虽然𝑥的具体数值可能会改变,但至少时间序列本身的动态不会改变。这是合理的,因为新的动态就是这样,是新的,因此用我们目前掌握的数据是无法预测的。统计学家把不改变的动态称为静止的。不管我们怎么做,我们将通过以下方式得到整个时间序列的估计值
p ( x 1 , … x T ) = ∏ t = 1 T p ( x t ∣ x t − 1 , … x 1 ) . p(x_1, \ldots x_T) = \prod_{t=1}^T p(x_t|x_{t-1}, \ldots x_1). p(x1,…xT)=t=1∏Tp(xt∣xt−1,…x1).
请注意,如果我们处理的是离散的对象,比如说单词,而不是数字,那么上述考虑仍然成立。唯一不同的是,在这种情况下,我们需要使用分类器而不是回归器来估计 p ( x t ∣ x t − 1 , … x 1 ) p(x_t| x_{t-1}, \ldots x_1) p(xt∣xt−1,…x1).。
三、马尔科夫模型
回顾一下近似,在自回归模型中,我们只用(𝑥𝑡-1,…𝑥𝑡-𝜏)而不是(𝑥𝑡-1,…𝑥1)来估计𝑥𝑡。只要这种近似是准确的,我们就说该序列满足马尔科夫条件。特别是,如果𝜏=1,我们就有一个一阶Markov模型,𝑝(𝑥)由以下公式给出
p ( x 1 , … x T ) = ∏ t = 1 T p ( x t ∣ x t − 1 ) . p(x_1, \ldots x_T) = \prod_{t=1}^T p(x_t|x_{t-1}). p(x1,…xT)=t=1∏Tp(xt∣xt−1).
当𝑥𝑡只承担离散值时,这样的模型特别好,因为在这种情况下,可以用动态编程来精确地计算沿链的值。例如,我们可以有效地计算 x t + 1 ∣ x t − 1 x_{t+1}|x_{t-1} xt+1∣xt−1,因为我们只需要考虑过去观察的很短的历史。
p ( x t + 1 ∣ x t − 1 ) = ∑ x t p ( x t + 1 ∣ x t ) p ( x t ∣ x t − 1 ) p(x_{t+1}|x_{t-1}) = \sum_{x_t} p(x_{t+1}|x_t) p(x_t|x_{t-1}) p(xt+1∣xt−1)=xt∑p(xt+1∣xt)p(xt∣xt−1)
探讨动态编程的细节已经超出了本节的范围。控制和强化学习算法广泛地使用这种工具。
四、因果关系
原则上,以相反的顺序展开𝑝(𝑥1,…𝑥𝑇)并没有错。毕竟,通过调节,我们总是可以通过以下方式来写它
p ( x 1 , … x T ) = ∏ t = T 1 p ( x t ∣ x t + 1 , … x T ) . p(x_1, \ldots x_T) = \prod_{t=T}^1 p(x_t|x_{t+1}, \ldots x_T). p(x1,…xT)=t=T∏1p(xt∣xt+1,…xT).
事实上,如果我们有一个马尔科夫模型,我们也可以得到一个反向的条件概率分布。然而,在许多情况下,数据存在一个自然的方向,即在时间上往前走。
很明显,未来的事件不可能影响过去。因此,如果我们改变𝑥𝑡,我们可能会影响到𝑥𝑡+1向前发生的事情,但反之则不会。也就是说,如果我们改变𝑥𝑡,过去事件的分布就不会改变。
因此,解释𝑥𝑡+1|𝑥𝑡应该比解释𝑥𝑡|𝑥𝑡+1更容易。
例如,Hoyer等人在2008年的研究表明,在某些情况下,我们可以找到𝑥𝑡+1=𝑓(𝑥𝑡)+𝜖的一些加性噪声,而相反的情况则不成立。
这是个好消息,因为我们感兴趣的通常是估计前进方向。关于这个话题的更多信息,请参见Peters、Janzing和Schölkopf的书,2015。我们几乎没有触及它的表面。
五、实践
说了这么多理论,让我们在实践中试试吧。让我们从生成一些数据开始。为了保持简单,我们通过使用正弦函数和一些加性噪声来生成我们的 “时间序列”。
%matplotlib inline
from IPython import display
import matplotlib.pyplot as plt
import torch
import torch.nn as nn
import torch.utils.data
display.set_matplotlib_formats('svg') # 以'svg'格式显示matplotlib的内联图。
embedding = 4 # 自回归模型的嵌入维度
T = 1000 # 生成1000个点
time = torch.arange(0.0,T)
x = torch.sin(0.01 * time) + 0.2*torch.randn(T)
plt.plot(time.numpy(), x.numpy())
接下来我们需要把这个 "时间序列 "变成网络可以训练的数据。基于嵌入维度𝜏,我们将数据映射成一对𝑦𝑡=𝑥𝑡和𝐳𝑡=(𝑥𝑡-1,…𝑥𝑡-𝜏)。精明的读者可能已经注意到,这让我们的数据点减少了𝜏,因为我们没有足够的历史记录来处理其中的第一个𝜏。
一个简单的解决方法,特别是在时间序列很长的情况下,就是丢弃这几个条款。或者,我们可以用零来填充时间序列。下面的代码与前几节的训练代码基本相同。
构建数据集:
features = torch.zeros((T-embedding, embedding))
for i in range(embedding):
features[:,i] = x[i:T-embedding+i]
labels = x[embedding:]
ntrain = 600
train_data = torch.utils.data.TensorDataset(features[:ntrain,:], labels[:ntrain])
test_data = torch.utils.data.TensorDataset(features[ntrain:,:], labels[ntrain:])
# 数据集样式:features相当于输入的四个特征,是该时刻的前四个时刻的值作为特征输入
features
输出:
tensor([[ 0.0182, -0.1844, 0.0910, 0.2726],
[-0.1844, 0.0910, 0.2726, -0.0459],
[ 0.0910, 0.2726, -0.0459, 0.1509],
...,
[-0.2313, -0.2208, -0.3787, -0.6308],
[-0.2208, -0.3787, -0.6308, -0.3218],
[-0.3787, -0.6308, -0.3218, -0.7375]])
标签:
# labels是当前时刻的值作为标签,由于前embedding是没有足够历史数据的,所以会被缺失
labels[0:10]
输出:
tensor([-0.0459, 0.1509, -0.1600, 0.0933, 0.4947, 0.1816, 0.2682, 0.0742,
0.3193, 0.6376])
# 此后就类似线性回归的处理方式,建立回归模型
# 用于初始化网的权重的函数
def init_weights(m):
if type(m) == nn.Linear:
torch.nn.init.xavier_uniform_(m.weight)
# MLP架构
def get_net():
net = nn.Sequential()
net.add_module('Linear_1', nn.Linear(4, 10, bias = False))
net.add_module('relu1', nn.ReLU())
net.add_module('Linear_2', nn.Linear(10, 10, bias = False))
net.add_module('relu2', nn.ReLU())
net.add_module('final', nn.Linear(10, 1, bias = False))
net.apply(init_weights)
return net
loss = nn.MSELoss() # L2损失在Pytorch中被称为MSELoss
保持了相当简单的架构。全连接网络的几层,ReLU激活和ℓ2损失。
# 使用Adam的简单优化器,随机洗牌,迷你批大小为16。
def train_net(net, data, loss, epochs, learningrate):
batch_size = 16
trainer = torch.optim.Adam(net.parameters(), lr= learningrate)
data_iter = torch.utils.data.DataLoader(data, batch_size = batch_size, shuffle=True)
for epoch in range(1, epochs + 1):
running_loss = 0.0
for X, y in data_iter:
trainer.zero_grad()
output = net(X)
los = loss(output,y.reshape(-1,1))
los.backward()
trainer.step()
running_loss += los.item()
print('epoch %d, loss: %f' % (epoch, running_loss))
return net
net = get_net()
net = train_net(net, train_data, loss, 10, 0.01)
l = loss(net(test_data[:][0]), test_data[:][1].reshape(-1,1))
print('test loss: %f' % l.mean().detach().numpy())
epoch 1, loss: 9.772292
epoch 2, loss: 2.436983
epoch 3, loss: 2.322160
epoch 4, loss: 2.230930
epoch 5, loss: 2.200292
epoch 6, loss: 2.162730
epoch 7, loss: 2.188365
epoch 8, loss: 2.217834
epoch 9, loss: 2.137205
epoch 10, loss: 2.178516
test loss: 0.060590
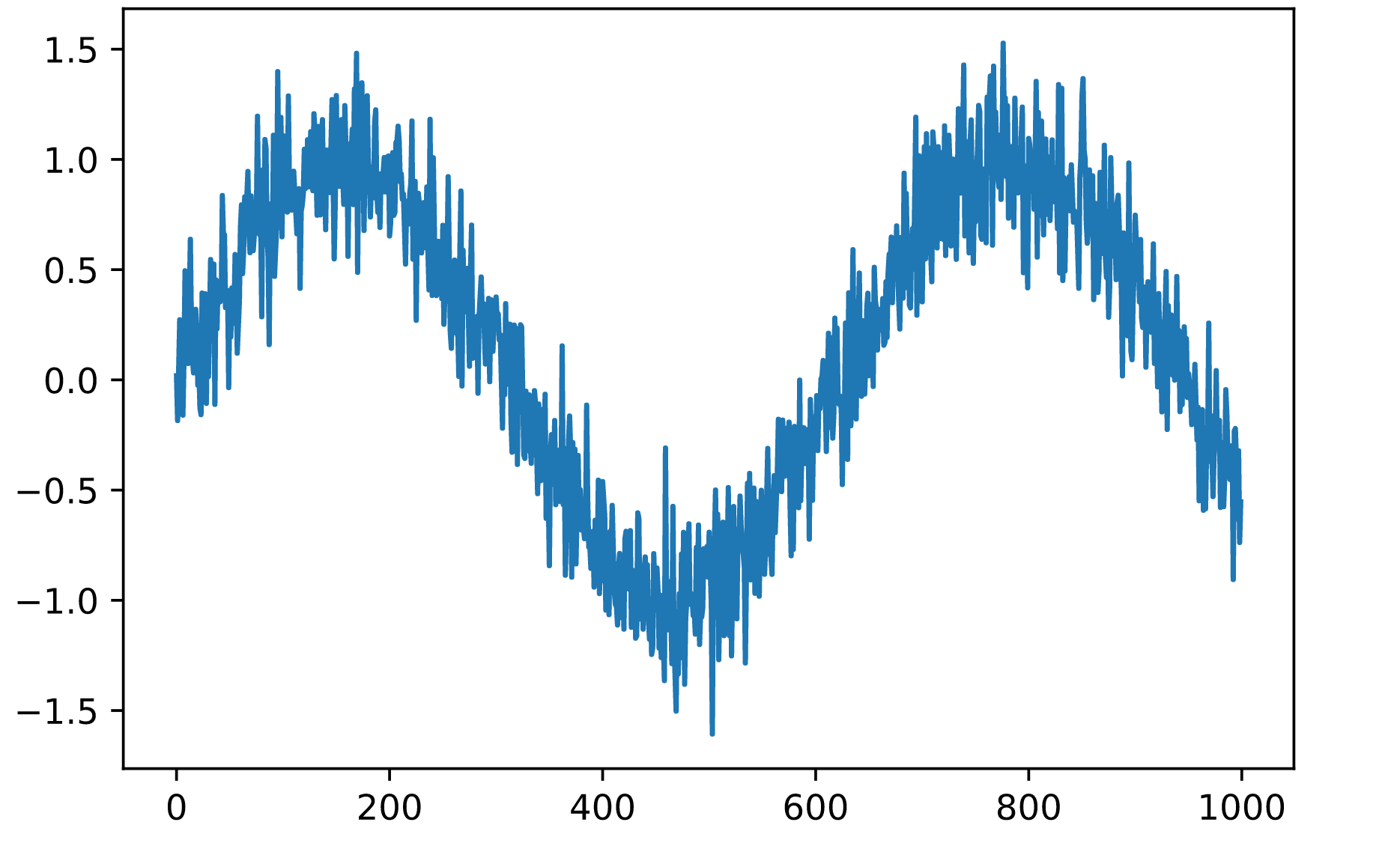
训练和测试的损失都很小,我们期望我们的模型能够很好地工作。让我们看看这在实践中意味着什么。首先要检查的是模型对下一个时间段所发生的事情的预测能力如何。
estimates = net(features)
plt.plot(time.numpy(), x.numpy(), label='data');
plt.plot(time[embedding:].numpy(), estimates.detach().numpy(), label='estimate');
plt.legend();
六、预测
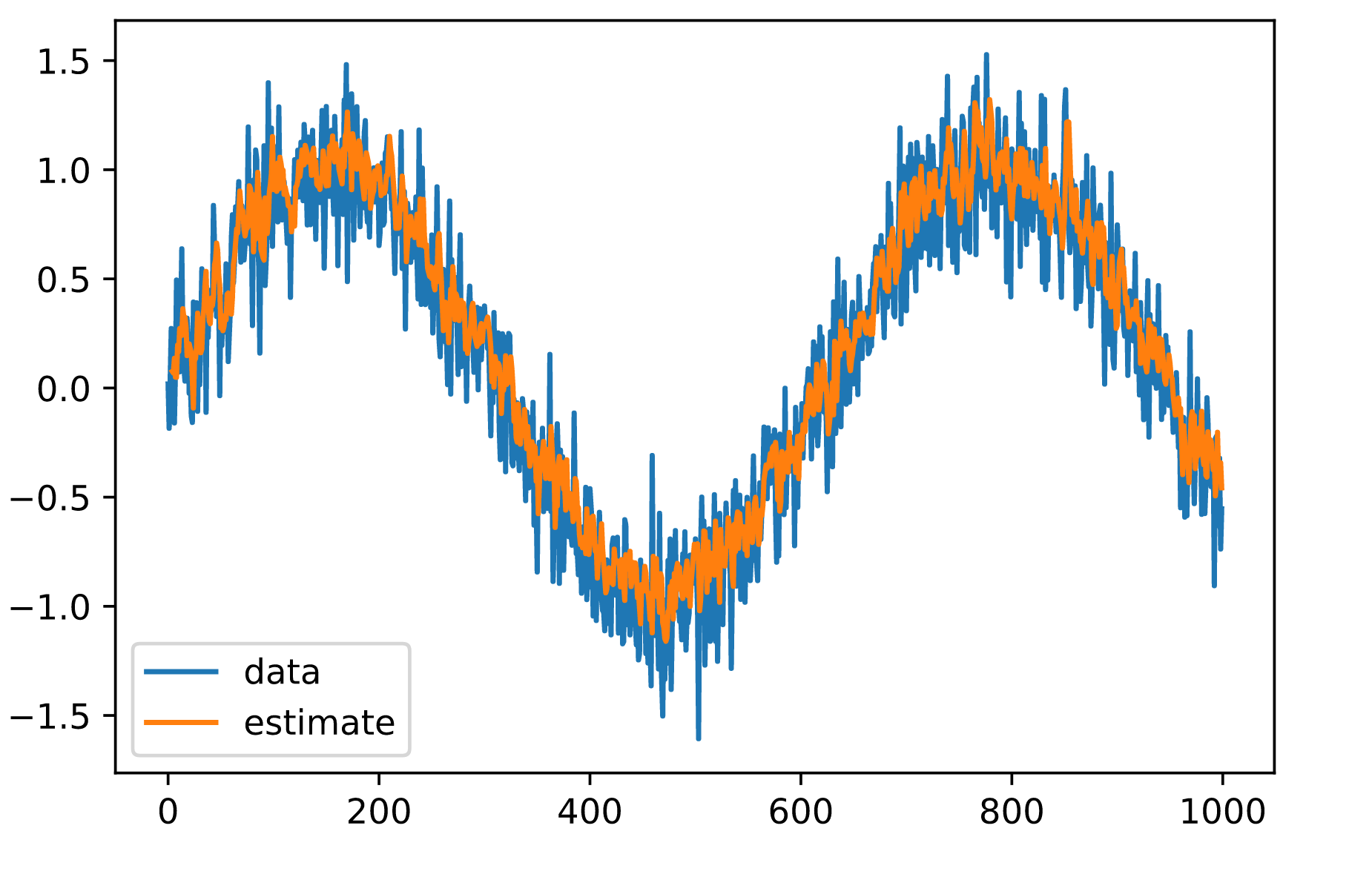
这看起来不错,就像我们所期望的那样。即使超过600个观测值,估计值看起来仍然相当可信。这其中只有一个小问题–如果我们只观察到时间步骤600之前的数据,我们就不能希望得到所有未来预测的基础真理。相反,我们需要一步一步地前进。
x 601 = f ( x 600 , … , x 597 ) x 602 = f ( x 601 , … , x 598 ) x 603 = f ( x 602 , … , x 599 ) \begin{aligned} x_{601} & = f(x_{600}, \ldots, x_{597}) \\ x_{602} & = f(x_{601}, \ldots, x_{598}) \\ x_{603} & = f(x_{602}, \ldots, x_{599}) \end{aligned} x601x602x603=f(x600,…,x597)=f(x601,…,x598)=f(x602,…,x599)
换句话说,很快我们就得用自己的预测来做未来的预测。让我们看看这一切有多顺利。
predictions = torch.zeros_like(estimates)
predictions[:(ntrain-embedding)] = estimates[:(ntrain-embedding)]
for i in range(ntrain-embedding, T-embedding):
predictions[i] = net(
predictions[(i-embedding):i].reshape(1,-1)).reshape(1)
plt.plot(time.numpy(), x.numpy(), label='data');
plt.plot(time[embedding:].numpy(), estimates.detach().numpy(), label='estimate');
plt.plot(time[embedding:].numpy(), predictions.detach().numpy(),
label='multistep');
plt.legend();
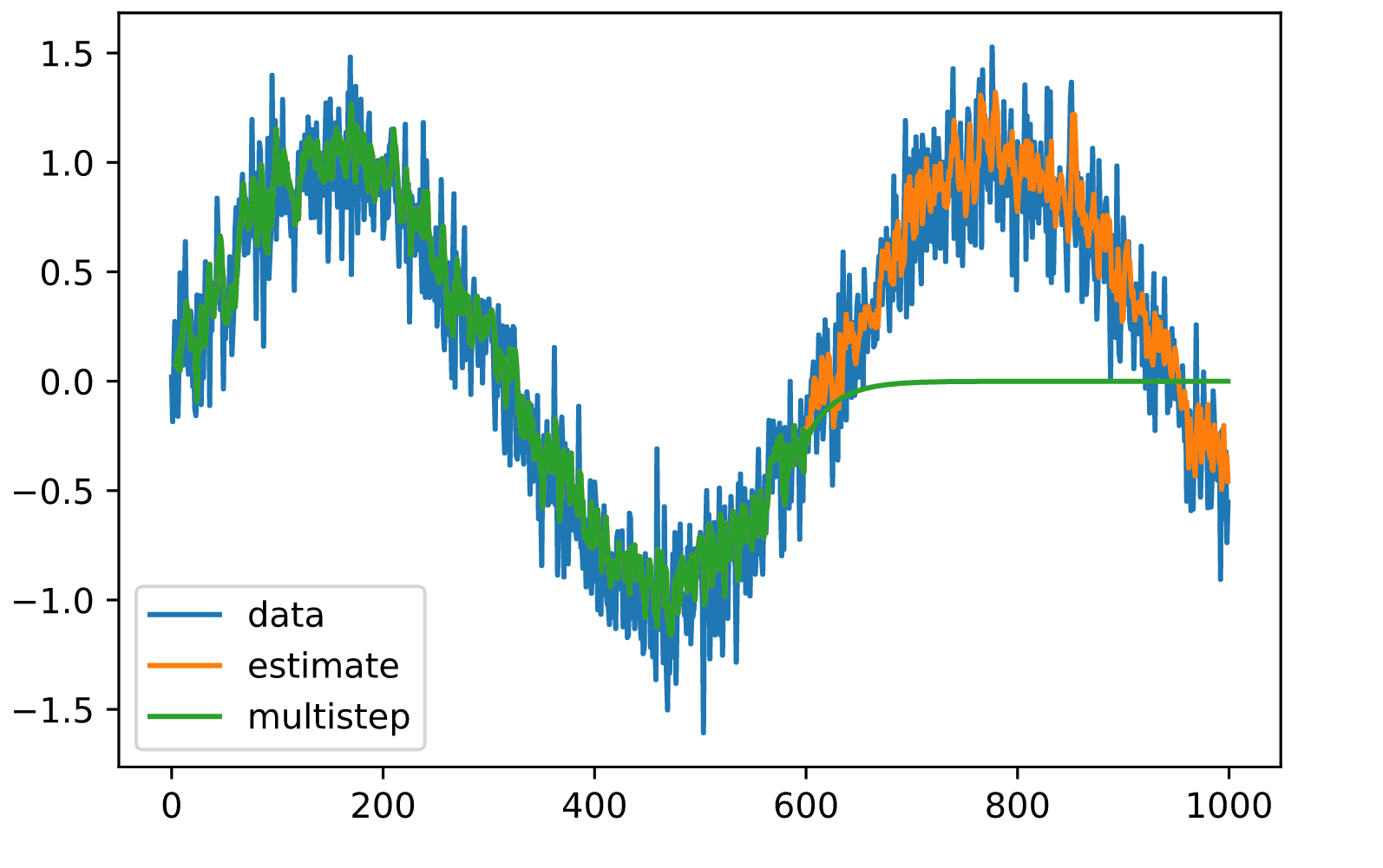
正如上面的例子所示,这是一个惊人的失败。在几个预测步骤之后,估计值很快就衰减到了0。为什么该算法的效果如此之差?
这最终是由于误差的积累。假设在第1步之后,我们有一些误差𝜖1=𝜖¯。现在第2步的输入受到了𝜖1的扰动,因此我们遭受了一些误差,其顺序为𝜖2=𝜖¯+𝐿𝜖1,依此类推。
误差可能会迅速偏离真实观测值。这是一个常见的现象–例如,未来24小时的天气预报往往是相当准确的,但超过这个时间,其准确性就会迅速下降。我们将在本章及以后的章节中讨论改善这种情况的方法。
让我们通过计算整个序列的𝑘步预测来验证这一观察。
k = 33 # Look up to k - embedding steps ahead
features = torch.zeros((T-k, k))
for i in range(embedding):
features[:,i] = x[i:T-k+i]
for i in range(embedding, k):
features[:,i] = net(features[:,(i-embedding):i]).reshape((-1))
for i in (4, 8, 16, 32):
plt.plot(time[i:T-k+i].numpy(), features[:,i].detach().numpy(),
label=('step ' + str(i)))
plt.legend();
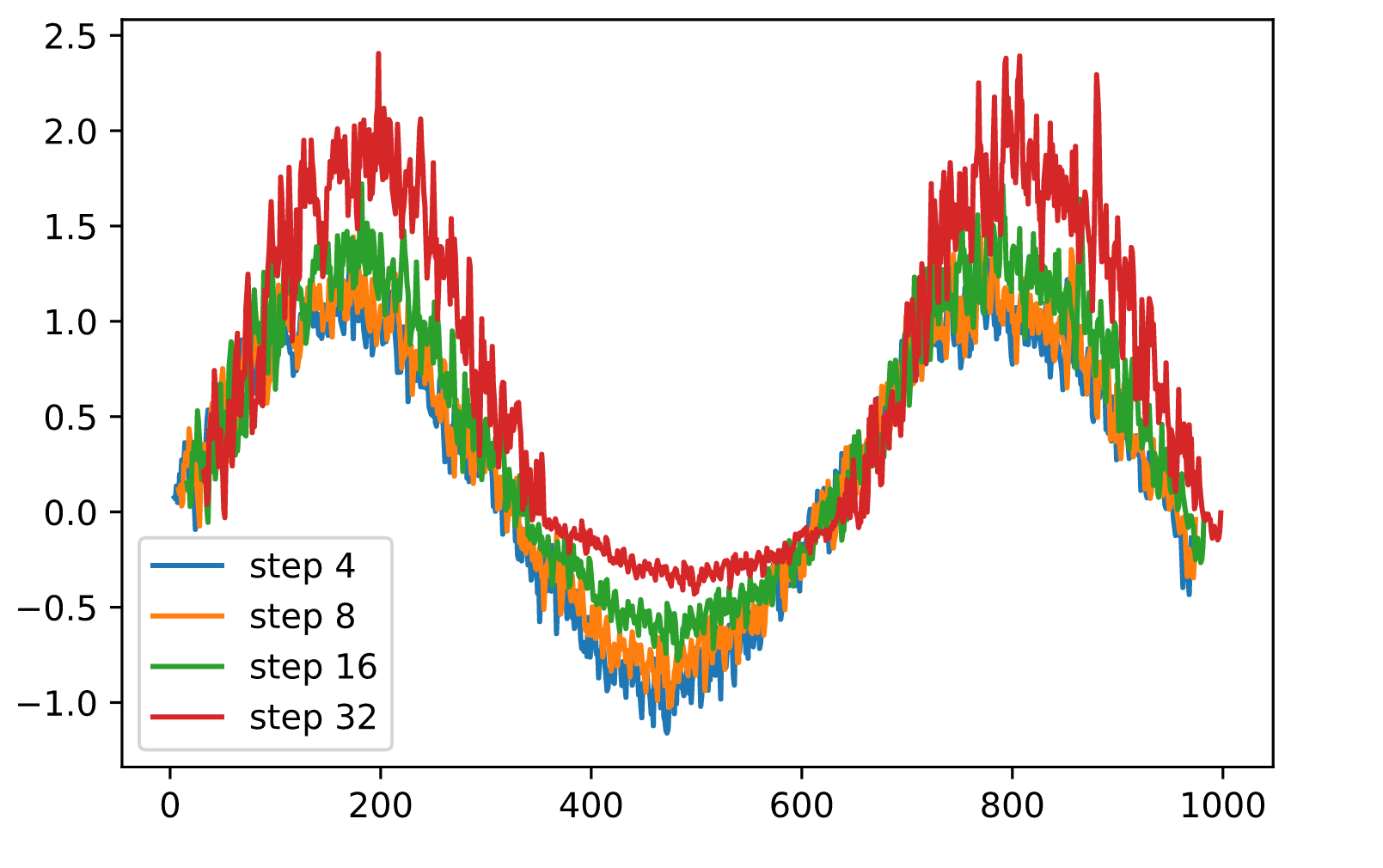
这清楚地说明了当我们试图进一步预测未来时,估计的质量如何变化。虽然8个步骤的预测仍然很好,但超过这个阶段的预测就很无用了。
七、摘要
1、序列模型需要专门的统计工具来进行估计。两个流行的选择是自回归模型和潜在变量自回归模型。
2、随着我们对时间的进一步预测,误差会累积,估计的质量会下降,往往是急剧下降。
3、填补序列中的空白(平滑)和预测之间有相当大的难度差异。因此,如果你有一个时间序列,在训练时一定要尊重数据的时间顺序,也就是说,不要在未来的数据上进行训练。
4、对于因果模型(例如,时间往前走),估计前进方向通常比反方向容易得多,也就是说,我们可以用更简单的网络来搞定。
八、常见问题
1、在常规范围内tau是不是越大越好,比如tau=5是不是比4好?
答:是,理论来说获得以往数据越多,信息越多。但是需要权衡的是:tau越大,那训练集数据变少了,比如tau直接等于时间长度,那样就只有一个训练集了。
2、RNN是采用了隐马尔可夫假设实现的。
九、练习
1、改进上述模型。
- 纳入比过去4次观察更多的内容?你真正需要多少个?
- 如果没有噪声,你需要多少个?提示–你可以把sin和cos写成一个微分方程。
- 你能在保持特征总数不变的情况下纳入较早的特征吗?这是否能提高精确度?为什么?
- 改变架构,看看会发生什么。
2、一个投资者想找到一个好的证券来购买。她看着过去的回报来决定哪一个有可能做得好。这个策略有什么可能出错?
3、因果关系是否也适用于文本?在什么程度上?
4、请举例说明什么时候需要一个潜变量自回归模型来捕捉数据的动态。






















 2542
2542











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








