关于sora的技术,看这一篇就够了
文章目录
一、sora的横空出世
openai在某一天突然宣布了一款能够文生图的大模型即将进入公测阶段,并宣称能够未来能够通过技术,构建世界模型,引起外界关注。

二、sora的训练逻辑


将其中的sora模型抽象出来,整个完整的模型框架如下所示:

首先将输入视频数据通过VAE(Variational Autoencoder,变分自动编码器)中的编码器模块编码成低维的空间向量表示,经Patches网络,将其中的向量分割为指定大小的模块(例如:16*16*16),并将时空模块通过SD模型进行扩散学习,将经过学习后的数据通过多层的以U-net为backbone的transformer网络恢复成原有大小模块,合并后得到需要的向量表示,最后逆向通过VAE解码器将向量表示输出成指定格式和时长的视频。
整个模型中主要有三大模块组成:VAE、StableDiffusion、Scaling Transformers,中间作为桥梁进行连接的是:patches和multi-condition
三、三大模块和patches
3.1 VAE
VAE是一种基于变分推断(Variational Inference, Variational Bayesian methods)的概率模型(Probabilistic Model),它属于生成模型(当然也是无监督模型)。在变分推断中,除了已知的数据(观测数据,训练数据)外还存在一个隐含变量,这里已知的数据集记为 X = { x i } i = 0 N X=\{x^{i}\}_{i=0}^N X={xi}i=0N由 N N N个连续变量或者离散变量 x x x组成,而未观测的随机变量记为 z z z,那么数据的产生包含两个过程:
- 从一个先验分布 p θ ( z ) p_{\theta}(z) pθ(z)中采样一个 z i z^i zi;
- 根据条件分布 p θ ( x ∣ z ) p_{\theta}(x|z) pθ(x∣z),用 z i z^i zi生成 x i x^i xi。
这里的
θ
\theta
θ指的是分布的参数,比如对于高斯分布就是均值和标准差。我们希望找到一个参数
θ
∗
\theta^*
θ∗来最大化生成真实数据的概率:
θ
∗
=
a
r
g
max
θ
∏
i
=
0
n
p
θ
(
x
i
)
\theta^* = arg\max_{\theta}\prod_{i=0}^{n}p_{\theta}(x^i)
θ∗=argθmaxi=0∏npθ(xi)
这里
p
θ
(
x
i
)
p_{\theta}(x^i)
pθ(xi)可以通过对
z
z
z积分得到:
p
θ
(
x
i
)
=
∫
p
θ
(
x
i
∣
z
)
p
θ
(
z
)
d
z
p_{\theta}(x^i) = \int p_{\theta}(x^i|z)p_{\theta}(z)dz
pθ(xi)=∫pθ(xi∣z)pθ(z)dz
而实际上要根据上述积分是不现实的,一方面先验分布
p
θ
(
z
)
p_{\theta}(z)
pθ(z)是未知的,而且如果分布比较复杂,对
z
z
z穷举计算也是极其耗时的。为了解决这个难题,变分推断引入后验分布
p
θ
(
x
∣
z
)
p_{\theta}(x|z)
pθ(x∣z)来联合建模,根据贝叶斯公式,后验等于:
P
θ
(
z
∣
x
)
=
p
θ
(
x
∣
z
)
p
θ
(
z
)
p
θ
(
x
)
P_{\theta}(z|x) = \frac{p_{\theta}(x|z) p_{\theta}(z)}{p_{\theta}(x)}
Pθ(z∣x)=pθ(x)pθ(x∣z)pθ(z)
这样的联合建模如上图所示,实线代表的是我们想要得到的生成模型 p θ ( x ∣ z ) p θ ( z ) p_{\theta}(x|z) p_{\theta}(z) pθ(x∣z)pθ(z),其中先验分布 p θ ( z ) p_{\theta}(z) pθ(z)往往是事先定义好的(比如标准正态分布),而 p θ ( x ∣ z ) p_{\theta}(x|z) pθ(x∣z)可以用一个网络来学习,如果把 z z z 看成隐含特征,那么这个网络就可以看成一个probabilistic decoder。虚线代表的是对后验分布 p θ ( x ∣ z ) p_{\theta}(x|z) pθ(x∣z)的变分估计,记为 q ϕ ( x ∣ z ) q_{\phi }(x|z) qϕ(x∣z),它也可以用一个网络来学习,这个网络可以看成一个probabilistic encoder。
建模已经完成,下面我们来推导一下VAE的优化目标。对于估计的后验
q
ϕ
(
x
∣
z
)
q_{\phi }(x|z)
qϕ(x∣z),我们希望它接近真实的后验分布
p
θ
(
x
∣
z
)
p_{\theta}(x|z)
pθ(x∣z),评估两个分布差异最常用的方式就是计算KL散度(Kullback-Leibler divergence)。对
q
ϕ
(
x
∣
z
)
q_{\phi }(x|z)
qϕ(x∣z)和
p
θ
(
x
∣
z
)
p_{\theta}(x|z)
pθ(x∣z)计算KL散度,如下所示:
D
K
L
(
q
ϕ
(
z
∣
x
)
∣
∣
p
θ
(
z
∣
x
)
)
=
∫
q
ϕ
(
z
∣
x
)
l
o
g
q
ϕ
(
z
∣
x
)
p
θ
(
z
∣
x
)
d
z
=
∫
q
ϕ
(
z
∣
x
)
l
o
g
q
ϕ
(
z
∣
x
)
p
θ
(
x
)
p
θ
(
z
,
x
)
d
z
=
∫
q
ϕ
(
z
∣
x
)
(
l
o
g
p
θ
(
x
)
+
l
o
g
q
ϕ
(
z
∣
x
)
p
θ
(
z
,
x
)
)
d
z
=
l
o
g
q
ϕ
(
x
)
+
∫
q
ϕ
(
z
∣
x
)
l
o
g
q
ϕ
(
z
∣
x
)
p
θ
(
z
,
x
)
d
z
=
l
o
g
p
θ
(
x
)
+
∫
q
ϕ
(
z
∣
x
)
l
o
g
q
ϕ
(
z
∣
x
)
p
θ
(
x
∣
z
)
p
θ
(
z
)
d
z
=
l
o
g
p
θ
(
x
)
+
E
z
q
ϕ
(
z
∣
x
)
[
l
o
g
q
ϕ
(
z
∣
x
)
p
θ
(
z
)
−
l
o
g
p
θ
(
x
∣
z
)
]
=
l
o
g
p
θ
(
x
)
+
D
K
L
(
q
ϕ
(
z
∣
x
)
∣
∣
p
θ
(
z
)
)
−
E
z
q
ϕ
(
z
∣
x
)
l
o
g
p
θ
(
x
∣
z
)
\begin{aligned} D_{KL}(q_{\phi}(z|x)||p_{\theta}(z|x)) &= \int q_{\phi}(z|x)log\frac{q_{\phi}(z|x)}{p_{\theta}(z|x)}dz \\ &= \int q_{\phi}(z|x)log\frac{q_{\phi}(z|x)p_{\theta}(x)}{p_{\theta}(z,x) }dz \\ &= \int q_{\phi}(z|x)(log {p_{\theta}(x)} + log\frac{q_{\phi}(z|x)}{p_{\theta}(z,x) })dz \\ &= log {q_{\phi}(x)} +\int q_{\phi}(z|x) log {\frac{q_{\phi}(z|x)}{p_{\theta}(z,x)}} dz \\ &= log {p_{\theta}(x)} +\int q_{\phi}(z|x) log {\frac{q_{\phi}(z|x)}{p_{\theta}(x|z)p_{\theta}(z)}} dz \\ &= log {p_{\theta}(x)} + E_{z~q_{\phi}(z|x)}[log \frac{q_{\phi}(z|x)}{p_{\theta}(z)} - logp_{\theta}(x|z)]\\ &= log {p_{\theta}(x)} + D_{KL}(q_{\phi}(z|x)||p_{\theta}(z)) - E_{z~q_{\phi}(z|x)}logp_{\theta}(x|z) \end{aligned}
DKL(qϕ(z∣x)∣∣pθ(z∣x))=∫qϕ(z∣x)logpθ(z∣x)qϕ(z∣x)dz=∫qϕ(z∣x)logpθ(z,x)qϕ(z∣x)pθ(x)dz=∫qϕ(z∣x)(logpθ(x)+logpθ(z,x)qϕ(z∣x))dz=logqϕ(x)+∫qϕ(z∣x)logpθ(z,x)qϕ(z∣x)dz=logpθ(x)+∫qϕ(z∣x)logpθ(x∣z)pθ(z)qϕ(z∣x)dz=logpθ(x)+Ez qϕ(z∣x)[logpθ(z)qϕ(z∣x)−logpθ(x∣z)]=logpθ(x)+DKL(qϕ(z∣x)∣∣pθ(z))−Ez qϕ(z∣x)logpθ(x∣z)
最终可以得到:
D
K
L
(
q
ϕ
(
z
∣
x
)
∣
∣
p
θ
(
z
∣
x
)
)
=
l
o
g
p
θ
(
x
)
+
D
K
L
(
q
ϕ
(
z
∣
x
)
∣
∣
p
θ
(
z
)
)
−
E
z
q
ϕ
(
z
∣
x
)
l
o
g
p
θ
(
x
∣
z
)
\begin{aligned} D_{KL}(q_{\phi}(z|x)||p_{\theta}(z|x)) &= log {p_{\theta}(x)} + D_{KL}(q_{\phi}(z|x)||p_{\theta}(z)) - E_{z~q_{\phi}(z|x)}logp_{\theta}(x|z) \end{aligned}
DKL(qϕ(z∣x)∣∣pθ(z∣x))=logpθ(x)+DKL(qϕ(z∣x)∣∣pθ(z))−Ez qϕ(z∣x)logpθ(x∣z)
这里我们适当调整一下上述等式中各个项的位置,可以得到:
l
o
g
p
θ
(
x
)
−
D
K
L
(
q
ϕ
(
z
∣
x
)
∣
∣
p
θ
(
z
∣
x
)
)
=
E
z
q
ϕ
(
z
∣
x
)
l
o
g
p
θ
(
x
∣
z
)
−
D
K
L
(
q
ϕ
(
z
∣
x
)
∣
∣
p
θ
(
z
)
)
\begin{aligned} log {p_{\theta}(x)} - D_{KL}(q_{\phi}(z|x)||p_{\theta}(z|x)) &= E_{z~q_{\phi}(z|x)}logp_{\theta}(x|z) - D_{KL}(q_{\phi}(z|x)||p_{\theta}(z)) \end{aligned}
logpθ(x)−DKL(qϕ(z∣x)∣∣pθ(z∣x))=Ez qϕ(z∣x)logpθ(x∣z)−DKL(qϕ(z∣x)∣∣pθ(z))
这里
l
o
g
p
θ
(
x
)
log{p_{\theta}(x)}
logpθ(x)是生成真实数据的对数似然,对于生成模型,我们希望最大化这个对数似然,而
D
K
L
(
q
ϕ
(
z
∣
x
)
∣
∣
p
θ
(
z
∣
x
)
)
D_{KL}(q_{\phi}(z|x)||p_{\theta}(z|x))
DKL(qϕ(z∣x)∣∣pθ(z∣x))是估计的后验分布和真实分布的KL散度,我们希望最小化该KL散度(KL散度为0时两个分布没有差异),所以上述等式的左边就是联合建模的最大化优化目标,这等价于最大化等式的右边。这个等式的右边又称为Evidence lower bound,简称为ELBO,这主要是因为
p
θ
(
x
)
p_{\theta}(x)
pθ(x)一般称为evidence,而由于KL散度的非负性,所以有下述不等式:
l
o
g
p
θ
(
x
)
≥
E
z
q
ϕ
(
z
∣
x
)
l
o
g
p
θ
(
x
∣
z
)
−
D
K
L
(
q
ϕ
(
z
∣
x
)
∣
∣
p
θ
(
z
∣
x
)
)
log {p_{\theta}(x)} \ge E_{z~q_{\phi}(z|x)}logp_{\theta}(x|z) - D_{KL}(q_{\phi}(z|x)||p_{\theta}(z|x))
logpθ(x)≥Ez qϕ(z∣x)logpθ(x∣z)−DKL(qϕ(z∣x)∣∣pθ(z∣x))
所以ELBO是evidence的下限,ELBO是变分推断中经常用到的优化目标。对于VAE,ELBO取负就是其要最小化的训练目标:
L
V
A
E
(
θ
,
ϕ
)
=
−
E
z
q
ϕ
(
z
∣
x
)
l
o
g
p
θ
(
x
∣
z
)
+
D
K
L
(
q
ϕ
(
z
∣
x
)
∣
∣
p
θ
(
z
∣
x
)
)
θ
∗
,
ϕ
∗
=
a
r
g
min
θ
,
ϕ
L
V
A
E
\begin{aligned} L_{VAE}(\theta,\phi) &= - E_{z~q_{\phi}(z|x)}logp_{\theta}(x|z) + D_{KL}(q_{\phi}(z|x)||p_{\theta}(z|x)) \\ \theta^*,\phi^*&= arg\min_{\theta,\phi}L_{VAE} \end{aligned}
LVAE(θ,ϕ)θ∗,ϕ∗=−Ez qϕ(z∣x)logpθ(x∣z)+DKL(qϕ(z∣x)∣∣pθ(z∣x))=argθ,ϕminLVAE
对于优化目标的第二项,即计算
q
ϕ
(
z
∣
x
)
q_{\phi}(z|x)
qϕ(z∣x)和
p
θ
(
z
∣
x
)
p_{\theta}(z|x)
pθ(z∣x)的KL散度,首先我们必须要对两个分布做一定的假设:
q
ϕ
(
z
∣
x
)
=
N
(
z
;
μ
i
,
σ
2
i
I
)
p
θ
=
N
(
z
,
0
,
I
)
q_{\phi}(z|x) = N(z;\mu^i,\sigma^{2i}I) \\ p_{\theta} = N(z,0,I)
qϕ(z∣x)=N(z;μi,σ2iI)pθ=N(z,0,I)
即
q
ϕ
(
z
∣
x
)
q_{\phi}(z|x)
qϕ(z∣x)为各分量独立的多元高斯分布(协方差矩阵为对角矩阵),那么encoder网络预测的就是高斯分布的均值
μ
\mu
μ和方差
σ
2
\sigma^2
σ2(实际处理时预测
l
o
g
σ
2
log{\sigma^2}
logσ2,因为该值是无约束的)。而先验
p
θ
(
z
)
p_{\theta}(z)
pθ(z)为标准正态分布,这样就变成了计算两个多元高斯分布的KL散度。对于多元高斯分布,其概率密度函数为:
p
(
x
)
=
1
2
π
n
d
e
t
(
∑
)
e
x
p
−
1
2
(
x
−
μ
)
T
∑
−
1
(
x
−
μ
)
p(x) = \frac{1}{ \sqrt{{2\pi}^n}det(\sum)} exp{-\frac{1}{2}{(x-\mu)^T}\sum^{-1}(x-\mu)}
p(x)=2πndet(∑)1exp−21(x−μ)T∑−1(x−μ)
最终可以得到
q
ϕ
(
z
∣
x
)
q_{\phi}(z|x)
qϕ(z∣x)和
p
θ
(
z
∣
x
)
p_{\theta}(z|x)
pθ(z∣x)的KL散度:
K
L
(
D
K
L
(
q
ϕ
(
z
∣
x
)
∣
∣
p
θ
(
z
∣
x
)
)
)
=
K
L
(
N
(
z
;
μ
i
;
σ
2
i
I
)
∣
∣
N
(
z
,
0
,
I
)
)
=
1
2
(
t
r
(
σ
2
i
)
I
+
(
μ
i
)
T
μ
i
−
n
−
l
o
g
(
d
e
t
σ
2
i
I
)
=
1
2
∑
j
=
n
n
(
(
σ
2
i
)
2
+
(
μ
i
)
2
−
1
−
l
o
g
(
(
σ
2
i
)
2
)
)
\begin{aligned} KL(D_{KL}(q_{\phi}(z|x)||p_{\theta}(z|x))) &= KL(N(z;\mu^i;\sigma^{2i}I)||N(z,0,I))\\ &= \frac{1}{2}(tr(\sigma^{2i})I + (\mu^i)^T\mu^i -n -log(det\sigma^{2i}I)\\ &= \frac{1}{2}\sum^n_{j=n}((\sigma^{2i})^2 + (\mu^i)^2 -1 -log((\sigma^{2i})^2)) \end{aligned}
KL(DKL(qϕ(z∣x)∣∣pθ(z∣x)))=KL(N(z;μi;σ2iI)∣∣N(z,0,I))=21(tr(σ2i)I+(μi)Tμi−n−log(detσ2iI)=21j=n∑n((σ2i)2+(μi)2−1−log((σ2i)2))
现在我们来分析优化目标的第一项
−
E
z
q
ϕ
(
z
∣
x
)
l
o
g
p
θ
(
x
∣
z
)
- E_{z~q_{\phi}(z|x)}logp_{\theta}(x|z)
−Ez qϕ(z∣x)logpθ(x∣z),它一般被称为重建误差(reconstruction error),因为
l
o
g
p
θ
(
x
∣
z
)
logp_{\theta}(x|z)
logpθ(x∣z)正是给定
z
z
z下生成真实数据
x
x
x的似然(Likelihood)。对于一个给定的训练样本
x
i
x^i
xi,我们可以采蒙特卡洛方法(Monte Carlo method)来估计这个数学期望,即从
q
ϕ
(
z
∣
x
)
q_{\phi}(z|x)
qϕ(z∣x)多次采样来估计:
$$
- E_{z~q_{\phi}(z|x)}logp_{\theta}(x|z) \approx -\frac{1}{L}\sum_{l=1}^{L}(log(p_{\theta}(x|z)))
KaTeX parse error: Can't use function '$' in math mode at position 5: 这里的$̲L$为采样的总次数,实际上在具…
z \sim q_{\phi}(z|x) = N(z;\mu,\sigma^{2i} I)\
z = \mu + \sigma \odot \epsilon,where \epsilon \sim N(0,I)
$$
直观上讲,就是首先从标准正态分布随机采样一个样本,然后乘以encoder预测的标准差,再加上encoder预测的均值,这样就能计算该损失对encoder网络参数的梯度了。

根据建模的数据类型,
p
θ
(
x
∣
z
)
)
p_{\theta}(x|z))
pθ(x∣z))分布可以是一个高斯分布也可以是一个伯努利分布,这里以更通用的高斯分布为例。假定
p
θ
(
x
∣
z
)
)
p_{\theta}(x|z))
pθ(x∣z))分布也属于一个各分量独立的多元高斯分布:
p
θ
(
x
∣
z
)
=
N
(
z
;
μ
,
σ
2
i
I
)
p_{\theta}(x|z) = N(z;\mu,\sigma^{2i} I)
pθ(x∣z)=N(z;μ,σ2iI)。由于各个分量独立,所以我们可以单独计算每个分量:
l
o
g
p
θ
(
x
∣
z
)
=
l
o
g
1
2
π
σ
2
e
x
p
(
−
(
x
−
μ
)
2
2
σ
2
)
=
l
o
g
1
2
π
σ
2
−
1
2
σ
2
(
x
−
μ
)
2
\begin{aligned} logp_{\theta}(x|z) &= log \frac{1}{\sqrt{2\pi \sigma^2}}exp(-\frac{(x-\mu)^2}{2\sigma^2}) \\ &= log \frac{1}{\sqrt{2\pi \sigma^2}} - \frac{1}{2\sigma^2}(x-\mu)^2 \end{aligned}
logpθ(x∣z)=log2πσ21exp(−2σ2(x−μ)2)=log2πσ21−2σ21(x−μ)2
对于这个高斯分布的标准差,我们往往假定它是一个常量,而均值是由decoder预测得出:
μ
=
f
θ
(
z
)
\mu=f_{\theta}(z)
μ=fθ(z)。那么则有:
−
l
o
g
p
θ
(
x
i
∣
z
i
,
l
)
=
C
1
+
C
2
∑
d
D
(
x
d
i
−
(
f
θ
(
z
i
,
l
)
)
d
)
2
-logp_{\theta}(x^i|z^{i,l}) = C_1 + C_2\sum_d^D(x_d^i - (f_{\theta}(z^{i,l}))d)^2
−logpθ(xi∣zi,l)=C1+C2d∑D(xdi−(fθ(zi,l))d)2
这里
C
1
C_1
C1和
C
2
C_2
C2均是常量,而D是变量x的维度大小。如果忽略常量
C
1
C_1
C1的话,那么重建误差其实就是L2损失。上面我们是假定
p
θ
(
x
∣
z
)
p_{\theta}(x|z)
pθ(x∣z)分布是一个高斯分布,如果
p
θ
(
x
∣
z
)
p_{\theta}(x|z)
pθ(x∣z)是一个伯努利分布即0-1分布的话,此时decoder直接预测概率值(sigmoid激活函数),重建误差就是交叉熵:
l
o
g
p
θ
(
x
∣
z
)
=
∑
d
D
(
x
d
l
o
g
(
f
θ
(
z
)
d
)
+
(
1
−
x
)
l
o
g
(
1
−
f
θ
(
z
)
d
)
)
logp_{\theta}(x|z) = \sum^D_d(x_dlog(f_{\theta}(z)_d) + (1-x)log(1-f_{\theta}(z)_d))
logpθ(x∣z)=d∑D(xdlog(fθ(z)d)+(1−x)log(1−fθ(z)d))
根据上述分析,对给定的一个训练样本
x
i
x_i
xi,其训练损失(假定是高斯分布)为:
L
V
A
E
(
θ
,
ϕ
,
x
i
)
=
−
E
z
∼
q
ϕ
(
z
∣
x
i
)
l
o
g
p
θ
(
x
i
∣
z
)
+
D
K
L
(
q
ϕ
(
z
∣
x
i
)
∣
∣
p
θ
(
z
)
)
=
C
L
∑
l
=
0
L
∑
d
=
0
D
(
x
d
−
(
f
θ
(
z
i
,
l
)
)
d
)
2
+
1
2
∑
j
=
0
n
(
(
σ
j
i
)
2
+
(
μ
j
i
)
2
−
1
−
l
o
g
(
(
σ
j
i
)
2
)
)
\begin{aligned} L_VAE(\theta,\phi,x^i) &= -E_{z \sim q_{\phi}(z|x^i)}log p_{\theta}(x^i|z) + D_{KL}(q_{\phi}(z|x^i)||p_{\theta}(z))\\ &= \frac{C}{L}\sum^L_{l=0}\sum^D_{d=0}(x_d -(f_{\theta}(z^{i,l}))d)^2 + \frac{1}{2}\sum_{j=0}^n( (\sigma_j^i)^2 + (\mu_j^i)^2 -1 - log((\sigma_j^i)^2)) \end{aligned}
LVAE(θ,ϕ,xi)=−Ez∼qϕ(z∣xi)logpθ(xi∣z)+DKL(qϕ(z∣xi)∣∣pθ(z))=LCl=0∑Ld=0∑D(xd−(fθ(zi,l))d)2+21j=0∑n((σji)2+(μji)2−1−log((σji)2))
如果把KL散度项看到一个正则化的话,那么VAE的损失函数就是重建误差+正则化,这样VAE就可以看成是一个加了约束的AE。VAE的整个训练流程如下所示:输入x,encoder首先计算出后验分布的均值和标准差,然后通过重采样方法采样得到隐变量z,然后送入decoder得到重建的数据x′。
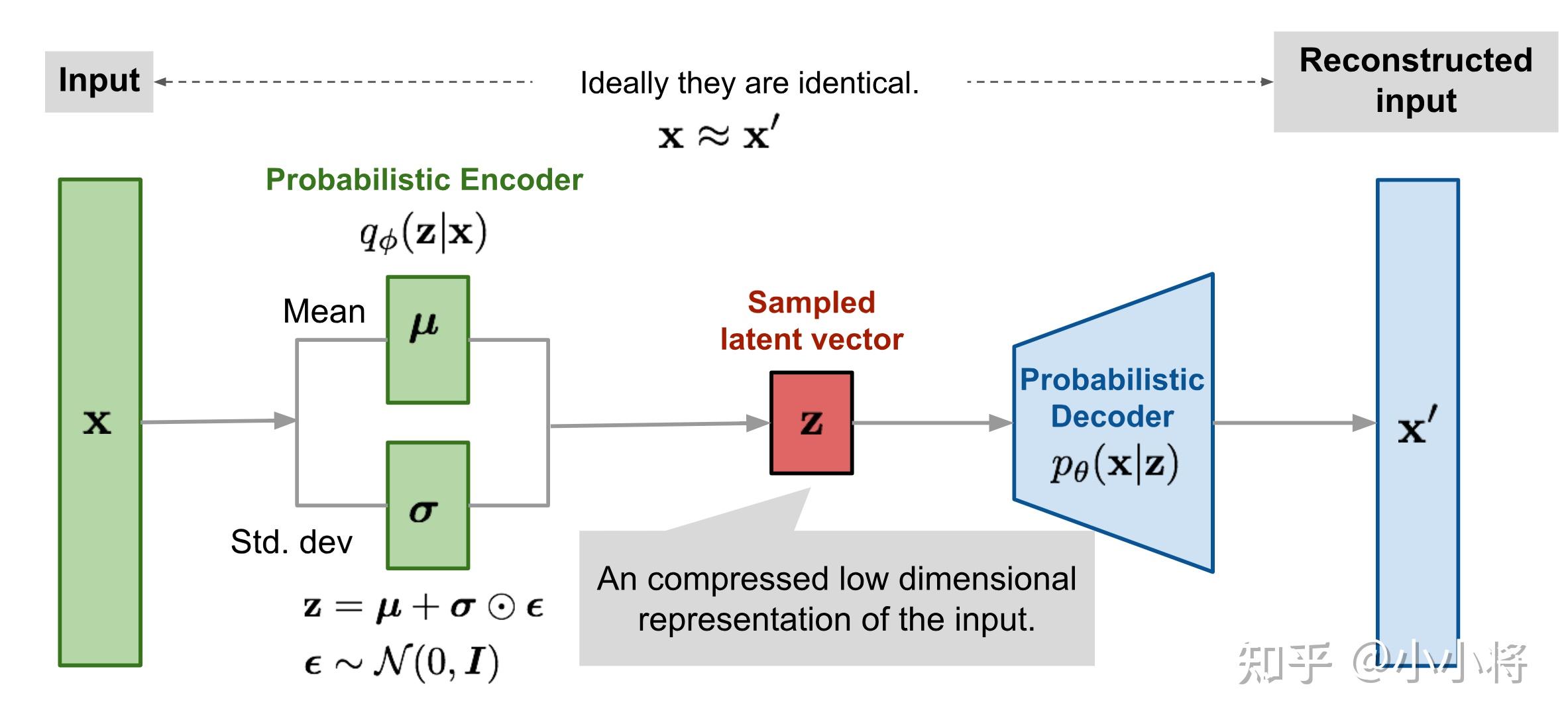
训练完成后,我们就得到生成模型 p θ ( x ∣ z ) p θ ( z ) p_{\theta}(x|z)p_{\theta}(z) pθ(x∣z)pθ(z),其中 p θ ( x ∣ z ) p_{\theta}(x|z) pθ(x∣z)就是decoder网络,而先验$ p_{\theta}(z) 为标准正态分布,我们从 为标准正态分布,我们从 为标准正态分布,我们从p_{\theta}(z)$随机采样一个z,送入decoder网络,就能生成与训练数据X类似的样本。
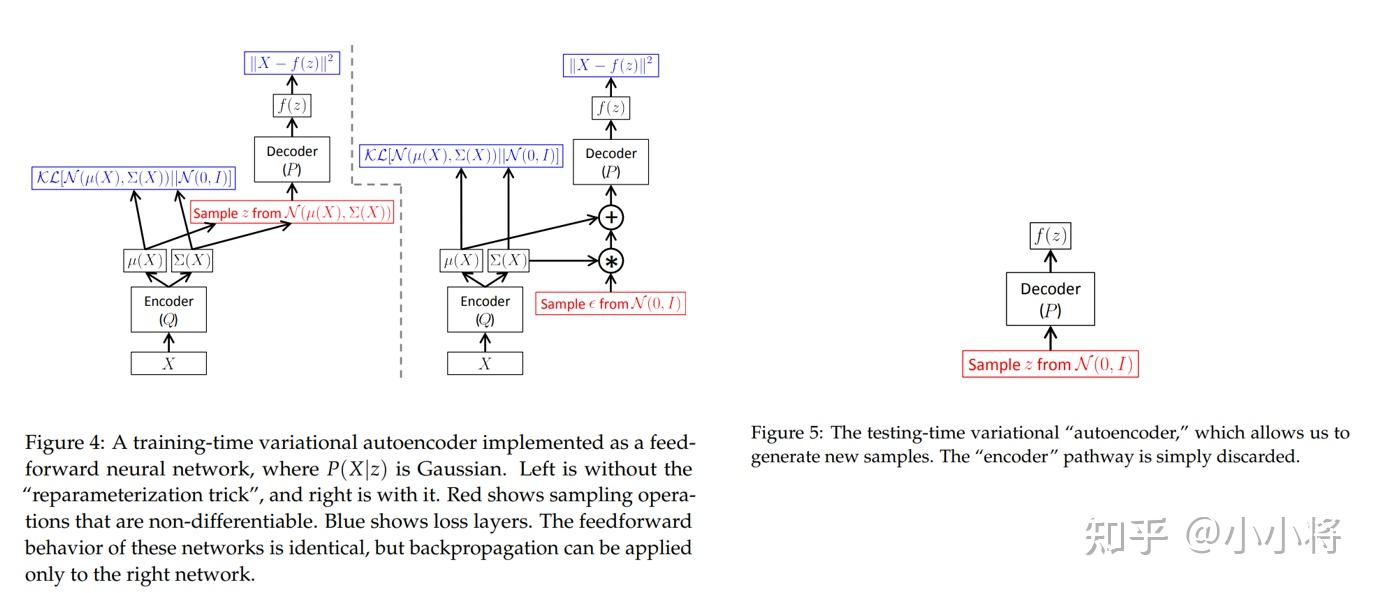
3.2 StableDiffusion
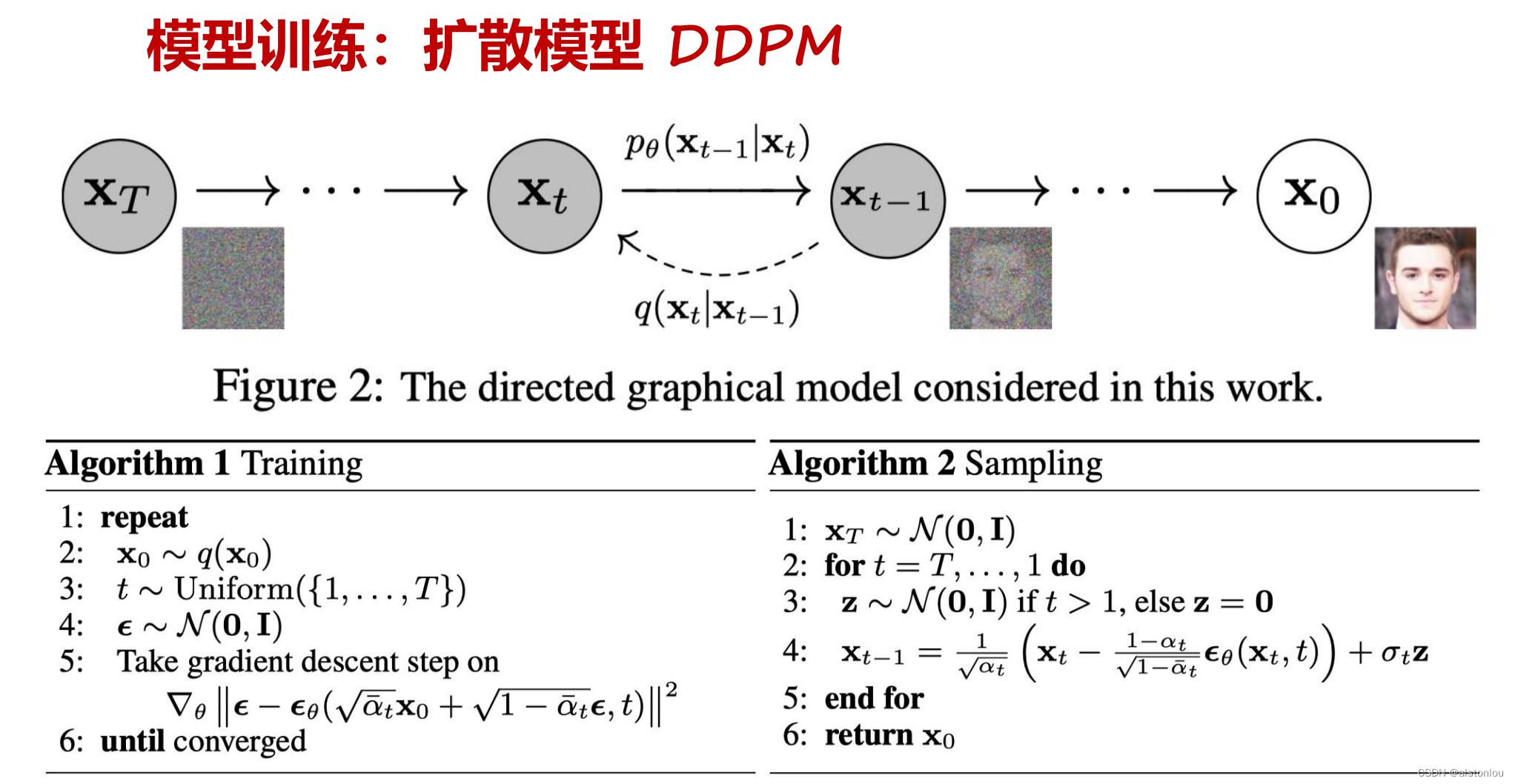
3.3 Scaling Transformers
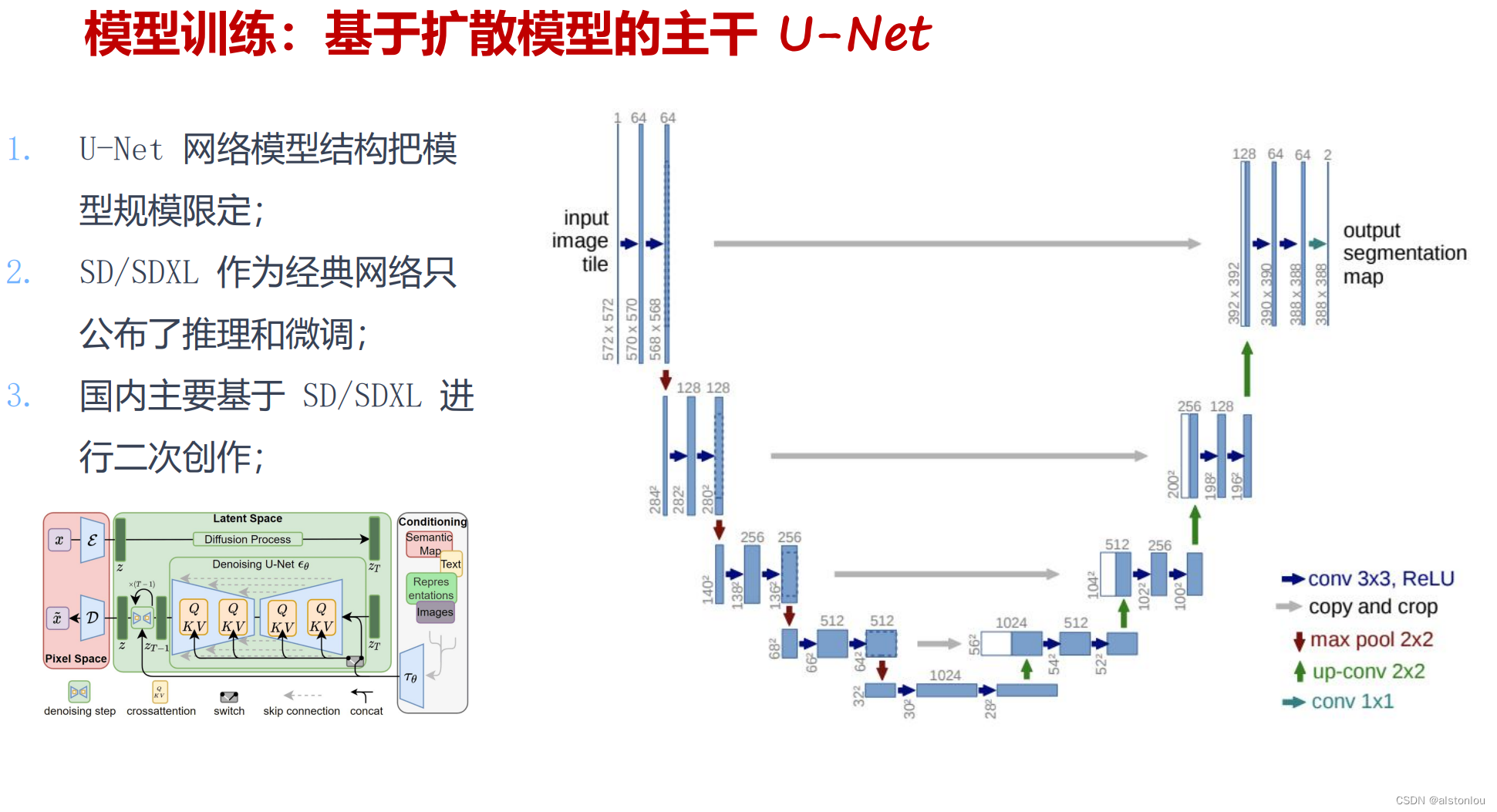

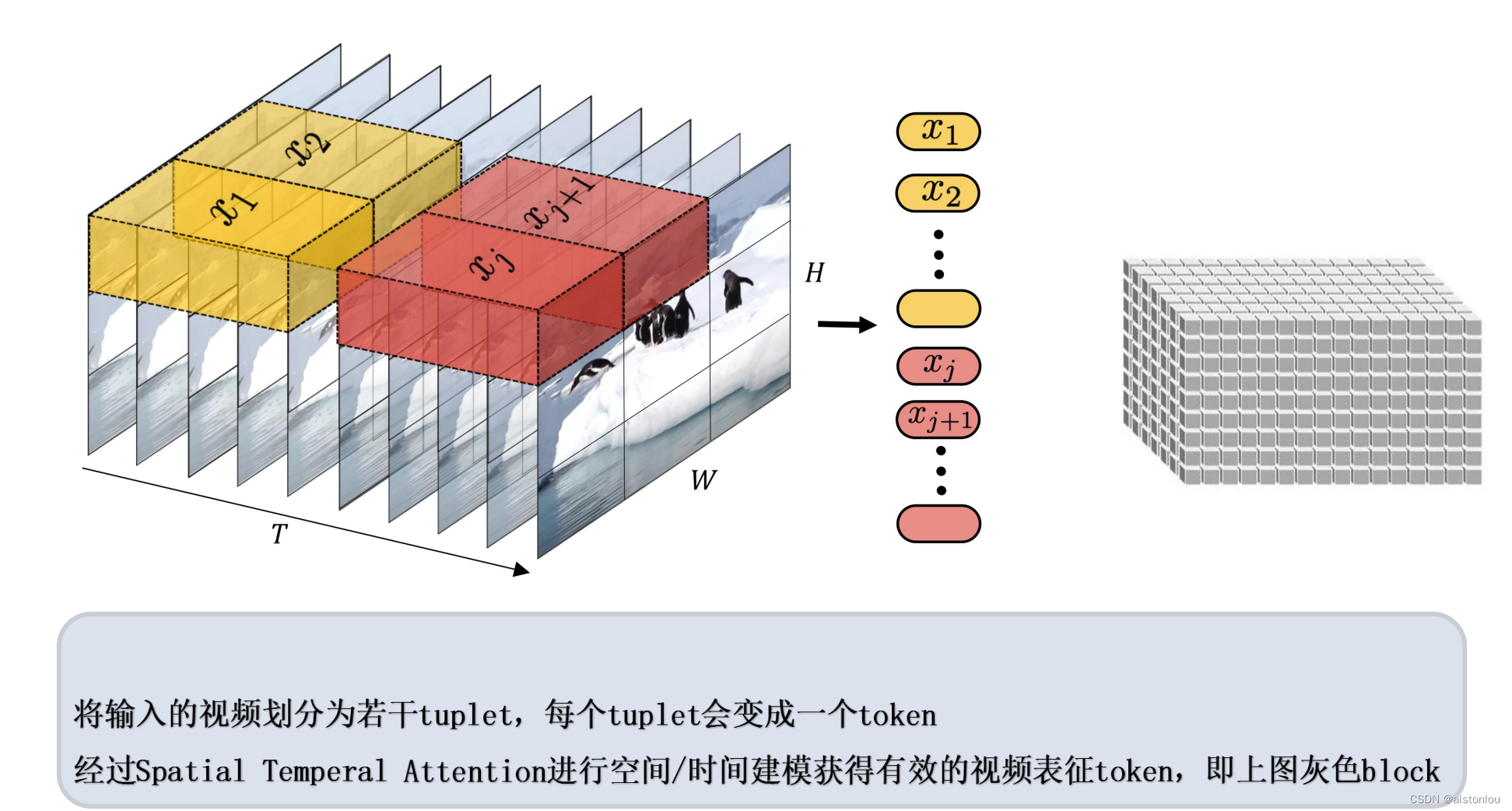
3.4 patches模块
视频由多帧的图片组成,因此,一个视频文件是本质上是包含了时间维度的三维图片数据。

因此,对数据进行patches进行打包方法其实有两种:
- 摊大饼法:从输入视频剪辑中均匀采样 n_t 个帧,使用与ViT 相同的方法独立地嵌入每个2D帧(embed each 2D frame independently using the same method as ViT),并将所有这些 token连接在一起

- 切面包法:
四、具体的工程难点
通过上面的技术讲解,已经基本涵括了本次sora模型中最为基础的模型框架,但依旧存在一些不知道的问题工程细节问题:
视频压缩网络的压缩率是多少,Encoder中的复杂度是具体怎么设置的,时空patches中排布的方法等。
参考
生成模型之VAE:https://zhuanlan.zhihu.com/p/452743042
sora技术参考:https://github.com/datawhalechina/sora-tutorial/tree/main/docs




























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










