基于多目标的进化约束多目标优化约束处理技术：一种新视角

个人学习用，如若侵权，请联系我，删除此文。

原文请引用：

Z. -Z. Liu, Y. Qin, W. Song, J. Zhang and K. Li, "Multiobjective-Based Constraint-Handling Technique for Evolutionary Constrained Multiobjective Optimization: A New Perspective," in IEEE Transactions on Evolutionary Computation, vol. 27, no. 5, pp. 1370-1384, Oct. 2023, doi: 10.1109/TEVC.2022.3194729.

这篇文章主要是将约束多目标优化问题转换为多目标优化问题进行求解，即：将（1）转换为了（4），CV是约束违反程度，求解（1）就是寻找，CV和F都小的解。

这篇文章将转换后的问题（4）的Pareto解集，定义为TPS，将原始问题（1）的Pareto解集定义为CPS，（1）若是没有后面约束的Pareto解集，定义为UPS。满足如下两个关系：

①CPS是TPS的可行子集。

②CPS中不存在Pareto支配TPS中的解。

定义：TPS中不支配其他解的解为边界解（BFS）

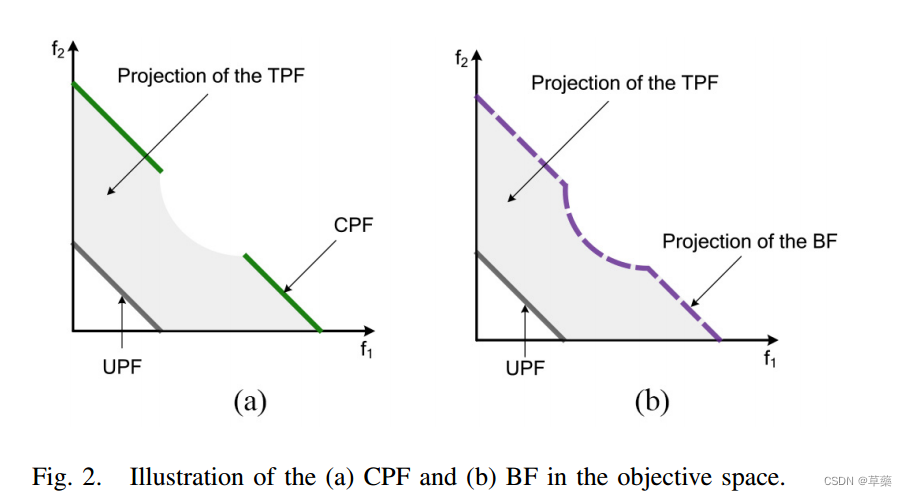
根据①和②得出结论：CPS是BFS的可行子集，BFS是TPS的可行子集。所以，求解CMOP的过程可以先求TPS，再求BFS，最后求CPS。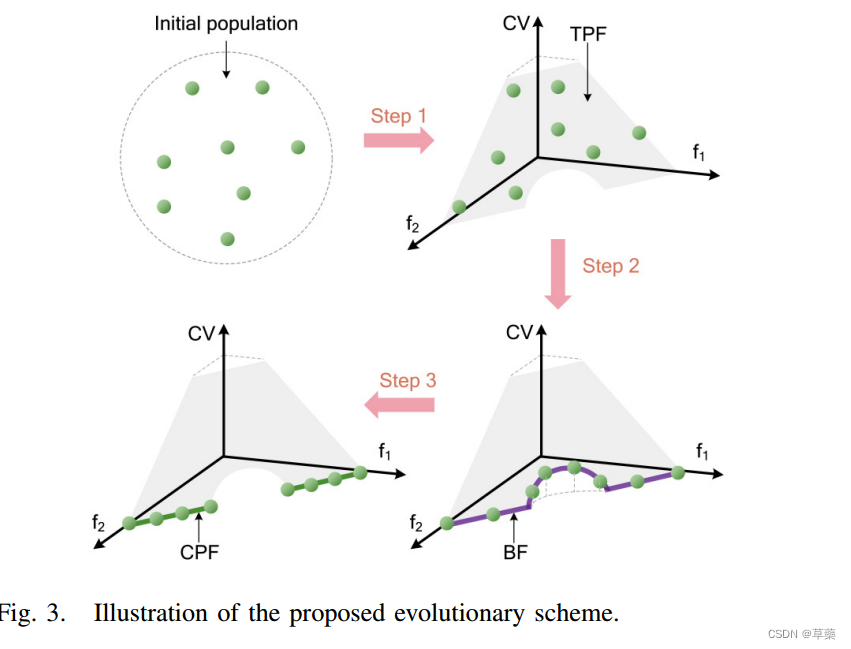

提出NRC算法

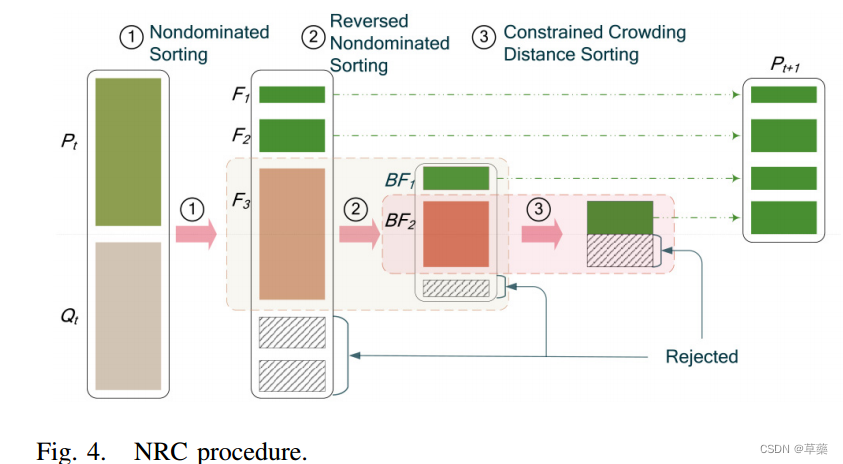
解释一下，结合上图：先求TPS，利用转换后的问题（4），非支配排序，得到分层，F1，F2，，，（这些F里绿色的是最后得到的下一代的解）这里的F分几层进入到下一代和种群规模有关，要大于种群规模，之后将最后一层能进入到下一代的分层F，对目标空间进行反非支配排序，得到BF1,BF2,,,,（因为这里的BF是边界解，不支配TPS中的其他解，所以在F层里要得到不支配其他的解，就用了反向非支配排序，就是对每个目标函数都取负号，然后用支配排序），最后对分层的BF，前面的进入下一代（绿色的），剩下的利用约束拥挤度距离进行排序（兼顾多样性和可行性）进入下一代。
这样实现了，先找TPS，再找BFS，最后找CPS。

最大疑问：

1.这里的分层不知道是否一定能保证，F1，F2，，，他们的CV是0，后面的F一定是BF吗？

2.后面的NCR2还没细看，存档

接下来看NCR2

NCR是利用不可行性进行辅助，善于多样性；CDP是可行性驱动，善于将种群引导至可行区域。

NCR2=NCR+CDP双存档     可行性存档FA 不可行存档IA

NCR2包括FA和IA的更新，以及后代生成

①更新FA（利用CDP）：后代和FA，可行解数量>N，非支配排序+拥挤度距离排序选N个；若数量不足N，从不可行解中选CV小的进行找补。

②更新IA（利用NCR）：仅用不可行解进行更新。在变换后的目标空间中对IA,FA和后代使用非支配排序，分层，选可行解和不可行解，若分层的不可行解数量>N，利用反支配排序和拥挤度距离排序选N个不可行解，进行截断。（这里的拥挤度距离不利用CV）

③后代生成：利用IA和FA精英信息生成后代，考虑以下两种情况。
  1）if FA 中可行解<N，或IA<N，则根据决策空间中的密度值选择父代。
       具体来说，它首先从 FA 和 IA 的联合种群中随机挑选两个解。然后，选择决策空间中密度值较小的解作为父代解。

  2）else 以锦标赛方式从FA和IA中选父代，概率分别为alpha和1-alpha。

       FA锦标赛选择中采用Pareto支配和目标空间密度，IA采用反向非支配和目标空间密度。

最后笔者个人总结一下：这个NCR2采用的思想就是双存档，有很多其他的双存档方法求解CMOP，但是我没有细看，这篇思想是一个可行解存档和一个不可行解存档，可行解存档采用CDP，以保留可行解为主，不可行解存档是采用的这篇文章提出的NCR，就是在不可行解中寻找可行以及极有可能成为可行的解，实现最后的CMOP，把这些保留下来的精英解（FA中有可行的，IA中有有可能以后成为可行的优良解），保证了解的多样性和可行性，利用这两个存档的交配生成后代。这里的不可行存档研究比较有意思，也解决了我个人的第一个疑问。这里的交配我没有细研究，还是存档