基本概念
个体(染色体):一个个体就是一条染色体。一个个体通常代表待求解问题的一个可行解,常用一串数字表示,数字串中的一位对应一个基因。
种群:个体的集合。集合内的个体数称为种群大小。
种群大小 M:一般10<M<200。
交叉概率 Pc:Pc越大,算法在搜索区域的搜索能力越强。Pc取得过大,算法收敛速度慢;Pc取得过小,算法容易陷入局部最优点。一般0.4<Pc<1。
变异概率Pm:Pm过大,容易丢失最优解,甚至使算法趋于纯粹的随机搜索。Pm过小,可能使算法过早地收敛于局部最优点。通常0.005<Pm<0.1
选择算子:优良基因能够有更多机会被遗传复制到下一代。常用的选择算子有轮盘赌选择、排序选择、锦标赛选择、精英保留选择、随机竞争选择。
算法基本思想
初始阶段,遗传算法将问题解转化成一串编码,从一组随机产生的表示问题解的编码初始群体开始搜索,以根据问题特征确定的适应度函数为依据,使用选择策略在当前种群中选择个体,通过交叉和变异来产生下一代种群。如此模仿生命的进化过程一代代演化下去,直到满足期望的终止条件或进化到一定代数为止。
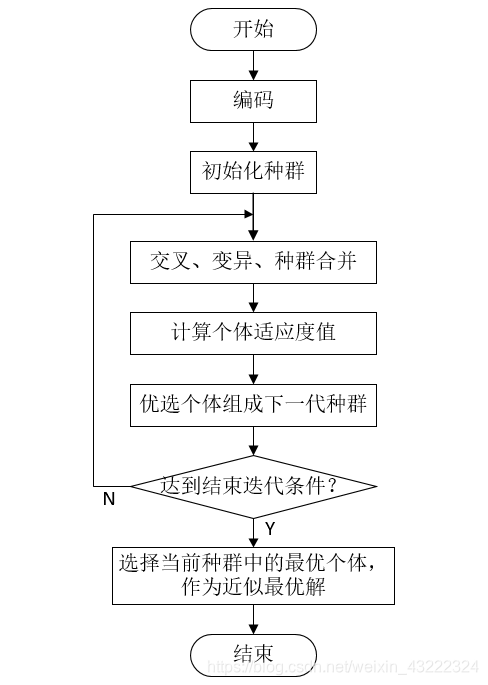
- 第一步,编码。对个体进行编码,根据实际问题选择编码方式,例如二进制编码、十进制编码。个体记为T。
- 第二步,初始化种群。种群大小设为M,种群初始化为P=[T1,T2,……,TM]。初始化交叉概率为Pc,变异概率为Pm。
- 第三步,交叉、变异、种群合并。对种群进行交叉、变异处理,在进行交叉操作时先打乱种群个体顺序,种群以概率Pc进行交叉,以概率Pm进行变异。交叉变异后的子种群记为Q。合并原种群P和子种群Q,合并种群记为C,C=P∪Q。合并种群C中的个体数目为2M。
- 第四步,计算个体适应度值,优选个体组成下一代种群。 针对待求问题的目标确定相应适应度函数,用适应度函数对个体的适应度值进行计算,适应度值记为F。然后采用选择算子,得到下一代种群。
- 第五步,最后判断是否达到迭代结束条件。 如果是,进入第六步,否则进入第三步。
- 第六步,选择当前种群中的最优个体,作为近似最优解。
选择算子
一、轮盘赌选择法(赌轮选择法)
比例选择方法,个体被选择的概率与其适应度值大小成正比。种群中的所有个体按照其适应度值占总适应度值的比例组成面积为1的一个圆盘,指针停止转动后,指向的个体将被复制到下一代适应度值越大的个体越容易被选中。
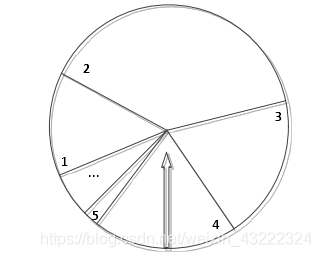
Pi=Fi/(F1+…+Fi…+Fn),Fi是第i个个体的适应度值
PPi=P1+……+Pi,PPi是累计概率
转轮时,产生一个0~1之间的随机数r,当PPi-1<=r<PPi时,就选择第i个个体。
二、锦标赛选择法
打乱合并种群C中个体的顺序,通过两两比较适应度值F,保留F值大的个体,淘汰F值小的个体,得到下一代种群。
一个最最简单的例子
例子:用遗传算法求出最大的5位二进制数。
问题过于简单,请各位不要嫌弃,这个问题只是为了举例。
分析
显然,最大的5位二进制数是11111,这个我们都知道,如何用遗传算法求出最大的5位二进制数呢?
首先根据问题确定个体编码方式、适应度函数等。
- 个体:5位二进制数,例如00010、10101、01001……
- 编码方式:肯定是二进制编码
- 种群大小、交叉概率、变异概率:这些都是根据经验设置的,这里种群大小M=50,交叉概率Pc=1,变异概率Pm=0.01。
- 选择算子:就用锦标赛选择法吧,但是用其他的也行。打乱合并种群C中个体的顺序,通过两两比较适应度值F,保留F值大的个体,淘汰F值小的个体,得到下一代种群。
- 适应度函数:F=16*a4 + 8*a3 + 4*a2 + 2*a1 + a0,a4是5位二进制数的最高位,依次类推,a0是最低位。一个个体的适应度值就是这个二进制数本身的大小,例如个体“00000”的适应度值F=0,个体“11111”的适应度值F=31,这个二进制数越大,适应度值越大,越有可能遗传复制到下一代。
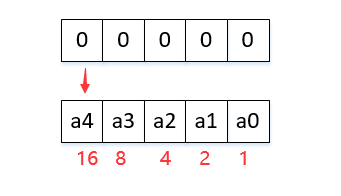
图解整个过程
编码。上面分析里已经编过了,每个个体都是一串5位二进制数
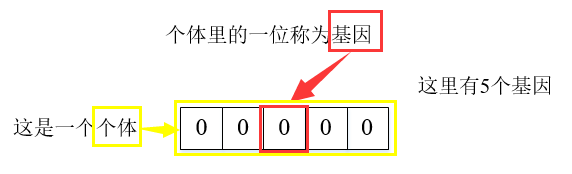
初始化种群。随机生成50个 5位二进制数,这50个个体作为初始种群。

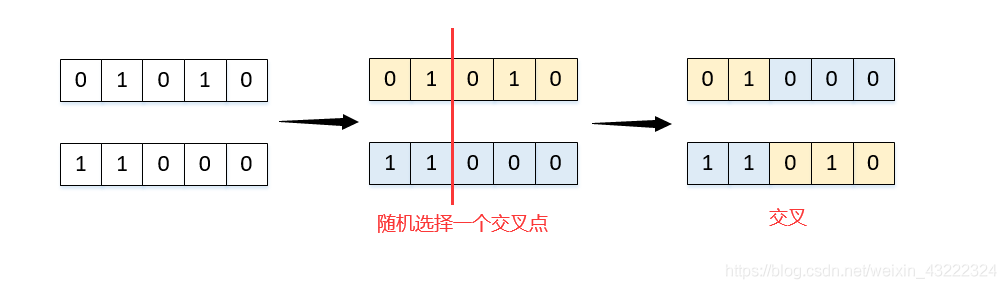
交叉。 种群共有50个个体,先随机打乱这50个个体的顺序,然后1号个体和2号个体交叉,得到两个新的个体,如图所示,再3号和4号个体交叉,以此类推。最后,父代种群50个旧个体经过两两交叉,就能得到50个新个体。
种群以概率Pc进行交叉的程序实现:随机生成一个0~1之间的数p,如果p<=交叉概率Pc,进行交叉操作,否则不进行交叉操作。
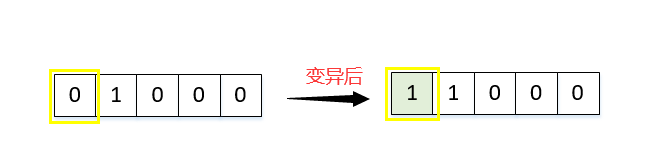
变异。 对上一步得到的交叉后的50个新个体的每位基因进行遍历,从第1个个体的第1位基因开始,以概率Pm进行变异,随机生成一个0~1之间的数p,如果p<=变异概率Pm,该位基因进行变异操作,否则不进行变异操作。二进制编码方式的变异很简单,就是直接取反。以下是某个体的某个基因变异示意图:
种群合并。交叉变异后的子种群记为Q(也就是50个新个体)。合并原种群P(也就是原来50个旧个体)和子种群Q,合并种群记为C,C=P∪Q。合并种群C中的个体数目为100个(包含50个旧个体和50个新个体,新个体是由旧个体交叉变异得来的)。
计算个体适应度值,优选个体组成下一代种群。打乱合并种群C中个体的顺序,通过两两比较适应度值F,保留F值大的个体,淘汰F值小的个体,得到下一代种群。得到下一代种群。
在下图可以看到,F=10的个体 与 F=24的个体比较,F=10的个体被淘汰,F=24的个体被留下来了,合并种群中的100个个体这样两两比较,最后留下来50个个体,这50个个体的适应度值都较大。
这是一次迭代,这50个个体再作为父代种群拿去交叉变异又能得到100个个体,再从100个个体中选50个适应度较大的个体,接着循环这些步骤。每次进化(迭代),适应度值大的个体留下来了,一直迭代,最后种群中适应度大的个体就越来越多。

判断是否达到迭代结束条件。 个体11111被保留下来的概率很大,随着迭代,种群中为11111的个体越来越多,最后,种群中可能90%甚至更多的个体都是11111,当种群中相同的个体达到一定百分比时,可以结束迭代,选出种群中适应度最大的个体,那就是我们求的近似最优解了 。
本例的MATLAB程序
主程序 main.m
%% 用遗传算法求最大的5位二进制数
% date 2021/05/25 ; code by Wang Yuan
% input:无
% output:最大的5位二进制数
%% 清空环境变量
clc
clear
close all;
%% 初始化
dim=5; % 个体包含5位基因
popsize = 50; % 种群大小
genmax = 50; % 最大迭代次数
Pm = 0.01; % 变异概率
Pc = 1; % 交叉概率
% expect_fit = ; % 期望的适应度值,大于该值时结束迭代
Parents = round(rand(popsize,dim)); %随机生成初始种群,popsize个个体,先得到随机数后四舍五入
%% 以下这两是拿来画图用的
every_generation_fitness = zeros(1, genmax+1); % 保存每一代的个体平均适应度值
repeat_num_all = zeros(1, genmax); % 每一代种群中重复个体的数量
current_generation_fitness = zeros(1,popsize);
for g = 1 : popsize
current_generation_fitness(g) = fun_fitness(Parents(g







 基本思想 遗传算法首先将问题解转换成一组编码,并通过对编码进行选择、遗传和交叉变异的操作来找到最优解。
基本思想 遗传算法首先将问题解转换成一组编码,并通过对编码进行选择、遗传和交叉变异的操作来找到最优解。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章















 1573
1573











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








