递归算法 基础总结（斐波那契）（进制转换）（辗转相除法）（汉诺塔总结）（hdu2032杨辉三角）

递归的概念：

递归就是某个函数直接或间接调用自身的问题求解过程。
通过将自身问题划分成相同性质的子问题的求解过程，这些小问题的求解过程较容易，小问题的解就构成了原问题的解。

递归的设计思路：

要解决一个规模为n的问题，先看规模为n-1（或者n-k或者n/2，总之是比原问题规模小）的问题是否和原问题有同样的性质，如果性质相同，那这个问题应该可以用递归算法解决

特点：

1，递归就是在函数里或过程中调用自身。
2，在递归过程中必须有一个明确的结束条件，即递归出口。
3，递归解题简介，递归效率不高，但是代码不多。一般不提倡用递归。
4，递归时系统为每一层的返回点，局部变量，提供栈来存储。递归次数多了，容易发生栈溢出。

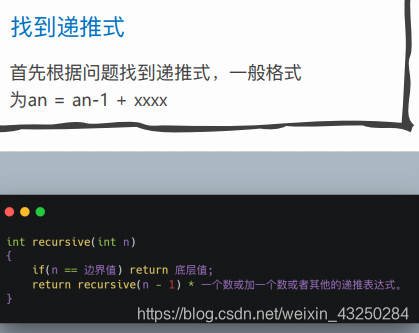
关键

1.找出递推关系式
2.找到递归终止条件
注：深层次的递归可能导致栈溢出，可以考虑使用全局数组或动态分配数组

举例：

1：求n的阶乘

递推关系式 f(x)=x*f(x-1)
终止条件 乘到1后，x-1=0,结束递归返回1

#include<stdio.h>
long long int f(int x)
{
    if(x==0)
        return 1;
    else
        return x*f(x-1);
}
int main()
{
    int n;
    scanf("%d",&n);
    long long int ans=f(n);
    printf("%lld",ans);
    return 0;
}

2：斐波那契递归

基本定义
斐波那契数列指的是这样一个数列 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233，377，610，987，1597，2584，4181，6765，10946，17711，28657，46368…

斐波那契数列
特别指出：第0项是0，第1项是第一个1。
这个数列从第3项开始，每一项都等于前两项之和。

一般思路：f(n)=f(n-1)+f(n-2)

int fabonacci(int n)
{
    if(n <0)
    	return -1;
    else if(n==0)
    	return 0;
    else if(n==1)
    	return 1;
    else
    	return fabonacci(n)+fabonacci(n-1);
 }

与改进后思路的对比：

#include<stdio.h>

int n1 = 0;//记录普通的递归次数
int n2 = 0;//优化的递归次数

//普通递归函数
int fibon(int n)
{
	n1 ++;
	if(n <= 2)//递归出口
	{
		return 1;
	}
	return fibon(n-1) + fibon(n-2);
}

//优化后的递归函数
int fibonac(int a,int b,int n)
{
	n2 ++;
	if(n > 2)
	{
		return fibonac(a+b,a,n-1);
	}
	return a;
}
int main()
{
	int n = 10;//第几个斐波那契数列

	int a = 1; //斐波那契数列的第一项
	int b = 1;//第二项

	int i = fibon(n);//普通的递归
	int j = fibonac(a,b,n);//优化后的递归

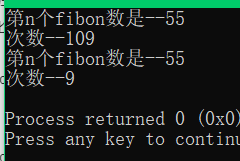
	printf("第n个fibon数是--%d\n",i);
	printf("次数--%d\n",n1);

	printf("第n个fibon数是--%d\n",j);
	printf("次数--%d\n",n2);

	return 0;
}

对比一下：

3：将任意十进制转换为K(1<k<10)进制

Input
第一行输入一个数n，表示n（0<n<=100）组测试数据
接下来的n行每一行输入一个数 m和k表示将m转化为相应的进制表示
(0<m<100000000)

Output
输出转化完成后的数

Sample Input
2
9 7
13 3
Sample Output
12
111

AC代码：

#include <bits/stdc++.h>
using namespace std;
void han(int m,int k)
{
    if(m/k!=0)
    {
        han(m/k,k);                
        printf("%d",m%k);
    }
    else
        printf("%d",m);
}
int main()
{
    int n;
    cin>>n;
    while(n--)
    {
        int m,k;
        cin>>m>>k;
        han(m,k);
        printf("\n");
    }
    return 0;
}

顺便总结一下模板：一个十进制数m转化成k（k<10)进制

void han(int m,int k)
{
    if(m/k!=0)
    {
        han(m/k,k);               
        printf("%d",m%k);
    }
    else
        printf("%d",m);
}

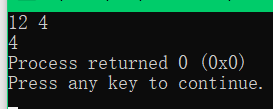
4：递归法的应用：辗转相除法求最大公约数：

#include <bits/stdc++.h>
using namespace std;
int gcd(int a,int b)
{
    if(a%b==0)
        return b;
    else
        return gcd(b,a%b);
}
int main()
{
    int a,b;
    scanf("%d%d",&a,&b);
    printf("%d",gcd(a,b));
    return 0;
}

5： 汉诺塔问题总结：

汉诺塔（又称河内塔）问题是源于印度一个古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上安大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，在小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘。

首先，递归的组成有两部分，一个是递归体，一个是递归结束条件。 其本质在于重复 ，因此找到了重复的内容就能推导出递归体。

对此汉诺塔题目来说，将三个柱子(初始柱，过渡柱，目标柱)分别标记为x，y，z（注：这里的柱子相当于实参，字母相当于形参）

这个搬圆盘活动抽象后可分成三步：

1. 将初始柱上除最下面的圆盘以外的圆盘全部搬到过渡柱上；就是把n-1个圆盘从x柱子移到y柱子上去。就是han(n-1,x,z,y);
2. .将初始柱上最下面的圆盘搬到目标柱上； 就是printf("%c–>%c\n",x,z);
3. 将过渡柱上的圆盘全部搬到目标柱上。 这一步也可以看做是第一步的逆向操作。就是han(n-1,y,x,z);

一切搬圆盘都是在重复上面三个步骤，因此，这三步便是一个递归体。

汉诺塔问题源于印度神话
那么好多人会问64个圆盘移动到底会花多少时间？那么古代印度距离现在已经很远，这64个圆盘还没移动完么？我们来通过计算来看看要完成这个任务到底要多少时间？
我们首先利用数学上的数列知识来看看
F(n=1)=1,F(n=2)=3,F(n=3)=7,F(n=4)=15……F(n)=2F(n-1)+1;
我们使用数学归纳法可以得出
计算时间的通项式：F(n)等于2ⁿ-1。
当n为64时F(n=64)=18446744073709551615。
我们假设移动一次圆盘为一秒，那么一年为31536000秒。那么18446744073709551615/31536000约等于584942417355天，换算成年为5845.54亿年。
目前太阳寿命约为50亿年，太阳的完整寿命大约100亿年。所以我们整个人类文明都等不到移动完整圆盘的那一天。。。

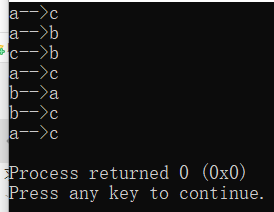
写一下移动过程：

其中han(3,‘a’,‘b’,‘c’)；表示一共3个盘子，初始时全在a柱上，要经过b这个过度柱子，全把盘子移动到c柱子上去。

#include <bits/stdc++.h>
using namespace std;
int han(int n,char x,char y,char z)
{
    if(n==1)
        printf("%c-->%c\n",x,z);
    else
    {
        han(n-1,x,z,y);
        printf("%c-->%c\n",x,z);
        han(n-1,y,x,z);
    }
}
int main()
{
    han(3,'a','b','c');//3个盘子的话
    return 0;
}

hdu2032杨辉三角

Problem Description
还记得中学时候学过的杨辉三角吗？具体的定义这里不再描述，你可以参考以下的图形：
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
Input
输入数据包含多个测试实例，每个测试实例的输入只包含一个正整数n（1<=n<=30），表示将要输出的杨辉三角的层数。
Output
对应于每一个输入，请输出相应层数的杨辉三角，每一层的整数之间用一个空格隔开，每一个杨辉三角后面加一个空行。
Sample Input
2 3
Sample Output
1
1 1

1
1 1
1 2 1

#include<stdio.h>
int main()
{
    int I[32][32]={0};
    for(int i=0;i<31;i++)
        I[i][0]=1;
    for(int i=1;i<31;i++)
    {
        for(int j=1;j<=i;j++)
            I[i][j]=I[i-1][j-1]+I[i-1][j];
    }
    int n;
    while(scanf("%d",&n)!=EOF)
    {
        for(int i=0;i<n;i++)
        {
            for(int j=0;j<=i;j++)
            {
                printf("%d",I[i][j]);
                if(j!=i)printf(" ");
                if(j==i)printf("\n");
            }
        }
        printf("\n");
    }
    return 0;
}