傅里叶变换概述

        ​​​​​​​知识补充：

        1.时域与频域：

                1）时域（时间域）——自变量是时间，即横轴是时间，纵轴是信号的变化。其动态信号时描述信号在不同时刻取值的函数。

                2）频域（频率域）——自变量是频率，即横轴是频率，纵轴是该频率信号的幅度，也就是通常所说的频谱图。

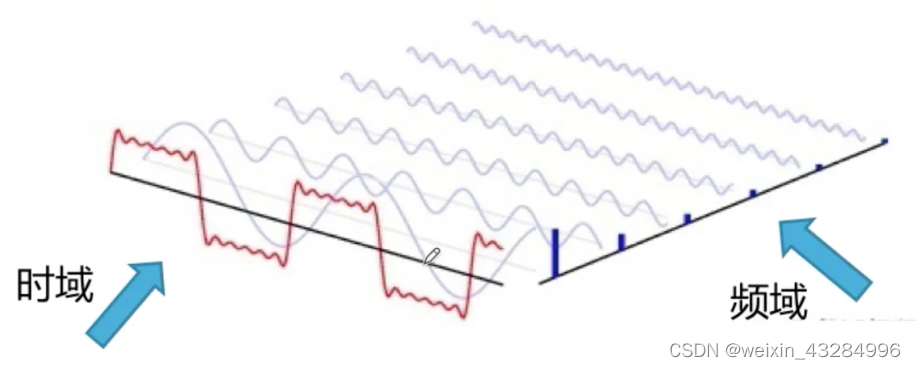
                3）频域与时域本身就是对称的，存在相互的制约关系：时域的连续信号对应频域的非周期，离散对应周期；时域的周期对应频域的离散，非周期对应连续。 

1.傅里叶级数（Fourier series，FS）

        连续、周期信号 --> 非周期、离散

         任何周期函数都可以用正弦函数和余弦函数构成的无穷级数来表示（选择正弦函数与余弦函数作为基函数是因为它们是正交的），后世称傅里叶级数为一种特殊的三角级数，根据欧拉公式，三角函数又能化成指数形式，也称傅里叶级数为一种指数级数。

        

        上式称为函数的正交展开式，也称为广义傅里叶级数。