Energy-based PINN在固体力学中的运用

简介

物理信息神经网络（Physic informed neural network，PINN）已经成为在有限差分、有限体积和有限元之后的另一种求解偏微分方程组的范式，受到学者们广泛关注。

在固体力学领域有两类不同的PINN:
（1）PDE-based method: 第一类使用神经网络表示位移场，将控制方程的残差直接引入神经网络的损失函数，通过梯度下降算法优化神经网络的权重和偏置，最终使得方程残差最小
（2）Energy-based method: 第二类使用神经网络表示位移场，将结构的总势能引入神经网络的损失函数，通过梯度下降算法优化神经网络的权重和偏置，最终使得结构的总势能最小。这种方法又被称为“深度里兹法”¹，体现的是最小势能原理，可以参见变分原理与泛函分析教程。

二者在理论上是等价的，但是Energy-based方法在数学上更加直接，所以这里重点介绍第二类方法。

神经网络

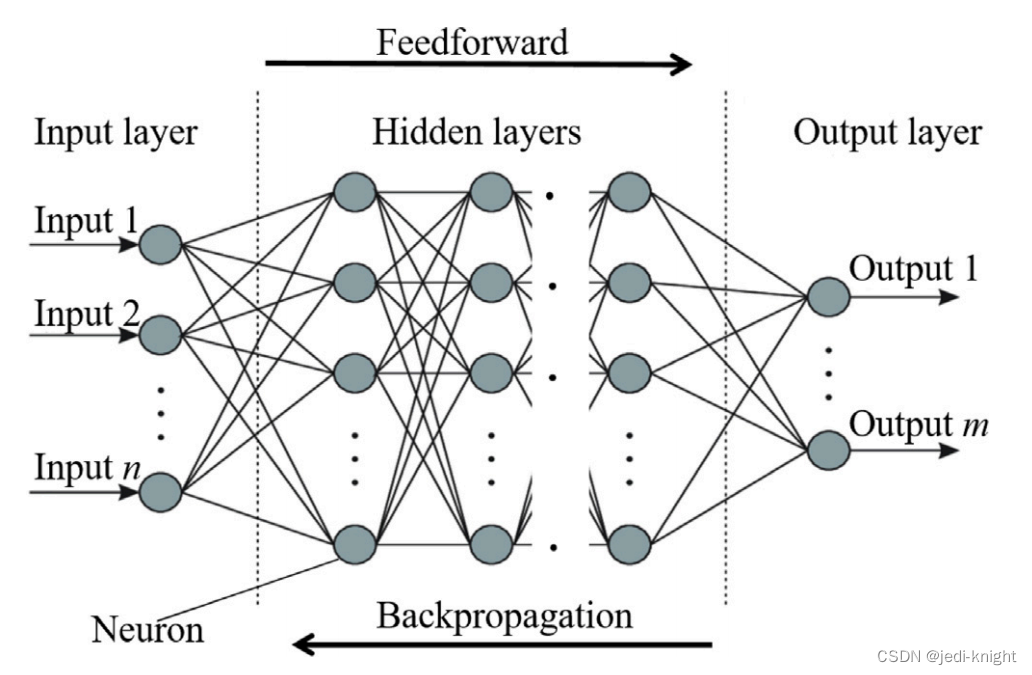
PINN的神经网络通常都十分简单，输入空间坐标，经过隐藏层后，输出位移场。对于二维问题则输出两个量，对于三维问题则输出三个量。之所以要使用神经网络来表示解，是因为：
（1）神经网络是可微分的，使用自动求导机制可以精确地获得输出对输入的偏导数
（2）神经网络可以逼近任意复杂的连续函数。
位移边界条件的定义方式可参见²
$$\hat{\mathbf{u}}(\mathbf{X},\mathbf{\varphi })=\mathbf{A}(\mathbf{X})+\mathbf{B}(\mathbf{X})\circ \hat{\mathbf{y}}(\mathbf{X},\mathbf{\varphi })$$$B(X)$为距离函数，当$X$落在位移边界条件上时，$B$为0。$A(X)$表示边界上的位移分布

应力边界条件以外力虚功的形式引入损失函数

损失函数为总势能，如下
$$\mathcal{L}={\int }_{\Omega }\hat{\psi }(\mathbf{X},\mathbf{\varphi })d\Omega -{\int }_{\Gamma }{\hat{\mathbf{u}}}^T(\mathbf{X},\mathbf{\varphi })\overline{\mathbf{t}}d\Gamma$$第一项为整个体系的应变能，第二项为外力势能 (定义为外力在结构从变形状态恢复为原始状态时所做的功，数值上等于结构以恒定力从未变形状态加载到变形状态时所做功的负值，所以有一个负号)。特别地，如果只有位移边界条件而不存在应力边界条件，那么边界上的功为0.

损失函数达到最小即系统处于最小势能状态。此时，任意虚位移下，总势能都不变，内力虚功与外力虚功之和为0，系统处于平衡状态。

对于不同的材料（线弹性材料、超弹性材料、黏弹性材料），应变能密度$\hat{\psi }$的表达式都是不同的，列于下方，具体含义见³。

线弹性材料

$$\psi =\frac{1}{2}{\epsilon }_{ij}{\sigma }_{ij}$$
应力由应变得到
$$\mathbf{\sigma }=\lambda \mathrm{trace}(\epsilon )\mathbf{I}+2\mu \mathbf{\epsilon }$$应变由位移得到
$$\mathbf{\epsilon }=\frac{1}{2}\left(\nabla \mathbf{u}+\nabla {\mathbf{u}}^T\right)$$

超弹性材料

$$\psi =\sum _{r=1}^M\frac{3^{1-{\alpha }_r}}{2{\alpha }_r}{\mu }_r\left(I_1^{{\alpha }_r}-3^{{\alpha }_r}\right)-\sum _{r=1}^M{\mu }_r\ln J+\frac{\lambda }{2}(J-1{)}^2$$
第一不变量$I_1$、行列式$J$等由变形梯度张量$\mathbf{F}$确定

黏弹性材料

$$\psi =\left[\frac{1}{2}{\epsilon }_{ij}{L}_{ijkl}^0{\epsilon }_{kl}+\frac{1}{2}\left({\epsilon }_{ij}-{\epsilon }_{ij}^v\right)L_{ijkl}^1\left({\epsilon }_{kl}-{\epsilon }_{kl}^v\right)\right]+\left[\Delta t\frac{1}{2}{\dot{\epsilon }}_{ij}^v{M}_{ijkl}^{}{\dot{\epsilon }}_{kl}^v\right]$$
注意，第二项中含有时间

---

1. E W., Yu B. The Deep Ritz Method: A Deep Learning-Based Numerical Algorithm for Solving Variational Problems[J]. Communications in Mathematics and Statistics, 2018, 6(1): 1-12 ↩︎

2. Rao C., Sun H., Liu Y. Physics-Informed Deep Learning for Computational Elastodynamics without Labeled Data[J]. Journal of Engineering Mechanics, 2021, 147(8): 4021043 ↩︎

3. Abueidda D.W., Koric S., Guleryuz E., et al. Enhanced physics-informed neural networks for hyperelasticity[J]. International Journal for Numerical Methods in Engineering, 2023, 124(7): 1585-1601 ↩︎