数据挖掘day02-微积分的本质04~06

04、直观理解链式法则和乘法法则

Q1、复合函数如何求导？

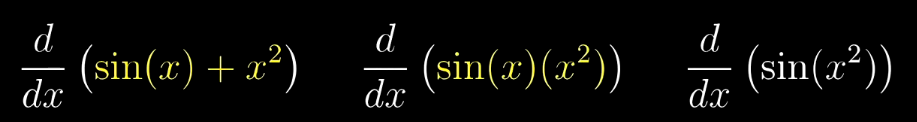
1.1、对于加法法则：两个函数的和的导数，就是他们的导数和

用下图形解析$\frac{d}{dx}(sin(x)+x^2)$:

从几何意义$d(sin(x)+x^2)$指函数$sin(x)+x^2$在$y$轴的增量，等于$dsin(x)+d{x}^2$

$\frac{d}{dx}(sin(x)+x^2)=\frac{dsin(x)+d{x}^2}{dx}=\frac{dsin(x)}{dx}+\frac{d{x}^2}{dx}$

1.2、对于乘法法则：左乘右导，右乘左导

如下图，函数$f(x)=g(x)h(x)$的增量，即绿色部分面积（忽略红色部分，极小值），同时求导，则得出结果：

1.3、链式法则：

举例：$g(x)=sin(x^2)$如何求导？

增加一个中间函数 $h(x)$ ，则$g(x)=sin(x)$，$h(x)=x^2$

$x$的变换导致$h(x)=x^2$变化，导致$g(x)=sin(x)$的变化

函数$g(x)=sin(x)$的变化量$d(sin(h))=cos(h)dh$（提示：$df$是函数变化量，$\frac{df}{dx}$才是求导）

其导数为$\frac{d}{dx}(sin(h))=cos(h)\frac{dh}{dx}$，这就是链式法则（下图）：

代入$h(x)=x^2$ 得：$\frac{d}{dx}(sin(h))=cos(x^2)2x$

05、指数函数求导？

首先考虑$M(t)=2^t$:

$\frac{dM}{dt}(t)=\frac{2^{t+dt}-2^t}{dt}=2^t\left(\frac{2^{dt-1}}{dt}\right)$

同理，$\frac{d(8^t)}{dt}=8^t\left(\frac{8^{dt-1}}{dt}\right)$，其实通过代入非常小的数发现，右侧括弧内都是常数，如下图：

那么，是否存在一个数使右侧常数为1？这样该数的求导就是它本身了。假设该数是e

即：$\frac{e^{dt-1}}{dt}=1$，$\frac{d(e^t)}{dt}=e^t$

这时候定义一个函数，将所有$n^t$，可以写作$e$的函数，基于指数的特性，令$e^x=n$，$n^t=e^{xt}$

就变成一个复合函数求导，基于$e^t$的导数为其自身，这下就可以求导了：$\frac{d(n^t)}{dt}=\frac{d(e^{xt})}{dt}=x{e}^{xt}$

那么定义该函数可以定义为：$x=lo{g}_{e}n$，即对数，由于e为常数，$lo{g}_{e}n$又写做$ln(n)$

$\frac{d(n^t)}{dt}=x{e}^{xt}=ln(n)e^{ln(n)t}=ln(n)n^t$

对比最开始$M(t)=2^t$的求导结果，右侧括弧内的常数可知：$ln(n)=\frac{n^{dt-1}}{dt}$

其实，对比上面的解释，我觉得更应该是这样的：

某数学家推算到这个结果：$\frac{d{2}^t}{dt}=2^t\left(\frac{2^{dt-1}}{dt}\right)$

然后，发现当$dt$趋于零时，$\frac{2^{dt-1}}{dt}$可能是常数，令$f(2)=\frac{2^{dt-1}}{dt}$

根据复合函数求导规则，$\frac{d{2}^t}{dt}=2^{t}f(2)$,则原函数写成关于$f(2)t$的复合函数更合适，假设存在未知数$e$令：$e^{f(2)}=2$

那么就可以写成：$\frac{d{e}^{f(2)t}}{dt}=2^{t}f(2)$，完全符合链式法则,最后定义$f(x)$ 为$ln(x)$。

06、隐函数求导是怎么回事？

Q1、对$x^2+y^2=5$,求导是怎么回事？

毫无疑问，求$\frac{dy}{dx}$可以看做是求直径$d=5$的圆上的点的斜率，如下图：

如果觉得奇怪，也可以这么理解：

1个5米的梯子放在墙上，向下滑动，上端滑动速度是$\frac{dy}{dt}=1m/s$，求下端移动速度$\frac{dx}{dt}$

如下图,代入其中一点$(x=3,y=4)$得$\frac{dx}{dt}=\frac{4}{3}$

这个例子，无非就是让它动起来，有现实意义，比上一个例子好理解。

Q2、对$y=ln(x)$,求导是怎么回事？

又例如下图，当$y=ln(x)$时，$\frac{dy}{dx}=\frac{1}{x}$

其实，这一节只是说明当两个量相关时，他们是如何变化的，为后面多元微积分入门铺路。