NOMA学习笔记

叠加编码

        非正交多址接入 (NOMA) 是 5G 的候选多址接入方案。NOMA 允许多个用户使用同一频率同时发送和接收这一事实可能看起来很有趣。使 NOMA 成为可能的两个关键操作是必须在发射机侧完成的叠加编码和在接收机侧的连续干扰消除（也称为 SIC）。

        假设两个用户用户 1 和用户 2 将使用相同频率同时通信。设 x 1表示用户 1 的数据，x 2表示用户 2 的数据。为简单起见，让我们假设每个用户只有 4 位数据要发送。

设 x 1 = 1010 和 x 2 = 0110

 x 1和x 2在传输前必须经过数字调制。使用 BPSK。BPSK 将 0 映射到 -1，将 1 映射到 +1。BPSK调制后，x 1被映射到+1 -1 +1 -1，x 2被映射到-1 +1 +1 -1，如下所示。

NOMA 要求在发射端进行叠加编码x = √a 1 x 1 + √a 2 x 2
使用了固定功率分配，假设我们给用户 1 的权重为 a 1 =0.75，给用户 2 的权重为 a 2 =0.25。
这样就得到x = 0.366 -0.366 1.366 -1.366

 以下是叠加编码的相关代码：

clc; clear all; close all;

x1 = [1 0 1 0];
x2 = [0 1 1 0];

xmod1 = 2*x1-1;
xmod2 = 2*x2-1;

a1 = 0.75; a2 = 0.25;
x = sqrt(a1)*xmod1 + sqrt(a2)*xmod2;

ay = -2:0.2:2;
ax = ones(1,length(ay));

figure;
subplot(2,1,1)
stairs([x1,x1(end)],'linewidth',2);
ylim([-2 2])
grid on; hold on;
title('Data of user 1 (x_1)')
for u = 1:3
   plot(ax*(u+1),ay,':k','linewidth',2);  
end
subplot(2,1,2)
stairs([x2,x2(end)],'m','linewidth',2);
ylim([-2 2])
grid on; hold on;
for u = 1:3
   plot(ax*(u+1),ay,':k','linewidth',2);  
end
title('Data of user 2 (x_2)')


figure;
subplot(2,1,1)
stairs([xmod1,xmod1(end)],'linewidth',2);
ylim([-2 2])
grid on; hold on;
title('Data of user 1 (x_1)')
for u = 1:3
   plot(ax*(u+1),ay,':k','linewidth',2);  
end
subplot(2,1,2)
stairs([xmod2,xmod2(end)],'m','linewidth',2);
ylim([-2 2])
grid on; hold on;
for u = 1:3
   plot(ax*(u+1),ay,':k','linewidth',2);  
end
title('Data of user 2 (x_2)');

t1 = sqrt(a1)*xmod1;
t2 = sqrt(a2)*xmod2;
figure;
subplot(2,1,1)
stairs([t1,t1(end)],'linewidth',2);
ylim([-2 2])
grid on; hold on;
title('Scaled data of user 1 ($$\sqrt{a_1}x_1$$)','Interpreter','latex','FontSize',13)
for u = 1:3
   plot(ax*(u+1),ay,':k','linewidth',2);  
end
subplot(2,1,2)
stairs([t2,t2(end)],'m','linewidth',2);
ylim([-2 2])
title('Scaled data of user 2 ($$\sqrt{a_2}x_2$$)','Interpreter','latex','FontSize',13)
grid on; hold on;

for u = 1:3
   plot(ax*(u+1),ay,':k','linewidth',2);  
end

figure;
stairs([x,x(end)],'r','linewidth',2);
grid on; hold on;
for u = 1:3
   plot(ax*(u+1),ay,':k','linewidth',2);  
end
title('Superposition coded signal')

连续干扰消除（SIC）

SIC算法：

• 直接对x进行解码，得到高功率的信号。例如，如果 x1被赋予更多权重（即 a 1 > a 2），则 x 的直接解码给出 x1。
• 将第1步解码后的信号乘以其对应的权重，并从x中减去。例如，如果上一步解码了x 1 ，则x减去√a 1 x 1 。这会给我们 x - √a 1 x 1。
• 对第二步得到的信号进行解码，得到低功率复用后的另一个信号。例如，从上一步获得的x - √a 1 x 1的解码将产生我们的 x 2

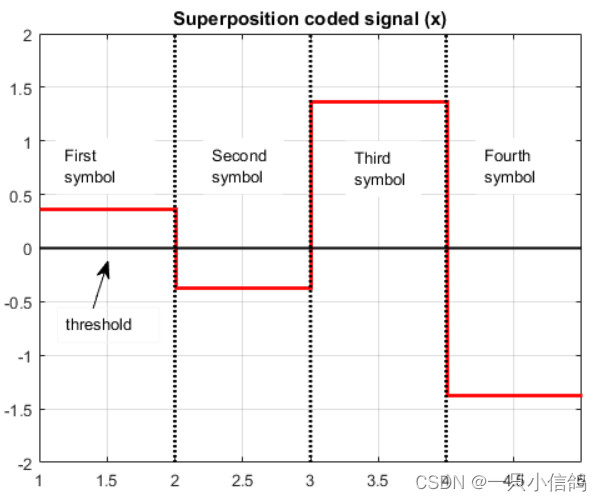
 这是 x 的图，阈值表示为黑色水平实线。观察到第一个和第三个符号位于零阈值之上。因此，我们决定第一个和第三个传输的位是 1。第二个和第四个符号位于阈值下方。因此，第二个和第四个传输位为零。因此，按顺序解码的序列为 1010。这与 x1相同！

将 x1分量乘以其相应的幂权重，然后从 x 中减去它。减法后，只需像以前一样使用 BPSK 规则解调即可，以下是完整叠加编码和SIC解码的代码。

clc; clear all; close all;

x1 = [1 0 1 0];
x2 = [0 1 1 0];

xmod1 = 2*x1-1;
xmod2 = 2*x2-1;

a1 = 0.75; a2 = 0.25;
x = sqrt(a1)*xmod1 + sqrt(a2)*xmod2;

xdec1 = ones(1,length(x1));
xdec1(x<0)=-1;

xrem = x - sqrt(a1)*xdec1;
xdec2 = zeros(1,length(x1));
xdec1(x<0)=0;
xdec2(xrem>0)=1;

%Plot figures

ay = -2:0.2:2;
ax = ones(1,length(ay));

figure;
subplot(2,1,1)
stairs([x1,x1(end)],'linewidth',2);
ylim([-2 2])
grid on; hold on;
title('Data of user 1 (x_1)')
for u = 1:3
   plot(ax*(u+1),ay,':k','linewidth',2);  
end
subplot(2,1,2)
stairs([x2,x2(end)],'m','linewidth',2);
ylim([-2 2])
grid on; hold on;
for u = 1:3
   plot(ax*(u+1),ay,':k','linewidth',2);  
end
title('Data of user 2 (x_2)')


figure;
subplot(2,1,1)
stairs([xmod1,xmod1(end)],'linewidth',2);
ylim([-2 2])
grid on; hold on;
title('Data of user 1 (x_1)')
for u = 1:3
   plot(ax*(u+1),ay,':k','linewidth',2);  
end
subplot(2,1,2)
stairs([xmod2,xmod2(end)],'m','linewidth',2);
ylim([-2 2])
grid on; hold on;
for u = 1:3
   plot(ax*(u+1),ay,':k','linewidth',2);  
end
title('Data of user 2 (x_2)');

t1 = sqrt(a1)*xmod1;
t2 = sqrt(a2)*xmod2;
figure;
subplot(2,1,1)
stairs([t1,t1(end)],'linewidth',2);
ylim([-2 2])
grid on; hold on;
title('Scaled data of user 1 ($$\sqrt{a_1}x_1$$)','Interpreter','latex','FontSize',13)
for u = 1:3
   plot(ax*(u+1),ay,':k','linewidth',2);  
end
subplot(2,1,2)
stairs([t2,t2(end)],'m','linewidth',2);
ylim([-2 2])
title('Scaled data of user 2 ($$\sqrt{a_2}x_2$$)','Interpreter','latex','FontSize',13)
grid on; hold on;

for u = 1:3
   plot(ax*(u+1),ay,':k','linewidth',2);  
end

figure;
stairs([x,x(end)],'r','linewidth',2);
grid on; hold on;
for u = 1:3
   plot(ax*(u+1),ay,':k','linewidth',2);  
end
title('Superposition coded signal')
plot(1:5,zeros(1,5),'k','linewidth',1.5)

figure;
stairs([xrem,xrem(end)],'r','linewidth',2);
grid on; hold on;
for u = 1:3
   plot(ax*(u+1),ay,':k','linewidth',2);  
end
title('Superposition coded signal')
plot(1:5,zeros(1,5),'k','linewidth',1.5)