瑞利衰落信道中非正交多址 (NOMA) BER 的仿真 - MATLAB 代码及解释

最新推荐文章于 2025-02-25 15:28:05 发布

一只小信鸽

最新推荐文章于 2025-02-25 15:28:05 发布

阅读量1.7k

点赞数 4

文章标签： matlab 开发语言

本文链接：https://blog.csdn.net/weixin_43344447/article/details/129426317

版权

该文探讨了非正交多址接入(NOMA)在基站到两个不同距离用户的下行链路传输中的应用。通过给远方用户更多的功率权重，实现了用户公平性。文中详细描述了信号生成、BPSK调制、超级编码过程以及解码策略，包括远用户和近用户的误比特率(BER)计算。通过对不同功率下的仿真，展示了容量图和理论分析的BER比较。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

考虑从基站 (BS) 到两个用户的下行链路传输，d1和d2表示它们与 BS 的距离。

BS 有两个不同的消息X1给用户 1（远用户），以及X2给用户 2（近用户）。在 NOMA 中，为了促进用户的公平性，给远方用户更多的权重，给近方用户更少的权重。那是，α1>α2个. H1和H2分别表示基站到远端用户和近端用户的信道。

BS 发送的信号为：

x =√P(√α1*X1+√α2*X2）

过信道传播后在远用户处接收

y1=h1x+w1

直接解码将X2将被视为干扰。远用户的信噪比为

可达到的数据速率是

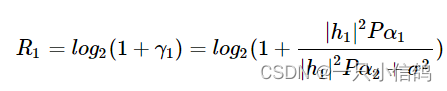
远用户接受到的是

y2=h2x+w2

用户 2在解码他自己的信号之前必须首先执行SIC，在 SIC 之前）的用户 2 处的信号干扰噪声比为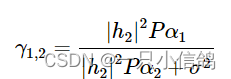

可达到的数据速率是

经过SIC后，信噪比变为：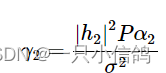

可达速率为

在不同功率下，得到容量图：

clc; clear variables; close all;

N = 10^6;

d1 = 1000; d2 = 500;    %Distances of users from base station (BS)
a1 = 0.75; a2 = 0.25;   %Power allocation factors
eta = 4;                %Path loss exponent

%Generate rayleigh fading coefficient for both users
h1 = sqrt(d1^-eta)*(randn(1,N)+1i*randn(1,N))/sqrt(2);
h2 = sqrt(d2^-eta)*(randn(1,N)+1i*randn(1,N))/sqrt(2);

g1 = (abs(h1)).^2;
g2 = (abs(h2)).^2;

Pt = 0:2:40;                %Transmit power in dBm
pt = (10^-3)*10.^(Pt/10);   %Transmit power in linear scale
BW = 10^6;                  %System bandwidth
No = -174 + 10*log10(BW);   %Noise power (dBm)
no = (10^-3)*10.^(No/10);   %Noise power (linear scale)

%Generate noise samples for both users
w1 = sqrt(no)*(randn(1,N)+1i*randn(1,N))/sqrt(2);
w2 = sqrt(no)*(randn(1,N)+1i*randn(1,N))/sqrt(2);

%Generate random binary data for two users
data1 = randi([0 1],1,N);  %Data bits of user 1
data2 = randi([0 1],1,N);  %Data bits of user 2

%Do BPSK modulation of data
x1 = 2*data1 - 1;
x2 = 2*data2 - 1;

p = length(Pt);
for u = 1:p
    %Do superposition coding
    x = sqrt(pt(u))*(sqrt(a1)*x1 + sqrt(a2)*x2);
    %Received signals
    y1 = h1.*x + w1;
    y2 = h2.*x + w2;
    
    %Equalize 
    eq1 = y1./h1;
    eq2 = y2./h2;
    
    %AT USER 1--------------------
    %Direct decoding of x1 from y1
    x1_hat = zeros(1,N);
    x1_hat(eq1>0) = 1;
    
    %Compare decoded x1_hat with data1 to estimate BER
    ber1(u) = biterr(data1,x1_hat)/N;
    
    %----------------------------------
    
    %AT USER 2-------------------------
    %Direct decoding of x1 from y2
    x12_hat = ones(1,N);
    x12_hat(eq2<0) = -1;
    
    y2_dash = eq2 - sqrt(a1*pt(u))*x12_hat;
    x2_hat = zeros(1,N);
    x2_hat(real(y2_dash)>0) = 1;
    
    ber2(u) = biterr(x2_hat, data2)/N;
    %-----------------------------------   
    
    gam_a = 2*((sqrt(a1*pt(u))-sqrt(a2*pt(u)))^2)*mean(g1)/no;
    gam_b = 2*((sqrt(a1*pt(u))+sqrt(a2*pt(u)))^2)*mean(g1)/no;
    ber_th1(u) = 0.25*(2 - sqrt(gam_a/(2+gam_a)) - sqrt(gam_b/(2+gam_b)));
    
    gam_c = 2*a2*pt(u)*mean(g2)/no;
    gam_d = 2*((sqrt(a2) + sqrt(a1))^2)*pt(u)*mean(g2)/no;
    gam_e = 2*((sqrt(a2) + 2*sqrt(a1))^2)*pt(u)*mean(g2)/no;
    gam_f = 2*((-sqrt(a2) + sqrt(a1))^2)*pt(u)*mean(g2)/no;
    gam_g = 2*((-sqrt(a2) + 2*sqrt(a1))^2)*pt(u)*mean(g2)/no;
    
    gc = (1 - sqrt(gam_c/(2+gam_c)));
    gd = (1-sqrt(gam_d/(2+gam_d)));
    ge = (1-sqrt(gam_e/(2+gam_e)));
    gf = (1-sqrt(gam_f/(2+gam_f)));
    gg = (1-sqrt(gam_g/(2+gam_g)));
    
    ber_th2(u) = 0.5*gc - 0.25*gd + 0.25*(ge+gf-gg);
    
    gamma1(u) = a1*pt(u)*mean(g1)/(a2*pt(u)*mean(g1) + no);
    gamma2(u) = a2*pt(u)*mean(g2)/no;
end

semilogy(Pt, ber1,'r', 'linewidth',1.5); hold on; grid on;
semilogy(Pt, ber2,'b', 'linewidth',1.5);
semilogy(Pt, ber_th1, '*r','linewidth',1.5);
semilogy(Pt, ber_th2, '*b','linewidth',1.5);
xlabel('Transmit power (P in dBm)');
ylabel('BER');
legend('Sim. User 1/Far user','Sim. User 2/Near user','Theo. User 1/Far user','Theo. User 2/Near user');