摘要
为了在时变通信系统中实现高效可靠的数据传输,提出了一种基于无速率码(NOMA-RC)的下行非正交多址系统。NOMA-RC系统可以根据解码结果在限定时间内连续向用户发送叠加信号。用户成功解码信号后,它将向发射机发送确认信号。然后系统可以调整要发送的消息,以提高剩余用户的解码概率。分析了具有延迟约束的NOMA-RC系统在中上衰落信道下的性能。仿真结果表明,与基于无速率码的正交多址接入系统相比,NOMA-RC系统能够减少传输时间,提高系统效率。
介绍
解决的问题
随着第五代(5G)移动通信在频谱效率和用户连接数方面的需求的快速增长,正交多址接入(OMA)系统越来越难以满足这一趋势。非正交多址接入(NOMA)技术是提高系统容量和频谱效率的有效途径,是下一代移动通信网络很有前途的多址接入方案。
采取的方案
但在时变信道条件下的无源多动系统也没有得到很好的研究。对于固定速率码的通信系统,需要频繁地估计信道状态,然后选择合适的编码速率和调制方式发送消息。不幸的是,这类系统很难在时变信道下获得高性能。无速率码在不提前知道信道状态信息(CSI)[8] -[11]的情况下,在不利条件下自动调整速率。发射机可以连续地产生许多相互依赖的编码符号。如果接收方解码失败,发送方会添加一些新的符号来共同解码。无率码大部分是在瑞利衰落信道中开发的,而现有的贡献缺乏在中上衰落信道中使用无率码。具体来说,Nakagami-m衰落信道可以根据m的大小缩小为不同的信道。例如,当m =1时,为瑞利衰落信道。当使用时,也可以将其转换为衰落参数为k的Rice衰落信道。
系统模型
用户界面与BS之间的信道增益表示为,∀1≤i≤m0,其中m0为总用户数。我们假设用户和BS之间的信道是独立的,并遵循Nakagami-m分布。因此,
的概率密度函数(PDF)和累积分布函数(CDF)表示为

其中m决定了衰落信道的类型。参数Ωi为Ui的平均接收功率

式中Pt表示BS的传输功率,K为与每个天线单元相关的常数系数和平均信道损耗,τ为路径损耗指数,d为用户到BS的距离。
来自用户的信息由无速率编码器编码,生成一些符号,然后与相应的功率因数相乘,形成要传输的复合信号。Ui接收到的信号为

式中ni为加性高斯白噪声,ai为分配的功率因数。ai要满足

其中![]() , εi为中断概率,Pσ2噪声的平均功率,且a1≥a2≥···≥ai≥···≥am0,∀0≤ai≤1。
, εi为中断概率,Pσ2噪声的平均功率,且a1≥a2≥···≥ai≥···≥am0,∀0≤ai≤1。
ai的详细推导见:
J. Cui, Z. Ding, and P. Fan, “A novel power allocation scheme under
outage constraints in NOMA systems,” IEEE Signal Process. Lett.,
vol. 23, no. 9, pp. 1226–1230, Sep. 2016.
信息传输的过程
以两个用户为例,描述了准静态衰落信道下的通信过程。整个沟通过程分为两个阶段。
- 当BS同时向两个用户发送叠加信号时,当有一个成功解码用户时,第一阶段结束。
- 在第二阶段,BS可以根据成功用户的反馈来调整剩余用户的传输功率。
由于每个阶段参与用户的数量不同,通道的状态也会发生变化。假设信道是准静态衰落信道,即CSI在同一相位保持不变,但不同相位之间的状态是相互独立的。近端用户Un解码远端用户Uf所需时间为

其中![]()
用户Un可以使用SIC算法消除Uf信号,然后解码自己的信息。Un所需的时间是
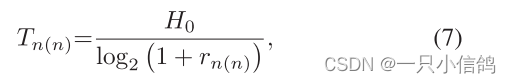
其中![]()
假设成功解码Ui记为Dn(i)。对于Un,只有Dn(f)和Dn(n)同时解码成功后,用户的ACK才发送给BS。所以Un成功解码的时间是Tn,1 =max(Tn(f) ,Tn(n))。
对于Uf,Uf将Un的信息作为干扰信号处理。故其时间为
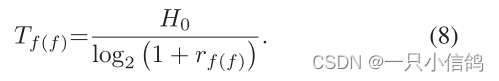
第一段解码时间为T1 = min (Tn,1,Tf(f))。然后,BS继续向剩余的用户发送相关信息,直到成功。所以两个用户需要的总时间是
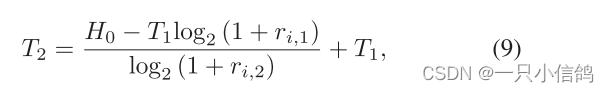
其中,ri,1为失败用户Ui (i = n, f)在第一阶段的SINR, ri,2为用户Ui在第二阶段的SINR。chua
两种传输方案
-
理想的传输方案
BS使用无速率编码器生成无限多个不同的符号。只要积累了足够的符号,用户就能够以接近1的概率完成解码。因此,在NOMA-RC系统没有传输时间限制的情况下,双方用户都成功解码。下面有两种情况需要讨论。
1) Un first, Uf second:用户Un先解码Uf,然后再解码自己的消息。对于Un,需要满足以下表达式:

其中rn,1=min (rn(f) ,rn(n))
定理1:rn,1的PDF的封闭表达式
其中a = Ptaf,b = Ptan,c = Pσ2, Ωn是Un接收到的平均功率
定理2:在第一阶段,Uf单位时间的信息积累为y=log2 (1 + rf,1)。y的PDF为
其中Ωf为Uf的平均接收功率。
定理3:在第二阶段,单位时间Uf所积累的信息为u =log2 (1+ rf,2)u的PDF的封闭表达式
定理4:Uf是第一个成功的,第一阶段的时间由Uf决定,
。给出了t1的PDF的封闭表达式
-
延迟约束的传输方案
在实际系统中总是存在最长的容忍时间t。这意味着,对于失败的帧消息,BS不会一直发送符号。如果在t内无法解码信息,发送器将丢弃该信息或清除之前的符号,并重新添加一些新的符号。我们将失败消息定义为错误帧。因此,两个用户在有限的传输时间内有四种情况,下面讨论。
1)情形1:Un成功,Uf失败
在t1中Un解码成功而Uf解码失败的概率为
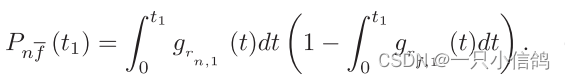
Uf在t2和平均时间下解码的概率为
2)情形2:Uf成功,Un失败
Uf解码成功而Un解码失败的概率为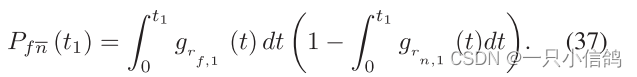
Un在t2中解码的概率为
3)情况3:Un和Uf同时成功
情况3的概率和平均时间均为0。
4)情形4:Un和Uf都失败
可以得到情形4发生的概率和两个用户的平均时间为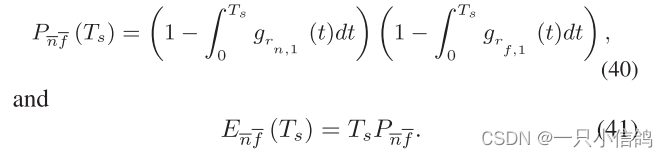
具有延迟约束的系统处理这两个用户的平均时间为

仿真结果
通过nakagami信道的仿真实验,给出了NOMA-RC系统的性能。本节分析和讨论系统的平均传输时间和帧误码率(FER)性能。假设有两个用户Un和Uf,他们与BS的距离分别设为d1 = 1000m和d2 = 500m。其他模拟参数为:K=−38.757,τ =3.71,d0 =1, Pσ2 =−108dBm, af =0.2, an =0.8。
(K为与每个天线单元相关的常数系数和平均信道损耗,τ为路径损耗指数,Pσ2噪声的平均功率)
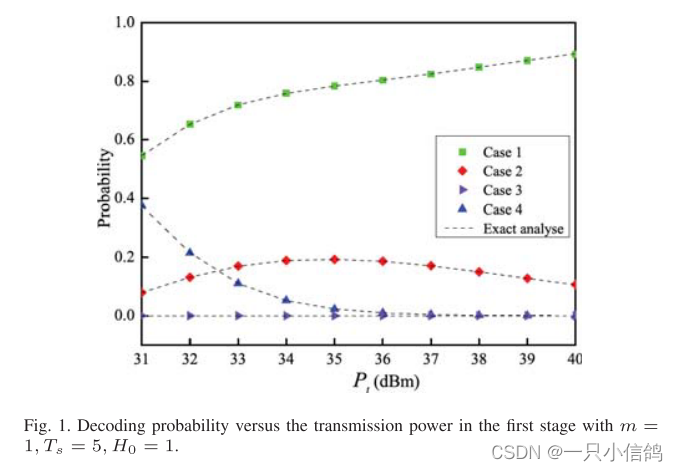
从图1中可以看出,Case 1随着Pt的增加而增加,而Case 4则继续减少。Un用户在第一阶段可以快速成功,Uf用户成功的概率相对较低。

图2显示了NOMA-RC和OMA使用无速率码系统在nakagami信道上处理两个用户所需的传输时间。当Pt值较小时,每个用户的解码失败概率相对较高。由于最大延迟限制,系统被迫终止消息的传输。因此,平均传输时间更长。随着Pt的增加,用户单位时间内积累的信息越多,完成解码所需的时间越少。此外,随着m的增加,曲线下降得更快。与OMA系统相比,NOMA-RC系统可以在时变信道中同时传输多个用户的数据,因此相同m所需的传输时间更少。

用户可以通过不断积累相互信息来获得成功。也就是说,即使在低信噪比的情况下,也可以通过延长传输时间来完成解码。由于最大传输时间的限制,NOMA-RC系统必须在t时间内做出响应。图3和图4分别为用户通过Nakagami-m信道和不同t时的FER性能。随着t的增加,用户积累的互信息越多,他们获得成功的概率就越大。例如,当传输功率为38dbm时,当Ts=3和Ts=8时,系统的FER分别为8.39×10−4和6.2 ×10−3。因此,改善信道条件、延长传输时间是提高FER性能的有效途径。特别是对于存储能量有限的设备,我们可以延长时间,以确保通信的可靠性。对于一些具有低延迟要求的应用,系统可以通过增加传输功率来减少时间。
结论
提出了一种基于无速率码的中上衰落信道NOMA传输方案。由无速率编码器产生的每个用户的符号乘以BS中的功率因数。这些信号叠加在一起形成若干个复合信号,同时传送给每个用户。NOMA-RC系统能够利用无速率编码器为每个用户生成许多不同的符号,提高了抗噪声能力。此外,每个用户可以通过累积之前接收到的符号来共同解码,提高频谱效率。实验表明,NOMA-RC系统可以减少传输时间,有助于提高FER性能。此外,还可以根据不同的应用场景,调整最大传输时间或传输功率,以满足不同的需求。








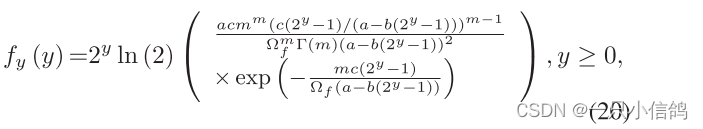
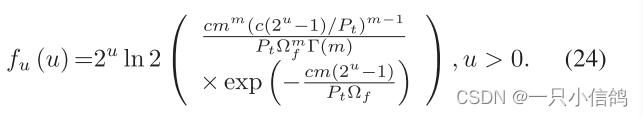
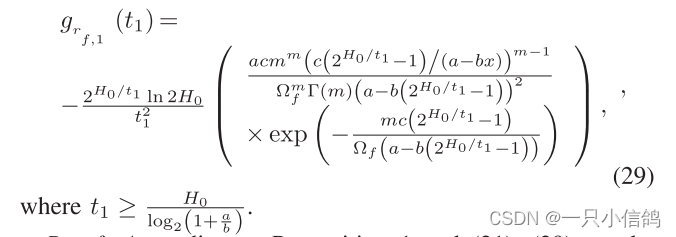
















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








