九 . (未做：87，282，） LeetCode标签刷题—— DFS+递归+回溯+BFS 算法部分

回溯算法的基本思想是：从一条路往前走，能进则进，不能进则退回来，换一条路再试。自己画出来递归搜索树。

17. 电话号码的字母组合

给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。答案可以按 任意顺序 返回。

给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。

示例 1：

输入：digits = "23"
输出：["ad","ae","af","bd","be","bf","cd","ce","cf"]
示例 2：

输入：digits = ""
输出：[]

示例 3：

输入：digits = "2"
输出：["a","b","c"]

提示：

0 <= digits.length <= 4
digits[i] 是范围 ['2', '9'] 的一个数字。

算法分析：
递归：

最坏情况下时间复杂度：
时间复杂度 O(4ⁿ X n)
一个数字最多有4种情况，假设有n个数字，因此4ⁿ种情况是一个上限，因此时间复杂度是 O(4ⁿ X n)

算法分析
枚举+dfs

1、先把数字和字符对应在一个哈希表或者数组中
2、dfs(String digits,int u,String path)：path表示当前已经有什么元素，u表示枚举到digitis的第u个字母，从哈希表或者数组中找到第u个字母对应的几个字符，分别进行枚举拼接到path后面

代码：

class Solution {
public:
    vector<string> res;    //定义全局答案数组
    string strs[10] =	{"","","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"};    
    //为了方便的表示和求出一个数字对应的字母，我们可以开一个数组来表示。其中0和1对应的为空，所以写空字符串。
    vector<string> letterCombinations(string digits) {
    	//特判一定要写！！！//空串特判
        if(digits.size()==0)return res; //字符串为空，返回空
        dfs(digits,0,"");   //开始递归，递归起始下标是0，最开始路径为空
        return res; //递归结束将答案返回
    }
    void dfs(string digits,int u,string path){  //编写dfs函数，传入的参数包括要求的字符串，枚举到第几位了，以及记录的当前路径
        if(u==digits.size())res.push_back(path);    //如果已经枚举到最后一位，说明当前方案就是一个答案，我们就将当前方案加到答案数组中。
        else{   //否则的话，我们就遍历一下当前下表能取那些值
        	//遍历所给的字符串中的每个字符 递归到下一层
            for(auto c:strs[digits[u]-'0']){    //枚举下表u对应的字母c,注意这里是strs[digits[u]-'0'];
            	// path 拼接 字符
                dfs(digits,u+1,path+c);    //将c加到答案里去，继续对下一个下标（u+1）进行递归
            }
        }
    }
};

java代码：

class Solution {
    List<String> res=new ArrayList<>();
    String[] strs={"","","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"};
    public List<String> letterCombinations(String digits) {
        if(digits.length()==0) return res;
        dfs(digits,0,"");
        return res;
    }
    //u:digits的当前下标
    void dfs(String digits,int u,String path){
        if(u==digits.length()) res.add(path);
        else{
        //当前数 字符对应的字符串
            String str = strs[digits.charAt(u) - '0'];
            for(int i=0;i<str.length();i++){
                char c=str.charAt(i);
                dfs(digits,u+1,path+c);
            }
        }
    }
}

2021年8月31日17:59:10：


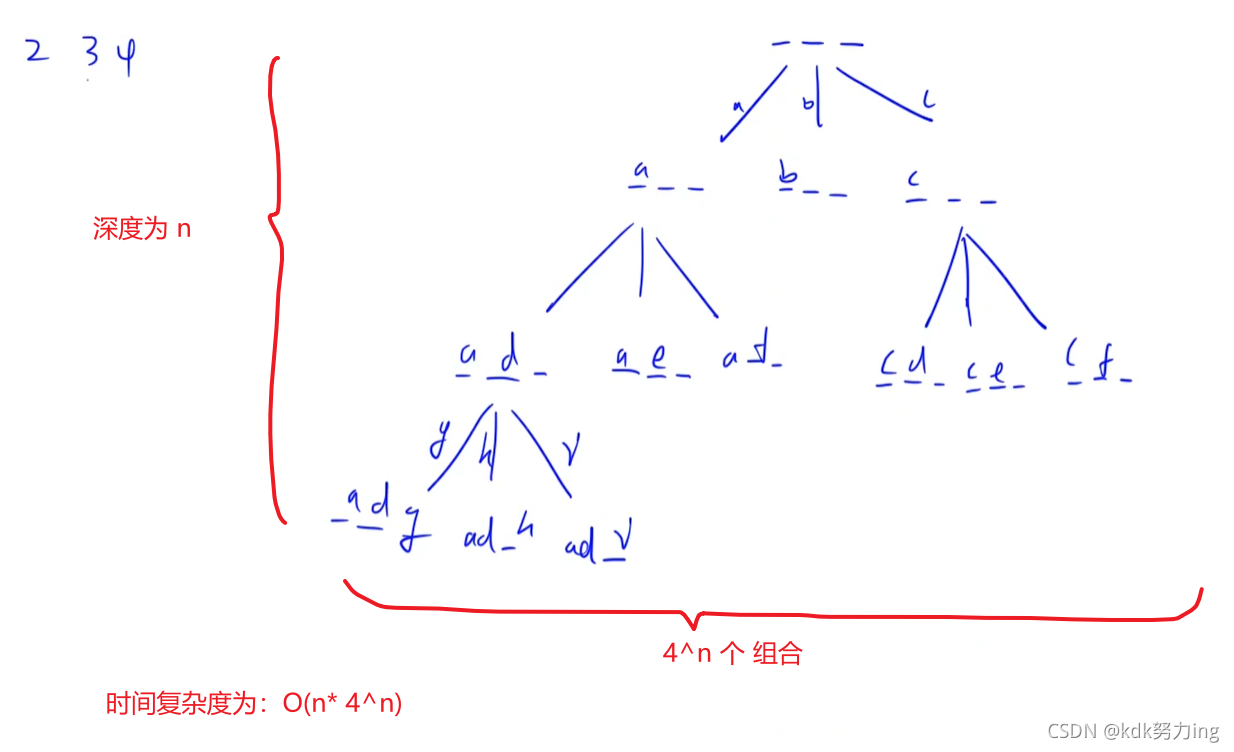
时间复杂度：n = digits.size()，把回溯画出来 最下面 一层有 4^ n 个组合，回溯树深度 为n，所以是 O(4ⁿ * n)

//dfs爆搜即可，是按照题目给定的顺序的字符进行枚举爆搜，时间：最坏情况中，每个数字有四种选择，所以最坏是4^n,add的时间是0(n),所以是O(n*4^n)
class Solution {
    List<String> res=new ArrayList<>(); //这个是最终的答案，我们定义为全局的，因为dfs函数也需要res
    String[] nums={"","","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"};  //定义键盘数字与字符的映射，因为0和1上没有字符，所以定义为空
    public List<String> letterCombinations(String digits) {
        if(digits.length()==0) return res;  //如果字符串是空，我们直接返回空字符串
        dfs(digits,0,""); //否则字符串不空，我们就从下标0开始填写，当前路径是""
        return res; //最后递归结束之后将答案返回
    }
    public void dfs(String digits,int u,String path){ //定义dfs函数，注意要将字符串digits传进去，u是当前填写到了字符串的第几位，path是填写好的当前路径
    //注意每次path都是新的，所以不需要回溯操作
        if(u==digits.length()){ //填好了路径，我们就把path加到res中
            res.add(path); //把path加到答案中,注意不是二维数组列表，所以不是new ArrayList<>(path),
            return;
        }
        else{ //否则我们就要继续往path中填写字符，即遍历一下当前位置上可以填写哪些字符
            String str=nums[digits.charAt(u)-'0'];  //取到当前字符串数组中的对应的字符，注意这里的取的方式
            for(char c:str.toCharArray()){ //否则就要枚举当前数字对应的字符型上的字符填写到当前路径上即：path+c
                dfs(digits,u+1,path+c); //继续往下一位递归，即u+1,并且path上要加上c
            }
        }
    }
}

解法二；定义path为全局的，这样我们就需要回溯了
// 回溯过程清晰展现出来

class Solution {
public:
    string map[10] = { // 可以 加 const
            "", "", "abc", "def",
            "ghi", "jkl", "mno",
            "pqrs", "tuv", "wxyz",
        }; // 要有;
    vector<string> ans;
    string path; // path做全局变量

    vector<string> letterCombinations(string digits) {
        if (digits.empty()) return ans; // 特判 字符串为空
        dfs(digits, 0);
        return ans;
    }

    void dfs(string& digits, int idx) {
        if (path.size() == digits.size()){ // idx代替path.size()也可
            ans.push_back(path);
            return;
        }
        for (auto c : map[digits[idx] - '0']){ // 横向遍历
            path.push_back(c); // 有 str+=字符, 无str-=字符 用法
            dfs(digits, idx + 1);
            path.pop_back(); // 回溯
        }
    }
};

22. 括号生成

数字 n 代表生成括号的对数，请你设计一个函数，用于能够生成所有可能的并且 有效的 括号组合。

示例 1：

输入：n = 3
输出：["((()))","(()())","(())()","()(())","()()()"]

示例 2：

输入：n = 1
输出：["()"]

提示：

1 <= n <= 8

上面的结论要保证括号相同，如都是小括号。

算法分析：
1、dfs(int n,int l,int r,String s)：n表示最多有n个左括号和右括号，l表示左括号的个数，r表示右括号的个数，s表示当前的序列
2、若l < n，左括号的个数小于n，则可以在当前序列后面拼接左括号
3、若r < l，右括号的个数小于左括号的个数，则可以在当前序列后面拼接右括号

时间复杂度 O(C_2nⁿ)
直接生成合法的序列一定满足右括号的个数总是小于等于左括号的个数，是一个典型的卡特兰数问题，卡特兰数的时间复杂度是O(C_2nⁿ)/(n+1), 后面我们还要把每个方案完整复制或者说插入到一个数组中，所以要再乘以一个2n所以总的时间复杂度是：O(C_2nⁿ)

(直接生成合法的括号序列) O(Cn2n)

使用递归。

• 1.每次可以放置左括号的条件是当前左括号的数目不超过 n。
• 2.每次可以放置右括号的条件是当前右括号的数目不超过左括号的数目。

时间复杂度
时间复杂度就是答案的个数，乘上保存答案的 O(n)计算量，该问题是经典的卡特兰数。 总时间复杂度为: O(n/n+1*C2nn)=O(C2nn)。

代码：

class Solution {
public:
    vector<string> res;   //定义答案数组
    vector<string> generateParenthesis(int n) {
        dfs(n,0,0,"");     //最开始lc和rc的数量均是0个，初始括号序列为空,因为n是局部变量，所以这里我们传入的参数要有n。
        return res;    //递归结束返回答案。  
    }
    void dfs(int n,int lc,int rc,string seq){   //编写递归函数，n是括号的对数，lc是此时左括号的数量，rc是此时右括号的数量，seq是当前的括号序列，注意返回值为空void
        //先写递归结束条件
        if(lc==n&&rc==n) res.push_back(seq);    //当左括号和右括号的数量都用光了，就说明找到了一个合法的括号序列，，就将其加到答案数组中。
        else{   //否则就说明此时递归正在进行中，
            if(lc<n)dfs(n,lc+1,rc,seq+'(');    //还可以加左括号，就递归加左括号
            if(rc<n&&rc<lc) dfs(n,lc,rc+1,seq+')') ;    //还可以加右括号，就加右括号，注意这里不能<=,如果是=，再加右括号)就会使得右括号数量大于左括号数量，不符合合法括号序列的两个条件了。
        }
    }
};

问题1：
y总你好 之前记得您说递归都要恢复现场 请问这题恢复现场的操作不用做吗？

1.因为这里传的string是直接传到 method的parameter里生成新的string。 没有更改现场的seq 值， 所以不用恢复。

2. 对滴，只要当前分支不会影响兄弟分支，就不需要恢复现场。**

问题2这里是怎么实现回溯的啊

这道题不需要回溯，回溯的一般情况是在当前层做了选择，将选择记录在路径中，然后需要做其他选择的时候，那就必须把当前层的状态清空。而这道题写法上有点不一样，每次传参数的时候直接把路径传下去了，我们没有用一个变量来保存路径。这位同学好像是用的回溯写法
https://www.acwing.com/solution/content/14263/

java代码：
注意：从一行代码复制到下一行的时候一定要注意把要改变的都改变了。

class Solution {
    List<String> res=new ArrayList<>();
    public List<String> generateParenthesis(int n) {
        dfs(n,0,0,"");
        return res;
    }
    public void dfs(int n,int lc,int rc,String seq){
        if(lc==n&&rc==n){
            res.add(seq);
            return ;
        }
        if(lc<n)dfs(n,lc+1,rc,seq+"(");
        if(rc<n&&rc<lc)dfs(n,lc,rc+1,seq+")");
    }
}

36. 有效的数独（st数组注意不是整个初始化为false,而是每一行都要初始化为false)

判断一个 9x9 的数独是否有效。只需要根据以下规则，验证已经填入的数字是否有效即可。

1. 数字 1-9 在每一行只能出现一次。
2. 数字 1-9 在每一列只能出现一次。
3. 数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。

上图是一个部分填充的有效的数独。

数独部分空格内已填入了数字，空白格用 ‘.’ 表示。

示例 1:

输入:
[
  ["5","3",".",".","7",".",".",".","."],
  ["6",".",".","1","9","5",".",".","."],
  [".","9","8",".",".",".",".","6","."],
  ["8",".",".",".","6",".",".",".","3"],
  ["4",".",".","8",".","3",".",".","1"],
  ["7",".",".",".","2",".",".",".","6"],
  [".","6",".",".",".",".","2","8","."],
  [".",".",".","4","1","9",".",".","5"],
  [".",".",".",".","8",".",".","7","9"]
]
输出: true

示例 2:

输入:
[
  ["8","3",".",".","7",".",".",".","."],
  ["6",".",".","1","9","5",".",".","."],
  [".","9","8",".",".",".",".","6","."],
  ["8",".",".",".","6",".",".",".","3"],
  ["4",".",".","8",".","3",".",".","1"],
  ["7",".",".",".","2",".",".",".","6"],
  [".","6",".",".",".",".","2","8","."],
  [".",".",".","4","1","9",".",".","5"],
  [".",".",".",".","8",".",".","7","9"]
]
输出: false
解释: 除了第一行的第一个数字从 5 改为 8 以外，空格内其他数字均与 示例1 相同。
     但由于位于左上角的 3x3 宫内有两个 8 存在, 因此这个数独是无效的。

说明:

一个有效的数独（部分已被填充）不一定是可解的。
只需要根据以上规则，验证已经填入的数字是否有效即可。
给定数独序列只包含数字 1-9 和字符 '.' 。
给定数独永远是 9x9 形式的。

算法分析：
这个题目并不要求是可解的，只需要判断已经填的是否有重复的数字即可。

class Solution {    //这个题目不用管九宫格是否有解，只要验证已经填入的数字是否有效即可。
public:     //c++中的二维数组：vector<vector<char>>& board
    bool isValidSudoku(vector<vector<char>>& board) {   
        bool st[9]; //bool数组st用于记录数字1-9（共9个数）是否出现过（一共是st[0],st[1],......st[8]共9个元素）

        //判断行是否有重复数字
        for(int i=0;i<9;i++){   //枚举每一行，看每一行上的元素是否重复
            memset(st,0,sizeof st);   //先将每一行st数组全部置为false，代表数组中元素均没有出现过，在C++中0和false等价，1和true等价。
            //注意这里st数组被我们重复使用了，所以我们在判断这一行元素之前需要先把这一行的st数组初始化为false。
            for(int j=0;j<9;j++){   //枚举每一行中的每一列上的元素board[i][j];或者说每一行的所有元素
                if(board[i][j]!='.'){   //如果当前位置上的元素非空，为空的话就不用判断了。
                    int t=board[i][j]-'1';  //把当前位置上的元素变为数字t，且为了和st[]数组保持一致，我们这里减去的是'1'，不是'0';
                    if(st[t]) return false; //如果数字t对应的st[t]]数组值不为false，即已经出现过，则直接返回false，即结束判断，此九宫格一定不合法。
                    else st[t]=true;    //如果st[t]数组值为false，即之前已经出现过，则还是合法九宫格，但我们需要令st[t]=true,即代表数字t对应的九宫格在此之后已经出现。
                }
            }
        }

        //判断列是否有重复数字
        for(int i=0;i<9;i++){   //枚举每一列，看每一列上的元素是否重复
            memset(st,0,sizeof st);   //先将st数组全部置为false，代表数组中元素均没有出现过，在C++中0和false等价，1和true等价。
            for(int j=0;j<9;j++){   //枚举每一列中的每一行上的元素board[i][j];
                if(board[j][i]!='.'){   //如果当前位置上的元素非空。注意这里是j下标在前，i下标在后，因为判断的时候，列不变，变的是行，所以变的j作为行放在前面
                    int t=board[j][i]-'1';  //把当前位置上的元素变为数字t，且为了和st[]数组保持一致，我们这里减去的是'1'，不是'0';
                    if(st[t]) return false; //如果数字t对应的st[t]]数组值不为false，即已经出现过，则直接返回false，即结束判断，此九宫格一定不合法。
                    else st[t]=true;    //如果st[t]数组值为false，即之前已经出现过，则还是合法九宫格，但我们需要令st[t]=true,即代表数字t对应的九宫格在此之后已经出现。
                }
            }
        }

        //判断每一个3X3小方格中是否有重复数字
         //(i,j)枚举每个九宫格的左上角起始坐标
         //(x,y)枚举每个九宫格内的元素
        for(int i=0;i<9;i+=3){  //每一个3X3小方格的起始行，可以取得到的值为0,3,6，主要目的是作为行偏移量使用，所以每次加3(3个3个的跳)。
            for(int j=0;j<9;j+=3){  //每一个3X3小方格的起始列，可以取得到的值为0,3,6，目的是作为列偏移量使用，所以每次加3(3个3个的跳)。
            	//将这个3X3小方格中每个数均初始化为没有出现过，即st数组初始化为false，所以我们需要在这里对3X3小方格进行初始化
                memset(st,0,sizeof st); //别忘了初始化st[]数组全为false；
                //在枚举小方格(3X3)中的所有元素，
                for(int x=0;x<3;x++){   //再枚举每一个小方格中的每一行
                    for(int y=0;y<3;y++){   //枚举每一个小方格的每一列  
                        if(board[i+x][j+y]!='.'){   //再判断小方格中的元素的时候，注意要加上偏移量，即i+x,j+y
                           int t=board[i+x][j+y]-'1';   //1~9映射到数组0~8，因为数组下标是从0开始的
                           if(st[t]==true) return false;  //如果数字重复，直接返回false即可，说明9X9大方格中有重复的数字
                           else st[t]=true; //如果st[t]为false，不能直接返回true,因为我们还没有全部判断完毕，只需要把st[t]改为true即可。
                        }
                    }
                }
            }
        }
        return true;    //最后，上面行，列，3X3小方格均没有返回false，说明这是一个有效的数独，返回true。
    }
};

2021年8月24日21:21:20：

//这个题目不用管这个数独有没有解，你就管它已经填好的是否有效合法即可，不要做无用功，模拟题，开一个布尔数组，
//分行，列，和9个3X3小方格三个部分，依次判断，只要有非法数字出现即是无效的数独，注意题目中的空白格已经用.表示了
class Solution {
    public boolean isValidSudoku(char[][] board) {
        boolean[] st=new boolean[9];  //st数组，重用st数组分别记录行，列，3X3小方格中是否有重复元素，
        //注意这里也可以开二维数组，

        //1.先判断行
        for(int i=0;i<9;i++){ //判断每一行
            Arrays.fill(st,false);   //标记每一行中的每一个数都没有重复出现过
            for(int j=0;j<9;j++){ //判断行中的每一列
                if(board[i][j]!='.'){ //如果当前元素不是'.',即已经填过数了，我们就把这个数标记为已经出现过，即标记为true
                    int t=board[i][j]-'1';  //注意我们现在要将board[i][j]这个数标记为已出现过，而数是从1开始的，数组下标是从0开始的，所以我们要减'1'
                    if(st[t]==true) return false; //先判断一下这个数在当前行中是否出现过，如果出现过就直接返回false即可
                    st[t]=true; //否则就没有重复出现过，我们就将这个数标记为true,表示已经出现一次
                }
            }
        }

        //2.如果上面没有返回false,我们就需要接着判断列，和上面判断行差不多只需要简单改一下即可,注意数组的行在前，列在后
        for(int i=0;i<9;i++){   //枚举每一列
            Arrays.fill(st,false);  //我们重用了st数组，所以我们需要重新将st数组赋值为false
            for(int j=0;j<9;j++){ //枚举每一行
                if(board[j][i]!='.'){  //注意注意注意j是行，i是列，所以这里是board[j][i]
                    int t=board[j][i]-'1';
                    if(st[t]==true) return false;
                    st[t]=true;
                }
            }
        }

        //3.如果上面没有返回false,我们就需要再判断9个3X3方格
        for(int i=0;i<9;i+=3){  //从左上角的第一个3X3方格开始，每次一个小方格行数加3，所以是i+=3，i的取值有0,3,6
            for(int j=0;j<9;j+=3){ //列也是每次跳三格，枚举顺序即是从左到右，再从上到下，j的取值有0,3,6
                Arrays.fill(st,false); //每次枚举时都要将3X3方格置为false
                //再枚举每一个3X3方格中的9个小方格
                for(int x=0;x<3;x++){   //定义x,y再分别枚举3X3方格中的9个数
                    for(int y=0;y<3;y++){
                        if(board[x+i][y+j]!='.'){  //注意x,y要加上偏移量i,j，
                            int t=board[x+i][y+j]-'1';
                            if(st[t]==true) return false;
                            st[t]=true;
                        }
                    }
                }
            }
        }
        return true;  //最后上面的行，列，3X3小方格均没有返回false，就说明这是一个有效的数独，我们返回true
    }
}

37. 解数独

编写一个程序，通过填充空格来解决数独问题。

一个数独的解法需遵循如下规则：

• 数字 1-9 在每一行只能出现一次。
• 数字 1-9 在每一列只能出现一次。
• 数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。

空白格用 '.' 表示。

一个数独。

答案被标成红色。

提示：

• 给定的数独序列只包含数字 1-9 和字符 '.' 。
• 你可以假设给定的数独只有唯一解。
• 给定数独永远是 9x9 形式的。

算法分析：
(递归回溯)

1. 首先按照 Valid Sudoku 的方法，预处理出 col、row 和 ceil 数组。
2. 从 (0,0) 位置开始尝试并递归。遇到 . 时，枚举可以填充的数字，然后判重并加入 col、row 和 ceil 数组中。
3. 如果成功到达结尾，则返回 true，告知递归可以终止。
   4.

代码：

class Solution {
public:
	//开三个数组用来记忆已经填入九宫格里的数, 每一行9个数, 每一列9个数, 每个小九宫格9个数
    bool row[9][9]; //row[x][u]表示第x(0~8)行是否已经填过数字u(0-8)，
    //注意这里是数字0-8,因为数组的特性下标是从0开始的，所以我们这里为了和数组下标保持相同，我们让数字为0-8,但是下面在填写的时候要填写1-9。
    bool col[9][9]; //col[y][u]表示第x(0~8)行是否已经填过数字u(0-8)
    bool ceil[3][3][9]; //ceil[x / 3][y / 3][u]表示第[x/3,y/3]个box是否已经填过数字u（0-8）
    //如何将i,j映射到3 X 3的小矩阵中
    // 3 x 3的矩阵可表示为:
    // 00 01 02
    // 10 11 12
    // 20 21 22 
    // 先看行i: 0-2 -> 0, 3-5 -> 1, 6-8 -> 2.  所以是： i/3
    // 再看列j: 0-2 -> 0, 3-5 -> 1, 6-8 -> 2.  所以是： j/3
    void solveSudoku(vector<vector<char>>& board) {
        //将所有位置均清空，即标记为未被填写
        memset(row,false,sizeof(row));  //清空行
        memset(col,false,sizeof(col));  //清空列
        memset(ceil,false,sizeof(ceil));  //清空3X3小方格
        //先遍历一遍九宫格, 将已经填入的数记录到记忆数组中
        for(int i=0;i<9;i++){
            for(int j=0;j<9;j++){
                if(board[i][j]!='.'){   //只要这个位置不是空格
                    int t=board[i][j]-'1';  //求出这个位置上的数字t。 t: '1' - '1' = 0。将1-9映射到0-8
                    //下面我们就需要将数字t对应的行，列，3X3小方格均标记为不能再填写该数字，即标记为true
                    row[i][t]=col[j][t]=ceil[i/3][j/3][t]=true; //标记为true，表示之后第i行，第j列，第（i/3,j/3）个3X3小方格之后不能再放数字t
                }
            }
        }
        dfs(board,0,0); //从数组的最左上角位置(0,0)开始递归。因为题目不要求我们返回数据，所以这里只需要执行一下dfs函数即可，不需要返回值
        //那么dfs函数不写返回boolean，而是写void可以吗？答案显然是不行的，因为我们需要在dfs函数中有返回值，用于结束递归
    }
    bool dfs(vector<vector<char>>& board,int x,int y){  //编写递归函数，参数：board表示题目所给数组，因为是局部变量，所以我们在递归函数中传入
    //x表示判断位置的横坐标，y表示当前判断位置的纵坐标，返回值为bool，表示当前位置能否填写，如果可以返回true，继续下一个位置的递归，如果不可以返回false，及时终止本次递归，注意回溯。
    //为了方便，我们这里让纵坐标移动
    if(y==9) x=x+1,y=0; //如果纵坐标已经越界，我们让行号加一，纵坐标去第一列
    if(x==9) return true;   //如果横坐标已经越界，说明我们已经找到了答案，返回true
    if(board[x][y]!='.') return dfs(board,x,y+1);   //如果说当前位置不是空格，我们就判断下一个位置（注意是return dfs(board,x,y+1），上面已经说了，我们每次是让纵坐标移动
    //否则的话，说明当前位置是空格，即是空格，我们就需要枚举一下看当前位置可以填写哪些数
    for(int i=0;i<9;i++){
        if(!row[x][i]&&!col[y][i]&&!ceil[x/3][y/3][i]){ //如果数在当前行，当前列，当前3X3小方格均不冲突，我们就在(x,y)填写该数，
            board[x][y]='1'+i;  //注意这里填写数字的时候要加‘1’
            row[x][i]=col[y][i]=ceil[x/3][y/3][i]=true; //填写完之后将数字对应的当前行，当前列，当前3X3小方格均标记为已出现
            //接下来继续往下一个位置递归
            // 如果下面搜索后是对的，就提前返回，不恢复现场(因为要修改board);
                // 如果是false就恢复现场（这个方法很巧妙）
            if(dfs(board,x,y+1)==true) return true; //全部填写结束，并且结果为true，说明我们已经找到了答案，返回true即可
            //否则的话，说明此路不通，我们需要恢复现场。
            //回溯之前需要恢复现场(就是变回去，即让board[x][y]重新等于'.',让数i的当前行，当前列，当前3X3小方格均恢复为false)。
            board[x][y]='.';    //让board[x][y]重新等于'.'
            row[x][i]=col[y][i]=ceil[x/3][y/3][i]=false;    //让数i的当前行，当前列，当前3X3小方格均恢复为false 
        }
    }
    //如果上面的for循环没有解，说明无解，返回false即可
    return false;   //此句可能会执行，因为在递归的过程中，我们可能会出现冲突的情况，出现冲突我们就返回false，提前结束递归。
    }
};

2021年8月25日10:59:10：

//题目保证了有且仅有一个解，我们使用dfs递归解决，我们枚举每一个格子，如果这个格子已经有数，我们就先不管，如果没有数我们就需要枚举一下这个位置上可以填哪些数，
//当然了枚举的时候不能填已经有的数，我们开数组记录每一行，每一列，以及每一个3X3的小方格中填了哪些数，
//时间复杂度：
class Solution {
    boolean[][] row=new boolean[9][9],col=new boolean[9][9]; //row记录每一行中1-9有没有出现过，col记录每一列
    boolean[][][] cell=new boolean[3][3][9]; //因为cell是三维数组，所以我们不能和上面两个二维数组放到一起申请初始化
    //cell是记录每一个3X3的小方格中1-9有没有重复出现过，默认都是false，所以我们不需要初始化,
    //注意数组row和col的第一个9代表9行或9列，第二个9代表0-8这9个数是否出现过，cell的前两维代表是哪一个方针，9代表0-8这9个数是否出现过
    public void solveSudoku(char[][] board) {
        for(int i=0;i<9;i++){   //遍历一下棋盘，把已经填过的位置更新为true
            for(int j=0;j<9;j++){
                if(board[i][j]!='.'){
                    int t=board[i][j]-'1';  //先把这个数找出来，即把字符'1'-'9'映射成数字0-8
                    //把相应行，列，3X3小方格 对应的0-8更新为true
                    row[i][t]=true; //把相应行的这个数t更新为true，即表示数t在这一行中已经出现，
                    col[j][t]=true; //把相应列的这个数t更新为true，即表示数t在这一列中已经出现，
                    cell[i/3][j/3][t]=true; //把小方针中的这个数t更新为true,表示这个数在这个小方阵中已经出现过
                }
            }
        }

        dfs(board,0,0); //我们从数组board的左上角位置开始遍历，如果有重复元素，就会结束递归，当然题目已经保证有唯一解，并且题目返回为空，所以我们只需要填好数独即可
        //因为题目不要求我们返回数据，所以这里只需要执行一下dfs函数即可，不需要返回值
        //那么dfs函数不写返回boolean，而是写void可以吗？答案显然是不行的，因为我们需要在dfs函数中有返回值，用于结束递归
    }

    public boolean dfs(char[][] board,int x,int y){  //编写外部dfs函数,注意返回值是布尔值，这样表示是否已经填好这个9宫格
        if(y==9){ //当遍历完当前行的最后一列的话，我们就换到下一行，同时让y=0，即开始遍历下一行的第一列
            x++;
            y=0;
        }
        if(x==9) return true; //当遍历完最后一行（注意是遍历完，即x=9）的话，我们直接结束递归，返回true
        
        //否则就开始正常的填写数独的过程
        if(board[x][y]!='.') return dfs(board,x,y+1);  //如果当前这个位置已经填过数了，我们直接填写下一个位置上的数，注意下一个位置是x不变，y加一
        //注意这里如果当前位置已经填过数，我们应该继续往下一个位置递归填数，注意要写上return,因为我们要继续一直往下一个递归，因为可能不止当前位置上填过数了，
        //下一个位置或者下下一个位置或者下下下一个位置.....都已经填过数了，所以我们要一直往下递归，即要加上return, 不加就是错误的
        //否则当前位置上是没有数的，我们就要枚举一下当前这个位置可以填哪些数，即枚举0-8这9个数是否在这一行，这一列，当前9宫格是否出现过
        for(int i=0;i<9;i++){ //枚举0-8这9个数是否可以填写到当前位置上，
            if(!row[x][i]&&!col[y][i]&&!cell[x/3][y/3][i]) {  //如果这个数i在当前行，列，9宫格均没有出现过，我们就把当前位置上的数填上i
            //注意填的是字符，并且是从1开始到9，即是我们要让i加上+'1'
            board[x][y]=(char)(i+'1');  //将这个数填到当前这个位置上，注意我们这里是把一个数字转为字符，可能存在溢出问题，所以需要我们进行强转
            row[x][i]=col[y][i]=cell[x/3][y/3][i]=true; //这里表示填过i之后，当前行，列，9宫格就有i了，
            //之后我们继续往下一个位置上进行递归，如果返回true，则表示全部填写完毕之后返回了true，注意这里的if中返回true，
            //不单单表示当前位置上的下一个位置上结果返回了true,因为这是递归，所以是表示我们一直往下递归，结果返回了true
            if(dfs(board,x,y+1)) {
                return true; //这里是继续往下一个位置递归，因为是递归，所以不单单表示当前位置的下一个位置
            }
            //而是一直递归到了x==9，期间一直没有返回false,只要有一个格子中返回了false,这里的if语句中就不会返回true

            //否则上面的if语句中就是返回了false，我们需要恢复现场，注意那里改变的格子上的数，就在哪个位置上填写回溯语句，这个题目就要在这里写
            //恢复现场，很重要，千万不要忘了写
            board[x][y]='.';  //将当前这个位置上恢复为'.'
            row[x][i]=col[y][i]=cell[x/3][y/3][i]=false;  //将布尔数组恢复为false
            }
        }
        //System.out.println("******"); //这里如果我们写一条输出语句，执行样例1会发现这条语句会被输出4000多行，即下面的return false会被执行很多很次，即一直在试探是否可行
        return false; //如果最后当前位置上的所有数填完之后都没有返回true,表示当前分支无解，我们返回false,对应着上面的if(dfs(board,x,y+1))
    }
}

2021年10月28日14:52:14：

class Solution {
    boolean[][] row=new boolean[9][9],col=new boolean[9][9];
    //我们填的数字是1~9，但是在数组中我们使用的是0~8,是为了和下标对应起来
    boolean[][][] cell=new boolean[3][3][9];
    //注意这里的小方格的映射，这里表示的是第[x/3,y/3]个box是否出现过数字u(0~8),
    //注意这里的表示的第[x/3][y/3]个小方格
    //9X9的大方格中的所有的3X3的小方格是:
    //00 01 02
    //10 11 12
    //20 21 22,我们发现正好就是x/3,y/3得到的

    public void solveSudoku(char[][] b) {
        for(int i=0;i<9;i++){
            for(int j=0;j<9;j++){
                if(b[i][j]!='.'){
                    int t=b[i][j]-'1';
                    row[i][t]=col[j][t]=cell[i/3][j/3][t]=true;
                }
            }
        }
        dfs(b,0,0);
    }

    public boolean dfs(char[][] b,int x,int y){ //注意这个题目我们为了知道在结束递归的时候直接返回，而不会继续往下递归，我们的dfs函数的返回值设置为布尔值
        if(y==9){
            y=0;
            x++;
        }
        if(x==9) return true;   //填完了就返回true，及时结束递归，防止之后的语句再改变了b数组
        if(b[x][y]!='.') return dfs(b,x,y+1); //如果已经填过数字了，我们就不用管这个位置继续往下递归即可
        //否则就说明这个位置还没有填过数字，我们就枚举一下当前位置可以0~8的哪一个数字
        for(int i=0;i<=8;i++){
            if(!row[x][i]&&!col[y][i]&&!cell[x/3][y/3][i]){
                b[x][y]=(char)('1'+i);
                row[x][i]=col[y][i]=cell[x/3][y/3][i]=true;
                if(dfs(b,x,y+1)==true) return true;
                b[x][y]='.';
                row[x][i]=col[y][i]=cell[x/3][y/3][i]=false;      
            }
        }  
        return false;   //这句话可能会执行，因为可能会无解，而且也需要一个return语句 
    }
}

39. 组合总和

和40异：这个题目不包含重复元素，并且每个元素可以用不限次，
同：每个数包括target都是正整数
类似于完全背包问题。

给定一个无重复元素的数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的数字可以无限制重复被选取。

说明：
所有数字（包括 target）都是正整数。
解集不能包含重复的组合。

示例 1：

输入：candidates = [2,3,6,7], target = 7,
所求解集为：
[
  [7],
  [2,2,3]
]

示例 2：

输入：candidates = [2,3,5], target = 8,
所求解集为：
[
  [2,2,2,2],
  [2,3,3],
  [3,5]
]
 

提示：

1 <= candidates.length <= 30
1 <= candidates[i] <= 200
candidate 中的每个元素都是独一无二的。
1 <= target <= 500

爆搜：核心问题是搜索顺序，我们应该考虑的是按照什么样的顺序搜索使得结果不重不漏。要记得归类搜索顺序。这个题目是从前往后搜索，然后枚举这个数选择多少个。 把方案记录下来，注意要恢复现场操作。

注意：这里不同于n皇后问题，这里是修改原数组（修改成一种可行解即可），而皇后问题是输出结果，不是修改原数组

代码：

class Solution {
public:
    vector<vector<int>> ans;    //定义全局答案数组，
    vector<int> path;   //定义全局方案数组，
    vector<vector<int>> combinationSum(vector<int>& c, int target) {
        dfs(c,0,target);    //下面需要编写递归函数，从第0个数开始，当前需要凑的值仍为target，
        return ans; //递归完成之后，返回答案数组
    }
	//dfs暴搜一遍，传入数组，当前枚举到第几个数了，需要凑的值
    void dfs(vector<int>& c,int u,int target){  //递归函数，第一个参数为数组，第二个参数u为当前枚举到了第几个数，第三个参数为当前剩余的需要凑的数
    	//每次的target都会减去前一个数，所以当target减到0说明已经找到了一组解
        if(target==0) { //如果需要凑的数为0了，说明我们已经找到了一组答案，就把这个答案放到答案数组里面
            ans.push_back(path);   //把当前方案数组放到答案数组
            return; //结束循环。
        }
        //如果枚举完了所有的数还是没有凑出target，说明无解，直接return
        if(u==c.size()) return; //如果我们已经枚举完了最后一个数，但是target还没有为0(根据没有执行上面一句if判断就可以判断出来此时target还没有为0）。还想继续枚举下一个数，说明无解，结束本次递归即可
        //下面我们就需要枚举一下当前数选择几个。
        //枚举一下当前的数可以选几个,可以选0个，或者最多选i个，且总和不超过target的个数
        for(int i=0;c[u]*i<=target;i++){    //i是代表当前数c[u]在此时这种方案中的个数，c[u]个数最多要使得之和不能超过target
        	//最开始for循环选择0个c[u]，我们不需要把c[u]放到方案中，直接往下一个数递归即可
        	//往数组下一个数递归，注意要减去c[u]*i
        	//第一次选了0个，也就是什么都没选，所以直接dfs下一个
            dfs(c,u+1,target-c[u]*i);   //一开始i等于0，即当前这个数一个都没有，我们就继续递归到下一个数，第二次枚举的时候选1个，第三次枚举的时候选2个，......
            //把选的元素加到答案中
            path.push_back(c[u]);   //选取几个加到数组中几个当前数。
        }
        //最后再恢复现场即可
        for(int i=0;c[u]*i<=target;i++){
            path.pop_back();    //每次递归添加了几个c[u],就把几个c[u]清空。
        }
    }
};

2021年8月25日12:27:14：

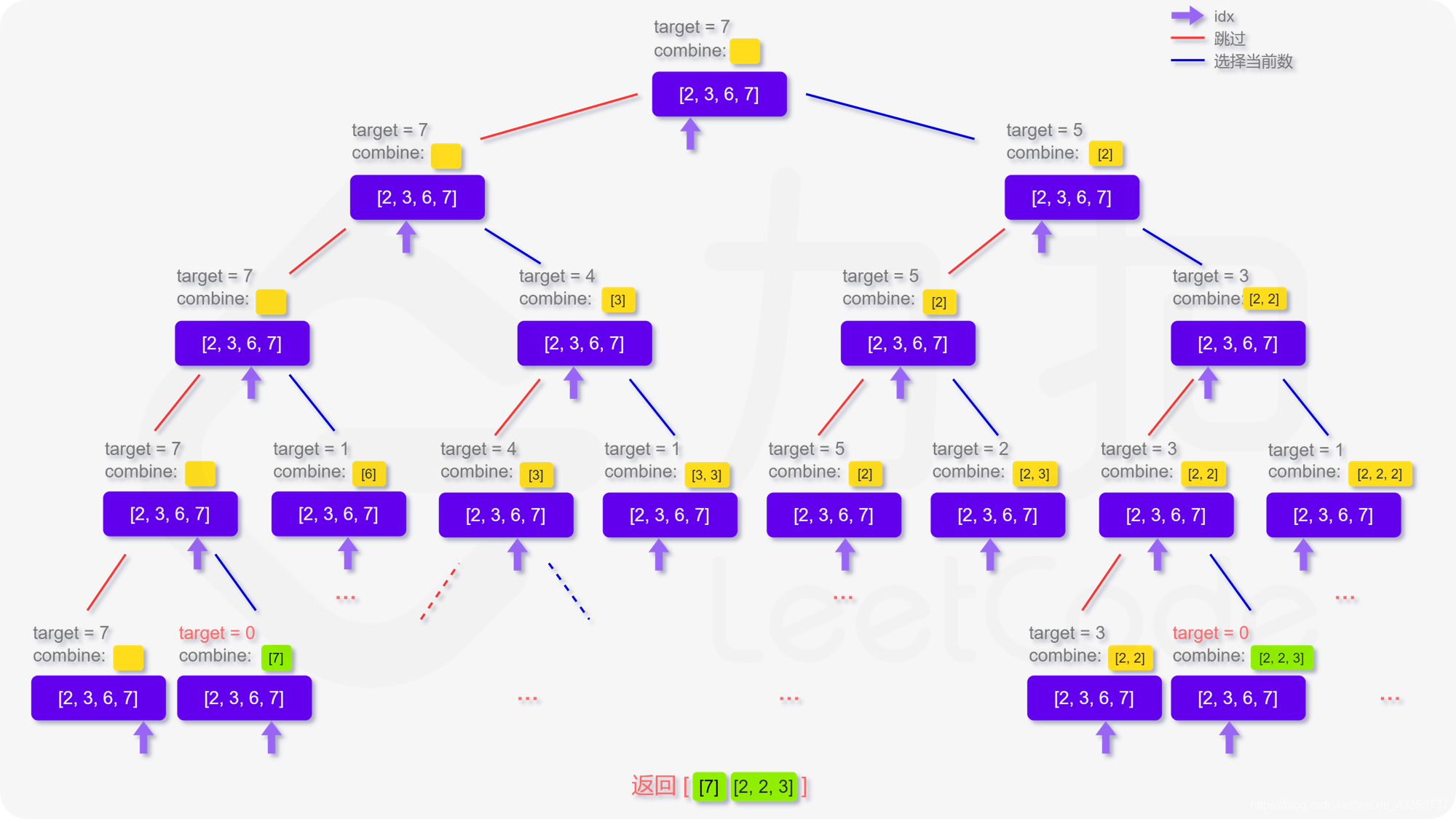
时间复杂度是指数级别的。

//注意这个题目中数组nums中元素是不重复的，但是数组中的元素可以被无限制重复地选取，并且数组中的所有数和target都是正数
//我们使用爆搜，我们在爆搜的时候，考虑按照什么样的顺序进行搜索可以不重不漏，这个题目我们从前往后看一下每一个数选多少个，
class Solution {
    List<List<Integer>> res=new ArrayList<>();  //res记录答案
    List<Integer> path=new ArrayList<>(); //path记录当前路径,path是全局的，所以记得要回溯操作
    public List<List<Integer>> combinationSum(int[] nums, int target) {
        dfs(nums,0,target); //从数组的下标0号元素开始递归，当前要凑出来的数是target，
        return res; //最后递归全部结束之后我们返回res
    }
    public void dfs(int[] nums,int u,int target){ //编写外部dfs函数，u表示当前枚举到数组的哪一个下标了，第三个参数target表示当前要凑出来的数是多少
        //当target变到了0，表示我们此时找到了一组合适的数字组合path，我们将path加到答案中
        if(target==0){
            res.add(new ArrayList<>(path));	//把当前路径上的答案加到数组中，
            //注意要写上new ArrayList<>(),Java对象是引用，不给他包裹一层，你res里存的全是同一个引用，你下次修改path里内容的时候，会给res里答案一起修改,因为下面的remove操作会将path变成空，所以如果不写new ArrayList<>,最后返回的都是空
            return; //注意这是递归，我们要写递归结束语句，即使是只有一条空语句return;也要写上
        }
        //注意if(u==nums.length) return;这个语句不能写到if(target==0)这个语句的上面，否则最后一组答案将不会被加到答案中
        if(u==nums.length) return;  //执行到这里表示target还没有凑到0.并且数组中的数字已经全部被枚举完了，即枚举完了数组中的最后一个数，我们也要结束递归
        //上面两个语句也是一次递归的结束条件。否则我们就开始枚举当前位置上的数nums[u]可以选几个,记得下面要有清空操作
        for(int i=0;nums[u]*i<=target;i++){ //i表示当前位置上的数nums[u]可以选几个，最少选0个，最多选的nums[u]的个数的数值之和不能超过target
            dfs(nums,u+1,target-nums[u]*i); //每选择一个就是一种新的情况，就要继续往下一位递归，最开始nums[u]选了0个，即nums[u]一个都没有选，注意哈，往下一位递归，下标要加一，并且target要减去对应个数的nums[u]的值
            //那么我们就往一位递归，之后是选1个nums[u]，我们就往path中加入一个nums[u],所以我们把dfs语句放到path.add(nums[u])的上面就实现了选零个nums[u]时不往path中加nums[u]的操作
            //选一个nums[u]就往path中加入一个nums[u],选两个nums[u]就往path中加入两个nums[u]......
            path.add(nums[u]);  //把上面的dfs当做一条普通的语句，这里每执行一次，就往path中加入一个nums[u]
        }
        //下面进行回溯的操作，即从path中去掉上面加入的nums[u]
        //枚举完nums[u]的所有可能的选取个数的情况，我们记得要回溯，即往path中加入几个nums[u]就要去掉几个nums[u]
        for(int i=0;nums[u]*i<=target;i++){ //加了几个nums[u]就要去去掉几个nums[u]
            path.remove(path.size()-1);
        }
    }
}

wzc助教写的两种答案，一种是传递的引用，不需要回溯，一种是copy，

(递归枚举)

1. 在每一层搜索中，枚举这个数字添加几次。
2. 搜索的终止条件是层数超过的数组的长度或者当前数字组合等于目标值。
3. 剪枝：可以先将数组从小到大排序，搜索中如果 sum != target 并且 sum+candidates[i] > target，则可以直接终止之后的递归，因为之后的数字都会比 candidates[i] 大，不会再产生答案。

class Solution {
public:
    void solve(int i, vector<int>& candidates, int sum,
             vector<int> ch, int target, vector<vector<int>>& ans) {
        // 注意这里的 ch 不是传递的引用，而是拷贝，因为在每一层需要枚举添加数字。
        if (sum == target) { // 找到目标值，添加答案。
            ans.push_back(ch);
            return;
        }
        if (i == candidates.size()) // 超出范围回溯。
            return;

        if (sum + candidates[i] > target) // 剪枝优化。
            return;

        while (sum <= target) { // 枚举使用当前数字多少次，注意可以使用 0 次。
            solve(i + 1, candidates, sum, ch, target, ans);
            sum += candidates[i];
            ch.push_back(candidates[i]);
        }
    }

    vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
        vector<vector<int>> ans;
        sort(candidates.begin(), candidates.end());
        vector<int> ch; // ch 记录已选择的数字。
        solve(0, candidates, 0, ch, target, ans);

        return ans;
    }
};

class Solution {
public:
    void solve(int i, vector<int>& candidates, int sum,
             vector<int> &ch, int target, vector<vector<int>>& ans) {
        // 注意这里的 ch 是引用。
        if (sum == target) { // 找到目标值，添加答案。
            ans.push_back(ch);
            return;
        }
        if (i == candidates.size() || sum > target) // 超出范围回溯。
            return;

        solve(i + 1, candidates, sum, ch, target, ans);

        ch.push_back(candidates[i]);
        solve(i, candidates, sum + candidates[i], ch, target, ans);
        ch.pop_back();
    }

    vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
        vector<vector<int>> ans;
        sort(candidates.begin(), candidates.end());
        vector<int> ch; // ch 记录已选择的数字。
        solve(0, candidates, 0, ch, target, ans);

        return ans;
    }
};

2021年10月22日18:55:29：

class Solution {

//首先搞懂题目:这个题目是让我们从一个无重复元素的数组num数组中,找到所有值之和为target的组合的所有方案,数组中的元素可以无限制使用多次
//乍一看这个题目好像是完全背包问题,但是因为这个题目要求我们返回所有的具体的方案,所以我们不应该使用dp,而是应该直接dfs爆搜
//因为这个题目要求我们输出所有具体的方案,所以我们不用考虑什么优化,直接爆搜就可以了,最多加上一些剪枝的操作
//爆搜的核心问题就是爆搜的搜索顺序的问题,即怎么样搜索才可以不重不漏的搜索出来所有方案,比如这个题目,我们可以从前往后看每一个数选多少个
//比如数组[2,3,6,7],我们先看第一个数,选0个,选1个,选2个,...,之后再在第一个选的个数的基础上再看第二个数选0个,1个,2个,...
//注意这里由于有总和不超过target的限制,所以每一个数的选取是有限制的而不是无限多个,因为数值都是正数,所以我们在搜索的过程中要保证不能超过target,
//所以这个搜索就很简单(y总原话),从往前后枚举每一个数选几个,在枚举的过程中记录一下方案
//所以这个题目我们在dfs函数中就需要传递的参数有,当前需要凑的值(我们每凑一个数就从target减去这个数的值),以及当前枚举到了num数组的第几位数

    List<List<Integer>> res=new ArrayList<>();
    List<Integer> path=new ArrayList<>();   //path记录当前路径
    int[] num;
    int n;
    public List<List<Integer>> combinationSum(int[] nums, int target) {
        num=nums;
        n=num.length;
        dfs(0,target);  //当前枚举到了num数组的第0位,当前需要凑的值是target
        return res; //递归全部结束之后返回答案数组res
    }
    public void dfs(int u,int target){  //在dfs的过程中,完成组合的选取,u是当前枚举到了num数组的第几位数字了,target是当前需要凑的值
        if(target==0){  //注意这里不需要u==n,只需要target=0就说明我们已经找到了一组合法的解,我们就把path加到res中
        //一定要注意这里和其他的dfs题目不一样,这里不需要枚举到num数组的最后一个数才行,前面的数字凑到target也可以,所以这里只需要target=0就可以了
            res.add(new ArrayList<>(path));
            return;
        }
        //这个和下面的if(u==n) return;是两个递归结束的条件
        if(u==n) return;  //如果我们已经枚举完了数组num的最后一个数，却还没有凑出来target(因为上面的if语句没有执行,所以target它没有凑出来)
        //而又有其枚举完了最后一个数(满足了u==n),就说明当前路径是无解的,我们直接return结束递归,即剪枝的操作

        //再否则我们就来枚举一下当前这个数选几个
        for(int k=0;num[u]*k<=target;k++){  //k枚举的是当前这个数num[u]选几个,可以选0个,所以k从0开始,但是要保证选当前数的个数最多总和不能超过target，k是枚举的个数
        //注意要搞清楚或者说记得k枚举的是当前数字num[u]的选取个数,不是num数组的选取的下标
            dfs(u+1,target-k*num[u]); //当选取0个num[u]的时候,即没有选取num[u],所以我们不能往path中添加num[u]
            //当不选num[u]的时候(k=0),我们应该继续看下一个数,即往u+1位置上递归,并且target要减去选取的num[u]的值之和
            path.add(num[u]); //当递归结束的时候我们再往path中添加num[u],选几个num[u]就把几个num[u]加到path中
            //这样我们把dfs放在path.add(num[u])的上面的操作就实现了当没有添加num[u](k=0)的时候,我们直接往下一个数递归搜索
        }
        //上面我们把path放到dfs的后面就实现了第一次选取0个num[u]的时候,一个num[u]也没有添加到path中,第二次选取1个num[u]的时候,添加一个num[u]到path中

        //下面记得回溯操作,即恢复现场,我们添加了几个num[u]就要回溯几次,即从path中删除几个数,框架和上面的代码差不多
        for(int k=0;num[u]*k<=target;k++){  //恢复现场：即把这一次调用的枚举全部撤销掉之后再返回
            path.remove(path.size()-1); //上面的dfs的操作只是往path中添加了元素(添加的元素个数是不一样的),所以我们回溯的时候也只需要删除元素
        }
    }
}

方法二：

class Solution {
    List<List<Integer>> res=new ArrayList<>();
    List<Integer> path=new ArrayList<>();
    int[] c;
    int n;
    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        c=candidates;
        n=c.length;
        dfs(0,target);
        return res;
    }
    public void dfs(int u,int target){
        if(target==0) {
            res.add(new ArrayList<>(path));
            return;
        }
        //方法二：枚举数组中的每一个数
        for(int i=u;i<n;i++){
            if(target-c[i]>=0){ //只要targer-c[i]>=0,我们就可以添加c[i]
                path.add(c[i]); //只要可以添加c[i],我们就添加c[i],
                dfs(i,target-c[i]); //继续往下递归，注意这里递归的下标是i,不是u,并且我们添加了一个c[i],所以我们要从target中减去一个c[i]，并且注意是i，不是i+1,因为我们现在可能还可以添加c[i]的
                path.remove(path.size()-1); //dfs结束回溯的时候，我们因为添加一个c[i]，所以这里我们要去除
            }
        }
    }
}

39. 组合总和 40. 组合总和 II 46. 全排列 47. 全排列 II 77. 组合 78. 子集 90. 子集 II 经典的dfs的问题：

39，40, 90题都是组合问题，代码都很类似，
46,47,77题是排列问题，代码比较类似

搜索组合和搜索排列是不同的,
所有组合类型的题目的代码都是很相似的，

40. 组合总和 II

和39异：这个题目包含重复元素，并且每个元素只能用一次，（但是如果有5个3，则3最多可以用5次）
同：每个数包括target都是正整数
类似于多重背包问题。

给定一个数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的每个数字在每个组合中只能使用一次。

说明：

所有数字（包括目标数）都是正整数。 解集不能包含重复的组合。

示例 1:

输入: candidates = [10,1,2,7,6,1,5], target = 8,
所求解集为:
[
  [1, 7],
  [1, 2, 5],
  [2, 6],
  [1, 1, 6]
]

示例 2:

输入: candidates = [2,5,2,1,2], target = 5,
所求解集为:
[
  [1,2,2],
  [5]
]

这个题目和39题不同的是：数组中的元素不是独一无二的，且数组的数最多只能使用一次，且集合中的解集不能重复。这个题目在枚举元素的时候，不仅被总和限制还被元素的个数限制。（如一个数只有5个，你最多只能枚举5个这个数，不能枚举6个甚至更多，这个题目在枚举的时候需要再加一个个数的限制条件。）
这个题目需要先排序，这样就可以很方便的计算出每个元素的个数（或者使用哈希表也可以），

算法分析
dfs + 排序

• 1、为了避免选择了重复的元素，先对数组有规则的进行排序，例如从小到大排序
• 2、当枚举到某一位置时，找到相同的元素区间[u,k -1]，共cnt个可以选，暴力枚举每个数字选多少个
• 3、当枚举到的总值sum > target，表示该枚举方式不合法，直接return
• 4、当枚举完每个数字之后，若sum == target，表示该选择方案是合法的，记录该方案(不到target,则需要继续往后枚举）

注意:枚举的时候的小细节，枚举每个数字选多少个的时候，本来是枚举多少个，最后dfs下一层完后，就应该全部恢复现场，删除多少个，再枚举下一种情况。可以直接枚举该数字选多少个，假设最多能选t个，则每选一个dfs一次，操作了t+ 1次之后，再把这t个相同的数字一次性恢复现场 (y总的小技巧)

加入了元素个数的限制，即有限背包的问题，我们在递归的时候，不仅要限制总和不能超过target，而且还要保证加的每一个元素个数总数不能超过其总的个数。

代码：

class Solution {
public:
    vector<vector<int>> ans;    //定义全局答案数组
    vector<int> path;   //定义方案数组
    vector<vector<int>> combinationSum2(vector<int>& c, int target) {
    	//排序，方便枚举每一段,//排序目的：1.去重复 2.剪枝提速
        sort(c.begin(),c.end());    //对数组排序，方便计算每个数出现的个数。
        dfs(c,0,target);    //从第0个数开始递归，且此时需要凑的数值就是target。
        return ans; //将答案数组返回。
    }
    void dfs(vector<int>& c,int u,int target){  //编写递归函数，u是遍历到第几个数，target是当前需要凑的值
        if(target==0){		 //回溯点
            ans.push_back(path);    //如果当前需要凑的数target为0了，说明我们此时找到了一组答案。
            return; //结束每次递归
        }
        if(u==c.size())return;  //如果遍历完最后一个数仍没有凑出来target，说明无解，我们直接结束即可。
        //下面我们就需要开始枚举当前数了，我们需要先在排好序的数组中数出来当前数的个数，
        //找到每一段的起始
        int k=u+1;  //从第u+1个数往后数一下一共多少个数和当前数c[u]相同，一开始就1个 
        while(k<c.size()&&c[k]==c[u])k++;   //往后遍历,最后时k到达了第一个大于c[u]的位置；
        //每一段有cnt个相同的数，枚举的个数不能超过cnt
        int cnt=k-u;    //c[u]的个数(k-1-u+1=k-u)
        //枚举一下当前的数可以选几个,可以选0个，或者选i个总和不超过target的个数并且不能超过cnt个
        for(int i=0;c[u]*i<=target&&i<=cnt;i++){    //这里不仅需要总和<=target，还需要个数不能大于cnt个,这里的i是指的个数，不是指下标）
         	//跳到下一个不同的数字,下一个数开始应该是k开始
            dfs(c,k,target-c[u]*i);     //继续对下一个数进行递归，此时k的位置就是下一个不同于c[u]的位置(注意是k,不是u+1,因为此时下一个数是从k开始的，不是u+1)。
            path.push_back(c[u]);   //每枚举一个当前数c[u]，就压入一个c[u]到方案数组中。
        }
		//恢复现场
        for(int i=0;c[u]*i<=target&&i<=cnt;i++){    //记得恢复现场。
            path.pop_back();
        }
    }
};

2021年8月25日15:25:08：

//这个题目和上个题目的区别就是数组中的每一个数字都只能使用一次，但是数组中可能有重复元素,即这个题目限制了我们每个数最多可以选几次
//这个题目和上面题目的区别就是在for循环中再加上一个个数的限制即可，其他算法和上一个题目基本上完全相同，
//为了方便的计算出来每一个数的个数有多少个，并且也是为了避免重复枚举我们这里使用sort对数组先做一个排序，注意nlogn的复杂度在指数级别的爆搜目前不值一提，
//或者使用哈希表来记录数的个数，但是注意使用哈希表如果不对数组进行排序的话，可能存在重复枚举的问题
class Solution {
    List<List<Integer>> res=new ArrayList<>();  //定义答案数组
    List<Integer> path=new ArrayList<>(); //定义当前路径
    public List<List<Integer>> combinationSum2(int[] c, int target) {
    	//注意注意注意数组是没有排好序的，而这个题目我们需要一个有序的数组，以便于计算相同数的个数以及避免重复枚举
        Arrays.sort(c); //先对数组进行排序，使得相同数都排在一起
        dfs(c,0,target);  //从数组的下标0开始爆搜，当前需要凑出来的数是target
        return res; //最后递归结束返回res答案
    }
    public void dfs(int[] c,int u,int target){
        if(target==0){
            res.add(new ArrayList<>(path));
            return;
        }
        if(u==c.length) return;
        //下面我们需要数一下当前这一段的nums[u]有几个，注意nums[u]是当前这个数的第一个元素,我们这里使用双指针来求一下当前这个数的个数
        int k=u+1;  //k用来计算当前这个数的个数
        while(k<c.length&&c[k]==c[u]) k++;  //当k停下来的时候，k是下一段的第一个数，k-1就是最后一个等于c[u]的位置，即当前c[u]的个数是k-1-u+1=k-u个
        int count=k-u;  //count即是当前c[u]的个数
        for(int i=0;(c[u]*i<=target)&&(i<=count);i++){  //注意这里不仅要满足c[u]*i<=target,同时也要满足i<=count，注意i是枚举的c[u]的个数，不是下标，所以可以等于target,
        //如果不写等于targe的话，那些只有一个的元素将不会被枚举到，即得到错误的答案
            dfs(c,k,target-c[u]*i); //注意这里下一段的第一个数不是u+1,而是k,所以这里不要写成u+1,而是k
            path.add(c[u]);
        }

        //回溯
        for(int i=0;(c[u]*i<=target)&&(i<=count);i++){
            path.remove(path.size()-1);
        }
    }
}

2021年10月22日18:55:39：

class Solution {

//这个题目和39题不一样的题目在于：num数组中的数字是有重复的，并且每个数字只能被用一次，即相当于这个题目告诉了我们每个数最多可以选几次，
//如果说是一个题目是类似于完全背包问题，那么这个题目就相当于是多重背包问题，这个题目不仅要被总和限制还需要被个数限制,比如一个数只有5个，那这个数最多枚举5个，
//即在上一个题目的基础上，再枚举个数的基础上再加一个个数的限制就可以了，其他和上个题目的代码基本上相同，
//这个题目为了方便计数相同数字的个数，我们可以对数组排个序，因为排序之后相同数会挨在一起，我们再使用指针扫描记录相同数字的个数即可，
//即这里为了避免选择了重复的元素，先对数组有规则的进行排序，例如从小到大排序，当枚举到某一位置的时候，找到相同的元素区间[u,k-1],
//则当前元素有cnt=k-1-u+1=k-u个可以选用，我们就暴力枚举每一个数字选多少个，最多枚举个数有两个限制：1.不能超过cnt,2.总和<=taget
//注意：枚举的时候的小细节，枚举每个数字选多少个的时候，本来是枚举多少个，最后dfs下一层完后，就应该全部恢复现场，即要删除多少个，再枚举下一种情况。
//这里可以直接枚举该数字选多少个，假设最多可以选t个，则每选一个dfs一次，操作了t+1次之后，再把这t个相同的数字一次性恢复现场

    List<List<Integer>> res=new ArrayList<>();
    List<Integer> path=new ArrayList<>();
    int[] num;
    int n;
    public List<List<Integer>> combinationSum2(int[] nums, int target) {
        Arrays.sort(nums);  //先将数组排序，这一步是地基，是之后所有操作的基础，没有对数组排序，一切都是白谈。
        num=nums;
        n=num.length;
        dfs(0,target); //从num数组的下标为0的位置开始递归，当前需要凑的数是target
        return res; //递归结束返回答案数组
    }
    public void dfs(int u,int target){ //在dfs的过程中完成寻找组合的过程，u是当前枚举到了num数组的下标位置，target是当前需要凑的值
        if(target==0){  //当target为0了，就说明我们找到了一组解，
            res.add(new ArrayList<>(path)); //我们将path加到res中
            return;
        }
        if(u==n) return; //如果我们已经枚举完了num数组中的所有数字，但是还没有凑出来target(即我们没有执行上面的if语句)，就说明当前路径不合法，我们直接return结束
        //否则我们就枚举一下当前这个数选几个，我们应该先使用双指针数一下当前数有几个
        int k=u+1;  //u是这一段的第一个数，k=u+1即这一段的第二个数的位置
        while(k<n&&num[k]==num[u]) k++; //只要num[k]和num[u]值相同，我们的k就往后走，最后k就到达了下一段的第一个的位置
        int cnt=k-1-u+1; //当前这一段数的个数是k-1-u+1=k-u个
        //这样计算完num[u]的个数之后，我们再来枚举num[u]选几个
        for(int i=0;i*num[u]<=target&&i<=cnt;i++){ //注意i在这里枚举的是当前数num[u]选几个，有两个限制:1.总和不能超过target,2.个数不能超过cnt
            dfs(k,target-i*num[u]);  //注意这里下一段的第一个数的下标是k,不是u+1了,还要注意选了几个num[u],这里就要从target中减去几个num[u]
            path.add(num[u]); 
            //这里同样，为了达到当选取0个这个数的时候我们不添加这个数的操作，我们把dfs放在了path.add()语句的上面
        }
        //回溯操作，也和39题差不多，加了几个num[u]就去除几个num[u]
        for(int i=0;i*num[u]<=target&&i<=cnt;i++){  //i这里代表的还是个数，上面添加了几个num[u],我们这里就要去除几个
            path.remove(path.size()-1); 
        }
    }
}

class Solution {
    List<List<Integer>> res=new ArrayList<>();
    List<Integer> path=new ArrayList<>();
    int[] c;
    int n;
    public List<List<Integer>> combinationSum2(int[] candidates, int target) {
        c=candidates;
        n=c.length;
        Arrays.sort(c);
        dfs(0,target);
        return res;
    }
    public void dfs(int u,int target){
        if(target==0){
            res.add(new ArrayList<>(path));
            return;
        }
        if(u==n) return;
        for(int i=u;i<n;i++){
            if(i>u&&c[i-1]==c[i]) continue; //必须要保证当前这个数是第一次被使用，否则我们就跳过这个数,这里和y总之前的"嫡长子继承制"的思想是一致的，
            if(target-c[i]>=0){ //这里的代码就和上一个题目一样了
                path.add(c[i]);
                dfs(i+1,target-c[i]);	//每一个数只能用一次，所以这里往下递归的时候是i+1
                path.remove(path.size()-1);
            }
        }
    }
}


这个避免重复当思想实在是太重要了。
这个方法最重要的作用是，可以让同一层级，不出现相同的元素。即
                  1
                 / \
                2   2  这种情况不会发生 但是却允许了不同层级之间的重复即：
               /     \
              5       5
                例2
                  1
                 /
                2      这种情况确是允许的
               /
              2  
                
为何会有这种神奇的效果呢？
首先 cur-1 == cur 是用于判定当前元素是否和之前元素相同的语句。这个语句就能砍掉例1。
可是问题来了，如果把所有当前与之前一个元素相同的都砍掉，那么例二的情况也会消失。 
因为当第二个2出现的时候，他就和前一个2相同了。
                
那么如何保留例2呢？
那么就用cur > begin 来避免这种情况，你发现例1中的两个2是处在同一个层级上的，
例2的两个2是处在不同层级上的。
在一个for循环中，所有被遍历到的数都是属于一个层级的。我们要让一个层级中，
必须出现且只出现一个2，那么就放过第一个出现重复的2，但不放过后面出现的2。
第一个出现的2的特点就是 cur == begin. 第二个出现的2 特点是cur > begin.

46. 全排列

和47.全排列II不同的地方：47题可能包含相同的元素（可包含重复数字），而46题没有重复的元素。

给定一个 没有重复 数字的序列，返回其所有可能的全排列。

示例:

输入: [1,2,3]
输出:
[
  [1,2,3],
  [1,3,2],
  [2,1,3],
  [2,3,1],
  [3,1,2],
  [3,2,1]
]

算法分析：
回溯：

算法思路
dfs + 回溯解题框架
dfs算法的过程其实就是一棵递归树，所有的dfs算法的步骤大概有以下几步：

• 找到中止条件，即递归树从根节点走到叶子节点时的返回条件，此时一般情况下已经遍历完了从根节点到叶子结点的一条路径，往往就是我们需要存下来的一种合法方案
• 如果还没有走到底，那么我们需要对当前层的所有可能选择方案进行枚举，加入路径中，然后走向下一层
• 在枚举过程中，有些情况下需要对不可能走到底的情况进行预判，如果已经知道这条路不可能到达我们想去的地方，那我们干嘛还要一条路走到黑呢，这就是我们常说的剪枝的过程
• 当完成往下层的递归后，我们需要将当前层的选择状态进行清零，它下去之前是什么样子，我们现在就要让它恢复原状，也叫恢复现场。该过程就是回溯，目的是回到最初选择路口的起点，好再试试其他的路。

将上面的算法框架应用于对于本题，根据习惯，枚举时我们可以选择每个位置放哪个数，同时也可以枚举每个数放在哪个位置。 不同枚举顺序，就会画出不同的递归搜索树（如下图），接下来我们就分别分析以下两种情况：

算法一：枚举每个位置放什么数

1. 因为我们需要枚举每个位置放什么数，因此当我们每个位置都放好数，我们就走到了递归树的叶子节点，此时将我们的该路径加入方案中。
2. 如果还没有到达叶子结点，那么我们需要枚举选择该位置放哪些数，因为我们每个数都必须用且只能用一次，所以我们利用st数组来标记那些数被用过。枚举每一个数，如果没有用过，即可加入路径并标记，然后递归到下一层，即下一个位置。
3. 递归结束后，我们需要恢复现场，消除刚才的标记，并把刚才放在该位置上的数清空，即弹出。这样做的目的是因为当前位置上还可以选择放其他数，所以需要回到往下走之前的样子，然后再选择其他路。

算法一代码：

class Solution {
public:
    vector<vector<int>> res;
    vector<int> path;
    vector<bool> st;
    vector<vector<int>> permute(vector<int>& nums) {
        st = vector<bool> (nums.size());
        dfs(nums, 0);
        return res;
    }

    void dfs(vector<int>& nums, int u) //u表示枚举到了方案数组path的哪个位置
    {
        if (u == nums.size()) //遍历完整个数组
        {
            res.push_back(path); //加入方案
            return;
        }

        for (int i = 0; i < nums.size(); i ++) //枚举当前位置可以选择哪些数
        {
            if (!st[i]) //没有选过
            {
                path.push_back(nums[i]); //选择该数
                st[i] = true; //标记选过
                dfs(nums, u + 1); //继续递归下一层
                st[i] = false; //回溯
                path.pop_back(); //回溯
            }

        }
    }
};

算法二：枚举每个数放哪个位置

1. 因为我们需要枚举每个数放什么位置，因此把所有数都放到了位置上，我们就走到了递归树的叶子节点，此时将我们的该路径加入方案中。
2. 如果还没有到达叶子结点，那么我们需要枚举当前数可以放在哪个位置，显然每个位置只能放一个数，所以我们利用st数组来标记那些位置上已经放好数了。枚举每个位置，如果没有放上任何数，即可在该位置放上数，然后递归到下一层，即继续去放下一个数。
3. 递归结束后，我们需要恢复现场，消除刚才的标记，由于只要当前位置的标记被清空，该位置就可以放数，所以当我们放下一个数时，如果发现该位置没有用过，即可放上去，此时刚好就能覆盖本来填上的数，因此位置上的数并没有必要清空。

算法分析
(DFS+回溯) O(n^2)

• 考虑在每个位置上放数字，放完就递归到下一层，在下一个位置接着放数字，直到放满位置
• 设置标记，表示哪个数被用过；如果位置放满了就记录答案

枚举每个位置当前放什么元素。st数组标记当前哪些元素被用过了，path数组存储当前枚举的路径，u代表当前枚举的元素位置。搜索时，依次将每一个没有访问过的元素加入path，修改st标记为true，递归搜索，然后恢复现场（将这个元素弹出path,恢复st标记为false）。

时间复杂度分析：O(n∗n!)，总共n!种情况，每种情况的长度为n。

代码：

class Solution {
public:
    //记录所有的方案
    vector<vector<int>> ans;    //ans数组存放答案
    //储存符合条件的数组
    vector<int> path;   //path数组记录路径
    //记录是否被访问过
    vector<bool> st; //st数组记录path数组对应下标是否存放了数
    vector<vector<int>> permute(vector<int>& nums) {
        int n=nums.size();  //n是数组长度
        path=vector<int>(n,0);  //初始化长度
        st=vector<bool>(n,false);   //初始化长度
        dfs(nums,0);   //暴搜即可，从第0 位开始,
        return ans; //递归结束返回答案
    }
    //u表示枚举到了数组中的哪个数
    void dfs(vector<int>& nums,int u){  //编写递归函数，传入参数包括输入数组nums,而u是path路径的下标
    	//遍历完整个数组
        if(u==nums.size()){ //访问到了最后的叶节点，说明找到了一组解
        	//加入方案
            ans.push_back(path);    //将这组解保存到答案中
            return; //找到就结束本次递归
        }
        //下面就是正常的递归过程
        //枚举每个位置
        for(int i=0;i<nums.size();i++){ //从前往后枚举数组中每一个数
        	//如果该位置还没有放任何数
            if(st[i]==false){   //如果当前的位置还没有被用过
                path[u]=nums[i];    //当前的数字可用,我们就让path的第u个位置值等于nums[i],注意不是add,而是将对应位置的数字改变为nums[i]。
                //记录已经访问过
                st[i]=true;    //同时记录第i个数已经被用过了,
                //dfs到下一层
                dfs(nums,u+1);
                st[i]=false;    //恢复现场(递归是什么样，恢复现场就要变成什么样)，这里我们标记该位置数还未被访问
                path[u]=0;  //因为path[u]会被nums[i]覆盖掉，所以这一步也可以不用写。
            }
            //这里else不用写即st[i]==true,st[i]=true则表示该位置已经被用过，如果被用过则我们就不能再用这个数字，所以我们这里对于else应该省略不写。
        }
    }
};

java代码：

class Solution {
    List<List<Integer>> res=new ArrayList<>();
    List<Integer> path=new ArrayList<>();
    boolean[] f;
    public List<List<Integer>> permute(int[] nums) {
        int n=nums.length;
        for(int i=0;i<n;i++){
            path.add(0);
        }
        f=new boolean[n];
        Arrays.fill(f,false);
        dfs(nums,0);
        return res;
    }
    public void dfs(int[] nums,int u){
        if(u==nums.length){
            res.add(new ArrayList<>(path));
            return ;
        }
        for(int i=0;i<nums.length;i++){
            if(f[i]==false){
                path.add(u,nums[i]);
                f[i]=true;
                dfs(nums,u+1);
                f[i]=false;
                path.set(u,0);
            }
        }
    }
}

2021年8月25日20:17:29：

//爆搜，爆搜的时候，需要保证不重不漏，全排列这个题目我们可以枚举每一个位置上填什么数字，也可以依次枚举每一个数，看这个数可以放到哪个位置上
//第一种最常见，即枚举每一个位置上填什么数字，
class Solution {
    List<List<Integer>> res=new ArrayList<>();
    List<Integer> path=new ArrayList<>();
    boolean[] st; //布尔型数组st表示nums数组中的对应位置上的数是否已经被用过，所以下面我们初始化的时候将st数组的长度初始化为nums的长度
    public List<List<Integer>> permute(int[] nums) {
        int n=nums.length;
        st=new boolean[n];  //对st数组进行初始化
        //开始递归
        dfs(nums,0);    //0表示当前枚举到第几位了
        return res; //最后递归结束，返回res即可  
    }
    public void dfs(int[] nums,int u){
        if(u==nums.length){ //当枚举完了数组nums中的每一个数，就说明我们找到了一个全排列
            res.add(new ArrayList<>(path));
            return; //递归结束语句，一定要写return;即使这里是返回的是空，也要写上return;
        }
        //否则就要枚举一下当前位置u上可以填哪些数
        for(int i=0;i<nums.length;i++){
            if(st[i]==false){ //如果nums数组的第i个位置上的数还没有被用过
                path.add(u,nums[i]);  //将数组path的第u个位置上填上nums[i],注意java中的list可以直接添加，即添加到最后，也可以指定下标位置进行添加元素，
                //这里也可以使用set解决，即是path.set(u,nums[i])
                st[i]=true; //并且标记nums数组的第i个位置上的数已经被用过了，即更新数组st[i]=true
                dfs(nums,u+1);  //继续往下递归，即填写nums数组的下一个位置上的数
                //递归完之后记得恢复现场，即回溯,恢复现场，即你做了哪些修改就要恢复回什么样
                st[i]=false;  //即重新标记数组nums的第i个位置上的数还没有被用过
                path.remove(u); //ArrayList在进行删除元素的时候只能指定下标位置进行删除，其实这步回溯可以不用写，只写st[i]=false即可，
                //因为path.add(u,nums[i])这一步保证了path的u号位置会被别的元素替代
            }
        }
    }
}

2021年10月23日14:39:34：

class Solution {

//注意排列问题和组合问题是不同的,组合问题是不强调顺序之间的顺序,即顺序不同也视为相同的方案(所以组合问题最重要的一点就是去重),
//而排列问题是强调元素之间的顺序的,即顺序不同视为不同的方案,
//因为要求出具体的所有的方案,所以我们直接使用dfs来做就可以了,最重要的是考虑按照什么样的顺序来搜,我们可以枚举每一个位置上填哪些数(排列问题都是这样考虑的),
//比如对于这个题目(即不含重复数字的),我们枚举第一个位置可以填哪些数,可以填1,2,3,比如填了1,则第二个位置可以填2,3,比如第二个位置填了2,则第三个位置只能填3了
//如果第二个位置填了3,则第三个位置只能填2了,可以画出递归树,最后每一个叶子结点都代表一种方案,刚开始学dfs的问题的时候画一颗递归搜索树很重要
//我们现在就来看一下需要在dfs的参数中传递哪些参数,(参数可以是全局的也可以是放在dfs参数中的)或者说需要记录哪些状态:
//1.首先,我们需要记录每一个位置上填什么,即需要一个path数组记录当前的路径,2.需要记录当前枚举到了nums数组中的哪一个数字了(即需要记录一个下标u)
//3.需要记录当前已经有哪些数字已经被用过了,因为是排列问题是要区分元素的顺序的,即可以从前往后枚举数字,也可以从后往前枚举数字,
//为了不重复使用同一个数字,所以我们需要一个全局的布尔状态数组st来记录当前已经用了哪些数字了,
//所以我们的dfs中需要用到这三个状态或者叫参数,而在递归树的分支的选择上,我们就可以看一下当前哪些数没有被用过,我们就可以用哪些数,即走到对应的分支上
//这个题目是不含重复元素的,而下一个题目是包含重复元素的
//组合问题是枚举的是当前数字选取几个，而排列问题枚举看的是当前path[u]上可以填写nums数组的哪一个数

    List<List<Integer>> res=new ArrayList<>();
    List<Integer> path=new ArrayList<>();
    boolean[] st;  //全局布尔数组记录数组中的每一个数字是否被用过
    int n; //n是nums数组的长度，即为全局变量，
    int[] num;  //将nums数组定义为全局的
    public List<List<Integer>> permute(int[] nums) {
        num=nums;
        n=nums.length;
        st=new boolean[n];  //初始化st数组
        dfs(0); //0表示当前要填path路径数组的哪一位数了，从第0位开始枚举看
        return res; //递归结束的时候返回答案数组res
    }
    public void dfs(int u){ //在dfs函数的递归过程中完成求取所有的排列的过程，u是当前枚举到了nums数组的第几位了
        if(u==n){   //如果已经枚举完了所有的数
            res.add(new ArrayList<>(path)); //如果已经枚举完了全部的数，即找到了一个排列，我们就将当前路径加到res数组中
            return;
        }
        //否则我们就要枚举看一下当前位置u上可以填哪些数：我们就从前往后看nums数组中的每一个数，如果这个数还没有被用，我们就可以将这个数填到位置u上
        for(int i=0;i<n;i++){ //从前往后看nums数组的每一个数，看这个数字是否被用过，如果没有我们就可以用这个数
            if(st[i]==false){ //只有当当前nums数组这个位置上的数字没有被用过(即st[i]=false)我们就可以用这个数字，
            //如果已经被用过我们就不用管它了,注意这里是下标，用下标对应到nums数组中的具体的数字
                path.add(num[i]); //当前位置上的数字没有被用过，我们就可以用当前这个位置上的数，即把nums[i]加到路径path中,
                //并把st[i]改为true,表示对应的nums数组的第i个位置上的数已经被用过了，后面就不能再用这个下标上对应的数字了
                st[i]=true;	//别忘了将st[u]标记为true,即表示nums数组的第i个位置被用了
                dfs(u+1); //填完第u个位置，我们就往下递归填第u+1个位置，注意这里就是u+1,
                //递归结束的时候需要回溯，恢复现场
                st[i]=false;  //将nums数组的第i个位置上的数字标记为没有被用过，即将st[i]改为true
                path.remove(path.size()-1); //去掉刚才添加的数字
            }
        }
    }
}

47. 全排列 II

和46.全排列I不同的地方：47题可能包含相同的元素（可包含重复数字），而46题没有重复的元素。

给定一个可包含重复数字的序列 nums ，按任意顺序 返回所有不重复的全排列。

示例 1：

输入：nums = [1,1,2]
输出：
[[1,1,2],
 [1,2,1],
 [2,1,1]]

示例 2：

输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
 

提示：

1 <= nums.length <= 8
-10 <= nums[i] <= 10

算法思路
DFS + 回溯
阅读此篇之前建议先阅读LeetCode 46. 全排列 46全排列，与上一题不同的是，该题目给的数组里面可能出现相同元素。如果根据我们上题的做法，我们可以选择每个数可以放在哪些位置，同时我们也可以选择每个位置放哪些数，然后画出以下递归搜索树。
枚举每个位置可以放哪些数
以该种枚举顺序，我们可得下图递归搜索树，我们可以看出，出现重复方案的原因是因为，当我们在枚举某一位置时，如果我们将两个1看作是不同元素，那么我们枚举时可以选择把哪个1放在该位置上.但是明显放蓝色的1和绿色的1最终的方案都是一样的，因此我们在枚举每个位置可以放哪些数时，如果下一个选择的数和当前选择的数相同，那么我们就跳过。
为了实现上述过程，我们需要将原数组中的元素进行排序，然后将原数组中元素之间的相对位置作为每一种方案中元素的相对位置。

算法
(DFS+回溯)
以[1,1,2]为例，图解如下:

这题剪枝的前提需要先排序，排序后所有相等的数全部都靠在一起

碰到重复元素会有两种情况
1.这个数正在被使用，那么下一个位置能够摆上相同的数字
2.这个数刚刚被撤销，如果下一个位置摆上刚才撤销回来的数字，那么递归树必然和撤销前的递归树重复，所以应该剪枝

时间复杂度：O(n∗n!)

代码：

class Solution {
public:
    vector<vector<int>> ans;    //ans记录答案数组
    vector<int> path;   //path记录每个位置填的数
    vector<bool> st;    //st数组记录判重数组。记录该位置是否已经记过数
    vector<vector<int>> permuteUnique(vector<int>& nums) {
    	//一定要注意先排序。
        sort(nums.begin(),nums.end());  //先对数组进行排序
        int n=nums.size();  
        path=vector<int>(n,0);    //初始化数组长度,且将所有元素初始化为0，下面我们需要将path中的元素进行覆盖更新
        st=vector<bool>(n,false);  //初始化数组长度，初始化为false,代表这个位置还没有被覆盖。
        dfs(nums,0);    //从下标0开始递归
        return ans; //返回答案
    }
    //u表示枚举到的位置
    void dfs(vector<int>& nums,int u){  //编写递归函数，传入参数：原数组，递归下标位置。
        //如果我们已经枚举完所有位置，说明我们找到了一组合法方案
        if(u==nums.size()){ //找到了一组方案
            ans.push_back(path);    //把方案放到答案数组中。
            return;
        }
        //下面就是正常递归过程，看一下当前位置可以填什么，我们就从前往后枚举一下看当前位置可以填什么
        //枚举该位置u可以放哪些数
        for(int i=0;i<nums.size();i++){ 
        	//下面这个一定要写，容易忘。
            if(st[i]==false){   //如果当前位置的数没有被用过，我们就需要考虑是否能放到下标u，如果已经被用过，则我们就没有必要考虑了，即这个if对应的else语句不用写
                //判断当前数是否可用，首先i>0,如果i=0则当前数一定是第一个数，一定没有被用过。其次这个数和前面数相同，如果不同，说明也是第一个新数，也可以用。
                //最后保证前面数还没有被用过，如果前面数用过了，则当前数也是可以用的。只有这三个条件都满足就可以跳过了。
                 //若与前一个数相等情况下前那个必须还没放进过，则表示重复
                if(i>0&&nums[i-1]==nums[i]&&st[i-1]==false)continue;  //嫡长子继承制，如果前一个相同数还没有被用过，则相同数的后一个数，就需要先等等（continue）
                //这里上面if语句就不满足了，我们就可以把nums[i]放到位置u
                path[u]=nums[i];    //把nums[i]放到path数组的位置u
                st[i]=true;   //把nums[i]标记为已用过。
                dfs(nums,u+1);  //继续往下一个位置递归
                st[i]=false;  //恢复现场
                path[u]=0;  //可写可不写。
            }
        }
    }
};

疑惑点：y总，不是很理解避免重复这里

cpp if (i && nums[i - 1] == nums[i] && !st[i - 1]) continue;

ii 不是从小到大循环的吗，对于同一个数字，i−1i−1 不应该都会比 ii 先用了吗

yxc 5个月前 回复 每次枚举用nums[i - 1]之后，会把这个数的使用状态恢复成未被使用，所以状态恢复之后在枚举nums[i]时，会发现nums[i - 1]的状态是未被使用。

class Solution {
    List<List<Integer>> res=new ArrayList<>();
    public List<List<Integer>> permuteUnique(int[] nums) {
        Arrays.sort(nums);	//一定要注意先排序。
        int n=nums.length;
        Integer[] path=new Integer[n];
        Arrays.fill(path,0);
        boolean[] st=new boolean[n];
        Arrays.fill(st,false);
        dfs(nums,0,path,st);
        return res;
    }
    public void dfs(int[] nums,int u,Integer[] path,boolean[] st){		//这里在编写dfs的时候，我们因为要使用局部变量，所以这里我们把局部变量作为参数传入dfs函数
        if(u==nums.length){
            List p=Arrays.asList(path);	//将数组转为数组列表
            res.add(new ArrayList<>(p));	//一定要写new ArraysList<>(p),写了一定对，不写一定错。
            return;
        }
        for(int i=0;i<nums.length;i++){
            if(st[i]==false){
            	 //和前一个数相同但前一个数还没有用过
                 //比如最开始选择的时候，可以选1,1,2，但是选择第二个1的情况时第一个1还没有用过，所以会跳过这种情况，去重
                if(i>0&&nums[i-1]==nums[i]&&st[i-1]==false)continue;
                path[u]=nums[i];
                st[i]=true;
                dfs(nums,u+1,path,st);
                st[i]=false;
                path[u]=0;
            }
        }
    }
}

2021年8月25日21:36:06：

//这个题目和上面题目的区别在于这个题目中包含重复数字，比如[1,1,2]只有三个全排列，而如果没有重复数字则3个元素应该是有3!=6个全排列
//爆搜，我们枚举每一个位置上可以填哪些数，那么我们如何该避免重复枚举呐？我们仿照三数之和,四数之和的题目:我们对数组进行从小到大排序，这样相同数都跑到了一起
//避免重复枚举：对于相同数，我们只使用第一个，即当nums[i-1]==nums[i]&&st[i-1]==false的时候，我们就跳过，即当前数和前一个相同，
//并且前一个相同的数还没有被用过，那我们就不能使用当前数，如果不满足两个条件的话，就说明是第一个还没有别用过的数，我们就使用这个数
//类似于“嫡长子继承制”，只要老大还活着(即还没有被用过)，我们就不能使用老二，
class Solution {
    List<List<Integer>> res=new ArrayList<>();
    List<Integer> path=new ArrayList<>();
    boolean[] st; //判重数组
    public List<List<Integer>> permuteUnique(int[] nums) {
        Arrays.sort(nums);  //注意注意注意先将数组进行排序，否则下面的操作将是无用功
        int n=nums.length;
        st=new boolean[n];
        dfs(nums,0);  //从下标0开始递归填数
        return res; //递归结束，返回答案
    }
    public void dfs(int[] nums,int u){
        if(u==nums.length){ //枚举完了数组中的所有数字
            res.add(new ArrayList<>(path)); //就把当前路径加到答案中
            return; //递归结束语句，return;不可不写
        }
        for(int i=0;i<nums.length;i++){ //否则我们就枚举一下nums数组中的每一个位置上的数字是否被填过
            if(st[i]==false){ //st[i]==false,即nums数组中的第i位上的数字还没有被用过，我们才考虑将这个nums数组中的nums[i]填到path的第u位上
            //否则的话，即st[i]=true,当前nums数组的这一位已经被用过了，那么我们就不需要再考虑这一位了，即这里的if不用写else语句
                if(i>0&&nums[i-1]==nums[i]&&st[i-1]==false) continue; //对于相同数，我们只使用第一个，当当前数和前一个相同，并且前一个数还没有被用，我们就先跳过这个数，继续判断下一位数
                //否则我们就可以使用当前数，下面的操作和上一题的一样，同时记得要做回溯操作
                st[i]=true;
                path.add(u,nums[i]);
                dfs(nums,u+1);
                //回溯
                st[i]=false;
                path.remove(u); //这一步的回溯操作可写可不写
            }
        }
    }
}

2021年10月23日14:45:52：

class Solution {

//这个题目是包含重复数字的全排列问题,还是枚举每一个位置填哪个数(可以保证字典序),比如第一个位置上填1行不行,填1之后再把所有第一个位置上填1的方案都找出来
//但是这样并没有保证不枚举重复的方案,比如对于[1,1,2],第一个位置上我们可以填第一个1,第一个位置上我们也可以填第二个1,
//但是其实第一个位置上不管填的第一个1还是填的第二个1,结果都是一样的(即是同一个排列),我们要想一个措施来保证不枚举重复的方案,
//出现重复的原因是我们考虑将这两个1视为了不同的1(因为排列问题即可以从前往后看,也可以从后往前看),但是其实这两个1是同样的1,
//所以我们就需要保证相同的数字的相对位置不发生改变,即我们规定对于1,1',1",...我们规定它们的相对位置是1必须要在1'的前面,1'必须要在1"的前面,...
//即我们要规定相同数的相对位置不发生改变,即1 _ _ _ 1' _ _ 1"_ _ _ _...,在写代码的时候,即是对于相同的数,我们只用第一个没有被用过的,
//比如有1,1',1",1''',1"",1""',这样相同的5个1,当我们该填第k个位置上的数了,如果第一,二,三个1已经被用过了,现在我们还想用1的话,那我们就不能使用第五个1,而必须先使用第4个1
//这样我们就可以保证相同数的相对位置不发生改变了,为了让相同数都放在一起,我们可以先对数组排个序,这样相同数都会在一起了,
//这样之后我们在枚举使用每一个数的时候,只使用第一个没有被用过的(用过的就用过了不用管),也就是如果这个数不是第一个没有被用过的我们就把它pass掉,
//还是上面的5个1的例子,如果我们现在枚举的是第五个1,而第四个现在还没有被用过,那我们就先pass掉这种情况,
//所以这里我们和上一个题目一样同样需要一个布尔数组st[i]来表示nums数组的第i个下标上的这个数是否被用过了,
//具体在判断的时候,我们先对数组排个序,之后枚举path数组第u个位置上填哪个数的时候,如果nums[i]==nums[i-1],
//并且nums[i-1]还没有被用过(即st[i-1]==false),那我们就跳过nums[i],即满足nums[i]==nums[i-1]&&!st[i-1],那我们就跳过继续看下一个位置(i+1)上的数,
//其他的代码和上一个题目基本上完全相同,不同点就是要对数组排序,并且不需要统计数字的个数,因为排列问题是强调顺序的,即只要顺序不同即视为不同的方案

    List<List<Integer>> res=new ArrayList<>();
    List<Integer> path=new ArrayList<>();
    boolean[] st;   //状态数组st[i]表示nums数组的第i个位置上的数是否被用过了,st[i]为false表示没有被用过,为true表示已经被用过了
    //注意st[i]==false才表示nums数组的第i个位置上的数没有被用过,st[i]=true代表nums数组的第i个位置上的数被用过了
    int[] num;  //为了少传递一个参数,将nums数组定义为全局的
    int n;  //n是nums数组的长度
    public List<List<Integer>> permuteUnique(int[] nums) {
        Arrays.sort(nums);  //先对数组排序,排序是之后一切操作的基础,没有排序后序的所有操作都免谈
        num=nums;
        n=num.length;
        st=new boolean[n];  //初始化st数组的长度,默认都是false,即都没有被用过
        dfs(0); //0是代表我们现在该填的是path数组的第几个位置了,从第0个位置开始填数字,注意不是现在枚举到了nums数组的哪一个位置了
        //枚举nums数组的操作是放到了dfs函数中了
        return res; //递归结束返回答案数组res
    }
    public void dfs(int u){ //在dfs的过程中完成所有排列的选取,u是当前该填path数组的哪一个位置了,u是枚举的是path数组的位置,不是该填nums数组的哪一个数了
        if(u==n){ //如果已经填完了path数组的所有位置,就说明我们找到了一组解(即一个nums数组的排列),我们就把path加到res中
            res.add(new ArrayList<>(path));
            return;
        }
        //否则就说明path数组还没有填够,我们就来枚举一下nums数组,来看一下当前u位置上可以填哪些数字
        for(int i=0;i<n;i++){ //这里枚举的是当前path数组的u位置上我们可以填nums数组的哪些数字
            if(st[i]==false){  //首先下面所有判断即其他的操作的前提都是当前数没有被用过(st[i]==false),当前数被用过的话,我们就不用管这种情况了,
                if(i>0&&num[i]==num[i-1]&&!st[i-1]) continue;  //如果当前数和nums数组的前一个数相同,并且前一个数还没有被用过,
                //即当前数不是第一个没有被用过的相同的这一段的第一个数,我们就跳过这种情况,嫡长子继承制,和上一题不一样的地方就是多了排序加这一行代码
                //当前数我们就不能用,应该pass掉,即continue,这里因为要有前一个数所以也要保证i>0(i=0的话是nums数组的第一个数是没有前一个数的)
                
                //否则path数组的第u个位置上就可以填写当前数num[i]
                path.add(num[i]); //当前数没有被用过并且当前数可以被用,我们就使用当前数,即把当前数加到path中
                st[i]=true; //并把nums数组的第i个位置标记为true,表示nums数组的第i个位置上的数nums[i]已经被用过了,之后就不能再用了
                dfs(u+1); //继续往下递归枚举填写下一个位置上可以填什么数
                //递归结束的时候需要恢复现场,即回溯操作
                st[i]=false;  //恢复现场,即将nums数组的第i个位置上的状态标记为未使用,即st[i]=false,并去除刚添加的数
                path.remove(path.size()-1);
            }
        }
    }
}

51. N 皇后

51题是求具体不同的方案，而52题是求方案数量。

n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

给你一个整数 n ，返回所有不同的 n 皇后问题 的解决方案。

每一种解法包含一个不同的 n 皇后问题 的棋子放置方案，该方案中 'Q' 和 '.' 分别代表了皇后和空位。

示例 1：

输入：n = 4
输出：[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
解释：如上图所示，4 皇后问题存在两个不同的解法。

示例 2：

输入：n = 1
输出：[["Q"]]

提示：

• 1 <= n <= 9
• 皇后彼此不能相互攻击，也就是说：任何两个皇后都不能处于同一条横行、纵行或斜线上。

算法分析
(DFS暴力搜索) O(n!)
遍历每一行，并记录哪些列、哪些对角线已经被占据；
能填完n行的，就记录一下答案。

时间复杂度
只考虑列的互相约束，时间复杂度上界为n!，实际运算还会考虑对角线约束，复杂度会更低。
空间复杂度 O(n²)

接图：比如图中红圈里对角线k=y-x+n=1-1+2=2,即在第二条对角线上，反对角线k=y+x=1+1=2,在第二条反对角线上。
y总代码和图片的行列有点不照应。
图中x，我们在代码中是i, 即列，
图中y，我们在代码中是u, 即行，

算法分析

dfs

按行继续比遍历，其中col[x],dg[y - x + n],udg[x + y]分别记录的是该位置的列，斜，反斜线上是否已经存在过，若均不存在，填入皇后，并递归到下一行

代码：

class Solution {
public:
    vector<vector<string>> ans; //记录答案
    vector<string> path;    //记录当前搜索的方案
    vector<bool> col;   //列数组，均初始化为false,代表本列，本对角线，本反对角线均没有填过元素，填写元素，就更新为true。
    vector<bool> dg;    //正对角线
    vector<bool> udg;   //反对角线
    vector<vector<string>> solveNQueens(int n) {
        col=vector<bool>(n，false);
        dg=udg=vector<bool>(2*n,false);
        // 初始化棋盘，也可以用两层for循环的方式
        path=vector<string>(n,string(n,'.'));   //初始化棋盘，均为'.'，即一开始均为空，注意初始化方式。// 初始化为n个点.
        // 按照行进行搜索
        dfs(n,0);   //从第0行开始搜，
        return ans; //搜完之后返回答案
    }
    // DFS递归遍历
    void dfs(int n,int u){  //u是当前行数（0~n-1）
        if(u==n){   //如果枚举完了最后一行u等于了n，说明我们找到了一组答案，
            ans.push_back(path);    //往答案中加入这个解，
            return;
        }
         // y = x + k; 截距k = y - x + n (由于可能小于0所以加n变为正)) 
        // y = -x + k; k = y + x;
        //否则的话，我们就要正常递归
        for(int i=0;i<n;i++){   //搜索每一列i
        	// 确保当前单元可以放皇后
            if(col[i]==false&&dg[u-i+n]==false&&udg[u+i]==false) {  //如果当前列，当前正对角线，反对角线均没有被搜索过，说明当前行u，当前列i可以填皇后‘Q’,
                path[u][i]='Q'; //在位置（u,i）填写皇后
                col[i]=dg[u-i+n]=udg[u+i]=true; //更新，将当前列，当前正对角线，反对角线标记为已填写皇后
                dfs(n,u+1); //接着往下一行摆放皇后
                // 恢复现场
                path[u][i]='.'; //恢复现场，将当前位置恢复为空格
                col[i]=dg[u-i+n]=udg[u+i]=false; //更新，将当前列，当前正对角线，反对角线标记为未填写皇后
            }
        }
    }
};

java代码：

class Solution {
    List<List<String>> res=new ArrayList<>();
    char[][] path;
    boolean[] col,dg,udg;
    public List<List<String>> solveNQueens(int n) {
        col=new boolean[n];
        dg=new boolean[2*n];
        udg=new boolean[2*n];
        path=new char[n][n];
        for(int i=0;i<n;i++){
            for(int j=0;j<n;j++){
                path[i][j]='.';
            }
        }
        
        dfs(n,0);
        return res;
    }
    public void dfs(int n,int u){
        if(u==n){
            List<String> list = new ArrayList<>();
            for (int i = 0; i < n; i++) {
                list.add(new String(path[i]));
            }
            res.add(list);
            return;
        }
        for(int i=0;i<n;i++){
            if(!col[i]&&!dg[u-i+n]&&!udg[u+i]) {
                path[u][i]='Q';
                col[i]=dg[u-i+n]=udg[u+i]=true;
                dfs(n,u+1);
                col[i]=dg[u-i+n]=udg[u+i]=false;
                path[u][i]='.';
            }
        }
    }
}

2021年9月17日20:24:56：

//n皇后I是让我们返回具体的解决方案，II是让我们求方案的数量
class Solution {
    int n; //把n记为全局变量
    boolean[] col,dg,udg; //布尔数组col记录这一列是否填过皇后，dg和udg分别记录对角线和反对角线上是否填过元素
    List<List<String>> res=new ArrayList<>(); //记录答案
    char[][] board; //记录当前放置的方案，因为我们来回修改数组，所以这里我们使用字符串数组的形式记录当前棋盘
    public List<List<String>> solveNQueens(int _n) {
        n=_n;
        col=new boolean[n]; //列有n列
        dg=new boolean[2*n]; //对角线有2n-1条
        udg=new boolean[2*n]; //反对角线有2n-1条
        board=new char[n][n]; //初始化board数组的大小是nXn
        //我们需要先将棋盘初始化为空即'.'
        for(char[] c:board){
            Arrays.fill(c,'.'); //先将数组中的所有数初始化为'.'
        }
        dfs(0); //我们来爆搜一下，从第0行开始搜，注意我们这里是一行一行搜的，
        return res; //爆搜结束返回答案
    }
    public void dfs(int u){ //u是当前要放第几行的皇后，即搜索到第几行了
        if(u==n){ //如果u等于了n,上面我们已经搜完了最后一行，已经到达了最后一行的下一行，就说明我们找到了一组方案
            List<String> t=new ArrayList<>();
            for(int i=0;i<n;i++){
                String s="";
                for(char c:board[i]) s+=c;
                t.add(s);
            }
            res.add(t);
        }
        for(int i=0;i<n;i++){ //否则我们就来枚举一下第u行可以放到哪一个位置，所以i从0到n进行循环判断
            if(!col[i]&&!dg[i-u+n]&&!udg[i+u]){ //当前列，对角线和反对角线都没有被填过皇后，说明当前位置可以填皇后，我们就在当前位置填皇后
                col[i]=dg[i-u+n]=udg[u+i]=true; //将当前位置对应的的列，对角线，反对角线数组设置为true,表示当前位置已经填过皇后
                board[u][i]='Q'; //当前位置上填上皇后
                dfs(u+1); //继续填下一行
                //恢复现场
                board[u][i]='.';
                col[i]=dg[i-u+n]=udg[u+i]=false;
            }
        }
    }
}

52. N 皇后 II

n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

给你一个整数 n ，返回所有不同的 n 皇后问题 的解决方案的数量。

每一种解法包含一个不同的 n 皇后问题 的棋子放置方案，该方案中 'Q' 和 '.' 分别代表了皇后和空位。

示例 1：

输入：n = 4
输出：2
解释：如上图所示，4 皇后问题存在两个不同的解法。

示例 2：

输入：n = 1
输出：1
 

提示：

• 1 <= n <= 9
• 皇后彼此不能相互攻击，也就是说：任何两个皇后都不能处于同一条横行、纵行或斜线上。

代码：

//这一题和上一题基本上完全一样。由于不用记录方案，所以这里我们不用开path数组了。
class Solution {
public:
    vector<bool> col,dg,udg;
    int res=0;  //res记录答案
    int totalNQueens(int n) {
        col= vector<bool>(n);
        dg=udg=vector<bool>(2*n);
        dfs(n,0);
        return res; //将答案返回
    }
    void dfs(int n,int u){	//n是传递值，是n皇后的n,u是当前到第u行了
        if(u==n) {
            res++;  //每找到一组答案让res加一
            return;
        }
        //下面和上一题一模一样
        for(int i=0;i<n;i++){
            if(!col[i]&&!dg[u-i+n]&&!udg[u+i]){
                col[i]=dg[u-i+n]=udg[u+i]=true;
                dfs(n,u+1); //往下一行继续递归，所以这里是u+1,
                col[i]=dg[u-i+n]=udg[u+i]=false;
            }
        }
    }
};

java代码：

class Solution {
    boolean[] col,dg,udg;
    int res=0;
    public int totalNQueens(int n) {
        col=new boolean[n];
        dg=new boolean[2*n];
        udg=new boolean[2*n];	//注意java中这里一定要把dg数组和udg数组分开写
        dfs(n,0);
        return res;
    }
    public void dfs(int n,int u){
        if(n==u){
            res++;
            return ;
        }
        for(int i=0;i<n;i++){
            if(col[i]==false&&dg[u-i+n]==false&&udg[u+i]==false){
                col[i]=dg[u-i+n]=udg[u+i]=true;
                dfs(n,u+1);
                col[i]=dg[u-i+n]=udg[u+i]=false;
            }
        }
    }
}

2021年9月17日21:16:40：

//将上一个题目的代码可以完全不变的放到这个题目，只需要最后返回res.size()即可，这个题目也可以写的简洁一点，即不记录方案了，直接求解方案数，
class Solution {
    int n;
    //不需要再记录每一个方案具体是什么了，也就是说List列表不用开了，但是判重数组还是要开的
    boolean[] col,dg,udg;
    public int totalNQueens(int _n) {
        n=_n;
        col=new boolean[n];
        dg=new boolean[2*n];  //注意在java中不允许用=号连续对变量进行初始化
        udg=new boolean[2*n];
        return dfs(0);  //我们直接在dfs函数中返回方案数即可
    }
    public int dfs(int u){  //dfs函数返回方案数
        if(u==n) return 1;  //如果我们已经搜完了一个方案的话，表示我们找到了一个解，返回1
        //否则就看填在第u行的哪一列
        int res=0;  //res记录方案数
        for(int i=0;i<n;i++){ //列数可以是0~n-1
            if(!col[i]&&!dg[u-i+n]&&!udg[u+i]){ //说明这个位置上可以填
                col[i]=dg[u-i+n]=udg[u+i]=true;
                res+=dfs(u+1);  //往下一行递归求取方案数
                col[i]=dg[u-i+n]=udg[u+i]=false; //恢复现场
            }
        } 
        return res; //最后将答案返回   
    }
}

60. 排列序列（数学）

给出集合 [1,2,3,...,n]，其所有元素共有 n! 种排列。

按大小顺序列出所有排列情况，并一一标记，当 n = 3 时, 所有排列如下：

"123"
"132"
"213"
"231"
"312"
"321"

给定 n 和 k，返回第 k 个排列。

示例 1：

输入：n = 3, k = 3
输出："213"

示例 2：

输入：n = 4, k = 9
输出："2314"

示例 3：

输入：n = 3, k = 1
输出："123"

提示：

1 <= n <= 9
1 <= k <= n!

算法一：（内置next_permutation函数）

class Solution {
public:
    string getPermutation(int n, int k) {
        string res;
        for(int i=1;i<=n;i++) res+=to_string(i);
        for(int i=0;i<k-1;i++){
            next_permutation(res.begin(),res.end());
        }
        return res;
    }
};

算法二：（计数）

按照题目要求分析，如果这个数字的某位排列是确定的，那么接下来的选择是n-1！种方案， 所以这里的选择就是如果确定看它的阶乘数是不是大于k，如果小于k，说明不会是这个数字，如果大于k的话， 那么就在保存当前位的数字，这里还需要一个bool数组保存当前数是不是用过了；

(模拟) O(n2)
举个例子： n=3,k=4
在xxxx中寻找第4个排列；
第一个数字为1到3的xxx各有2!个，所以第一个数字为2;
接下来在2xx中寻找第4−2∗1=2个排列；
第二个数字为1或者3的2xx各有1!个(2已经用过了，不能用了)，所以第二个数字为3;
接下来在23x中寻找第4−2∗1−1∗1=1个排列；
第三个数字为1的23x仅剩1个(2、3已经用过了，不能用了)，所以第三个数字为1。、

代码：

class Solution {
public:
    string getPermutation(int n, int k) {
        string res; //定义答案，题目要求我们返回字符串，所以这里我们定义为字符串
        // 记录使用过的数字,最多到9，但是数组下标是从0开始的，所以这里把st数组开到10，
        vector<bool> st(10,false); //数组st记录当前哪些数被用过了，初始化都没有被用过。
        //遍历每一位
        for(int i=0;i<n;i++){   //i是要填写的字符串的下标，从第0位一直填写到第n-1位共n位
            //每填一个数，就会剩下n - i - 1个阶乘的情况，所以先求阶乘
            int fac=1;
            // 每次填一个位置，计算填这个数总共有多少种排列情况
            //求出当前位后面的阶乘 也就是有多少种组合
            for(int j=1;j<=n-i-1;j++) fac*=j;   //预处理阶乘，注意从1开始，要不然全部是0了
            //从前往后找没有用过的数，如果找到，先看一下填了这个数，总共的排列情况.
//如果大于K，那么应该填这个数，填完更新K，继续缩小范围，再找下一个数；
//如果小于K，那么不是这个数，需要更新K，然后break掉，回到第一个for循环，尝试填入下一个数。
            // 然后判断当前数字j是不是可以填在这个第i位
            for(int j=1;j<=n;j++){
                if(!st[j]){ //第j个数没有被用过// 如果数字j之前没有出现
                    //判断是第k个数否在这个分支里，fac < k 说明k一定在这个分支的前面
                    if(fac<k) k-=fac; //那么就将k减去fac// fac阶乘是不是小于k，如果小于那么k-=fac
                    else{   //否则的话，已经被减到够了，且第j个数没有被用过
                        // 将该数字加入答案，并标记为使用过了// 否则当前j保存在i位置，然后j对应的bool设置为true，break
                        res+=to_string(j);  //第k个数的第i位应该填j
                        st[j]=true; //将这个数j标记被用过了
                        break;//每一位只能填一个数，所以一定记得要break，不写break,这一位会被其他数覆盖。
                    }
                }
            }
        }
        return res;//返回答案
    }
};

2021年9月1日10:33:11：

要想解决本题，首先需要了解一个简单的结论：

对于 n 个不同的元素（例如数1,2,⋯,n），它们可以组成的排列总数目为 n!

//相当于是模拟的方法,一位一位的模拟填写
class Solution {
    public String getPermutation(int n, int k) {
        StringBuilder res=new StringBuilder(""); //定义答案字符串
        boolean[] st=new boolean[10]; //数组st记录当前哪个数已经被用过了，共1-9是9个数，我们可以开打一些，st默认初始化为false
        for(int i=0;i<n;i++){ //我们从第0位开始看，一直看到第n-1位
            //我们先看一下当前位如果填一个数之后有多少种情况呐，比如说n=4,第一位填写2的话，则共(n-1)!=6种，如果是第2位填写3的话，则共2!=2种。即是每一位是有(n-i-1)!种情况，即(n-i-1)!个数
            int fact=1; //定义当前位上填写数之后的情况个数，因为是用阶乘!算的，所以要定义为1
            for(int j=1;j<=n-i-1;j++) fact*=j; //从1开始循环。计算n-i-1的阶乘
            //下面开始从小到大看一下当前这一位需要填哪一位数或者说哪一个数，当然我们在枚举的时候要看一下哪些数没有被用过，我们要枚举哪些没有被用过的数
            for(int j=1;j<=n;j++){ //从1开始枚举到n，填写每一位，注意每一位只能填写一个数，所以下面的else语句中的break一定不要忘了写
                if(st[j]==false){  //即如果j这个数没有被用过，注意我们让st数组的下标和值相对应
                    if(fact<k) k-=fact; //如果fact<k,上面这个分支是第k个排列的分支，即k个排列是在这个分支的后面,我们现在就减去fact,几把这些较小数减去
                    else{  //否则就说明当前数没有被用过，并且当前这一位就要填写这个数
                        res.append(j+"");  //把当前这个数填写到答案字符串中
                        st[j]=true; //用完j之后，记得将st[j]标记为true，表示这个数已经被用过了，后面就不能再用这个数了
                        break;  //这里特别容易忘，即是说当前这一位已经填写好了，我们就不要再继续往下枚举了，否则再第11行for循环里再次执行else语句的话，res会加上别的话，或者说每一位只能填一个数
                    }
                }
            }
        }
        return res.toString();  //最后将答案StringBuffer转转为String输出
    }
}

77. 组合

给定两个整数 n 和 k，返回 1 ... n 中所有可能的 k 个数的组合。

示例:

输入: n = 4, k = 2
输出:
[
  [2,4],
  [3,4],
  [2,3],
  [1,2],
  [1,3],
  [1,4],
]

好马不吃回头草
算法分析：

枚举每个位置选哪些数，记录start表示从start数开始枚举到n，在u的位置放哪些数，递归到下一层。

组合里面AB和BA是一样的，这时候只要人为规定一下选元素的顺序，即按顺序选，就可以不选出重复方案了。

dfs(n,k,start)

表示：1_{n**一共**n**个数，还需要选**k**个（这样每次选完**把k减1**就行了），从**1}n一共n个数中的start位置开始选（start前面的不能选）。

*时间复杂度 O(Cnk)k
组合类型，直接把答案选出来，从n个数中选k个

dfs(n,k-1,i+1);
题目给定两个整数 n 和 k，返回 1 … n 中所有可能的 k 个数的组合。其实就是求由1 ~ n的数字组成集合的子集，并且子集的个数刚好是k的所有子集方案。因此我们可以在求子集的同时再添加一个参数s,来表示当前该子集中的元素个数，当个数刚好为k时，即可加入方案，具体代码实现如下：

class Solution {
public:
    vector<vector<int>> res;    //记录所有方案
    vector<int> path;   //记录当前路径方案
    vector<vector<int>> combine(int n, int k) {
    	//k表示: 到终点还需要几个数
        dfs(n,k,1); //n是最大值是n,k是共k个数，1是组合从1开始选
        return res; //返回答案
    }
    void dfs(int n,int k,int start){    //组合中最大值为n,k是需要凑k个数，从start数开始选
        if(k==0){
            res.push_back(path);    //如果凑够了k个数，就说明找到了一组方案，加到方案数组中。
            return;
        }
        //否则的话，就需要选择方案上的数了
        for(int i=start;i<=n;i++){  //i从start开始选，最大选到n
            //选当前数
            path.push_back(i);  //注意这里是把i加到当前路径上，不是start
            dfs(n,k-1,i+1); 当前填的是i，下一位最少从i+1开始考虑，并且需要凑的数也要减一(k-1),注意传入的是i+1。
            //回溯
            path.pop_back();    //恢复现场。
        }
    }
};

2021年8月26日10:54:44：

//从n个数里面选k个数，组合类问题最需要考虑的就是判重，比如是：1,2,3，选2个数的话，那么1,2和2,1就是重复的，之所以会重复，是因为选的顺序是不同的，
//那么如果我们人为规定一下选的顺序，这样就可以不枚举重复的方案,比如规定必须从前往后先，比如说我先选了3，后头再选1，这样不行，好马不吃回头草
//我们选1，再选3，不能先选3再选1，这样的话，我们人为规定了选取的顺序就可以避免重复枚举，只要从前往后选就可以保证选取的顺序是唯一的了
//所以我们在外部dfs的时候，需要传递的参数有: 1.从1到n选的那个n，2.当前选了几个数，选了u个数(u<=k), 
//3.由于我们要按照顺序选，所以第三个参数是:当前可以从第几个数start开始选，比如我们现在现在选到5了，当前只能从6开始选，即dfs(n,u,6)
//当然了，上面我们说第二个参数是当前选了几个数，我们也可以是当前还需要选几个数，即当u=0的时候就说明我们此时找到了一条合法路径
//递归的本质是函数的调用，
class Solution {
    List<List<Integer>> res=new ArrayList<>();  //记录答案
    List<Integer> path=new ArrayList<>();  //当前路径
    public List<List<Integer>> combine(int n, int k) {
        dfs(n,k,1); //n可以传入也可以作为全局变量定义在外面，k是当前枚举了几个数，每枚举一个数，k--,当k=0的时候即说明找到了一条合法路径，1是说我们从1开始枚举
        return res; //递归结束，返回答案res
    }
    public void dfs(int n,int k,int start){ //编写外部dfs函数,k是当前还需要枚举几个数，start是当前可以从哪个数字开始选
        //递归结束语句
        if(k==0){ //当k=0的时候，我们就找到了一条合法路径，就把path加到res中，这也是递归结束语句，return;不要忘了写
            res.add(new ArrayList<>(path));
            return;
        }
        //否则就是正常的从前往后遍历，把数据加到res中的过程
        for(int i=start;i<=n;i++){ //从start开始选，最多选到n
        	剪枝优化：
        	 // 优化，从start开始选最多能选n-start+1个数，如果都不足k个，就没法选
            if (n - start + 1 < k)
                break;
            // 选这个数，然后继续往下
            path.add(i);  //当前选的数是i,把i加到path当前路径中
            //把i加到path中之后，继续往下递归
            dfs(n,k-1,i+1); //继续往下递归，当前由于还需要加的数还有k-1个，并且当前只能从i+1继续往后选，注意哈不是start+1，而是i+1,
            //因为我们是在循环中，当i往后多走几步的时候，就不是start+1了，而是i+1,这一点很容易写错，一定要注意
            //并且dfs的返回为空，所以这里不需要写return,即不是return(n,k-1,i+1),而如果是有返回值的dfs，是需要写return的?
            //注意path是共用的一个，所以我们这里需要做回溯操作，并且那里做的操作，我们就在那里做回溯操作
            path.remove(path.size()-1); //回溯现场
        }
    }
}

2021年10月22日21:56:25：

class Solution {

//这个题目不是组合总和题目了,但是还是组合的题目,代码和之前的组合总数的还是很类似,
//这个题目是给我们两个数n,k,让我们返回所有的[1,n]中的所有k个数的组合,比如n=4,k=2,即是从[1,2,3,4]中随意抽2个数
//因为是组合,所以是去重的,为了避免重复,组合类型的选取最重要的是判重,如[1,2]和[2,1]是同一种方案,我们可以人为规定只能从前往后选,好马不吃回头草
//比如当前已经选到5了,则dfs再往下递归的时候下一个数就要从6开始选,这样就可以保证我们选的时候是从前往后选的,
//所以我们需要在dfs的参数中记录一个start,表示当前可以从第几个数可以选,一开始是1表示从1开始选,同样的,这里的k我们使用的是减法
//递归不要想的太难,递归的本质就是函数的调用,
//时间复杂度是k*Cn,k,乘以的k是记录方案的时间

    List<List<Integer>> res=new ArrayList<>();
    List<Integer> path=new ArrayList<>();
    int n;  //n是最大可以选的数,定义为全局的,就可以不用在dfs中传递了

    public List<List<Integer>> combine(int _n, int k) {
        n=_n;
        dfs(1,k);  //从1开始递归,当前还需要找的数的个数是k个
        return res; //递归结束返回res
    }
    public void dfs(int start,int k){ //在dfs的过程中完成所有组合的创建,start是当前从哪一个数可以找,k是还需要找几个数
        if(k==0){   //如果k=0了,就说明我们找够了k个数,即我们找到了一组解,我们将path加到res中
            res.add(new ArrayList<>(path));
            return;
        }
        //否则就说明k个数还没有找够,我们就要从start开始选,直到选够k个数
        for(int i=start;i<=n;i++){  //从start开始选,最大可以选到n
            path.add(i);  //选了i就把i加到path中，这里就没有总和的限制了，所以只要还没有找够k个数，我们就可以直接选当前数i
            dfs(i+1,k-1);   //继续往下递归,因为已经选了一个了,所以k要减一,并且传递的是i+1,不是start+1,
            //回溯,恢复现场
            path.remove(path.size()-1);
        }
    }
}

78. 子集

本题和90.子集II不同的地方是：78题：数组中的元素互不相同。90题：可能会包含重复的元素。
相同的地方：解集中均不能包含重复的子集。

给你一个**整数数组** nums ，数组中的元素 互不相同 。返回该数组所有可能的子集（幂集）。

解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。

示例 1：

输入：nums = [1,2,3]
输出：[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]

示例 2：

输入：nums = [0]
输出：[[],[0]]
 

提示：

1 <= nums.length <= 10
-10 <= nums[i] <= 10
nums 中的所有元素 互不相同

求子集相对于求全排列来说简单不少，因为我们在考虑方案时，对于每一个数，我们只有选或不选两种选择，因此如果像全排列那样画出递归搜索树，求子集的递归搜索树正好是一棵满二叉树。所有方案刚好是所有叶子结点，因此对于一个大小为n的集合来说，所有子集的个数为2ⁿ个。

算法一：dfs + 回溯法

思路：每个数可选可不选。

和全排列的做法一样，当我们走到叶子结点时，就把该路径加入方案中。如果还没有走到叶子节点，那么对于枚举的当前数，我们有两种选择，选或不选，做出选择再递归到下一层，同时记得回溯。

dfs:枚举每个位置的数 选 还是 不选，并递归到下一层，当u == nums.length时，表示有一种满足题意的情况，加入到ans链表中

时间复杂度 O(2ⁿ *n)

典型的dfs的题目，要注意这里要进行回溯，进行dfs判断当前这个元素选还是不选从而形成分支。

举个例子[1,2,3],从根节点出发根节点是个空集，判断1这个元素选或者不选形成分支

接下来到2这个数字重复上个动作选或者不选形成分支。。。

当一个分支走完时，要注意回溯会上次的状态

参考下面图示

dfs代码：

class Solution {
public:
    vector<vector<int>> res;    //记录答案/结果二维数组
    vector<int> path;   //记录每次路径/当前装入的元素
    vector<vector<int>> subsets(vector<int>& nums) {
    	//最先从第0个下标开始dfs
        dfs(nums,0);    //0表示nums数组的下标，我们从0开始。
        return res; //返回答案  
    }
    void dfs(vector<int>& nums,int u){  //u表示nums数组，u一直在往后移动（除了回溯的时候）
        if(u==nums.size()){ //到达最后一个位置
            res.push_back(path);    //找到了一组答案，把当前方案放到答案数组中。
            return;	//这是递归结束条件，这里一定要写return;从而结束递归。不写的话会堆栈溢出错误。
        }
        //不选当前元素，直接进入下一个元素
        dfs(nums,u+1);  //不选当前数，直接递归下一层
        //选择pos位置元素,加入path内
        path.push_back(nums[u]);    //选当前数，把当前数加到答案数组中。
        //选择当前元素后进入，下一个元素
        dfs(nums,u+1);  //再递归下一层
        path.pop_back();    //回溯。很重要。！！！
    }
};

算法二：

用二进制的方法

由于每个数有选和不选两种情况，因此总共有 2^n 种情况，用二进制 0 到 2^n-1 表示所有的情况（如3个数的集合就用000~111表示），在某种情况i中，若该二进制i的第j位是1，则表示第j位这个数选，加入到path中，枚举完i这种情况，将path加入到ans答案数组中。

位运算法
在前面的分析中我们知道对于每个数，我们可以选或者不选，两种选择刚好对应两种状态，因此我们可以采用位运算的思路进行求解。对于一个大小为n的集合来说，我们需要用一个n位二进制数来表示每个数的选择状态，所有方案刚好是所有叶子结点，所有子集的个数为2ⁿ个，所以每个叶子结点的状态刚好可以用0 ~ 2ⁿ−1中的二进制数表示。

例如对于集合：[1, 2, 3]

代码：

class Solution {
public:
    vector<vector<int>> subsets(vector<int>& nums) {
        vector<vector<int>> res;    //记录答案。
        int n=nums.size();  //n记录数组长度。
        for(int i=0;i< 1<<n;i++){   //枚举从0到2^n-1，共2^n个子集，注意这里是1<<n,不是2<<n。// 1 ~ 2^n - 1
            vector<int> path;   //记录这一次的答案,注意path不能作为全局变量了。
            for(int j=0;j<n;j++){   //枚举二进制每一位是0还是1（如图片样例n=3,）// n位二进制的每一位
                if((i>>j)&1){    //看一下i的第j位是0还是1，如果第j为是1的话，我们就把这个数（nums[j]）加到方案数组中，注意这里是（i>>j&1）。
                    path.push_back(nums[j]);
                }
            }
            //每结束一次for循环，我们就得到了一个子集，就把这个子集加到方案里。
            res.push_back(path);
        }
        return res;    //最后记得将答案返回。
    }
};

2021-8-26 11:34:39：

算法1 DFS

枚举每个位置的数 选 还是 不选，并递归到下一层，当u == nums.length时，表示有一种满足题意的情况看，加入到**ans**链表中

时间复杂度 O(2^n)

//方法一：dfs,这个题目是让我们求不包含重复元素的数组的子集，我们使用递归，枚举一下每个数选或者不选来解决
class Solution {
    List<List<Integer>> res=new ArrayList<>();
    List<Integer> path=new ArrayList<>();
    public List<List<Integer>> subsets(int[] nums) {
        dfs(nums,0); //从数组nums的下标0开始枚举 
        return res; //当递归结束返回答案链表数组
    }
    public void dfs(int[] nums,int u){
        if(u==nums.length){ //当枚举完了数组中的所有数，我们就找到了一个子集，加到答案中
            res.add(new ArrayList<>(path));
            return;
        }
        //选当前数，注意这个题目不要写for循环，上个题目之所以要写for循环，是因为数据没有用数组给出，我们要自己一点一点使用for循环把数据枚举出来
        //而这个题目中的数据是用数组给出来的，所以这个题目我们不要写for循环，
        path.add(nums[u]);
        //往下一个数继续递归
        dfs(nums,u+1);
        //回溯
        path.remove(path.size()-1);
        //不选当前数，继续递归判断下一个数
        dfs(nums,u+1);
    }
}

算法二：

子集，实际上就是考虑每个数字是否出现在集合中。一个数出现与不出现共两种情况，因此 n 个数的子集共有 2ⁿ 个。把这 n 个数对应到 n 位二进制上，每个数出现与否体现为二进制位为 0 或 1。因此，在 [0,2ⁿ) 之间的每一个数的二进制信息就能唯一确定一个子集。

比如对于集合 [1,2,3], 001 就表示只取第 1 个元素，构成集合为 {1}。101 就表示只取 1 和 3，表集合 {1,3}。

//方法二：迭代实现，使用二进制，由于每个数有选和不选两种情况，因此总共有 2^n 种情况，用二进制 0 到 2^n-1 表示所有的情况，
//在某种情况i中，若该二进制i的第j位是1，则表示第j位这个数选，加入到path中，枚举完i这种情况，将path加入到ans链表中
//时间复杂度是：O(n*2^n)
class Solution {
    public List<List<Integer>> subsets(int[] nums) {
        List<List<Integer>> res=new ArrayList<>();  //定义答案数组
        int n=nums.length;  //数组的长度
        for(int i=0;i<(1<<n);i++){  //1<<n,1左移n位即2^n,我们也可以写Math.pow(2,n)
            List<Integer> path=new ArrayList<>(); //当前路径是path
            for(int j=0;j<n;j++){ //枚举数字i的每一位
                if(((i>>j) & 1) ==1){ //判断i的第j位上的数字是否是1，如果是1的话，就说明当前位上有这个数，加到path中,&1即是判断i的第j位,
                //注意i的第j位，是i右移>>j位，注意该加的小括号一定不要少加了
                    path.add(nums[j]); //把nums数组中的第j位元素，即nums[j]加到当前路径中             
                }
            }
            res.add(new ArrayList<>(path));  //每枚举完一位这个数字，即是找到了一个子集，就把这个子集加到答案中
        }
        return res; //最后返回答案
    }
}

2021年10月23日12:45:32：

class Solution {

//这个题目是求不包含重复数组nums的所有子集，因为要求出所有具体的方案，所以我们使用dfs来完成即可，枚举nums数组每一个位置上的数选或者不选来记录方案

    List<List<Integer>> res=new ArrayList<>();
    List<Integer> path=new ArrayList<>();
    int[] num;
    int n;
    public List<List<Integer>> subsets(int[] nums) {
        num=nums;
        n=num.length;
        dfs(0); //从nums数组的第0个下标开始递归枚举
        return res; //递归结束返回答案数组
    }
    public void dfs(int u){ //在这里u是枚举的nums数组的下标
        if(u==n){ //找到了一个解
            res.add(new ArrayList<>(path));
            return;
        }
        //首先是不选当前数，即直接往下递归看nums数组的下一个位置上的数，没有选取当前数，所以不需要回溯操作
        dfs(u+1);
        //也可以选择当前数，即把当前数nums[u]加到path中，选取了当前数，下面递归结束返回的时候就需要回溯操作
        path.add(num[u]); //选取当前数
        dfs(u+1); //选完之后继续往下递归即看枚举看nums数组的下一个位置上的数字是否选取
        //选取了当前数，当递归返回的时候就需要回溯操作
        path.remove(path.size()-1);
    }
}

79. 单词搜索

给定一个二维网格和一个单词，找出该单词是否存在于网格中。

单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。

示例:

board =
[
  ['A','B','C','E'],
  ['S','F','C','S'],
  ['A','D','E','E']
]

给定 word = "ABCCED", 返回 true
给定 word = "SEE", 返回 true
给定 word = "ABCB", 返回 false
 

提示：

board 和 word 中只包含大写和小写英文字母。
1 <= board.length <= 200
1 <= board[i].length <= 200
1 <= word.length <= 10^3

算法分析：

DFS

在深度优先搜索中，最重要的就是考虑好搜索顺序。

我们先枚举单词的起点，然后依次枚举单词的每个字母。
过程中需要将已经使用过的字母改成一个特殊字母，以避免重复使用字符。

**时间复杂度分析：**单词起点一共有 n²个，单词的每个字母一共有上下左右四个方向可以选择，但由于不能走回头路，所以除了单词首字母外，仅有三种选择。所以总时间复杂度是 O(n²*3^k)。

空间复杂度分析：递归的空间复杂度取决的最大递归层数，所以这题的空间复杂度是 O(k)，k 是被查找的单词长度。

算法分析
dfs

从单词矩阵中枚举每个单词的起点，从该起点出发往四周dfs搜索目标单词，并记录当前枚举到第几个单词，若当前搜索到的位置(i,j)的元素恰好是word单词第depth个字符，则继续dfs搜索，直到depth到最后一个字符则表示有了符合的方案，返回true

注意：搜索过的位置继续搜索下一层时，需要对当前位置进行标识，表示已经搜索过这个字符，

时间复杂度 O(n * m ) * (3^k)

对于每个起点，k表示搜索的单词的长度，搜索的时候除了来了方向不用搜索，其余3个方向都需要进行搜索，因此3^k种情况，一共有n²个起点，因此时间复杂度是O(n²)*(3^k)

遍历board每个点，看它是否和word开头字母相同，如果相同就就进入dfs过程

dfs(board, word,now, x, y)

board是字母板，word是单词，now是已经匹配了word的位置，x，y是最后一次匹配成功的字母板的位置下标

在dfs过程中 上下左右四个方向去找能匹配word里下个字符的位置

注意： 一定要标记走过的点，避免重复使用 ；dfs递归回溯时，还要把不去走的点标记为可用。

一般搜索需要用 vis 数组记录某个位置是否被访问过，但也可以直接在 board 数组上做标记，可以将某个访问过的点 (x,y) 设置成一个特殊的字符，比如 #。
但是这题可能有多个搜索起点，也就是说，我们在设置完成后还需要恢复其原来的状态（回溯）。

代码：

class Solution {
public:
    bool exist(vector<vector<char>>& board, string word) {
        int n=board.size(); //一共多少行单词
        int m=board[0].size();  //每一行有多少个字符
        //下面就是对每一个字符作为递归起点
        //枚举所有起点
        for(int i=0;i<n;i++){   //
            for(int j=0;j<m;j++){
                if(dfs(board,word,0,i,j)==true) return true;    //每次递归结束，只要找到了要求的单词，就返回true
            }
        }
        return false;   //当所有字符作为起点均不存在要求的单词就返回false。
    }
    int dx[4]={-1,0,1,0},dy[4]={0,1,0,-1};    //定义方向矩阵(偏移量)，分别代表上-0，右-1，下-2，左-3。
    bool dfs(vector<vector<char>>& board,string& word,int u,int x,int y){   //编写递归函数，第一个参数是要被查找的数组（要改变数组中的字符，所以用&），第二个参数是要查找的单词，
        //第三个参数u是查找到了单词的第几个位置，x,y是本次递归查找的起点坐标。
        //易错点：注意2次判断的顺序和第二次判断的条件
        if(board[x][y]!=word[u]) return false;   //如果每次递归的时候不等于word[u]说明这个位置字符不相等，结束本次递归
        if(u==word.size()-1) return true;   //说明此时我们已经搜到了最后一个字符,并且没有执行上面的语句，即说明最后一个字符仍然相等就返回true即可。
        //上面两个if语句没有执行，上面还在查找过程中或者说递归过程中（即board[x][y]==word[u]）
        char t=board[x][y];    //存储下来当前位置是什么，下面回溯还要恢复回来，所以这里我们要先存储下来。
        board[x][y]='.';    //用掉了board[x][y]（因为其和word[u]相同，我们此时已经用掉了board[x][y]）就将其置为一个不存在的字符'.'，表示这个位置已经被用过了，不要重复用。
        for(int i=0;i<4;i++){   //枚举四个方向
            int a=x+dx[i],b=y+dy[i];    //新方向的下标
            if(a<0||a>=board.size()||b<0||b>=board[0].size()||board[a][b]=='.') continue;    //如果出界或者这个下一个位置被用过了，就跳过这个字符，继续看下一个字符是否被用过
            else {  //否则说明下一个位置没有出界且没有被用过，我们就对其继续递归
                if(dfs(board,word,u+1,a,b)) return true;    //如果递归结果为true，则说明下一个位置的字符是匹配的，
            }
        }
        //恢复现场，回溯
        board[x][y]=t;  //恢复现场，执行到这里，说明26行的：if(dfs(board,word,u+1,a,b)) return true; 没有被执行，
        //即下一个位置的字符上下左右递归均是不匹配的，我们就需要更换新的起始位置，一定要将21行：board[x][y]='.';恢复回来
        return false;   //还要返回false。
    }
};

79题二刷：

class Solution {
public:
    int n,m;
    bool exist(vector<vector<char>>& board, string word) {
        n=board.size();m=board[0].size();
        //枚举所有起点
        for(int i=0;i<n;i++){   //将每个点都作为起点递归一下。
            for(int j=0;j<m;j++){
                //将每个点都作为起始顶点搜索一下，只要有一个点作为顶点搜索到答案，就返回true。
                if(dfs(board,word,0,i,j)==true) return true;  //第三个参数u是搜索到所给单词的哪一个下标，如搜索hello,0就是h,我们肯定从所给单词的下标0开始搜索
            }
        }
        return false;   //如果上面for循环全部结束，还没有返回true，说明根本就不存在这个单词，我们返回false即可。
    }
    int dx[4]={-1,0,1,0},dy[4]={0,1,0,-1};  //方向数组，上右下左。
    //编写dfs函数，u是搜索到所给单词的哪个下标了，x，y是所给“矩阵”点的下标
    bool dfs(vector<vector<char>>& board, string word,int u,int x,int y){
        if(board[x][y]!=word[u]) return false;  //如果搜索到矩阵点不等于所给单词对应的字符，我们就返回false，提前结束本次循环，
        if(u==word.size()-1) return true;    //说明此时我们已经搜到了最后一个字符,并且没有执行上面的语句，即说明最后一个字符仍然相等就返回true即可。
        //下面就要正常搜索，且没有执行第17行if(board[x][y]!=word[u]) return false;说明board[x][y]=word[u]，我们就要用掉board[x][y]
        char c=board[x][y]; //先存储下来当前字符，因为后面还要回溯,恢复现场
        board[x][y]='*';    //board[x][y]被用掉，将其标记为一个不存在的字符即可，所以我们就其标记为‘*’,表示该位置已被用掉，后面不能重复使用。
        //下面是往新方向继续dfs
        for(int i=0;i<4;i++){   //board[x][y]已被用过，我们继续往上下左右四个方向继续递归搜索。
            //新方向的坐标
            int a=x+dx[i],b=y+dy[i];    //下一个方向的坐标。
            //看一下新方向是否越界或者已被用过(即判断board[a][b]是否等于‘*’)
            if(a<0||a>=n||b<0||b>=m||board[a][b]=='*') continue; //如果新方向越界或者新方向被用过，我们就跳过，继续看上右下左的新方向
            //到达这里说明新方向没有越界且没有被用过,继续往新方向递归。
            if(dfs(board,word,u+1,a,b)==true)  return true; //dfs全部结束，等于true，我们就返回true
        }
        //如果上面的for循环结束没有返回true，说明(x,y)这个点不行，我们就需要恢复现场,并且返回false，说明这个点不行。
        board[x][y]=c;
        return false;
    }
};

79题多次刷了，一定要会啊
2021年9月1日12:12:52：

//这个题目是让我们判断二维字母阵中是否存在给定的单词，使用爆搜，爆搜的问题一般都不考虑时间复杂度，
//这个题目我们先枚举起点，再枚举每一步的四个方向(每一个是有上下左右四个方向)，相当于是一个递归搜索树，爆搜的时候，我们要保证搜索的时候要不重不漏，
//当选取一个方向走了一格之后比如样例1中的从s走到f之后，就只有三个方向可以走了，之后再选取一个方向走一格之后，之后又只有三个方向可以走,这样就可以搜出来所有方案
//时间复杂度：共n*m个起点，路径长度是k的话，每一步有三种情况，所以时间复杂度就是n*m*3^k
//而搜索四个方向的时候，我们用多次用到的方向数组或者说是方向矩阵，注意回溯操作
class Solution {
    int[] dx={-1,0,1,0},dy={0,1,0,-1}; //方向数组，即上右下左
    public boolean exist(char[][] board, String word) {
        int m=board.length,n=board[0].length;
        for(int i=0;i<m;i++){ //枚举每一个起点，即将每一个节点作为起点，进行dfs爆搜，
            for(int j=0;j<n;j++){
            //这里可以加一句剪枝语句：if(board[i][j]==word[0]),只有这两个相同的时候才继续往下递归，否则就不以这个格子作为起点进行枚举判断
                if(dfs(board,word,0,i,j)==true) return true;  //只有有一个点作为起点爆搜到了答案，我们就提前结束，返回true
                //dfs函数中的第三个参数是当前判断到了要搜索的字符串的第几个下标，刚开始的下标为0，而(i,j)表示当前枚举的字母阵的格子的下标是(i,j)
            }
        }
        return false;  //如果上面的所有点都作为起点之后也没有找到答案，我们就返回false
    }
    //编写外部dfs函数，u是当前判断到了字符串的哪一位即下标，即搜索到了哪一个位置，(x,y)表示当前的格子的下标 ，注意dfs的返回值是布尔boolean
    public boolean dfs(char[][] board,String word,int u,int x,int y){
        if(board[x][y]!=word.charAt(u)) return false;  //如果当前格子的字符不等于我们应该枚举到的字符串的下标对应的字符，我们就返回false
        if(u==word.length()-1) return true; //注意这里我们先判断了board[x][y]是否和word[u]相同，执行到这里说明两者相同。
        //即是说u是字符串的最后一个下标，并且最后一个下标上的字符也相等，我们就返回true
        //否则的话我们就需要搜一下四个方向，并且当前位置board和word[u]字符正好匹配，我们要将其标记为已访问过，否则可能会被再次访问，而每个位置的字符只能用一次
        //我们这里没有开布尔数组，而是采取标记的方法，即是说当前位置上如果被用过了，我们可以将这个位置改为'.',因为'.'不是字母阵的字符
        char t=board[x][y]; //因为我们下面需要回溯操作，当不合适的时候，我们需要将board[x][y]恢复回来
        board[x][y]='.';  //将当前已经用过的数改为'.'，表示之后不能再用当前这个位置上的字符
        //继续往四个方向继续递归判断
        for(int i=0;i<4;i++){ //再往四个方向继续往下递归
            int a=x+dx[i],b=y+dy[i];  //(a,b)是新方向的下标
            if(a<0||a>=board.length||b<0||b>=board[0].length||board[a][b]=='.') continue;  //这里判断是board[a][b],不是board[x][y]
            //如果越界或者当前位置上的字符已经被用过了，我们就跳过这个方向，继续看下一个方向 ,即比如上右下左中的上被用过了，我们就换成右方向
            
            //否则就说明当前位置没有越界并且当前字符没有被用过，我们就继续往下递归判断
            else{
                if(dfs(board,word,u+1,a,b)==true) return true;  //如果当前往下一直递归能找到答案字符串的话，我们就返回true
            }
        }

        //记得恢复现场，在哪里改的就在那里的下面改回来，回溯操作，即将board[x][y]改为原来的字符，我们已经用t存下来了，注意和上面的更改操作的位置要对应
        board[x][y]=t;  //回溯操作，我们就当前格子改回原来的字符t
        return false; //如果上面的for中没有返回true,表示上面以(i,j)为起点的字符中不存在答案路径，我们返回false,及时止损
    }
}

或者这样写：

class Solution {
public:
    bool exist(vector<vector<char>>& board, string word) {
        for (int i = 0; i < board.size(); i ++ )
            for (int j = 0; j < board[0].size(); j ++ )
                if (board[i][j] == word[0])                     //第一个字母相等，开始bfs搜索
                    if (dfs(board, word, i, j, 0)) return true;

        return false;
    }

    bool dfs(vector<vector<char>>& board, string word, int i, int j, int u)
    {
        //在范围外或者当前字母不相符，则返回false
        if (i < 0 || i >= board.size() || j < 0 || j >= board[0].size() || board[i][j] != word[u])
            return false;

        if (u == word.size() - 1) return true;

        board[i][j] = ' ';                                      //置空，防止重复搜索

        int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
        for (int k = 0; k < 4; k ++ )
        {
            int x = i + dx[k], y = j + dy[k];
            if (dfs(board, word, x, y, u + 1)) return true;
        }

        board[i][j] = word[u];                                  //恢复现场

        return false;
    }
};

87. 扰乱字符串

给定一个字符串 s1，我们可以把它递归地分割成两个非空子字符串，从而将其表示为二叉树。

下图是字符串 s1 = "great" 的一种可能的表示形式。

    great
   /    \
  gr    eat
 / \    /  \
g   r  e   at
           / \
          a   t

在扰乱这个字符串的过程中，我们可以挑选任何一个非叶节点，然后交换它的两个子节点。

例如，如果我们挑选非叶节点 "gr" ，交换它的两个子节点，将会产生扰乱字符串 "rgeat" 。

  rgeat
   /    \
  rg    eat
 / \    /  \
r   g  e   at
           / \
          a   t

我们将 `"rgeat”` 称作 `"great"` 的一个扰乱字符串。

同样地，如果我们继续交换节点 "eat" 和 "at" 的子节点，将会产生另一个新的扰乱字符串 "rgtae" 。

    rgtae
   /    \
  rg    tae
 / \    /  \
r   g  ta  e
       / \
      t   a

我们将 "rgtae” 称作 "great" 的一个扰乱字符串。

给出两个长度相等的字符串 s1 和 s2，判断 s2 是否是 s1 的扰乱字符串。

示例 1:

输入: s1 = "great", s2 = "rgeat"
输出: true

示例 2:

输入: s1 = "abcde", s2 = "caebd"
输出: false

首先判断两个字符串的字符集合是否相同，如果不同，则两个字符串一定不可以相互转化。
然后枚举第一个字符串左半部分的长度，分别递归判断两种可能的情况：

• 该节点不发生翻转，则分别判断两个字符串的左右两部分是否分别可以相互转化；

• 该节点发生翻转，则分别判断第一个字符串的左边是否可以和第二个字符串的右边相互转化，且第一个字符串的右边可以和第二个字符串的左边相互转化；

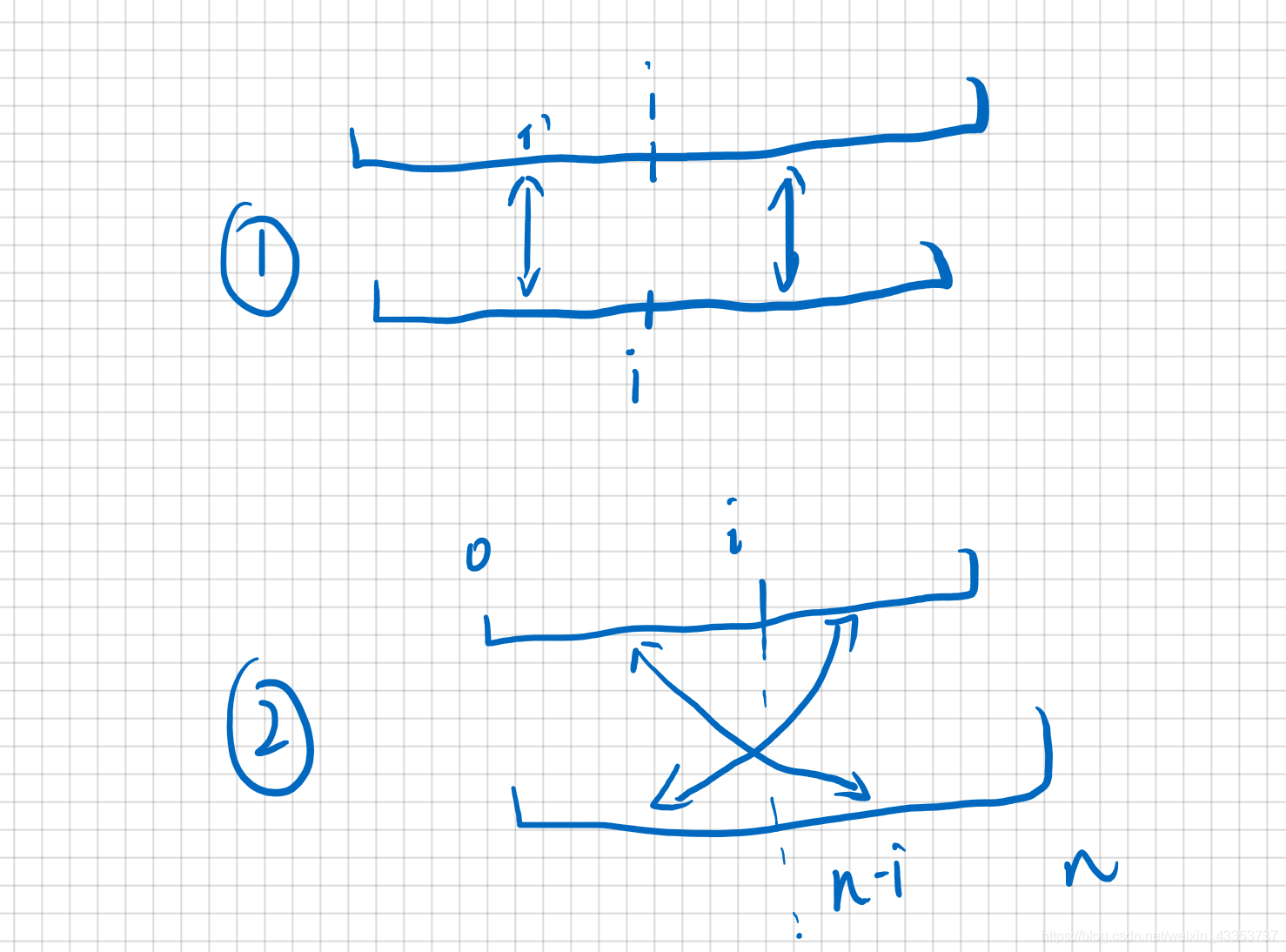
(暴力搜索) O(5^n)
递归判断两个字符串是否可以相互转化。

首先判断两个字符串的字符集合是否相同，如果不同，则两个字符串一定不可以相互转化。
然后枚举第一个字符串左半部分的长度，分别递归判断两种可能的情况：

该节点不发生翻转，则分别判断两个字符串的左右两部分是否分别可以相互转化；

该节点发生翻转，则分别判断第一个字符串的左边是否可以和第二个字符串的右边相互转化，且第一个字符串的右边可以和第二个字符串的左边相互转化；

代码：

class Solution {
public:
    bool isScramble(string s1, string s2) {
        int n=s1.size();
        if(s1==s2) return true; //递归过程中，如果两个字符串相等，就返回true
        string bfs1=s1,bfs2=s2; //做一下备份(bf)，下面要剪枝了
        sort(bfs1.begin(),bfs1.end());  //先排序，方便对字符串进行比较。
        sort(bfs2.begin(),bfs2.end());  //先排序，方便对字符串进行比较。
        if(bfs1!=bfs2) return false;    //如果排完序两个字符串不相等，直接结束本次递归。
        for(int i=1;i<=n-1;i++){    //枚举翻转位置(注意从1开始,因为下面用到了i截取长度，截取长度为0无意义)
            //  不翻转的情况  
            if(isScramble(s1.substr(0,i),s2.substr(0,i))   //递归判断，如果s1的前i个字符和s2的前i个字符可以匹配 
            &&isScramble(s1.substr(i),s2.substr(i))) return true;   //并且两者的后n-i个字符也匹配，说明可以不翻转得到返回true。(substr(i),表示从i截取到最后)
            //  翻转的情况
            if(isScramble(s1.substr(0,i),s2.substr(n-i))   //递归判断，如果s1的前i个字符和s2的后n-i个字符可以匹配 
            &&isScramble(s1.substr(i),s2.substr(0,n-i))) return true;   //并且如果s1的后i个字符和s2的前n-i个字符可以匹配，说明可以翻转得到返回true。(substr(n-i),表示从i截取到最后)
        }
        return false;   //如果上面没有返回true，说明以i作为分隔点不可以，返回false
    }
};

89. 格雷编码

格雷编码是一个二进制数字系统，在该系统中，两个连续的数值仅有一个位数的差异。

给定一个代表编码总位数的非负整数 n，打印其格雷编码序列。即使有多个不同答案，你也只需要返回其中一种。

格雷编码序列必须以 0 开头。

示例 1:

输入: 2
输出: [0,1,3,2]
解释:
00 - 0
01 - 1
11 - 3
10 - 2

对于给定的 n，其格雷编码序列并不唯一。
例如，[0,2,3,1] 也是一个有效的格雷编码序列。

00 - 0
10 - 2
11 - 3
01 - 1

示例 2:

输入: 0
输出: [0]
解释: 我们定义格雷编码序列必须以 0 开头。
     给定编码总位数为 n 的格雷编码序列，其长度为 2n。当 n = 0 时，长度为 20 = 1。
     因此，当 n = 0 时，其格雷编码序列为 [0]。

算法分析
格雷码 构造

算法分析：构造

规律：在上一个结果的基础上进行上下翻转，然后上半部分补0，下半部分补1

操作：补0（左移一位）等价于在原来数的基础上 乘上2，翻转后补1,等价于翻转后的数的基础上 乘上2加1

时间复杂度 O(2ⁿ)

(迭代递归)
代码：

class Solution {
public:
    vector<int> grayCode(int n) {
    	// n = 0时就是一个0
        vector<int> res(1,0);   //将res初始化为长度为1，并且元素为0
        //n!=0
        while(n--){ //执行n次
            for(int i=res.size()-1;i>=0;i--){   //倒序
                res[i]*=2;  //先乘以2，即先左移一位（对称轴上面的也要左移一位）
                //后半部分的每个数补1,并且逆序加入res
                res.push_back(res[i]+1);    //添加新元素：值是乘以2加一之后的值
            }
        }
        return res; //返回答案数组。
    }
};

java代码：

class Solution {
    public List<Integer> grayCode(int n) {
        List<Integer> res=new ArrayList<>();
        res.add(0);
        while((n--)!=0){
            for(int i=res.size()-1;i>=0;i--){
                res.set(i,res.get(i)*2);
                res.add(res.get(i)+1);
            }
        }
        return res;
    }
}

2021年9月1日16:50:02：
镜面反射法

规律：在上一个结果的基础上进行上下翻转，然后上半部分补0，下半部分补1

操作：补0等价于在原来数的基础上 乘上2，翻转后补1,等价于翻转后的数的基础上 乘上2加1

时间复杂度 O(2^n)

注意n=1的时候也符合上面的规律：

//规律：在上一个结果的基础上进行上下翻转，然后上半部分补0，下半部分补1
//操作：补0等价于在原来数的基础上 乘上2(或者是左移一位)，翻转后补1,等价于翻转后的数的基础上 乘上2加1(左移一位之后再加一)
class Solution {
    public List<Integer> grayCode(int n) {
        List<Integer> res=new ArrayList<>();  //先定义答案
        res.add(0); //先将0加到答案中
        while(n--!=0){ //我们需要进行n次操作
            for(int i=res.size()-1;i>=0;i--){ //我们这里是倒着来做的，即是说从对称轴最下面的数开始往上
                res.set(i,res.get(i)*2);  //先将这个数设置为原来的2倍
                res.add(res.get(i)+1);  //随后在res的后面添加这个数的2倍加一的数，注意上面一行已经将这个数变为原来的2倍了，所以我们只需要拿到这个数加一即可
            }
        }
        return res; //最后将答案数组进行返回即可
    }
}

90. 子集 II

本题和78.子集I不同的地方是：78题：数组中的元素互不相同。90题：可能会包含重复的元素。
相同的地方：解集中均不能包含重复的子集。

给定一个可能包含重复元素的整数数组 nums，返回该数组所有可能的子集（幂集）。

说明：解集不能包含重复的子集。

示例:

输入: [1,2,2]
输出:
[
  [2],
  [1],
  [1,2,2],
  [2,2],
  [1,2],
  []
]

算法分析：

算法思路
在LeetCode 78. 子集 中我们知道求子集问题与求全排列问题 的区别在于我们不需要考虑每个数在的位置或每个位置上是什么数，我们只在乎每一个数选或不选。因此对于有重复元素的子集问题，我们的思路不再像全排列那样关心每个数的先后关系，我们只需要关心相同的数选几个。具体步骤如下：

1. 将原数组排序，目的是将相同元素放在一起，之后好计算每个相同数的个数
2. 计算出当前数相同的个数，然后分别做出不选，选1个，选2个…的选择，然后递归到下一层
3. 注意在每做完一个选择递归到下一层时不需要马上回溯，因为我们选1个，选2个…每一个之后的选择是建立在之前选择上多选一个，所以我们不需要马上回溯
4. 当做出所有选择后，我们才需要将选择的这一段相同的数清空，所以回溯需要在做完所有选择后再进行

//这个题目和78题不同，这个题目含有相同元素，78题每个数只能枚举0次或者1次，所以78题可以使用二进制的方法，但是这个题目中含有相同元素，每个数的枚举次数就不止0次或者1次了，可能有多次，所以就不能再使用二进制的方法了。

这个题目的做法或者说思路和第40题. 组合总和 II 基本上完全相同。

代码：

class Solution {
public:
    vector<vector<int>> ans;    //定义答案数组
    vector<int> path;   //用path记录当前方案
    vector<vector<int>> subsetsWithDup(vector<int>& nums) {
        sort(nums.begin(),nums.end());  //先对数组进行排序
        dfs(nums,0);    //从第0个数开始递归枚举
        return ans;     //枚举完之后返回答案
    }
    void dfs(vector<int>& nums,int u){  //编写递归函数，u是数组的下标位置
    	//看21行代码就知道为什么这里要写u==nums.size()了。
        if(u==nums.size()){   //如果u已经枚举完了最后一个数，说明我们已经找到了一种方案，就将这种方案加入到答案数组中
            ans.push_back(path);    //将这种方案加入到答案数组中
            return;    //结束本次递归
        }
        //下面我们来数一下当前这个数的总个数
        int k=u+1;  //从当前数的下一个数开始看
        while(k<nums.size()&&nums[k]==nums[u]) k++;    //数一下当前数一共多少个，最后k落在了最后一个等于当前数的下一个位置
        int cnt=k-u;    //当前数的个数为cnt
        for(int i=0;i<=cnt;i++){    //枚举当前数的出现次数，最少0次，最多cnt次
            dfs(nums,k);    //开始递归枚举下一个数
            path.push_back(nums[u]);    //每次递归就在答案数组中加一个当前数
        }
        //恢复现场，每次递归就将当前加入的当前数清空
        for(int i=0;i<=cnt;i++){
            path.pop_back();
        }
        //返回值为空，这里不需要返回语句。
    }
};

疑惑点：为什么DFS在path.push_back()之前？
答：这样可以枚举出选0个、1个、… k - u个当前数的情况。
或者也可以把选0个单独处理，dfs就在path.push_back()之后了

即：

int k = u + 1;
    while(k < nums.size() && nums[k] == nums[u])  k ++;
    // 当前枚举的数有 k - u 个，枚举其选多少次 0~ k - u次
    dfs(nums, k) ; // 一个都不选
    for(int i = 1; i <= k - u; i ++) // 枚举选的次数
    {
        path.push_back(nums[u]);
        dfs(nums, k);
    }

     for (int i = 1; i <= k - u; i ++ ) 
        path.pop_back();   

二刷90题：

class Solution {
public:
    vector<vector<int>> res;    //记录答案 
    vector<int> path;   //path记录当前方案
    vector<vector<int>> subsetsWithDup(vector<int>& nums) {
        sort(nums.begin(),nums.end());  //先对数组进行排序，之后可以方便的计数数组中相同元素的个数
        dfs(nums,0);    //从第0段开始枚举
        return res; //将答案返回
    }
    void dfs(vector<int>& nums,int u){  //u是枚举到数组的当前段
        if(u==nums.size()){ //枚举完全段，说明我们找到了一组答案。
            res.push_back(path);
            return;
        }
        //否则我们就需要找一下当前段中数的个数
        int k=u+1;
        while(k<nums.size()&&nums[k]==nums[u])k++;  //k最后到达新端
        int cnt=k-u;    //当前段的个数
        for(int i=0;i<=cnt;i++){    //枚举当前段的选择的个数，最少0个，最多cnt个，i是个数
            dfs(nums,k);  //往下一段递归,u更新为k,k即是下一段的开始位置。
            path.push_back(nums[u]);    //每次枚举完之后记得在当前方案中加一个当前数nums[u]

        }
        for(int i=0;i<=cnt;i++){
            path.pop_back();    //恢复现场
        }
    }
};

或者：我们还可以和79一样，按照当前位置这个数选或者不选来dfs。

算法思路
在LeetCode 78. 子集 中我们知道求子集问题与求全排列问题 的区别在于我们不需要考虑每个数在的位置或每个位置上是什么数，我们只在乎每一个数选或不选。因此对于有重复元素的子集问题，我们的思路不再像全排列那样关心每个数的先后关系，我们只需要关心相同的数选几个。具体步骤如下：

1. 将原数组排序，目的是将相同元素放在一起，之后好计算每个相同数的个数
2. 计算出当前数相同的个数，然后分别做出不选，选1个，选2个…的选择，然后递归到下一层
3. 注意在每做完一个选择递归到下一层时不需要马上回溯，因为我们选1个，选2个…每一个之后的选择是建立在之前选择上多选一个，所以我们不需要马上回溯
4. 当做出所有选择后，我们才需要将选择的这一段相同的数清空，所以回溯需要在做完所有选择后再进行
   这个分析代码在下面：

代码：

class Solution {
public:
    vector<vector<int>> res;    //记录答案 
    vector<int> path;   //path记录当前方案
    vector<vector<int>> subsetsWithDup(vector<int>& nums) {
    	//一定不要忘记写排序。
        sort(nums.begin(),nums.end());  //先对数组进行排序，之后可以方便的计数数组中相同元素的个数
        dfs(nums,0);    //从第0段开始枚举
        return res; //将答案返回
    }
    void dfs(vector<int>& nums,int u){  //u是枚举到数组的当前段
        if(u==nums.size()){ //枚举完全段，说明我们找到了一组答案。
            res.push_back(path);
            return;
        }
        //否则我们就需要找一下当前段中数的个数
        int k=u+1;
        while(k<nums.size()&&nums[k]==nums[u])k++;  //k最后到达新端
        int cnt=k-u;    //当前段的个数
        dfs(nums, k); //当前这种数一个都不选,即直接递归到下一层
        for(int i = 1; i <=cnt; i++) //分别选1个,2个,...,cnt个
        { 
            path.push_back(nums[u]); 
            dfs(nums, k);
        }
        //注意是path数组，这里和nums数组没有关系。
        path.erase(path.end() - (k - u), path.end()); //回溯，将选择的这一段相同的数全部清空
    }
};

2021年8月26日12:43:33：

//这个题目和子集I不同的地方就是数组中可能包含重复元素，所以这个题目我们不能再使用二进制的方法，因为子集I中的每个数字只能选0次或者1次，和二进制对应
//而这个题目中的数字可能有多个，所以这个题目我们只能使用递归的方法解决，其实是告诉了我们每个数字的出现次数，然后返回子集
//我们先对数组排序，使用双指针枚举一下当前数的选取个数，仿照组合总数I,II那两个题目一样，枚举选取的个数，使用递归，记得回溯
class Solution {
    List<List<Integer>> res=new ArrayList<>();  //res记录答案
    List<Integer> path=new ArrayList<>(); //记录当前子集
    public List<List<Integer>> subsetsWithDup(int[] nums) {
        //排序勿忘
        Arrays.sort(nums);  //有重复元素的题目，一般都要先对数组进行排序，这个题目也不例外，我们先对数组nums进行排序
        dfs(nums,0);  //从数组的下标0开始爆搜
        return res; //递归结束，返回答案res
    }
    public void dfs(int[] nums,int u){ //编写外部dfs函数，u是当前枚举到了数组nums的哪一位
        if(u==nums.length){ //当枚举完了数组，我们就找到了一个子集path，加到答案res中
            res.add(new ArrayList<>(path));
            return; //递归结束语句，return;不可不写
        }
        //因为nums数组已经排好序了，所以我们可以使用双指针算法数一下当前数的有几个，使用双指针还有一个好处，即再往下递归的时候，下标k就直接有了
        int k=u+1;  //从u的下一位开始判断，看数组中有几个nums[u],
        while(k<nums.length&&nums[k]==nums[u]) k++; //经典的双指针求相同数的个数的while迭代写法，当停下来的时候，k到达新的数的第一个位置，即下一个要递归的位置
        int cnt=k-u; //数组中的nums[u]的个数就是k-u个
        for(int i=0;i<=cnt;i++){ //我们枚举一下当前数nums[u]可以选几个，可以一个都不选，最多可以选cnt个，所以这里的枚举个数i就可以从0到cnt[0,cnt],左闭右闭
            dfs(nums,k);  //往下一个位置上的新数递归，新数的第一个下标是k
            path.add(nums[u]);  //每循环一次就加到path中一个nums[u],因为i是从0开始枚举的，即最开始是选0个nums[0],即一个nums[u]都不选，
            //所以我们这里把dfs(nums,k)放到上面就实现了当是选0个nums[u]的时候，不往path中添加nums[u]的目的，这一点很巧妙
        }
        //回溯，加了几个nums[u]就要去除几个nums[u]
        for(int i=0;i<=cnt;i++){
            path.remove(path.size()-1); 
        }

    }
}

算法二：更好理解版本：

算法分析
先对数组从小到大排序，每个数有选和不选两种情况，若选的话，假设上一个数与当前数一致，且上一个数没有选，则当前数一定不能选，否则会产生重复情况

class Solution {
    List<List<Integer>> ans = new ArrayList<List<Integer>>();
    List<Integer> path = new ArrayList<Integer>();
    boolean[] st;	//和前面y总讲的题目一样，我们这里开一个布尔数组，记录一下这个数是否被访问过，对于相同数，我们只使用第一个
    public List<List<Integer>> subsetsWithDup(int[] nums) {
        Arrays.sort(nums);
        int n=nums.length;
        st = new boolean[n];
        dfs(nums,0);
        return ans;
    }
    public void dfs(int[] nums,int u)
    {
        if(u == nums.length)
        {
            ans.add(new ArrayList<Integer>(path));
            return ;
        }

        //对于当前数，我们有选或者不选两种可能，选的话，记得回溯，
        //不放 ，先写不选，这个简单
        dfs(nums,u + 1);  //不选，直接往下递归即可

        //放
        if(u > 0 && nums[u] == nums[u - 1] && !st[u - 1]) return ; //不是第一个数，我们就跳过，注意这里我们没有放到循环中，所以不能写continue或者break,只能写return结束 
        st[u] = true; //标记这个数已经访问过
        path.add(nums[u]);  //将这个数加到当前子集path中
        dfs(nums,u + 1);  //继续往下一个数递归，注意这里我们已经判断只用相同数的第一个了，所以不用再找到新的数了，上面的if判断会跳过相同数
        path.remove(path.size() - 1); //下面两步是回溯操作
        st[u] = false;
    }
}

2021年10月23日14:06:45：

class Solution {

//因为要求所有的方案,并且包含重复的元素,即每一个数组不是只有选或者不选两种可能了,还可能选取多个,所以就不能使用二进制的方法了,直接dfs完成
//假设数组中的a[1]有c1个,则a[1]的选取情况就有0~c1(即a[i]选0个,1个，2个,...c1个),共c1+1种选取情况,a[2]有c2个，a[2]的选取情况就有c2+1种,...
//nums数组的所有子集的个数符合乘法原理，即一共(c1+1)*(c2+1)*...*(cn+1)个子集,我们先对数组排序，可以方便我们统计相同数的个数
//统计出来相同数的个数之后再枚举这个数选0个,1个,2个,...,c[i]个,然后对于每种情况递归，
//如果不太熟的话，可以画出递归搜索树，根节点的分支是a[1]的选取个数的情况:选0个a[1],1个,2个,...c1个,在对于每一个分支节点继续递归下去,
//比如选0个a[1]那个分支，我们可以接着选0个a[2],1个,2个,...,c2个,......
//这个题目不强调顺序，即相同数在不同顺序视为相同的子集，有点类似于组合的题目，而和排列问题不太像，即也是按顺序选数，和39,40题一样的套路

    List<List<Integer>> res=new ArrayList<>();
    List<Integer> path=new ArrayList<>();
    int[] num;
    int n;
    public List<List<Integer>> subsetsWithDup(int[] nums) {
        Arrays.sort(nums);  //先对数组排序，排序是接下来一切操作的基础，没有排序，一切都是白谈，
        num=nums;
        n=num.length;
        dfs(0); //从nums数组的第0个位置可以选取(更确切说是从nums数组的第0段开始枚举)
        return res; //递归结束返回的时候输出res答案数组
    }
    public void dfs(int u){ //在dfs的过程中完成数组子集的求取,u是当前枚举到了nums数组的哪一个元素的下标
        if(u==n){ //已经枚举完了所有的数
            res.add(new ArrayList<>(path));
            return;
        }
        //否则我们就来求一下当前这一段数字有多少个
        int k=u;
        while(k<n&&num[k]==num[u]) k++;
        int cnt=k-u;  //当前这一段数字的个数是k-u个
        //下面的代码就和y总写组合总和的代码很相似了，即枚举枚举数字选几个，只不过限制条件是选取个数k<=cnt
        for(int i=0;i<=cnt;i++){  //枚举一下当前数选几个，即这里i枚举的是当前数选几个，最少是0个，最多是cnt个
            dfs(k); //继续往下递归，k是nums数组下一段的第一个数的下标
            path.add(num[u]); //选择一个nums[u]就往path中添加一个num[u],把dfs(k)放到path.add(num[u])的上面就实现了选0个num[u],
            //即不选择num[u]直接往下递归的操作，
        }
        //下面进行回溯操作，选了几个num[u]就要从path中去除几个,即我们已经添加了cnt个当前数，我们就要去除cnt个当前数
        for(int i=0;i<=cnt;i++){  //这里的操作还是和39,40题选取组合总和的题目是相同的
            path.remove(path.size()-1);
        }
    }
}

方法二：

class Solution {
    List<List<Integer>> res=new ArrayList<>();
    List<Integer> path=new ArrayList<>();
    int[] num;
    boolean[] st;
    int n;
    public List<List<Integer>> subsetsWithDup(int[] nums) {
        Arrays.sort(nums);
        num=nums;
        n=num.length;
        st=new boolean[n];
        dfs(0);
        return res;
    }
    public void dfs(int u){
        if(u==n){
            res.add(new ArrayList<>(path));
            return;
        }
        //不放当前数
        dfs(u+1);  //注意下面有if判断不会先使用后面的相同数，所以这里就不用判断了
        //放当前数
        if(!st[u]){ //只有当前数还没有使用的时候，我们才能使用当前数
            if(u>0&&num[u]==num[u-1]&&!st[u-1]) return; //前一个相同数还没有使用的话，则这个数就不能使用，我们应该先跳过这种情况，而这里没有循环，所以不能写continue,而应该是写return;
            path.add(num[u]);
            st[u]=true;
            dfs(u+1);
            st[u]=false;
            path.remove(path.size()-1);
        }
    }
}

93. 复原 IP 地址

给定一个只包含数字的字符串s，用以表示一个 IP 地址，返回所有可能从 s 获得的 有效 IP 地址 。你可以按任何顺序返回答案。

有效 IP 地址 正好由四个整数（每个整数位于 0 到 255 之间组成，且不能含有前导 0），整数之间用 '.' 分隔。

例如："0.1.2.201" 和 "192.168.1.1" 是 有效 IP 地址，但是
"0.011.255.245"、"192.168.1.312" 和 "192.168@1.1" 是 无效 IP 地址。

示例 1：

输入：s = "25525511135"
输出：["255.255.11.135","255.255.111.35"]

示例 2：

输入：s = "0000"
输出：["0.0.0.0"]

示例 3：

输入：s = "1111"
输出：["1.1.1.1"]

示例 4：

输入：s = "010010"
输出：["0.10.0.10","0.100.1.0"]

示例 5：

输入：s = "101023"
输出：["1.0.10.23","1.0.102.3","10.1.0.23","10.10.2.3","101.0.2.3"]

提示：

0 <= s.length <= 3000
s 仅由数字组成

算法分析：

算法分析
暴力枚举dfs

一共有4位数字，暴力枚举4个在[0,255]区间合法数字，若当前枚举的数字符合条件，则再从下一个位置开始枚举下一个数字。

我们搜索的时候需要考虑搜索顺序是什么，我们先搜索第一个数，再搜索第二个数，再第三个数，最后第四个数。每个数都要满足范围在0~255并且没有前导0。但是单独的一个零是可以的，即0可以，但是01不可以。

**DFS爆搜，搜第一个数到第四个数，确保分割后每个数字：

1. 在0~255之间
2. 没有前导0**

DFS(字符串s，当前搜到串u号位置，当前搜到k号数，当前搜索出的结果字符串path)

代码：

class Solution {
public:
    vector<string> ans;   //定义答案数组
    vector<string> restoreIpAddresses(string s) {
    	// 参数2: 第i个数(字符串下标，最多有s.size()个), 参数3: 第k个字符
        dfs(s,0,0,"");    //刚开始递归，传入参数是被搜索字符串，从第0位开始递归，一开始整数为0个，一开始第一个路径为空""。
        return ans;   //递归全部结束，将答案返回。
    }
    //每次都新建path，所以这里不需要回溯操作。
    void dfs(string s,int u,int k,string path){   //s为要搜索的字符串，u是当前搜索到哪个下标，k是第几个整数，（最多4个），path表示当前方案是什么。
    	//  搜到结果
    	// 必须4个字段且整个字符串都用到，才是合法方案
        if(u==s.size()){
            if(k==4){   //如果字符串已经搜索完毕并且正好是有4个数组成就说明已经找到了一组方案，就将这组方案加到答案数组中。
                //第29行每个整数后都加了".",但是最后一个数字后面不能加".",所以这里我们在将当前方案加到答案数组之前要去掉最后一个"."
                path.pop_back();	// 去掉末尾的'.'
                ans.push_back(path);  //将当前方案加到答案数组中去。
                return;    //结束本次递归
            }
        }
        // 剪枝，如果已经搜完了四个数，但是s没用完就不搜了
        if(k==4) {  //如果已经组成了4个整数但是u还没有到达最后，说明至少有5位数字，不符合要求，直接提前结束本次递归，即是剪枝，很重要。s最多有3999位。
            return;   //剪枝，即提前结束本次递归。
        }
        //否则的话，即还不到4位数字，我们就正常递归即可，即此时我们搜索的是第k位上的数字
        for(int i=u,t=0;i<s.size();i++){    //从第u位开始递归，t记录第k位上的数字。
        	// 检查前导零，不能有前导零
            if(i>u&&s[u]=='0') break;   //如果第k位上的数字至少有两位（i>u）,并且有前导0(s[u]=='0)，我们就可以认定本次for循环不符合要求，我们就直接让第k位上的数字为0。
            //否则的话，我们计算一下第k位上的数字是多少，即每次把个位空出来, 将t*10即可
            t=t*10+s[i]-'0';    //更新记录一下第k位上的数字。//当前分割出来的数
            //for循环的过程中，if和else选择一个执行。
            if(t<=255) dfs(s,i+1,k+1,path+to_string(t)+".");    //如果第k位上的数<=255(不用判断>=0,因为t初始化为0，不可能会<0),我们就继续往下一位继续递归，
            //并将u更新为i+1,再递归时第k+1位数字，并且将数字t变成字符串加到当前方案中去,别忘了加"."。
            // 已经大于255了，不用再往后搜了
            else break;    //否则就大于了255,一定不符合题目要求。我们直接结束本次for循环。
        }
    }
};

暴力法：

class Solution {
public:
    vector<string> restoreIpAddresses(string s) {
        vector<string> res;

        for (int a = 1; a < 4; a ++ )
            for (int b = 1; b < 4; b ++ )
                for (int c = 1; c < 4; c ++ )
                    for (int d = 1; d < 4; d ++ )           //abcd分别表示四段ip地址长度
                    {
                        if (a + b + c + d == s.size())      //四段长度刚好
                        {
                            string s1 = s.substr(0, a);     //分别截取四段ip地址
                            string s2 = s.substr(a, b);
                            string s3 = s.substr(a + b, c);
                            string s4 = s.substr(a + b + c);

                            if (check(s1) && check(s2) && check(s3) && check(s4))
                            {
                                string ip = s1 + '.' + s2 + '.' + s3 + '.' + s4;
                                res.push_back(ip);
                            }
                        }
                    }

        return res;
    }

    bool check(string s)        //判断ip地址每段的第一位不为0，或只有一位且该位为0
    {
        if (stoi(s) <= 255)
            if (s[0] != '0' || (s[0] == '0' && s.size() == 1)) return true;

        return false;
    }
};

java代码：

class Solution {
    List<String> res=new ArrayList<>();
    public List<String> restoreIpAddresses(String s) {
        int n=s.length();
        if(n<=3) return res;
        dfs(s,0,0,"");
        return res;
    }
    void dfs(String s,int u,int k,String path){
        if(k==4){
            if(u==s.length()){
                String st=path.substring(0,path.length()-1);  //这里用substring去除最后一位。	//注意由于java中Sting类是不可变类，这里不可以直接让path=path.substring(0,path.length()-1);,path是不会变的，只能重新申请新的字符串。
                res.add(st);
            }else return;	//这个剪枝非常重要！！！
        }
        for(int i=u,t=0;i<s.length();i++){
            if(i>u&&s.charAt(u)=='0') break;
            t=t*10+s.charAt(i)-'0';
            String str=""+t+".";
            if(t<=255) dfs(s,i+1,k+1,path+str);
            else break;
        }
    }
}

二刷93题

//从前往后，一位一位的搜，注意**剪枝**
class Solution {
public:
    vector<string> res;    //记录答案
    vector<string> restoreIpAddresses(string s) {
        dfs(s,0,0,"");	//从第0位开始搜，当前搜的是第0个数。
        return res;
    }
    void dfs(string s,int u,int k,string path){    //dfs函数，u是字符串s的下标，k是搜索到第几个数，path是当前方案
        if(u==s.size()){    //如果最后一位也满足且正好是4个数，就说明我们找到了一组方案。
            if(k==4){
                path.pop_back();	//去掉最后一个点
                res.push_back(path);
                return;
            }
        }
        //剪枝
        if(k==4) return;    //如果已经找到了4个数但是字符串还没有枚举完，说明肯定不是合法的方案，我们提前结束
        //下面就是正常的递归，我们就搜索一下第k位上的数字
        for(int i=u,t=0;i<s.size();i++){    //第k位数字从字符串第u位开始，t表示当前位上数值是多少
            if(i>u&&s[u]=='0') break;    //有前导0
            t=t*10+s[i]-'0';    //求出当前位上的数
 //注意往下递归的时候，更新为i+1,不是u+1,因为u是不变的，比如当此时第k位选了2位，则应该从第3位枚举第k+1为，而u还是0，所以是i+1.
            if(t<=255) dfs(s,i+1,k+1,path+to_string(t)+'.');    //如果for循环过程中，找到了一个合法的第k位上的数字(没有前导0，在0~255之间)，我们就需要尝试判断一下这样行不行。
            else break; //如果>255，说明一定不合法，我们提前结束即可。
        }
    }
};

2021年9月1日18:06:58：

//dfs进行爆搜，有两个条件：1.数字在0~255之间，2.每一段都不能有前导0，
//分析一下时间：首先字符串长度n最多12位，如果n大于12位就一定不是合法IP地址，所以n一定是<=12,我们考虑最坏情况下，即n=12位，我们考虑那三个点
//可以放的位置有11个，共3个点，所以总情况个数就是C11,3  再加复制方案的O(n)的复杂度就是O(C11,3 *n)，即是O(Cn,3 *n)
class Solution {
    List<String> res=new ArrayList<>(); //记录答案
    public List<String> restoreIpAddresses(String s) {
        int n=s.length();
        if(n>12||n<4) return res;  //如果字符串长度大于12或者小于4，一定不存在合法的IP地址，我们返回空数组
        dfs(s,0,0,""); //爆搜一下，第一个0表示当前搜到的数的下标是0，第二个0表示当前要组的是第几个数，共4个，当前路径是空，即""
        return res; //递归结束之后将答案返回
    }
    public void dfs(String s,int u,int k,String path){ //u表示当前搜到第几个数了，k表示当前组到第几个数了，共4个数，path是当前路径方案,
        //因为我们每次是传入的新的path，所以这个题目不需要回溯操作
        if(k==4){  //如果当前正好组了4个数，至于这里为什么是4，道理和下面的u==s.length()一样，因为往下递归的时候递归参数都是往后一个,还需要看一下字符串是否正好枚举完毕
            if(u==s.length()){ //如果当前已经搜完了所有位,我们就找到了一条路径，我们就把path加到res中
                path=path.substring(0,path.length()-1); //因为在下面我们在每个段后都添加了'.',但是最后一段之后是不需要'.'的，所以我们在将path添加到res之前，需要先将最后一个'.'去掉
                res.add(path);  //将path加到res中
            }else{
                return; //而如果已经组好了四个数，但是字符串还没有结束，我们就直接结束，这是一个剪枝操作，通过这个剪枝我们就可以把那些长度大于12的去掉，上面已经判断过了，其实这里可以不用写
            }
        }
        //否则我们就来组一下第k个数到底是什么
        for(int i=u,t=0;i<s.length();i++){  //从字符串的第u位开始,t记录当前第k个数值是多少
            //如果有前导0
            if(i>u&&s.charAt(u)=='0') break;  //这里i>u&&s.charAt(u)=='0'表示数位不止一位并且第一位是0，即含有前导0，就说明不是一种合法的方案，我们直接break掉
            //而这里必须要加上i>u的意思是说，如果是一个一位数并且是0,这种情况是可以的，但是如果第2,3,4位数并且第一位再是0的话就是不合法的
            t=t*10+(s.charAt(i)-'0');  //否则我们就要更新t值，即先乘以10将这一位空出来，再加上这个数
            if(t<=255&&t>=0) dfs(s,i+1,k+1,path+t+".");  //如果t在0~255之间，我们就继续往下一位递归，注意枚举到的字符串的下标是i+1了，不是u+1,
            //而需要组的数是第k+1个，当前路径是path+t,注意'.'需要我们自己添加上，
            else break; //否则如果t大于255，我们也是直接终止
        }
    }
}

95. 不同的二叉搜索树 II

给定一个整数 n，生成所有由 1 ... n 为节点所组成的 二叉搜索树（二叉排序树） 。

示例：

输入：3
输出：
[
  [1,null,3,2],
  [3,2,null,1],
  [3,1,null,null,2],
  [2,1,3],
  [1,null,2,null,3]
]
解释：
以上的输出对应以下 5 种不同结构的二叉搜索树：

   1         3     3      2      1
    \       /     /      / \      \
     3     2     1      1   3      2
    /     /       \                 \
   2     1         2                 3
 

提示：

0 <= n <= 8

算法思路：

一般关于二叉树的问题都可以用递归来解决， 同时二叉搜索树又是一种根据递归定义的树，所以此题可由递归来求解。

对于一棵二叉搜索树来说，一个重要的性质就是它的中序遍历为升序，中序遍历的过程为：左 -> 根 -> 右，如果给每个结点标记上编号，意思就是说所有左子树节点的编号一定小于根节点，所有右子树的结点编号大于根节点。在此题中给定了一个中序遍历顺序1 ~ n， 于是我们的思路如下：

1. 先枚举根节点的位置，将问题划分为分别递归求解左边子树和右边子树
2. 递归返回的是所有合法方案的集合，所以枚举每种合法的左右儿子
3. 枚举左右儿子和根节点作为一种合法方案记录下来

首先：思路上总体是基于递归和分治的一个思想

1.为什么我们每次选择了根节点之后形成的树一定是二叉搜索树?

因为本身给的数的序列就是有序的

在递归树的每一层保证了左子树一定小于根节点,右子树一定大于根节点，那么我们就递推的得到了整棵树都是符合二叉搜索树定义的预期的。

2.
其次用来存储答案的vector<TreeNode>res用的也很讲究,它在每一层递归的时候将该层的所有情况的根节点返回，返回后将这个变量空间释放后又重新开辟出了这个变量，将它作为左子树的子情况或者右子树的子情况分别用for语句重新遍历，并且用乘法原理相结合。这样开辟空间也非常nice.*

算法
(分治、枚举) O(卡特兰数∗n)

这题跟Leetcode22括号生成非常类似；
使用分治来枚举；
枚举过程中可以用记忆化搜搜来优化其实，不过数据范围比较少，这样分治枚举已经足够了。

时间复杂度
一共卡特兰数个方案，每一次需要O(n)，所以总复杂度是O(卡特兰数∗n)

(dfs暴搜)

• 中序遍历的序列都是递增的，所以根节点左右两边的子树也都是二叉搜索树
• dfs的返回值设置为[l,r]序列中能组合出的二叉搜索树
• 先确定根节点的位置，然后分别对左右序列进行dfs搜索，获取左右子树的组合集合，并进行树的连接。
• 如果序列中没有元素，则添加一个null元素，作为递归基。

递归。

对连续的区间 [l, r] ，枚举二叉搜索树的根节点，假设当前为 i ：

分别递归求左右子树的所有方案 [l, i - 1] 和 [i + 1, r] 左子树的任意一种方案可以和右子树的任意一种方案拼接在一起，以
i 为根节点即可组成区间 [l, r] 上的一棵二叉搜索树

在中序遍历里，二叉搜索树的某一棵子树一定对应排好序的数组里连续的一段。所以只需要对区间[L,R]枚举每个点K作为根结点，那么左子树就对应区间[L,K−1]，右子树就对应区间[K+1,R]，从而变成递归问题。

那么当前以K位置作为根结点，方案数就是左子树方案数乘以右子树方案数。要给出方案，那就是左子树取一个方案，右子树取一个方案，然后把它们拼起来。

//相同结构子树不会被重复创建。

代码：

class Solution {
public:
    vector<TreeNode*> generateTrees(int n) {
       if(n==0) return {NULL};  //特判，如果n为0，返回空
       return dfs(1,n); //n不为0，我们从1到n开始枚举根节点进行递归。
    }
    //返回在区间[l, r]中所有合法方案
    vector<TreeNode*> dfs(int l,int r){ //编写递归函数（l,r是递归的左右边界）,即是递归/当前区间的左右边界，从l~r枚举根节点
        if(l>r) return{NULL};   //如果l大于了r，说明当前子树一个节点也没有，我们返回空即可，这也是递归结束条件
        vector<TreeNode*> res;  //数组res存储当前子树
        for(int i=l;i<=r;i++){  //枚举根节点的位置,注意这是递归，不要写死了，注意是从l到r,不是1到n。则当前根节点就是i
            //左子树的区间
            auto left=dfs(l,i-1);  //返回左子树所有合法方案
            //右子树的区间
            auto right=dfs(i+1,r);  //返回右子树所有合法方案
            for(auto l:left){   //任取一棵左子树
                for(auto r:right){  //任取一棵右子树
                    // 拼成一棵树并加入结果
                    auto root=new TreeNode(i);  //创建出根节点，根节点的权值就是i,
 //注意我们每次都要重新创建根节点因为我们push_back的是指针，不重新创建，则每次push_back的指针都相同，则值也相同。
                    root->left=l,root->right=r; //根节点的左子树就是l,根节点的右孩子就是r
                    //加入以该结点为根的合法方案
                    res.push_back(root);    //拼成一棵子树,将当前根节点加入数组中即可。

                }
            }

        }
        return res;	//返回合法方案。
    }
};

java代码：

class Solution {
    public List<TreeNode> generateTrees(int n) {
        if(n==0) return new ArrayList<>();
        return dfs(1,n);
    }
    public  List<TreeNode> dfs(int l,int r){
        List<TreeNode> res=new ArrayList<>();
        if(l>r) {
            res.add(null); // 这里不能直接返回 emptyList，不然无法遍历，导致无法构造树结构
            return res;
        }
        
        for(int i=l;i<=r;i++){
            List<TreeNode> left=dfs(l,i-1);
            List<TreeNode> right=dfs(i+1,r);
            for(TreeNode x:left){
                for(TreeNode y:right){
                //这里每次都要新new出一个根节点。因为每次添加的都是根节点，根节点不能相同
                    TreeNode root=new TreeNode(i);
                    root.left=x;root.right=y;
                    res.add(root);
                }
            }
        }
        return res;
    }
}

126. 单词接龙 II (图论DFS+BFS)

给定两个单词（beginWord 和 endWord）和一个字典列表 wordList，找出所有从 beginWord 到 endWord 的最短转换序列。转换需遵循如下规则：

1. 每次转换只能改变一个字母。
2. 转换后得到的单词必须是字典列表中的单词。

说明:

• 如果不存在这样的转换序列，返回一个空列表。
• 所有单词具有相同的长度。
• 所有单词只由小写字母组成。
• 字典中不存在重复的单词。
• 你可以假设 beginWord 和 endWord 是非空的，且二者不相同。

示例 1:

输入:
beginWord = "hit",
endWord = "cog",
wordList = ["hot","dot","dog","lot","log","cog"]

输出:
[
  ["hit","hot","dot","dog","cog"],
  ["hit","hot","lot","log","cog"]
]

示例 2:

输入:
beginWord = "hit"
endWord = "cog"
wordList = ["hot","dot","dog","lot","log"]

输出: []

解释: endWord "cog" 不在字典中，所以不存在符合要求的转换序列。

算法分析：
图论:最短路问题，当边权值为1时，可以使用BFS来求解最短路问题。

127. 单词接龙

字典 wordList 中从单词 beginWord 和 endWord 的 转换序列 是一个按下述规格形成的序列：

• 序列中第一个单词是 beginWord 。
• 序列中最后一个单词是 endWord 。
• 每次转换只能改变一个字母。
• 转换过程中的中间单词必须是字典 wordList 中的单词。

给你两个单词 beginWord 和 endWord 和一个字典 wordList ，找到从 beginWord 到 endWord 的 最短转换序列 中的 单词数目 。如果不存在这样的转换序列，返回 0。

示例 1：

输入：beginWord = "hit", endWord = "cog", wordList = ["hot","dot","dog","lot","log","cog"]
输出：5
解释：一个最短转换序列是 "hit" -> "hot" -> "dot" -> "dog" -> "cog", 返回它的长度 5。

示例 2：

输入：beginWord = "hit", endWord = "cog", wordList = ["hot","dot","dog","lot","log"]
输出：0
解释：endWord "cog" 不在字典中，所以无法进行转换。
 

提示：

1 <= beginWord.length <= 10
endWord.length == beginWord.length
1 <= wordList.length <= 5000
wordList[i].length == beginWord.length
beginWord、endWord 和 wordList[i] 由小写英文字母组成
beginWord != endWord
wordList 中的所有字符串 互不相同

2021年10月29日20:12:53：

class Solution {

//这个题目直接使用bfs求最短路问题就可以了，注意这个题目算上了起点，即我们要让距离加一，最后的答案要加一
//这个题目和最短基因距离那个题目一模一样

    //List<String> word;  //List可以作为哈希表使用，所以我们无需再开哈希表存储单词列表中的单词了
    //注意这个题目必须要用set哈希表存储，否则就会超时
    Map<String,Integer> map=new HashMap<>();  //哈希表map存储字符串状态到起始状态的距离，类似于八数码问题
   	Set<String> set=new HashSet();
    Queue<String> q=new LinkedList<>(); //bfs要用到的队列

    public int ladderLength(String b, String e, List<String> word) {
    	for(String s:word) set.add(s)
        q.add(b); //先将起始字符串加到队列中
        map.put(b,1);   //初始状态到初始状态的距离是1,这个题目是要加一的
        while(q.size()!=0){
            String t=q.poll();  //取出队头元素
            //String r=t; //和最短基因距离那个题目一样，我们每次在枚举更换字符的时候，要保证t是不变的，而下面我们在做操作的时候会改变字符串他，
            //所以我们先存储下来字符串t,当然了这里也可以不存储字符串t，直接和最短基因距离那个题目一样每次申请新的字符数组tc
            for(int i=0;i<t.length();i++){  //枚举字符串t的所有字符     
                char[] tc=t.toCharArray();
                for(char j='a';j<='z';j++){ //枚举从a到z的所有字符
                    tc[i]=j;  //把tc的第i个字符变成j
                    String s=new String(tc);  //改变字符之后的新的字符串为s
                    if(set.contains(s)&&!map.containsKey(s)){  //如果单词列表中有字符串s并且s还没有被遍历过，我们就要遍历这个字符串
                        map.put(s,map.get(t)+1);  //首先更新一下到起点的距离
                        q.add(s);   //其次要将字符串s加到队列中，一定要将s插到队列中，否则队列中就没有元素了
                        if(s.equals(e)) return map.get(s); //如果在过程中发现走到了终点，我们就及时返回到终点的距离
                    }
                }
            }
        }
        return 0;   //如果上面的迭代过程中都没有返回结果，就说明从起点没有办法到达，我们返回0
    }
}

130. 被围绕的区域（递归，flood fill 算法和200题很像）

给你一个 m x n 的矩阵 board ，由若干字符 'X' 和 'O' ，找到所有被 'X' 围绕的区域，并将这些区域里所有的 'O' 用 'X' 填充。

示例 1：

输入：board = [["X","X","X","X"],["X","O","O","X"],["X","X","O","X"],["X","O","X","X"]]
输出：[["X","X","X","X"],["X","X","X","X"],["X","X","X","X"],["X","O","X","X"]]
解释：被围绕的区间不会存在于边界上，换句话说，任何边界上的 'O' 都不会被填充为 'X'。
 任何不在边界上，或不与边界上的 'O' 相连的 'O' 最终都会被填充为 'X'。
 如果两个元素在水平或垂直方向相邻，则称它们是“相连”的。

示例 2：

输入：board = [["X"]]
输出：[["X"]]

提示：

m == board.length
n == board[i].length
1 <= m, n <= 200
board[i][j] 为 'X' 或 'O'

算法分析：
DFS

从外层出发，dfs深度遍历，将不被包围的'O'变成'#’，最后枚举整个二维数组，把'O'和'X'变成'X'，'#'变成'0'

(Flood Fill, 深度优先遍历) O(n*m)**

逆向考虑问题，我们先统计出哪些区域不会被攻占，然后将其它区域都变成'X'即可。

具体做法如下：

本题是典型的泛洪填充(flood fill)，其实就是我们可以想象有一个洪水去淹没这个矩阵，如果遇见X就被阻隔在外不能淹没，如果遇见O就能一路顺着所有相连的O这样流淌下去，这时我们就会发现，所有被X完全包围的O，它是永远也不会被洪水淹没的，所有没有被X完全包围的O，也就是边界上的O，以及与边界上的O直接相连的其他所有的O都会被洪水淹没。所以本题就是让你找出不会被洪水淹没的O，然后维持O值不变，其他地方都把它置为X就可以了。

时间复杂度分析：每个位置仅被遍历一次，所以时间复杂度是 O(n*m)

代码：

class Solution {
public:
    int n,m;    //n,m分别表示数组的长和宽，dfs函数中也要用到，所以这里我们定义为全局变量
    vector<vector<char>> board; //为了方便我们将数组board定义为全局数组
    int dx[4]={-1,0,1,0},dy[4]={0,1,0,-1};  //方向矩阵数组
    void solve(vector<vector<char>>& _board) {
        board=_board;  //把原数组_board赋给board数组，最后别忘了再把board数组重新赋给_board  
        n=board.size(); //数组长
        m=board[0].size();  //数组宽

        //下面开始爆搜一下四周，只有四周的点以及和四周的点相连的点才可以活下来：可以逃跑。
        // 第一列,最后一列处理
        for(int i=0;i<n;i++){
            if(board[i][0]=='O') dfs(i,0);  //如果第一列中有点为O,我们就爆搜一下这个点
            if(board[i][m-1]=='O') dfs(i,m-1);  //如果最后一列中有点为O,我们就爆搜一下这个点
        }

        // 第一行,最后一行处理
        for(int i=0;i<m;i++){
            if(board[0][i]=='O') dfs(0,i);  //如果第一行中有点为O,我们就爆搜一下这个点
            if(board[n-1][i]=='O') dfs(n-1,i);  //如果最后一行中有点为O,我们就爆搜一下这个点
        }

        //注意搜索的时候我们要防止重复搜索，所以我们要将搜索过的节点打上标记，如：#
        //递归全部结束，在递归函数中我们已经将不被包围的'O'变成'#'，最后枚举整个二维数组，把'#'变成'0'，剩下的'O'和'X'都变成'X'
        for(int i=0;i<n;i++){
            for(int j=0;j<m;j++){
                if(board[i][j]=='#') board[i][j]='O';
                else board[i][j]='X';
            }
        }
        _board=board;   //注意我们要把写完的作业再交给老师，让老师批改，即是我们改的是board数组，而原数组是_board，所以我们要把board重新赋给_board
        //注意这个题目返回值为空，所以这里我们不用写return语句了。
    }

    //下面编写dfs函数
    void dfs(int x,int y){
        board[x][y]='#';    //先将这个点标记为#,代表以及访问过
        for(int i=0;i<4;i++){   //枚举一下上，右，下，左四个方向
            int a=x+dx[i],b=y+dy[i];    //[a,b]代表下一个将要判断的方向的坐标
            if(a>=0&&a<n&&b>=0&&b<m&&board[a][b]=='O') //如果[a,b]均没有越界且为'O',我们就往[a,b]递归
                dfs(a,b);   //继续往[a,b]继续递归
        }
    }
};

2021年9月1日21:31:21：

//这个题目的意思即是说如果'O'被'X'围住了，我们就把被围住的'O'变成'X',这个题目考察的是洪水灌溉算法(flood fill),即是一种简单的dfs,即搜索所有的连通块，爆搜
//从每一个点开始，每次向周围几个连通的部分去搜索，把所有和当前块相连的找出来即可，要开一个判重数组，避免重复判断
//我们可以先找出来那些没有被包围的'O',然后把剩余的'O'变成'X'即可，那我们该如何找出来那些'O'没有被包围呐？我们从四个边界出发，将四个边界上的'O'能连通的'O'找出来
//标记一下，之后再将没有被标记的'O'变成'X'即可，我们可以开数组或者改变字符的方式避免重复枚举，
class Solution {
    int m,n;  //为了下面dfs的时候方便，我们将数组的长和宽定义出来
    int[] dx={-1,0,1,0},dy={0,1,0,-1};  //定义方向数组
    public void solve(char[][] board) {
        m=board.length;n=board[0].length; //求出数组的行数和列数,注意m,n上面已经定义过了，所以注意这里不要再重复定义了
        //先看最左和最右两列
        for(int i=0;i<m;i++){  //枚举每一行
            if(board[i][0]=='O') dfs(board,i,0); //枚举每一行的第一列,(i,0)是当前点的坐标，如果当前点是'O'的话，即从(i,0)点开始爆搜
            if(board[i][n-1]=='O') dfs(board,i,n-1);  //每一行的最后一列
        }
        //再看最上和最下面两行
        for(int i=0;i<n;i++){ //枚举每一列
            if(board[0][i]=='O') dfs(board,0,i);  //最上面那一行
            if(board[m-1][i]=='O') dfs(board,m-1,i);  //最下面那一行
        }   //注意这里四个角的元素可能被重复枚举，但是没事，因为我们下面是有判重数组的
        //在dfs中我们将所有的和边界上的'O'相连的'O'都标记为了'#',我们就剩下的没有被标记为'#',即被'X'包围的'O'标记为'X'
        for(int i=0;i<m;i++){
            for(int j=0;j<n;j++){
                if(board[i][j]!='#') board[i][j]='X';  //如果dfs结束之后当前位置上的字符不是'#',即是原本就是'X'或者是被'X'包围的'O',我们都改为'X'
                else board[i][j]='O'; //否则就是存活下来'O',我们改为'O'
            }
        }
    }
    public void dfs(char[][] board,int x,int y){ //编写dfs函数，(x,y)是当前遍历到的格子的坐标      
        //遍历到当前这个格子之后，先将其标记为'#'
        board[x][y]='#';
        for(int i=0;i<4;i++){   //枚举上下左右四个方向
            int a=x+dx[i],b=y+dy[i];  //(a,b)是之后要移动的格子的下标
            if(a>=0&&a<m&&b>=0&&b<n&&board[a][b]=='O'){ //如果(a,b)在范围内，并且是'O'的话，我们就继续往(a,b)递归
                dfs(board,a,b);
            }
        }
    }
}

2021年10月28日21:44:15：
bfs:

class Solution {
    char[][] g;
    boolean[][] st;
    Queue<int[]> q=new LinkedList<>();
    int n,m;
    int[] dx={0,1,0,-1},dy={1,0,-1,0};
    public void solve(char[][] board) {
        g=board;
        n=g.length;m=g[0].length;
        st=new boolean[n][m];
        for(int i=0;i<n;i++){
            if(!st[i][0]&&g[i][0]=='O'){
                bfs(i,0);
            }
            if(!st[i][m-1]&&g[i][m-1]=='O'){
                bfs(i,m-1);
            }
        }
        for(int i=0;i<m;i++){
            if(!st[0][i]&&g[0][i]=='O'){
                bfs(0,i);
            }
            if(!st[n-1][i]&&g[n-1][i]=='O'){
                bfs(n-1,i);
            }
        }
        for(int i=0;i<n;i++){
            for(int j=0;j<m;j++){
                if(g[i][j]=='*') g[i][j]='O';
                else g[i][j]='X';
            }
        }

    }
    public void bfs(int x,int y){
        q.add(new int[]{x,y});
        st[x][y]=true;
        g[x][y]='*';
        while(q.size()!=0){
            int[] t=q.poll();
            for(int i=0;i<4;i++){
                int a=t[0]+dx[i],b=t[1]+dy[i];
                if(a<0||a>=n||b<0||b>=m||st[a][b]||g[a][b]!='O') continue;
                q.add(new int[]{a,b});
                st[a][b]=true;
                g[a][b]='*';
            }
        }
    }
}

dfs:

class Solution {
    char[][] g;
    boolean[][] st;
    Queue<int[]> q=new LinkedList<>();
    int n,m;
    int[] dx={0,1,0,-1},dy={1,0,-1,0};
    public void solve(char[][] board) {
        g=board;
        n=g.length;m=g[0].length;
        st=new boolean[n][m];
        for(int i=0;i<n;i++){
            if(!st[i][0]&&g[i][0]=='O'){
                dfs(i,0);
            }
            if(!st[i][m-1]&&g[i][m-1]=='O'){
                dfs(i,m-1);
            }
        }
        for(int i=0;i<m;i++){
            if(!st[0][i]&&g[0][i]=='O'){
                dfs(0,i);
            }
            if(!st[n-1][i]&&g[n-1][i]=='O'){
                dfs(n-1,i);
            }
        }
        for(int i=0;i<n;i++){
            for(int j=0;j<m;j++){
                if(g[i][j]=='*') g[i][j]='O';
                else g[i][j]='X';
            }
        }

    }
    public void dfs(int x,int y){
        g[x][y]='*';
        for(int i=0;i<4;i++){
            int a=x+dx[i],b=y+dy[i];
            if(a>=0&&a<n&&b>=0&&b<m&&g[a][b]=='O'){
                dfs(a,b);
            }
        }   
    }
}

200. 岛屿数量（洪水灌溉算法）

给你一个由 '1'（陆地）和 '0'（水）组成的的二维网格，请你计算网格中岛屿的数量。

岛屿总是被水包围，并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。

此外，你可以假设该网格的四条边均被水包围。

示例 1：
输入：grid = [
  ["1","1","1","1","0"],
  ["1","1","0","1","0"],
  ["1","1","0","0","0"],
  ["0","0","0","0","0"]
]
输出：1

示例 2：

输入：grid = [
  ["1","1","0","0","0"],
  ["1","1","0","0","0"],
  ["0","0","1","0","0"],
  ["0","0","0","1","1"]
]
输出：3

提示：

m == grid.length
n == grid[i].length
1 <= m, n <= 300
grid[i][j] 的值为 '0' 或 '1'

算法分析：

其实就是求全连通的1的个数，我们使用flood fill算法，

(深度优先遍历) O(nm)

1. 从任意一个陆地点（‘1’）开始，即可通过四连通的方式，深度优先搜索遍历到所有与之相连的陆地，即遍历完整个岛屿。每次将遍历过的点清 0（g[i][j]='0'）。
2. 重复以上过程，可行起点的数量就是答案。

这题就是求 联通块 的数量。可以遍历 grid 中的每个元素，对每个 1 ，从该位置进行搜索，将与它相邻的 1 做一下标记即可。

时间复杂度
由于每个点最多被遍历一次，故时间复杂度为 O(mn)。

空间复杂度
最坏情况下(即是整个矩阵全是1），需要额外 O(mn) 的空间作为系统栈。

我们可以将二维网格看成一个无向图，竖直或水平相邻的 1 之间有边相连。

为了求出岛屿的数量，我们可以扫描整个二维网格。如果一个位置为 1，则以其为起始节点开始进行深度优先搜索。在深度优先搜索的过程中，每个搜索到的 1 都会被重新标记为 0。

最终岛屿的数量就是我们进行深度优先搜索的次数。

下面的图片展示了整个算法：

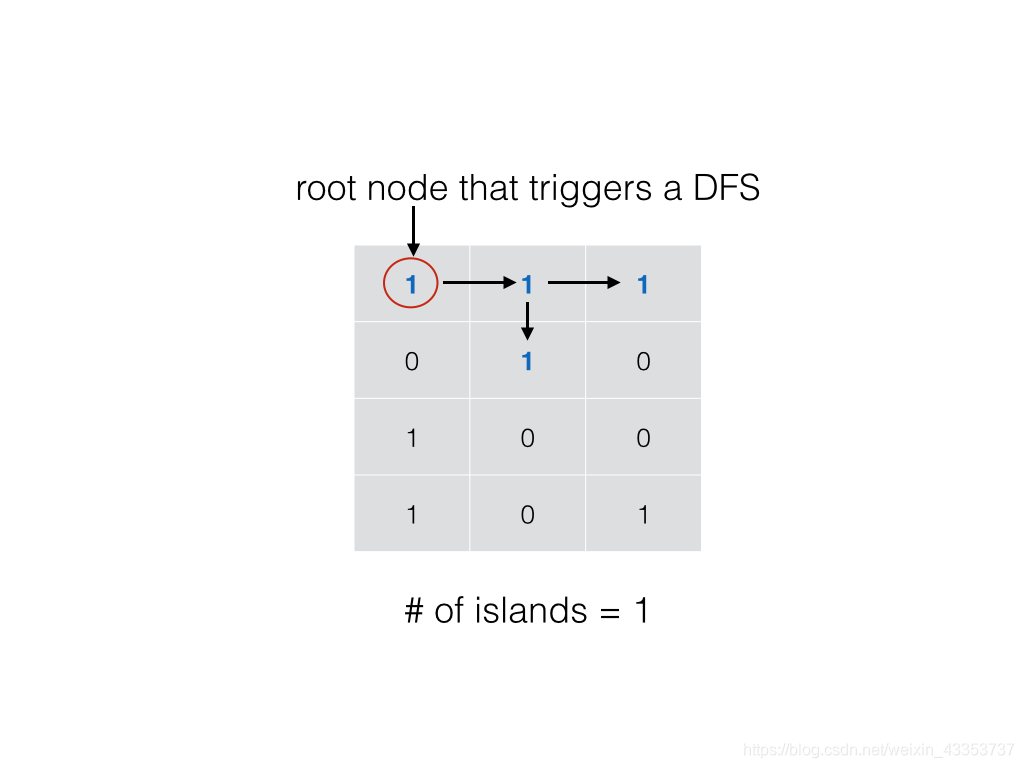
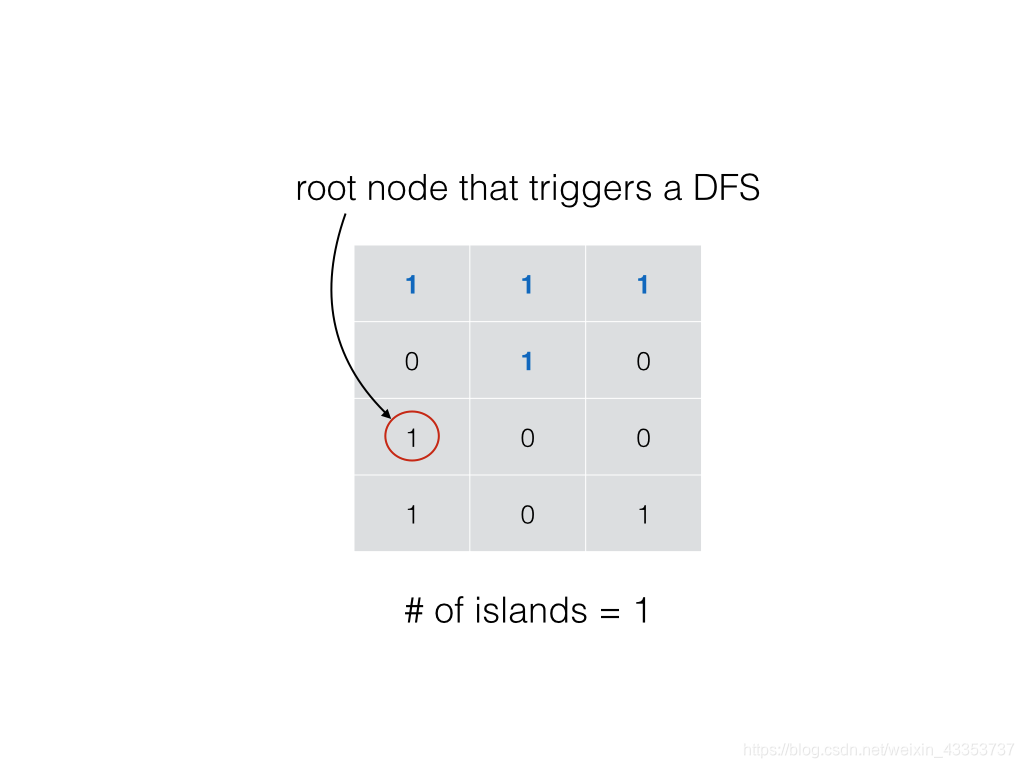
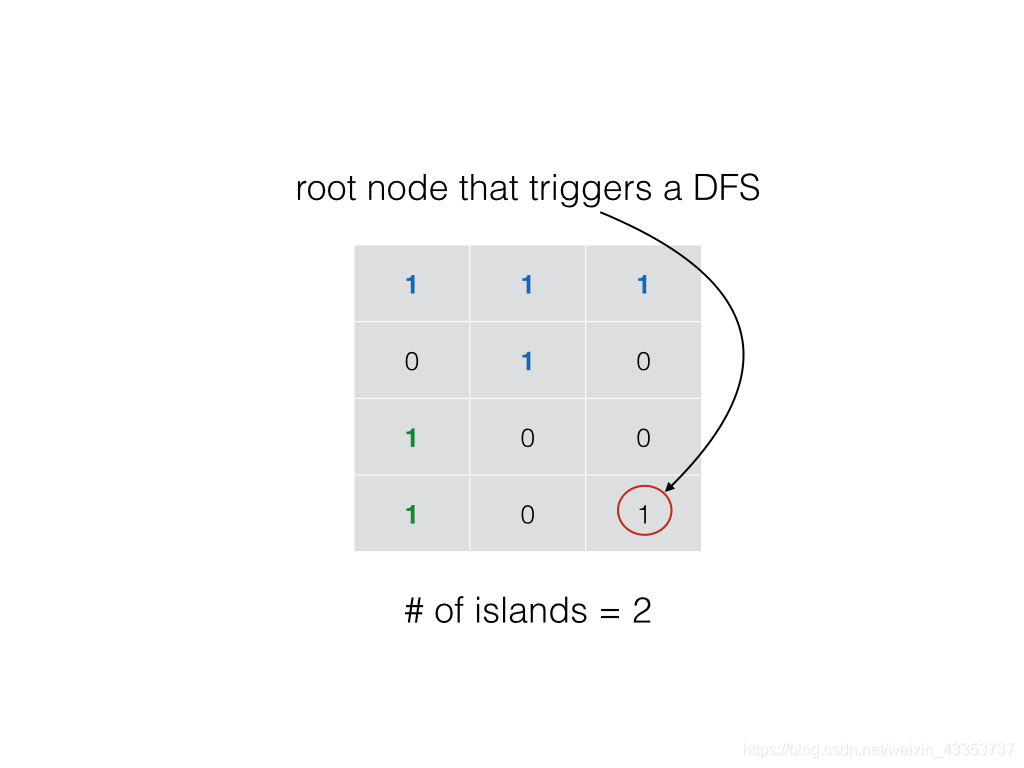
代码：

class Solution {
public:
    //这个题目其实就是求全流通的1的个数
    vector<vector<char>> g; //下面dfs函数也需要用到这个数组，所以这里我们将grid数组定义为全局的。
    int n,m;    //n,m分别是grid数组的行数和列数
    int dx[4]={-1,0,1,0},dy[4]={0,1,0,-1};  //方向矩阵
    int numIslands(vector<vector<char>>& grid) {
        g=grid; //把数组grid赋给数组g
        n=g.size(),m=g[0].size();   //求出数组的行数和列数
        int cnt=0;  //cnt记录全连通的1的个数
        for(int i=0;i<n;i++){   //每个点都作为枚举的起点，看一下其对应的全连通的1个数，
            for(int j=0;j<m;j++){
                if(g[i][j]=='1'){   //如果点（i,j）对应的点是'1'的话就进行dfs，dfs结束，cnt加一
                    dfs(i,j);
                    cnt++;
                }
            }
        }
        return cnt;
    }
    //下面就是具体的flood fill算法的编写，
    void dfs(int x,int y){
        g[x][y]='0';  //我们先将g[x][y]赋为'0',这样之后第13行代码就不会再重复dfs了，同时也保证了某一块全连通的1不会被重复计数
        for(int i=0;i<4;i++){   //接下来我们枚举(x,y)的四个方向
            int a=x+dx[i],b=y+dy[i];
            if(a>=0&&a<n&&b>=0&&b<m&&g[a][b]=='1') {   //如果点(a,b)是合法的(即没有越界而且还是'1'),我们就继续深搜(a,b)这个点
                dfs(a,b);
            }
        }
    }
};

2021年9月2日10:30:51：

//洪水灌溉算法，即简单的dfs问题，和130题很像，
//依次枚举一下每一个格子，如果(i,j)没有被遍历并且(i,j)是1，则遍历点(i,j)，之后往(i,j)的上下左右四个方向上递归，递归结束则count++,注意是在dfs函数中判重的
//洪水灌溉算法中每一个格子只会被遍历一次，所以时间复杂度就是O(n*m)
class Solution {
    int m,n;  //将数组的行数和列数定义为全局的，注意下面再对m,n赋值的时候就不要再写int了，否则下面的dfs中的m,n均是0，int型变量不赋初值则默认为0
    int[] dx={-1,0,1,0},dy={0,1,0,-1};  //定义方向数组
    public int numIslands(char[][] grid) {
        m=grid.length;n=grid[0].length; //求出数组的行数和列数，注意不要写int 了
        int cnt=0; //这个题目是让我们求出'1'连通块的数量，所以我们要定义一个答案
        for(int i=0;i<m;i++){ //枚举每一个格子
            for(int j=0;j<n;j++){
            	//注意一定要先判断grid[i][j]这个格子上是'1'的时候再去往下递归，不能直接往下递归否则cnt的个数计数就是错误的，因为这样的话cnt将会被累加m*n次
                if(grid[i][j]=='1'){  //如果这个格子是'1'的话，我们就从这个格子开始递归一下，下面dfs函数中我们有判重操作
                    dfs(grid,i,j); //从点(i,j)开始递归
                    cnt++; //每次循环递归结束之后就找到了一个'1'连通块
                }
            }
        }
        return cnt; //上面的递归结束之后最后将cnt返回
    }
    public void dfs(char[][] grid,int x,int y){
        grid[x][y]='0';  //先将这个节点改为'0',这样下面再判断的时候，因为这个格子上是'0',所以就不会再遍历这个格子了，这样也起到了去重的作用
        for(int i=0;i<4;i++){  //遍历一下四个方向上的格子
            int a=x+dx[i],b=y+dy[i];  //先看一下要移动的下一个方向的格子的坐标
            if(a>=0&&a<m&&b>=0&&b<n&&grid[a][b]=='1'){  //如果(a,b)没有越界并且是'1'，就往(a,b)递归
                dfs(grid,a,b);  //往(a,b)递归
                //dfs函数返回值是void,即我们不需要写return;结束语句
            }//注意这里else语句不用写，因为或者是越界或者是‘0’都是不符合题意的，我们就可以不用管
        }
    }
}

2021年10月28日21:42:59：

bfs:

class Solution {
    char[][] g;
    boolean[][] st;
    int n,m;
    Queue<int[]> q=new LinkedList<>();
    int[] dx={0,1,0,-1},dy={1,0,-1,0};

    public int numIslands(char[][] grid) {
        g=grid;
        n=g.length;m=g[0].length;
        st=new boolean[n][m];
        int res=0;
        for(int i=0;i<n;i++){
            for(int j=0;j<m;j++){
                if(g[i][j]=='1'&&!st[i][j]){
                    bfs(i,j);
                    res++;
                }
            }
        }
        return res;
    }

    public void bfs(int x,int y){
        q.add(new int[]{x,y});
        st[x][y]=true;
        while(q.size()!=0){
            int[] t=q.poll();
            for(int i=0;i<4;i++){
                int a=t[0]+dx[i],b=t[1]+dy[i];
                if(a<0||a>=n||b<0||b>=m||st[a][b]||g[a][b]=='0') continue;
                q.add(new int[]{a,b});
                st[a][b]=true;
            }
        }
    }
}

dfs:
其实dfs也可以不用开状态数组,每遍历一个‘1’，将其改为‘0’即可。

class Solution {

//方法二：使用dfs实现

    char[][] g;
    boolean[][] st;
    int n,m;
    int[] dx={0,1,0,-1},dy={1,0,-1,0};

    public int numIslands(char[][] grid) {
        g=grid;
        n=g.length;m=g[0].length;
        st=new boolean[n][m];
        int res=0;
        for(int i=0;i<n;i++){
            for(int j=0;j<m;j++){   //写法和bfs大体上相同，
                if(g[i][j]=='1'&&!st[i][j]){   //这个点是1并且没有被遍历过，我们就dfs一下这个点
                    dfs(i,j);
                    res++;  //dfs结束res++
                }
            }
        }
        return res;
    }

    public void dfs(int x,int y){
        st[x][y]=true;
        for(int i=0;i<4;i++){
            int a=x+dx[i],b=y+dy[i];
            if(a>=0&&a<n&&b>=0&&b<m&&g[a][b]=='1'&&!st[a][b]) {
                dfs(a,b);
            }
        }
    }

  
}

417. 太平洋大西洋水流问题(flood fill)

给定一个 m x n 的非负整数矩阵来表示一片大陆上各个单元格的高度。“太平洋”处于大陆的左边界和上边界，而“大西洋”处于大陆的右边界和下边界。

规定水流只能按照上、下、左、右四个方向流动，且只能从高到低或者在同等高度上流动。

请找出那些水流既可以流动到“太平洋”，又能流动到“大西洋”的陆地单元的坐标。

提示：

输出坐标的顺序不重要
m 和 n 都小于150

示例：

给定下面的 5x5 矩阵:

  太平洋   ~   ~   ~   ~   ~ 
       ~  1   2   2   3  (5) *
       ~  3   2   3  (4) (4) *
       ~  2   4  (5)  3   1  *
       ~ (6) (7)  1   4   5  *
       ~ (5)  1   1   2   4  *
          *   *   *   *   * 大西洋

返回:

[[0, 4], [1, 3], [1, 4], [2, 2], [3, 0], [3, 1], [4, 0]] (上图中带括号的单元).
 

2021年10月28日21:21:17：

class Solution {

//洪水灌溉算法,我们求的是哪些格子即可以到达太平洋也可以到达大西洋,我们反过来思考：我们从太平洋和大西洋出发可以到达哪些格子
//最后再枚举一下每一个格子看一下这个格子是否即可以从太平洋到,也可以从大西洋到,如果都可以的话,就是一个合法的格子
//我们怎么知道一个格子是否可以到哪？我们可以使用一个二进制的两位来表示,即_ _,00表示一个大洋都到不了,01表示只可以到太平洋,10表示只可以到达大西洋,11表示两个洋都可以到达
//即是用0表示一个大洋都到不了,1表示可以到太平洋,2表示可以到大西洋,3表示两个洋都可以到,这个题目使用dfs来解决

    List<List<Integer>> res=new ArrayList<>();
    int[][] h;
    int n,m;
    int[][] st; //st即表示每一个点的状态
    int[] dx={0,1,0,-1},dy={1,0,-1,0};
    public List<List<Integer>> pacificAtlantic(int[][] heights) {
        h=heights;
        n=h.length;m=h[0].length;
        st=new int[n][m];
        //先枚举太平洋的左边界和上边界
        for(int i=0;i<n;i++) dfs(i,0,1);  //左边界,点是(i,0),第三个参数是点的状态,从太平洋出发的,所以太平洋一定可以到达,所以状态值初始是1
        for(int i=0;i<m;i++) dfs(0,i,1);  //上边界,点是(0,i),初始状态也是1
        //再从大西洋出发,即右边界和下边界
        for(int i=0;i<n;i++) dfs(i,m-1,2);  //右边界，可以到达大西洋，所以初始状态是2
        for(int i=0;i<m;i++) dfs(n-1,i,2);  //下边界
        //递归全部结束的时候，我们再枚举每一个格子，如果格子的状态是3的话，就表示其两个洋都可以到
        for(int i=0;i<n;i++){
            for(int j=0;j<m;j++){
                if(st[i][j]==3){
                    List<Integer> path=new ArrayList<>();
                    path.add(i);
                    path.add(j);
                    res.add(path);
                }
            }
        }
        return res;
    }

    public void dfs(int x,int y,int t){ //dfs完成状态的关系
        //当前这个格子这一位上如果已经是1了，那么就说明已经遍历过了
        if((st[x][y]&t)!=0) return; //如果这个点的状态&上t不等于0的话(注意只能是不等于0，不能是等于1)，即已经被更新过了，
        //即表示这个格子已经被遍历过，我们直接return就可以了,
        st[x][y]|=t;  //否则的话我们就用t更新一下这个点的状态，即st[x][y]或上t
        for(int i=0;i<4;i++){  //再来枚举四个方向
            int a=x+dx[i],b=y+dy[i];  
            if(a>=0&&a<n&&b>=0&&b<m&&h[a][b]>=h[x][y]){ //(a,b)点没有越界并且高度>=(x,y)点，我们就可以往(a,b)点递归
                dfs(a,b,t); //我们就可以递归遍历，即dfs这个点(a,b),继续往下递归搜索
            }
        }
    }
}

695. 岛屿的最大面积

2021年11月21日15:51:06：

class Solution {

//这个题目就是提高课中的Flood fill算法的模板题,

    int[][] g;
    int n,m;
    int[] dx={-1,0,1,0},dy={0,1,0,-1};
    boolean[][] st;
    Queue<int[]> q=new LinkedList<>();

    public int maxAreaOfIsland(int[][] grid) {
        g=grid;
        n=g.length;m=g[0].length;
        st=new boolean[n][m];
        int res=0;  //res记录答案
        for(int i=0;i<n;i++){
            for(int j=0;j<m;j++){
                if(g[i][j]==1&&!st[i][j]) res=Math.max(res,bfs(i,j)); //bfs的返回值就是(i,j)点所在的岛屿的面积
            }
        }
        return res;
    }

    public int bfs(int i,int j){
        int res=0; //res记录的是(i,j)所在的岛屿的面积
        q.add(new int[]{i,j});  //先将点(i,j)加到队列中
        st[i][j]=true;  //把点(i,j)标记为已访问,其实这里把点(i,j)的值改为0就起到了标记为已访问的效果,而且这样就不用再开状态数组st了
        while(q.size()!=0){
            int[] t=q.poll();
            res++;
            for(int k=0;k<4;k++){
                int a=t[0]+dx[k],b=t[1]+dy[k];
                if(a<0||a>=n||b<0||b>=m||g[a][b]==0||st[a][b]) continue;
                q.add(new int[]{a,b});
                st[a][b]=true;
            }
        }
        return res; //最后返回的就是点(i,j)所在岛屿的面积
    }
}

131. 分割回文串

给你一个字符串 s，请你将 s 分割成一些子串，使每个子串都是 回文串 。返回 s 所有可能的分割方案。

回文串 是正着读和反着读都一样的字符串。

示例 1：

输入：s = "aab"
输出：[["a","a","b"],["aa","b"]]

示例 2：

输入：s = "a"
输出：[["a"]]
 

提示：

1 <= s.length <= 16
s 仅由小写英文字母组成

算法思路
dfs + 回溯

dfs算法的过程其实就是构建一棵递归树，所有的dfs算法的步骤大概有以下几步：

• 找到中止条件，即递归树从根节点走到叶子节点时的返回条件，此时一般情况下已经遍历完了从根节点到叶子结点的一条路径，往往就是我们需要存下来的一种合法方案
• 如果还没有走到底，那么我们需要对当前层的所有可能选择方案进行枚举，加入路径中，然后走向下一层
• 在枚举过程中，有些情况下需要对不可能走到底的情况进行预判，如果已经知道这条路不可能到达我们想去的地方，那我们干嘛还要一条路走到黑呢，这就是我们常说的剪枝的过程
• 当完成往下层的递归后，我们需要将当前层的选择状态进行清零，它下去之前是什么样子，我们现在就要让它恢复原状，也叫恢复现场。该过程就是回溯，目的是回到最初选择路口的起点，好再试试其他的路。

将上述思路运用在该题中：

1. 从第一个字符开始枚举，用path数组存储一条从递归树根节点到叶子结点的合法方案，用res数组存下所有的合法方案。
2. dfs过程的中止条件是当我们遍历完了所有字符，说明我们已经找到一条合法路径，此时将路径加入方案中。
3. 然后进行该层的选择枚举，这里枚举从该字符到结尾的所有长度，且该长度的字符串为回文串时，我们将其加入路径中，然后递归到下一层。
4. 当我们进行了下层的递归后，我们需要进行回溯，也就是恢复现场，目的是我们能够在该层重新做其他选择。
   （其对应的代码放到y总算法下面，即算法二）

时间复杂度 ：
长为n的字符串，有n−1个空，每个空都有断开或者不断开两种选择，所以是：O(2ⁿ)，又由于push_back( )的存在，所以总时间复杂度是：O(2ⁿ *n)。

• dp预处理每部分子串是否是回文串，注意数组的赋值顺序应该逐列赋值。
• 此题相当于在字符串中的各个位置放置板子来分割字符串，每个位置都有放与不放两种方式，指数级别时间复杂度。
• 指数级别的题目一般都是DFS暴搜
• 从第0个位置开始搜索，如果当前串是回文串，则从下个位置开始搜索，否则回溯。
  
  题解：首先我们预处理好哪些子串是回文串，这个可以用动态规划在O(n²)的时间内处理好，dp[i][j]代表s[i:j]是回文串。然后进行递归搜索，u代表当前处理到哪个位置，我们从当前位置开始，枚举所有可能的回文子串，进行递归搜索直至处理完整个字符串。最坏的情况是整个字符串都是同一个字符，这需要O(2ⁿ)时间复杂度。

代码：

class Solution {
public:
    vector<vector<bool>>  f;    //f[i][j]表示从i到j这一段是否是回文串。
    vector<vector<string>> res;    //定义全局答案
    vector<string> path;    //定义当前方案
    vector<vector<string>> partition(string s) {
        int n=s.size();
        f=vector<vector<bool>>(n,vector<bool>(n,false));    //初始化f数组均为false
        //下面我们对f数组进行赋值操作
        for(int j=0;j<n;j++){   // 必须先枚举j，这样f[i + 1][j - 1]才是先算好的
            for(int i=0;i<=j;i++){  //i是从0到j,表示从i到j这一段
                if(i==j) f[i][j]=true;  //如果i=j，说明只有一个字符，肯定是回文串，我们让f[i][j]=true;
                else if(s[i]==s[j]){    //否则如果s[i]=s[j],
                    if(i+1>j-1||f[i+1][j-1]==true) f[i][j]=true;    //如果只有两个元素(i+1>j-1)，或者f[i+1][j-1]==true，即前一段也是回文串，则f[i][j]也是回文串，更新完true
                }
            }
        }
        //其他情况均为false,但是我们不需要对其进行赋值，因为我们初始化f数组均为false
        dfs(s,0);   //从第0个字母开始爆搜
        return res;
    }
    void dfs(string s,int u){   //u表示搜索到字符串哪个下标了（即哪个字母）
        if(u==s.size()){    //当前方案已找到
            res.push_back(path);
            return;
        }
        else{   //否则的话，我们就需要枚举一下下一段是否是回文串
            for(int i=u;i<s.size();i++){    //
                if(f[u][i]==true){  //从u到i是回文串
                    //找一段回文串加入，而组合问题是每次加入一个数
                    path.push_back(s.substr(u,i-u+1));
                    //递归下一层
                    dfs(s,i+1); //往下一段递归。
                    path.pop_back();    回溯
                }
            }
        }
    }
};

算法二：

class Solution {
public:
    vector<vector<string>> res; //所有方案
    vector<string> path; //一个合法方案
    vector<vector<string>> partition(string s) {
        dfs(0, s); //从位置0开始dfs
        return res;
    }

    void dfs(int u, string s)
    {
        if (u == s.size()) //遍历完整个字符串
        {
            res.push_back(path); //将路径加入方案
            return;
        }

        for (int i = u; i < s.size(); i ++) //枚举从当前字符到结尾可以选择的长度
        {
            if (check(s, u, i)) //判断u ~ i是否为回文串
            {
                path.push_back(s.substr(u, i - u + 1)); //加入路径
                dfs(i + 1, s); //递归下一层
                path.pop_back(); //回溯
            }
        }
    }

    bool check(string s, int l, int r) //判断从l到r是否为回文串
    {
        while (l <= r)
        {
            if (s[l ++] != s[r --])
                return false;
        }

        return true;
    }
};

2021年9月1日19:52:15：

//爆搜，加一些剪枝优化，
class Solution {
    List<List<String>> res=new ArrayList<>();  //定义二维答案数组
    List<String> path=new ArrayList<>();  //定义一维的当前方案，注意就一个所以要记得回溯
    boolean[][] f;  //定义f数组，注意f数组是二维的
    public List<List<String>> partition(String s) {
        int n=s.length();
        f=new boolean[n][n];  //定义f数组的长度(因为i,j的下标都是0~n-1,所以长度都定义为n)并且布尔数组默认初始化为false
        //对所有的从i到j的字符串进行初始化，即判断从i到j这一段是否是回文串，我们发现先枚举j再枚举i就可以更新所有的从i到j的回文串情况，可以自己验证
        for(int j=0;j<n;j++){ //从小到大枚举下标j,
            for(int i=0;i<=j;i++){ //因为i在前，j在后，所以i最大是到j
                if(i==j) f[i][j]=true;  //如果只有一个字符一定是回文子串
                else if(s.charAt(i)==s.charAt(j)){  //如果s[i]=s[j]，这个时候还不能确定从i到j是否是回文串，还需要继续做判断
                    f[i][j]=(i+1==j)||(f[i+1][j-1]); //如果从i到j只有两个字符(i+1=j)并且两个字符相同(s[i]=s[j])或者是f[i+1][j-1]是回文串，则f[i][j]就是回文串
                    //所以i+1=j和f[i+1][j-1]之间是或的关系，并且当只有两个字符这种情况的时候(i+1=j)的时候要特判出来，不能和f[i+1][j-1]合并，因为如果只有两个字符则i+1和j-1会越界
                }
            }
        }
        //经过上面的枚举就可以把所有的从i到j是回文串的情况进行了更新，我们就开始递归
        dfs(s,0);  //0是当前枚举到了字符串s的哪一位
        return res; //递归结束之后就将答案进行返回
    }
    public void dfs(String s,int u){
        if(u==s.length()){  //正好找到了一组解，就把这组解加到答案中
            res.add(new ArrayList<>(path));
            return;
        }else{  //否则我们来枚举当前这一段是什么
            for(int j=u;j<s.length();j++){  //当前这一段的起点是u,终点是n-1
                if(f[u][j]){  //如果从u到j这一段是回文串的话，我们就把这一段加到path中，
                    path.add(s.substring(u,j+1)); //把从[u,j]这一段加到path中
                    dfs(s,j+1); //递归到下一层，即继续枚举下一段,注意下一段的起点是j+1，并且dfs函数没有返回值(void),所以不用写return
                    //记得回溯操作
                    path.remove(path.size()-1);
                }
            }
        }
    }
}

解法二：直接使用判断回文串的字符串的模板

class Solution {
public:
    vector<vector<string>> res;                 //都整成全局变量，免得回溯的时候传来传去的
    vector<string> tmp;

    vector<vector<string>> partition(string s) {
        dfs(s);
        return res;
    }

    void dfs(string s)
    {
        if (s.size() == 0)                      //字符串已经分割完，当前路径存到结果中
        {
            res.push_back(tmp);
            return;
        }

        for (int i = 1; i <= s.size(); i ++ )
        {
            string str = s.substr(0, i);
            if (check(str))
            {
                tmp.push_back(str);
                dfs(s.substr(i));               //去掉前i个字符，继续递归
                tmp.pop_back();                 //恢复现场
            }
        }
    }

    bool check(string s)                        //判断回文字符串模板
    {
        int l = 0, r = s.size() - 1;
        while (l <= r)
        {
            if (s[l] != s[r])
                return false;
            l ++ , r -- ;
        }

        return true;
    }
};

2021年9月9日13:29:08：

//考虑最坏情况下,当字符串是aaa...aaaaaa,即字符串中所有字符均相同的时候,我们此时有n-1个位置可以插入,每一个位置都可以作为分隔点,所以最坏情况下是2^(n-1)
//即是指数级别,当是指数级别的时候,我们就可以确定题目需要爆搜即dfs解决,爆搜的时候我们可以加一些优化剪枝
//我们在爆搜的时候，从字符串的第0个字符开始爆搜，当搜到最后一个字符的时候，就说明找到了一组解
class Solution {
    List<List<String>> res=new ArrayList<>(); //res记录答案
    List<String> path=new ArrayList<>();  //path是当前方案，path是全局的，所以记得回溯
    boolean[][] f;
    public List<List<String>> partition(String s) {
        int n=s.length();
        char[] c=s.toCharArray();
        f=new boolean[n][n];  //f[i][j]数组表示从i到j是否是回文串
        //我们现在为了更新从i到j这一段是否是回文串,即f[i][j]是否为true,需要先知道f[i+1][j-1],所以保证保证拓扑序,我们需要先从小到大枚举j，再从小到大枚举i
        for(int j=0;j<n;j++){  //判断从i到j这一段是否为true,我们需要先从小到大枚举j,之后再从小到大枚举i,注意f[0][0]=true,所以i,j均可以取到0,最大为n-1
            for(int i=0;i<=j;i++){ //再从小到大枚举i,注意i在j前，并且i可以和j重合，所以i的下标是从0到j,并且可以取到j
                if(i==j) f[j][i]=true; //如果i=j,即只有一个字符，一个字符一定是回文串，即f[i][j]=true
                else if(c[i]==c[j]){ //否则i就和j不相同，我们需要先保证s[i]=s[j],再看f[i+1][j-1]
                    if(i+1==j) f[i][j]=true; //如果下标i+1=j,上面这一段只有两个元素，并且这两个元素还是相同字符，则一定是回文串，即f[i][j]=true
                    else f[i][j]=f[i+1][j-1]; //否则f[i][j]是否为true,就取决于f[i+1][j-1]是否为回文串，即f[i+1][j-1]是否为true
                }
            }
        }
        dfs(s,0); //从字符串s的第0个字符开始搜
        return res; //递归结束之后返回res答案
    }
    public void dfs(String s,int u){ //u表示当前我们搜到第几位了
        if(u==s.length()){  //如果已经搜完了s字符串，我们就找到了一组解
            res.add(new ArrayList<>(path)); //将当前解加到答案中
            return;
        }else{ //否则我们来看一下字符串s下一段(或者说是当前段)是什么
            for(int i=u;i<s.length();i++){  //下一段的起点是u,终点是i，i最大是n-1,我们就需要看一下从u到i这一段是否是回文串
                if(f[u][i]==true) { //如果从u到i是回文串，我们就把从u到i这一段加到path中之后继续往字符串的下一个位置i+1递归
                    path.add(s.substring(u,i+1));  //这一段的起点是u,终点是i,所以截取的范围是[u,i+1)
                    dfs(s,i+1); //继续往下一个位置递归
                    path.remove(path.size()-1); //回溯       
                }
            }
        }
    }
}

133. 克隆图（哈希表+DFS）

给你无向 连通 图中一个节点的引用，请你返回该图的 深拷贝（克隆）。

图中的每个节点都包含它的值 val（int） 和其邻居的列表（list[Node]）。

class Node {
    public int val;
    public List<Node> neighbors;
}
 

测试用例格式：

简单起见，每个节点的值都和它的索引相同。例如，第一个节点值为 1（val = 1），第二个节点值为 2（val = 2），以此类推。该图在测试用例中使用邻接列表表示。

邻接列表 是用于表示有限图的无序列表的集合。每个列表都描述了图中节点的邻居集。

给定节点将始终是图中的第一个节点（值为 1）。你必须将 给定节点的拷贝 作为对克隆图的引用返回。

示例 1：

输入：adjList = [[2,4],[1,3],[2,4],[1,3]]
输出：[[2,4],[1,3],[2,4],[1,3]]
解释：
图中有 4 个节点。
节点 1 的值是 1，它有两个邻居：节点 2 和 4 。
节点 2 的值是 2，它有两个邻居：节点 1 和 3 。
节点 3 的值是 3，它有两个邻居：节点 2 和 4 。
节点 4 的值是 4，它有两个邻居：节点 1 和 3 。

示例 2：

输入：adjList = [[]]
输出：[[]]
解释：输入包含一个空列表。该图仅仅只有一个值为 1 的节点，它没有任何邻居。

示例 3：

输入：adjList = []
输出：[]
解释：这个图是空的，它不含任何节点。
**```
示例 4：**
![在这里插入图片描述](https://img-blog.csdnimg.cn/20210408152447324.png)

```cpp
输入：adjList = [[2],[1]]
输出：[[2],[1]]

提示：

1.节点数不超过 100 。
2.每个节点值 Node.val 都是唯一的，1 <= Node.val <= 100。
3.无向图是一个简单图，这意味着图中没有重复的边，也没有自环。
4.由于图是无向的，如果节点 p 是节点 q 的邻居，那么节点 q 也必须是节点 p 的邻居。
5.图是连通图，你可以从给定节点访问到所有节点。

算法分析：

1. 复制所有点，并且能从原来的点找到复制后的点。
2. 复制所有边。

遍历图一遍就能把所有点遍历出来了，然后存一下从原来图上的点到创建出的复制点的映射（用一个哈希表来维护），如果原图上A->B有边，那么就在对应的新图的结点A’和B’之间连接边。

注意是无向图，所以边要双向连接，不过这里只要在遍历每个点的时候连“从它到的边”这样就自然而然的把原来的所有双向边都复制了。

(DFS) O(n)
递归地访问(复制)邻居节点，用一个map来存储节点访问情况

算法分析

• 1、复制所有的点
  用哈希表存储 原来的点 -> 复制后的点，通过dfs找到所有的点，并把该点进行复制，存入哈希表中
• 2、复制所有的边
  枚举整个哈希表，key表示原来的点，value表示复制后的点，枚举key所有的邻接点，并找到邻接点对应的哈希表中映射点（即邻接点的复制点），新开一个链表，把所有的邻接点的复制点都加入该链表中，并把链表赋值到value.neighbors中。

代码：

/*
// Definition for a Node.
class Node {
public:
    int val;
    vector<Node*> neighbors;
    Node() {
        val = 0;
        neighbors = vector<Node*>();
    }
    Node(int _val) {
        val = _val;
        neighbors = vector<Node*>();
    }
    Node(int _val, vector<Node*> _neighbors) {
        val = _val;
        neighbors = _neighbors;
    }
};
*/

class Solution {
public:
    unordered_map<Node*,Node*> hash;  //哈希表存储：原来的点 -> 复制后的点

    Node* cloneGraph(Node* node) {
        if(!node) return NULL;  //如果节点为空，直接返回空。
        //dfs完成对所有点的复制
        dfs(node);  //从node节点开始深搜
        //dfs结束就完成了对所有点的复制
        //下面完成对所有边的复制
        for(auto [s,d]:hash){   //通过枚举原图上点(s)的边，完成新图上(d)点之间边的复制，
            for(auto e:s->neighbors){  //再枚举一下原图上所有点的临边
                //如果原图上有A到B的边，则这里我们就需要完成复制从A的小弟A'到B的小弟B'的边。
                d->neighbors.push_back(hash[e]);    //即把原图上的点e对应的新点hash[e]放到d对应的临边数组上(看定义结构)

            }
        }
        return hash[node];  //最后我们返回node节点对应的的新图是上的点。
    }

    void dfs(Node* node){
    	//对于该点，复制一个新点
        hash[node]=new Node(node->val); //先复制一下当前点，存储到哈希表中
        //遍历该点的邻点，即在dfs的过程中完成对这些节点的复制
        for(auto e:node->neighbors){    //再遍历一下node节点的所有临边上的节点，把它们也复制一下存储到哈希表中
            if(hash.count(e)==0){   //只要在哈希表中还没有存储过这个节点，我们就需要对这个点e进行深搜
                dfs(e); //继续深搜这个点
            }
        }
    }
};

java代码：（学会java中哈希表如何同时枚举key和value）

且注意java的邻居节点是用数组列表实现的。

class Solution {
    static HashMap<Node,Node> map=new HashMap<Node,Node>();
    static void dfs(Node node){
        map.put(node,new Node(node.val));
        for(int i=0;i<node.neighbors.size();i++){
            Node t=node.neighbors.get(i);
            if(!map.containsKey(t)){
                dfs(t);
            }
        }
    }
    public Node cloneGraph(Node node) {
        if(node==null) return null;
        map.clear();
        dfs(node);
        for(Map.Entry<Node,Node> entry : map.entrySet()) {
            Node a = entry.getKey();
            Node b = entry.getValue();

            List<Node> res = new ArrayList<Node>();
            for(int i = 0;i < a.neighbors.size();i ++)
                res.add(map.get(a.neighbors.get(i)));

            b.neighbors = res;
        }
        return map.get(node);
    }
}

注意也可以在dfs的过程中完成对边的复制：
c++代码：

class Solution {
public:
    //key是原节点，值是克隆节点
    unordered_map<Node*, Node*> hash;
    Node* cloneGraph(Node* node) {
        if(!node) return NULL;
        //克隆一个图时，节点要新建，邻居也要新建，不能把邻居列表简单复制
        hash[node] = new Node(node->val);
        dfs(node);
        return hash[node];
    }
    void dfs(Node* node){
        for(auto x : node->neighbors){
            if(hash.find(x) == hash.end()){
                hash[x] = new Node(x->val);
                dfs(x);
            }
            hash[node]->neighbors.push_back(hash[x]);
        }
    }
};

java:

class Solution {
    Map<Node,Node> map = new HashMap<>();
    public Node cloneGraph(Node node) {
        if(node == null) return null;
        return dfs(node);
    }

    Node dfs(Node node){
        if(map.containsKey(node)) return map.get(node);
        Node clone = new Node(node.val);
        map.put(node,clone);
        for(Node ver: node.neighbors){
            clone.neighbors.add(dfs(ver));
        }
        return clone;
    }
}

2021年10月8日21:52:57:

/*
// Definition for a Node.
class Node {
    public int val;
    public List<Node> neighbors;
    public Node() {
        val = 0;
        neighbors = new ArrayList<Node>();
    }
    public Node(int _val) {
        val = _val;
        neighbors = new ArrayList<Node>();
    }
    public Node(int _val, ArrayList<Node> _neighbors) {
        val = _val;
        neighbors = _neighbors;
    }
}
*/
//深度拷贝即是分为两步，1是复制所有的点，2是复制所有的边，我们给每一个节点开一个小弟节点，我们这里需要开一个哈希表的映射，即存储每一个节点所复制的点，即存储点和其小弟节点
//我们使用深搜来遍历图，深搜不需要开队列
class Solution {
    Map<Node,Node> map=new HashMap<>(); //哈希表map存储所有的点到其小弟节点的映射
    public Node cloneGraph(Node node) {
        if(node==null) return null; //特判空的情况，
        dfs(node);  //否则的话，我们就从根节点开始递归深搜,dfs结束之后，我们就复制完了所有的点

        //第二步是复制所有的边，即我们要遍历原来的所有边，而遍历原来的所有边就是遍历原来的所有的点，而原来的所有的点，都已经被我们存到了哈希表中，所以我们要遍历哈希表
        for(Node n:map.keySet()){ //遍历哈希表，这样n就是原来的所有点           
            Node newn=map.get(n);   //节点newn是n的小弟节点
            for(Node m:n.neighbors){  //枚举n所能到达的所有的相邻节点m,比如说原来有一条从n到m的边，此时我们就要复制一条从n的小弟到m的小弟的边              
                Node newm=map.get(m); //newm就是节点m的小弟节点，此时我们就需要从n的小弟节点newn往m的小弟节点newm连一条边
                newn.neighbors.add(map.get(m)); //即从n的小弟节点往m的小弟节点连一条边
            }
        }
        return map.get(node);   //最后返回节点node的小弟节点，即深拷贝的图的根节点
    }
    public void dfs(Node node){
        Node newNode=new Node(node.val);  //先创建出来node节点的小弟节点
        map.put(node,newNode);  //给node节点复制一个新的点，即在哈希表中存储node和其小弟节点
        for(Node n:node.neighbors){ //之后再遍历node节点的所有邻边，即往node节点的所有相邻节点进行递归
            if(!map.containsKey(n)){  //注意不要重复遍历，只有当哈希表中没有这个节点的时候，我们才要递归搜索这个点
                dfs(n); //哈希表中没有n这个节点，我们就递归搜索n这个节点
            }
        }
    }
}

2021年10月29日14:06:44：

/*
// Definition for a Node.
class Node {
    public int val;
    public List<Node> neighbors;
    public Node() {
        val = 0;
        neighbors = new ArrayList<Node>();
    }
    public Node(int _val) {
        val = _val;
        neighbors = new ArrayList<Node>();
    }
    public Node(int _val, ArrayList<Node> _neighbors) {
        val = _val;
        neighbors = _neighbors;
    }
}
*/

//这个题目首先是无向图,所以我们在存边的时候,假如a,b之间有一条边,则我们就既需要存储a到b的边,也需要存储b到a的边,
//其次图是连通图,即我们任意从图中的一个点出发都可以遍历完整张图; 我们在复制图的时候需要把所有的点和边都需要复制
//重点是代码不知道怎么写,首先是复制所有的点,我们需要遍历整张图,可以使用dfs，同时为了避免重复搜索，我们需要判重；这里在判重的时候即是在哈希表中还没有这个点
//我们还需要根据原来的点找到其克隆的小弟节点，所以我们需要存储原点和小弟节点的映射，
//我们在dfs的过程中完成对所有点的复制，即为每一个点复制一个小弟节点，之后我们再枚举所有的点(从哈希表中)，为每一个点复制其边，时间O(n+m),n节点个数，m是边数

class Solution {
    Map<Node,Node> map=new HashMap<>(); //哈希表存储原点和其小弟节点的映射

    public Node cloneGraph(Node node) {
        if(node==null) return null; //判空
        dfs(node);  //从node节点开始深搜，因为图是无向连通图，所以任意从一个点重复都可以访问到图中所有的点
        //经过上面的dfs的操作就可以把所有点复制一遍了

        //之后我们就需要复制所有边，复制原来的所有边的话，我们就需要遍历一下原来的点的所有边，我们此时已经把所有点都存储到了哈希表中了
        //所以我们就可以遍历哈希表中的所有的点了
        for(Node n:map.keySet()){   //这里n就是原来的所有的点n
            Node newN=map.get(n);   //newN就是节点n的小弟节点
            //再枚举节点n的边，假设从a到b有一条边，我们就需要从a的小弟往b的小弟连一条边了
            for(Node m:n.neighbors){  //枚举节点n的所有相邻节点m
                Node newM=map.get(m); //从哈希表中取出节点m的小弟节点newM
                newN.neighbors.add(newM);   //这一步操作即是往n的小弟节点往m的小弟节点连一条边  
            }
        }
        return map.get(node);   //随便返回新图的一个节点即可
    }

    public void dfs(Node node){
        Node newNode=new Node(node.val);  //先为每一个节点创建一个小弟节点
        map.put(node,newNode);  //再存储下来原点和小弟节点的映射
        for(Node n:node.neighbors){ //再使用dfs的经典for循环的写法遍历node节点的所有相邻节点
            //在遍历这个点之前要保证这个点没有被遍历过，即在哈希表中还没有存储这个点
            if(!map.containsKey(n)){
                dfs(n); //这样我们就可以遍历这个点，即是继续从这个点开始往下递归遍历，这样就可以把所有点全部复制一遍
            }
        }
    }
}

211. 添加与搜索单词 - 数据结构设计(trie树+dfs）

请你设计一个数据结构，支持 添加新单词 和 查找字符串是否与任何先前添加的字符串匹配 。

实现词典类 WordDictionary ：

• WordDictionary() 初始化词典对象
• void addWord(word) 将 word 添加到数据结构中，之后可以对它进行匹配
• bool search(word) 如果数据结构中存在字符串与 word 匹配，则返回 true ；否则，返回 false 。word 中可能包含一些 '.' ，每个 . 都可以表示任何一个字母。

示例：

输入：
["WordDictionary","addWord","addWord","addWord","search","search","search","search"]
[[],["bad"],["dad"],["mad"],["pad"],["bad"],[".ad"],["b.."]]
输出：
[null,null,null,null,false,true,true,true]

解释：
WordDictionary wordDictionary = new WordDictionary();
wordDictionary.addWord("bad");
wordDictionary.addWord("dad");
wordDictionary.addWord("mad");
wordDictionary.search("pad"); // return False
wordDictionary.search("bad"); // return True
wordDictionary.search(".ad"); // return True
wordDictionary.search("b.."); // return True

提示：

1 <= word.length <= 500
addWord 中的 word 由小写英文字母组成
search 中的 word 由 '.' 或小写英文字母组成
最多调用 50000 次 addWord 和 search

算法分析：
(trie树) add:O(L),search:O(nL)
我们可以用trie树来保存所有单词。
trie树也叫字典树，如下所示，该树中存储了
"at", "bee", "ben", "bt", "q"这几个单词。

因为插入的单词不包含通配符.，所以我们可以直接插入。
难点在于如何查找包含通配符的单词。我们可以用DFS搜索：

1. 当遇到字母a-z时，直接进入trie树节点对应的儿子；
2. 当遇到通配符.时，枚举当前trie树节点的所有儿子；

时间复杂度分析：假设单词的平均长度是 L，总共有 n 个单词。add操作会遍历 L 个节点，所以时间复杂度是 O(L) ；search操作最坏情况下会遍历所有节点，所以时间复杂度是 O(nL)。

代码：

class WordDictionary {
public:
    //下面和208实现trie树基本上完全一样。
    struct node{
        bool is;
        node* son[26];  //定义26个孩子节点
        //构造函数
        node(){
            is=false;
            for(int i=0;i<26;i++){  //将26个儿子进行初始化
                son[i]=NULL;
            }
        }
    }*root; //定义一个根节点
    /** Initialize your data structure here. */
    WordDictionary() {
        root=new node();    //初始化根节点
    }
    
    void addWord(string word) { //实现插入一个单词
        auto p=root;
        for(auto c:word){
            int u=c-'a';
            if(!p->son[u]) p->son[u]=new node();
            p=p->son[u];
        }
        p->is=true; //最后注意记得标记这个单词
    }
    
    bool search(string word) {  //实现搜索一个单词
        return dfs(root,word,0);    //写一个爆搜，返回一个爆搜的结果，第一个参数表示从根节点开始搜，
        //第二个参数表示搜索的是word这个单词，第三个参数表示从下标0开始搜索
    }

	//下面开始编写dfs函数。
    bool dfs(node* p,string word,int i){
        if(i==word.size()) return p->is; //如果我们已经遍历完了最后一个单词，说明我们已经遍历完这个单词，我们最后只需要看一下最后这个位置是否已经被标记即可
        //否则就说明还没有遍历完这个单词，我们就需要继续正常的搜索即可
        // 当遇到字母 a - z 时，直接进入 trie 树节点对应的儿子
        if(word[i]!='.'){   //如果当前位置不是'.',那我们就正常的看一下这个位置上是否有单词即可
            int u=word[i]-'a';
            if(!p->son[u]) return false; //如果这个位置上不存在单词直接返回false
            return dfs(p->son[u],word,i+1); //否则的话我们就从这个孩子节点开始继续往下一个位置搜索
            
        }// 当遇到通配符 . 时，枚举当前 trie 树节点的所有儿子
        else{  //否则就说明当前位置是一个点，我们就需要枚举这个节点的所有孩子节点
            for(int j=0;j<26;j++){  //枚举一下每一个分支
                if(p->son[j]&&dfs(p->son[j],word,i+1)) return true; //如果存在这个分支并且这个分支可以搜到的话，我们就返回true,
            }
            return false;   //如果上面分支都没有搜到的话，就返回false
        }
    }
};

212. 单词搜索 II （DFS+Trie树优化）

给定一个 m x n 二维字符网格 board 和一个单词（字符串）列表 words，找出所有同时在二维网格和字典中出现的单词。

单词必须按照字母顺序，通过 相邻的单元格 内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母在一个单词中不允许被重复使用。

示例 1：

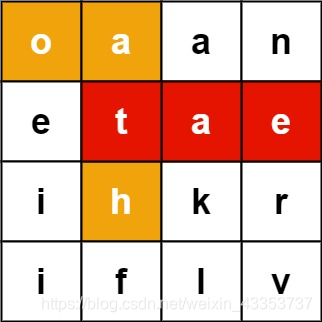
输入：board = [["o","a","a","n"],["e","t","a","e"],["i","h","k","r"],["i","f","l","v"]], words = ["oath","pea","eat","rain"]
输出：["eat","oath"]

示例 2：

输入：board = [["a","b"],["c","d"]], words = ["abcb"]
输出：[]

提示：

m == board.length
n == board[i].length
1 <= m, n <= 12
board[i][j] 是一个小写英文字母
1 <= words.length <= 3 * 104
1 <= words[i].length <= 10
words[i] 由小写英文字母组成
words 中的所有字符串互不相同

算法分析：
dfs+trie树。

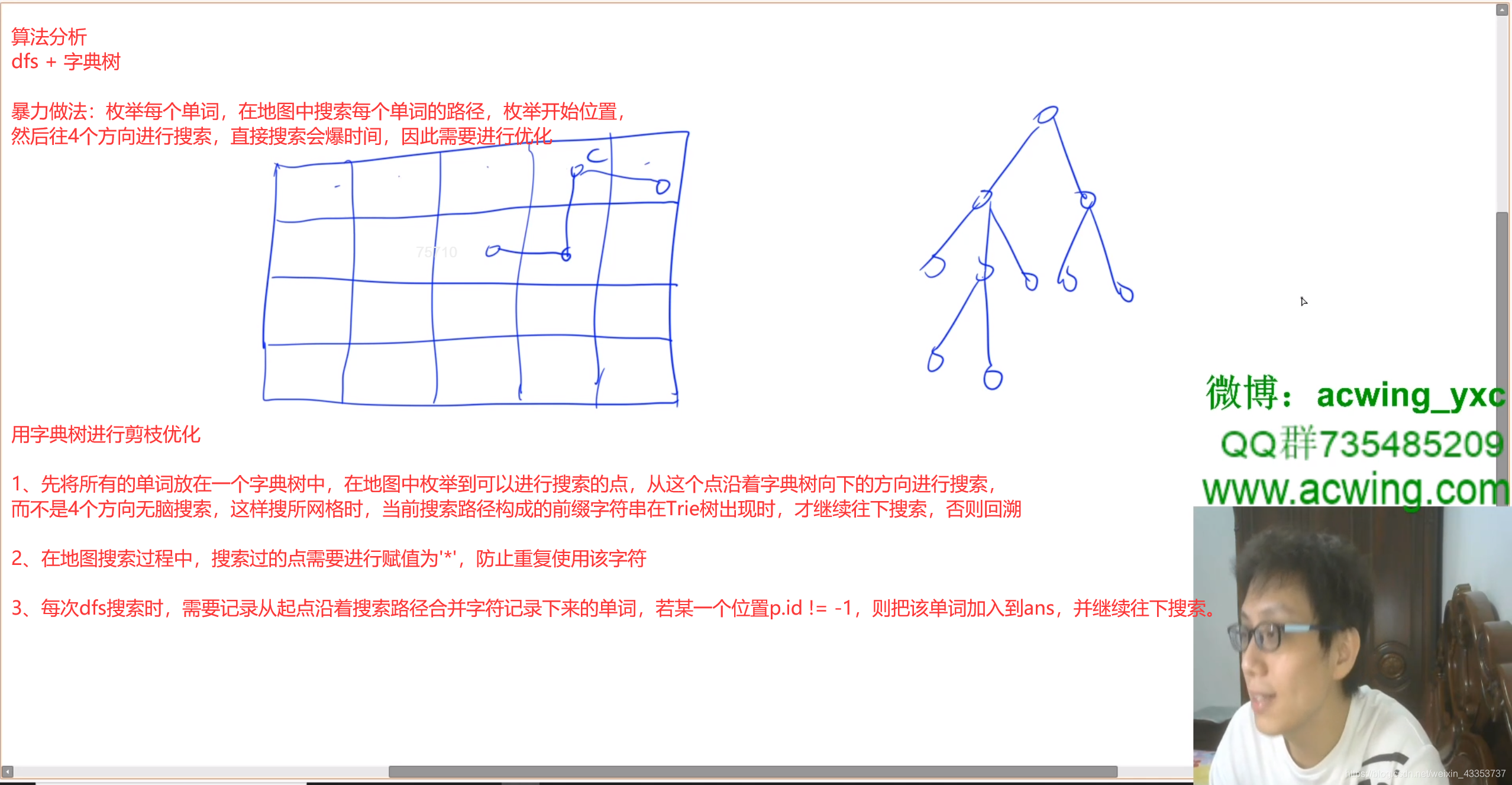
代码：

class Solution {
public:
    struct node{
        //由于我们要知道当前是哪个单词，最后我们要把遍历到的单词都输出出来，所以这里我们就不能再存储结尾了，而是要存储编号
        int id;// 单词在words单词列表中的下标，-1表示不存在以这个结点结尾的单词
        node* son[26];
        //构造函数
        node(){
            id=-1;  //-1表示当前位置是空的
            for(int i=0;i<26;i++) son[i]=NULL;  //每个孩子初始化为空

        }
    }*root; //定义一个根节点
    vector<vector<char>> g; //由于下面我们需要编写爆搜函数，需要用到二维数组，我们要把二维数组定义为全局变量，就可以少传一个参数，否则传来传去太麻烦了
    int dx[4]={-1,0,1,0},dy[4]={0,1,0,-1};  //定义方向矩阵
    unordered_set<int> ids; //开一个哈希表存储答案的单词的id集合，由于可能会有重复的，所以这里我们用的是set

    //实现insert函数，即是在Trie树中插入单词
    void insert(string& word,int id){   //word是单词列表中的单词，id是这个单词在单词列表中的下标
        auto p=root;
        for(auto c:word){
            int u=c-'a';
            if(!p->son[u]) p->son[u]=new node();
            p=p->son[u];
        }
        // 记录单词的id
        p->id=id;   //以当前单词结尾的单词id是id
    }

    vector<string> res; //数组res存放最终答案，即是同时存在于单词列表和二维网格中的单词

    vector<string> findWords(vector<vector<char>>& board, vector<string>& words) {
        g=board;
        root=new node();   //初始化根节点
        for(int i=0;i<words.size();i++) insert(words[i],i); //把单词列表中的每一个单词均插入到单词列表中，i是这个单词在单词列表words里的下标
        // 遍历所有可能的起点做dfs
        for(int i=0;i<g.size();i++){  //让二维网格中的每一个字母均作为起点枚举一下
            for(int j=0;j<g[i].size();j++){
                int u=g[i][j]-'a';  //将字母a~z映射到0~25
                // 检查是否可以作为起点
                if(root->son[u]) {  //如果这个点存在的话，我们就继续往下面递归搜索。
                    dfs(i,j,root->son[u]);  //从(i,j)这个点，从root->son[u]这个节点继续往下递归搜索
                }

            }
        }
        //结束递归，我们看一下一共遍历到了几个单词，将这些单词存放到res里面
        for(auto id:ids) res.push_back(words[id]);
        return res; //最后返回答案
    }

    //下面编写dfs函数
    void dfs(int x,int y,node* p){  //传入参数包括这个点的横纵坐标和当前节点
        //每层递归遍历的时候，只要发现找到了一组答案，我们就要把这个答案放到答案哈希表中(set可以起到去重的作用，所以不会把同一个单词放多次)。
        if(p->id!=-1) ids.insert(p->id); //如果当前节点的id!=-1，说明存在一个单词以这个节点结尾，我们就需要把这个节点加到答案里面(因为我们可能会搜到重复的单词，所以这里我们使用哈希表set去重)
        // 记录这个地方搜索过了(下面还需要回溯，所以这里我们需要先记录下来当前字符g[x][y])
        char t=g[x][y]; //在标记当前字符之前，先记录下来当前字符
        //将当前字符标记一下
        g[x][y]='*';    //将当前字符标记为一个不存在的字符，后面递归的时候代表这个位置已经被搜索过了，之后我们不能再搜索这个位置了
        // 向四个方向搜索
        for(int i=0;i<4;i++){
            int a=x+dx[i],b=y+dy[i];  //求出下个我们将要递归的方向的坐标(a,b)
            if(a>=0&&a<g.size()&&b>=0&&b<g[0].size()&&g[a][b]!='*'){   //如果a,b均没有越界且这个节点没有被搜索使用过，我们就可以继续往下遍历这个点
                int u=g[a][b]-'a';  
                if(p->son[u]) dfs(a,b,p->son[u]);  //如果在trie树中存在这个节点，我们就继续往下搜索这个节点
            }
        }
        // 恢复现场
        g[x][y]=t;
    }
};

2021年9月1日16:02:55：

216. 组合总和 III

找出所有相加之和为 n 的 k 个数的组合。组合中只允许含有 1 - 9 的正整数，并且每种组合中不存在重复的数字。

说明：

• 所有数字都是正整数。
• 解集不能包含重复的组合。

示例 1:

输入: k = 3, n = 7
输出: [[1,2,4]]

示例 2:

输入: k = 3, n = 9
输出: [[1,2,6], [1,3,5], [2,3,4]]

依次枚举每个位置填什么数字, 组合类题目, 属于模版题

代码：

class Solution {
public:
    vector<vector<int>> res;  //定义答案数组
    vector<int> path;   //定义方案数组
    vector<vector<int>> combinationSum3(int k, int n) {
        dfs(1,n,k);    //从1开始递归，n为选的数之和，k为选的数的个数，n,k一开始就是题目给出的n,k
        return res;    //最后递归结束，返回最终答案
    }
    void dfs(int start,int n,int k){    //start表示本次递归的开始数，n为我们已经选的数之和，k为我们已经选的数的个数，
    //注意我们每选择一个数是让n减去其值，让k减一即个数减一
        if(n==0&&k==0){  //如果n被减的变成了0，k被减的变成了0，就把当前方案放到答案数组里
            res.push_back(path);       
        }else if(n!=0&&k!=0){   //如果n,k都不为0，说明递归还没有结束，我们就执行递归
            for(int i=start;i<=9;i++){  //从递归位置一直枚举到9
                if(n>=i){   //枚举的时候也要看是否合法，即我们准备加的数不能超过剩下的n，一定不要忘了写。也可以吧这一句放到for循环里面。
                	//下面和39,40是不同的，我们先把i加到答案数组里，再往下递归
                    path.push_back(i);  //i是合法的，就把i加入到答案里，我们此时就是选择了i，所以我们现在需要从i+1开始选
                    dfs(i+1,n-i,k-1);   //这时我们就需要从i+1开始枚举(注意不是u+1,应该是动态值，因为我们可能加入的不止一个数)，此时还可以凑的和是n-i,
                    //还可以凑的数的个数是k-1(不能写成k--,k--是先取k，再减一，明显不对）
                    path.pop_back();    //每次递归回溯都需要恢复现场。！！！非常重要。
                }
            }
    //这里根据if语句还有n==0&&k!=0,和n!=0&&k==0,但是这两种情况都不需要判断，因为都是不合法的方案情况。
        }
    }
};

2021年9月2日11:58:55：

//找出来相加之和为n的k个数的组合,并且组合中只能有1~9之间的正整数,并且每种组合种不能存在相同的数,即比如n=9,k=3,则[1,1,7]或者[3,3,3]是不行的,因为存在相同的1或3
//而[1,2,6]和[1,3,5]是可以的,因为虽然1是重复的,但是不是在同一个组合中,两个1是在不同的组合中,这一点要注意
//这个题目和1~n的全排列还有从n个数中选取k个数,这三个题目当成模板背下来,
//为了避免重复枚举数字,我们人为规定一个顺序：即只能从前往后选,不能从后往前选,即按照123456789的顺序往后选,这样就可以避免出现先选了一个123,又选了一个132的这种重复的方案,
//即保证后一个数一定要比前一个数要大,所以我们需要记录一个start,即当前位置上的数最小可以从哪个数开始搜,即start是从1开始枚举的,还需要记录k和n,k是枚举了几个数了,n是当前总和是多少
//比如说现在start当前是4,我们就从4递归一下,是5就从5递归一下,......,注意这里和之前的很多题目一样,我们每选取一个数就让k减一,让n减去这个数值
//时间复杂度：O(C9, k) *O(k),即是9个数中任意选k个数,再乘以记录方案的时间O(n),
class Solution {
    List<List<Integer>> res=new ArrayList<>();  //res记录答案,即所有解
    List<Integer> path=new ArrayList<>(); //path表示当前解,path是全局的,所以注意回溯操作
    public List<List<Integer>> combinationSum3(int k, int n) {
        dfs(1,k,n); //start从第一个开始搜索,k是当前还需要选取几个数,n是还需要选取的总和是多少
        return res; //递归结束之后,将答案数组返回
    }
    public void dfs(int start,int k,int n){
        if(n==0){ //我们每凑一个1个数,就让k减一,让n减去对应数值,这样当n减到0并且k也变成了0,就说明我们找到了一个方案
            if(k==0) res.add(new ArrayList<>(path));
        }else{  //否则即和还没有到n
            if(k!=0) {//同时个数还不到k个,我们就需要从数start开始枚举,最大到9
                for(int i=start;i<=9;i++){  //i从start开始枚举,最大到9,之后继续往后递归
                    if(n>=i){ //我们不能直接往下就去递归,我们首先需要保证还需要枚举的n的值大于i,否则就不用再往下枚举了,注意是i,表示start, 因为start可能不合适,我们需要往后枚举即是i,
                        path.add(i);  //如果n>=i,我们就需要选取i,并且要将i加到path中
                        //继续往下递归
                        dfs(i+1,k-1,n-i); //当前需要枚举的数是i+1,需要枚举的数还有k-1个,还需要枚举的总和是n-i
                        //记得回溯即需要恢复现场
                        path.remove(path.size()-1);
                    }
                }
            }//else{  //否则就是说和还没有到n但是k已经枚举够了,即是不合法的情况,我们可以不用写这个else了
            //}
        }
    }
}

2021年10月22日21:32:58：

class Solution {

//这个题目是让我们用[1~9]中的k个数组合出来所有相加为n的组合,一个组合中不能使用同一个数字,即一个组合中每一个数字只能被用一次,并且不能包含重复的组合
//又是找出来所有的方案,所以还是dfs解决,搜索组合和搜索排列两种题目的算法代码是不同的,
//这个题目即是从1,2,3,4,5,6,7,8,9中选数字,我们为了避免重复,我们规定我们只能从前往后选数,这样我们就不会出现有一个组合是[1,2,3],
//而另一个组合是[1,3,2]这种情况了,因为我们必须要保证选数的时候是从前往后选的,而3,2显然不是从前往后选的,
//因此我们在dfs的时候需要记录当前搜索到了数组中的哪一个数start了,start的范围是从1到9,每次搜索的时候从start开始枚举,
//比如现在从4开始搜索,则之后往下递归的时候只能选比4大的数:5,6,7,...
//同之前的题目一样,我们这里传递个数和总和的时候都是使用的减,并且在添加一个数的时候要保证剩下的n是要>=要添加的数i的

    List<List<Integer>> res=new ArrayList<>();
    List<Integer> path=new ArrayList<>();

    public List<List<Integer>> combinationSum3(int k, int n) {
        dfs(1,k,n); //刚开始递归的时候从1开始枚举,当前需要凑的数的个数是k个,当前需要凑的数的总和是n
        return res; //递归结束返回答案数组
    }
    public void dfs(int start,int k,int n){ //在dfs的过程中,完成组合的选取,start是当前枚举到了1~9中的哪个数了,k是当前需要凑的数的个数,n是当前需要凑的总和
        if(n==0){   //我们先来判断元素当前总和n是不是已经被减到0了,
            if(k==0){  //再来看一下是不是正好凑够了k个数,如果也是的话,我们就把当前路径加到res中
                res.add(new ArrayList<>(path));
            }//else,即n是0但是k!=0,这种情况是无解的,我们可写可不写
        }else if(k!=0){ //再否则n!=0,并且k!=0,即和没有凑够并且个数也不够k个,那我们就可以枚举添加数字,即枚举当前位置选什么,还有其他情况,所以这里是else if
            for(int i=start;i<=9;i++){  //当前可以填的数从start开始枚举,最大到9
                //在枚举的时候也要判断一下i是否合法
                if(n-i>=0){ //要保证n是>=i的,否则i就不能选
                    path.add(i);  //满足了if,说明i可以选,我们就选择i加到path中
                    dfs(i+1,k-1,n-i); //之后继续往下递归,继续看下一个数,注意是i+1,不是start+1,k即要凑的数的个数要减一
                    //(注意是k-1,不能是k--,因为k--的话用的k,用完之后再减一,而我们用的就应该是减完之后的k,所以是k-1),n即要凑的总和要减i
                    path.remove(path.size()-1); //递归结束的时候要回溯,即去掉最后添加的元素
                }
            }
        }//再否则n!=0但是k=0的话,就表示个数已经够了,但是总和还没有凑够,这是一种不合法的情况,我们就不用管了,这里的else就可以不用写了
    }
}

更简单一点的：

class Solution {
    List<List<Integer>> res=new ArrayList<>();
    List<Integer> path=new ArrayList<>();

    public List<List<Integer>> combinationSum3(int k, int n) {
        dfs(1,k,n);
        return res;
    }
    public void dfs(int start,int k,int n){
        if(n==0&&k==0){
            res.add(new ArrayList<>(path));
            return;
        }
        if(n==0||k==0) return;
        for(int i=start;i<=9;i++){
            path.add(i);
            dfs(i+1,k-1,n-i);
            path.remove(path.size()-1);
        }
    }
}

377. 组合总和 Ⅳ（dp求方案数）

给你一个由 不同 整数组成的数组 nums ，和一个目标整数 target 。请你从 nums 中找出并返回总和为 target 的元素组合的个数。

题目数据保证答案符合 32 位整数范围。

示例 1：

输入：nums = [1,2,3], target = 4
输出：7
解释：
所有可能的组合为：
(1, 1, 1, 1)
(1, 1, 2)
(1, 2, 1)
(1, 3)
(2, 1, 1)
(2, 2)
(3, 1)
请注意，顺序不同的序列被视作不同的组合。

示例 2：

输入：nums = [9], target = 3
输出：0

提示：

• 1 <= nums.length <= 200
• 1 <= nums[i] <= 1000
• nums 中的所有元素 互不相同
• 1 <= target <= 1000

2021年9月16日18:15:27：

2021年10月23日10:23:29：

class Solution {

//这个题目中的数组中的数字可以用无限次,并且看样例数的顺序不同方案不同,在这个题目中[1,1,2]和[1,2,1]是不同的方案,所以这个题目就和之前的组合数的题目不一样了,
//我们之前的组合总和的问题都是从前往后依次考虑每一个数,这里我们考虑的时候是看每一个位置填哪个数,第一个位置有n种选择,第二个位置也有n种选择,因为每一个数可以用无限次
//第三个位置也有n种选择,...依次类推,所以这个题目按照顺序枚举的时候枚举的是位置,和其他题目是不同的,
//这个题目有点类似于完全背包问题,都是完全背包问题是数的顺序不同都是方案是视为相同的方案,
//因为这个题目求的是组合的总数,而不是具体的所有的方案,所以我们考虑使用dp来解决,
//有点类似于完全背包问题,我们这里用f[i][j]表示前i个位置总和为j的方案数量(而完全背包问题这里是前i个数总和是j的方案数),
//状态计算:即对应着集合划分的过程，我们以最后一个位置即第i个位置是哪一个数哪一个数不同划分成不同的集合，假设最后一个数选的是ak,即第i个位置选的是ak
//则前i-1个位置选的数的总和就是j-ak,这种情况下的方案数是f[i-1][j-a[k]],所以总的f[i][j]就是所有情况数量之和，时间就是O(n^3)
//我们考虑来优化：用f[j]表示所有总和为j的所有方案的数量，我们考虑最后一个数是什么来划分集合，最后一个数可以是a1,a2,...an,比如是ak,则这种情况的方案数就是f[j-ak],
//最后f[j]=上面所有情况的之和，因为ak是<j的，所以当我们先计算出来的j-a[k]是<j的，所以当我们从小到大枚举的时候就可以保证先小的先被计算出来，
//这样时间复杂度就变成了O(n^2)了,注意因为是排列问题(考虑顺序)，所以要先从小到大枚举体积，再枚举数组中的数字，这一点是和普通的完全背包问题是不同的

    //下面就可以仿照优化空间之后的完全背包问题来写代码了，即使用一维空间，之后再从小到大枚举体积
    public int combinationSum4(int[] nums, int m) {
        int n=nums.length;
        int[] f=new int[m+10];  //m是总体积,状态数组f[i]表示所有总和是i的方案的数量
        //状态初始化f[0]=1,表示凑出来和是0的方案数量是1种
        f[0]=1; //状态初始化f[0]=1,这一个状态初始化很重要
        //更新状态数组
//注意这里和普通的背包问题是不同的，普通的背包问题可以视为组合问题，即不考虑顺序(顺序不同视为同一种方案)，但是这里是排列问题，排列强调元素之间的顺序
//这个题目虽然名字叫组合总和，但是和普通的组合问题不同，普通的组合问题是不考虑顺序的，但是这个题目要求考虑顺序，即视为考虑顺序的排列问题
//总结：组合不强调元素之间的顺序，排列强调元素之间的顺序
//如果求组合数就是外层for循环遍历物品，内层for遍历背包(即普通背包问题的枚举方式)，但是如果求排列数就是外层for循环遍历背包，内层for循环遍历物品
//所以下面的代码如果我们先枚举的数组中的数，再枚举体积的话就是错误的，应该先枚举体积再枚举数组中的数，

        for(int j=0;j<=m;j++){  //从小到大枚举体积更新所有的f[i],这里之所以要从小到大枚举体积,因为我们发现我们要更新f[j]的话，
        //f[j]依赖的所有的f[j-a[k]]都是小于j的，所以我们要在计算f[j]之前要把所有小于j的状态都计算出来，所以我们要从小到大枚举j，这样才可以保证计算大的f[j]之前所有的小的f[j-a[k]]都会被计算出来，
              //再枚举所有的数，注意这里一定要先枚举所有体积j,再枚举数组中的每一个数字x来更新f[j]
              for(int x:nums){
                if(j>=x){   //只有当j是>=x的，我们才可以使用更新j-x状态来更新f[j]
                    f[j]+=f[j-x];
                }
            }
        }
        return f[m];  //最后f[m]就是答案
    }
}

282. 给表达式添加运算符

给定一个仅包含数字 0-9 的字符串和一个目标值，在数字之间添加 二元 运算符（不是一元）+、- 或 * ，返回所有能够得到目标值的表达式。

示例 1:

输入: num = "123", target = 6
输出: ["1+2+3", "1*2*3"] 

示例 2:

输入: num = "232", target = 8
输出: ["2*3+2", "2+3*2"]

示例 3:

输入: num = "105", target = 5
输出: ["1*0+5","10-5"]

示例 4:

输入: num = "00", target = 0
输出: ["0+0", "0-0", "0*0"]

示例 5:

输入: num = "3456237490", target = 9191
输出: []

提示：

0 <= num.length <= 10
num 仅含数字

算法分析：

301. 删除无效的括号

给你一个由若干括号和字母组成的字符串 s ，删除最小数量的无效括号，使得输入的字符串有效。

返回所有可能的结果。答案可以按 任意顺序 返回。

示例 1:

输入: "()())()"
输出: ["()()()", "(())()"]

示例 2:

输入: "(a)())()"
输出: ["(a)()()", "(a())()"]

示例 3:

输入: ")("
输出: [""]

提示：

1 <= s.length <= 25
s 由小写英文字母以及括号 '(' 和 ')' 组成
s 中至多含 20 个括号

306. 累加数 (高精度加法）

累加数是一个字符串，组成它的数字可以形成累加序列。

一个有效的累加序列必须至少包含 3 个数。除了最开始的两个数以外，字符串中的其他数都等于它之前两个数相加的和（即是可以组成一个斐波那契数列）。

给定一个只包含数字 '0'-'9' 的字符串，编写一个算法来判断给定输入是否是累加数。

说明: 累加序列里的数不会以 0 开头，所以不会出现 1, 2, 03 或者 1, 02, 3 的情况。

示例 1:

输入: "112358"
输出: true 
解释: 累加序列为: 1, 1, 2, 3, 5, 8 。1 + 1 = 2, 1 + 2 = 3, 2 + 3 = 5, 3 + 5 = 8

示例 2:

输入: "199100199"
输出: true 
解释: 累加序列为: 1, 99, 100, 199。1 + 99 = 100, 99 + 100 = 199

进阶:
你如何处理一个溢出的过大的整数输入?

答：用数组反过来存储这个整数。

算法分析：
(暴力枚举，高精度加法) O(n^3)
首先枚举开头两个数，然后根据题意每次做高精度加法逐一向后判断。
时间复杂度
枚举开头两个数的时间需要 O(n²)，累加高精度加法验证只需要总共 O(n) 的时间，故总时间复杂度为 O(n³)。
空间复杂度
需要额外 O(n) 的空间存储高精度计算用的数组。

自己枚举前两个数然后判断是不是斐波那契数列。

先枚举第一个数的长度，再枚举一下第二个数的长度，然后用高精度加法算一下两个数的和是多少。以此类推的往后匹配，如果整个这个串都能够匹配完的话，那么这个串就是一个满足要求的串，否则说明当前这种情况是不合法的，往后枚举开头的两个数。

代码：

class Solution {
public:
    //默写高精度加法的模板
    string add(string x,string y){  //注意传入参数和返回值均是string
        // 把两个数(实际上是两个字符串))变成逆序的vector（即倒序存放到数组中）
        vector<int> a,b;
        //把字符转为数字，注意减‘0’
        for(int i=x.size()-1;i>=0;i--) a.push_back(x[i]-'0');   //将字符串x倒序存放到数组a中，现在个位就在a[0],下面我们计算的时候下标从0到n-1,注意减'0'
        for(int i=y.size()-1;i>=0;i--) b.push_back(y[i]-'0');   //将字符串y倒序存放到数组b中，现在个位就在b[0],下面我们计算的时候下标从0到n-1,注意减'0'
        // 数组c存放答案，下面我们计算答案
        vector<int> c;
        for(int i=0,t=0;i<a.size()||i<b.size()||t!=0;i++){  //只要有一个数没有计算完或者进位还不为0，我们就需要计算,t是进位，一开始初始化为0
            if(i<a.size()) t+=a[i];
            if(i<b.size()) t+=b[i]; 
            c.push_back(t%10);  //把个数(t%10)放到答案数组中
            t/=10;  //将t重新赋值为下一位的进位   
        }
        string z; // 把答案变成字符串返回
        //将答案数组倒序存放到字符串中
        for(int i=c.size()-1;i>=0;i--) z+=to_string(c[i]);
        return z; //返回答案
    }
    bool isAdditiveNumber(string num) {
        int n=num.size();   //求出字符串长度
        // 先枚举第一个数的结尾位置
        for(int i=0;i<n;i++){   //枚举一下第一段的结尾位置
            // 再枚举第二个数的结尾位置，由于要保证串中至少要有三个数，所以j + 1 < nums.size()
            for(int j=i+1;j+1<n;j++){ //枚举一下第二段的结尾位置，之所以让j+1<n,是为了给第三个数留下位置
                // 判断一下当前这种情况合法不合法
                // a表示第一个数的起始位置之前的一个位置，b表示第一个数的结束位置,b+1表示第二个数的起始位置，c表示第二个数的结束位置
                //所以第一个数是：a+1~b（长度是b-a）,第二个数是：b+1~c(长度是c-b),c+1是第三个数的起始位置
                int a=-1,b=i,c=j;
                while(true){  //循环里是有break或者return语句提前结束循环的
                    // 先判断一下有没有前导0，如果两个数在计算过程中有一个出现前导0那么都是不合法的
                    if(b-a>1&&num[a+1]=='0'||c-b>1&&num[b+1]=='0') break;   //有前导0，就说明当前情况不合法，我们提前结束本次循环
                    // x表示第一个数
                    auto x=num.substr(a+1,b-a);
                    //y表示第二个数
                    auto y=num.substr(b+1,c-b);
                    //z表示第三个数 执行高精度加法
                    auto z=add(x,y);
                    // 判断一下z是不是和从c+1开始的一段是匹配的，如果不匹配就说明选的不对,也结束本次while循环
                    if(num.substr(c+1,z.size()) != z) break; //和下一个数不匹配
                    // 执行到这里就说明匹配了，我们就需要继续往后看，我们需要更新一下a,b,c三个游标的位置
                    a=b,b=c,c+=z.size();    //把a放到b的位置，之后再把b放到c的位置，把c放到z的最后一个位置（注意要先更新a，之后更新b,最后更新c,搞反了就错了）
                    // 如果恰好匹配完了最后一个位置，说明找到了一个解,只要找到一个解就返回true
                    if(c+1==num.size()) return true;
                }
            }    
        }
        return false;  //如果上面的循环全部执行完还没有返回true,说明就不存在解，我们返回false。
    }
};

java代码：

class Solution {
    public  String add(String x,String y){
        int n=x.length(),m=y.length();
        int[] a=new int[n];
        int[] b=new int[m];
        List<Integer> c=new ArrayList<>();
        for(int i=n-1;i>=0;i--) a[n-i-1]=x.charAt(i)-'0';
        for(int i=m-1;i>=0;i--) b[m-i-1]=y.charAt(i)-'0';
        for(int i=0,t=0;i<n||i<m||t!=0;i++){
            if(i<n) t+=a[i];
            if(i<m) t+=b[i];
            c.add(t%10);
            t/=10;
        }
        String z="";
        for(int i=c.size()-1;i>=0;i--) z+=c.get(i);
        return z;
    }
    public boolean isAdditiveNumber(String s) {
        char[] sc=s.toCharArray();
        int n=s.length();
        for(int i=0;i<n;i++){
            for(int j=i+1;j+1<n;j++){
                int a=-1,b=i,c=j;
                while(true){
                    if(b-a>1&&sc[a+1]=='0'||c-b>1&&sc[b+1]=='0') break;
                    String x=s.substring(a+1,b+1),y=s.substring(b+1,c+1);	
                    String z=add(x,y);
                    //注意java的substring最大为str.size(),不能越界。
                    if(c+z.length()+1>n|| s.substring(c+1,c+z.length()+1).equals(z)!=true) break;	
                    a=b;b=c;c+=z.length();
                    if(c+1==n) return true;
                }
            }
        }
        return false;
    }
}

386. 字典序排数(模拟遍历Trie树）

给你一个整数 n ，按字典序返回范围 [1, n] 内所有整数。
你必须设计一个时间复杂度为 O(n) 且使用 O(1) 额外空间的算法。

示例 1：

输入：n = 13
输出：[1,10,11,12,13,2,3,4,5,6,7,8,9]

示例 2：

输入：n = 2
输出：[1,2]
 

提示：

1 <= n <= 5 * 10^4

2021年10月29日13:06:02：
暴力解：
class Solution {

//暴力：将1~n转化为String数组,然后再按照String大小进行从小到大排序，每一个数的长度约为logn,排序的时间是nlogn,所以总的时间就是
//使用trie树来优化，

    public List<Integer> lexicalOrder(int n) {
        String[] s=new String[n];
        for(int i=1;i<=n;i++) s[i-1]=i+"";
        Arrays.sort(s,(a,b)->{
            return a.compareTo(b);
        });
        List<Integer> res=new ArrayList<>();
        for(int i=0;i<n;i++){
            res.add(Integer.valueOf(s[i]));
        }
        return res;
    }
}

trie树：
class Solution {

//暴力：将1~n转化为String数组,然后再按照String大小进行从小到大排序,每一个数的长度约为logn,排序的时间是nlogn,所以总的时间就是
//使用模拟trie树来优化,将数字看成是字符串插到Trie树中,想象将1~n插到trie数中,我们为了保证字典序,我们从小到大搜索每一个分支,即先搜1,再搜2,再搜3,...
//以1为根节点的子树的所有数一定比以2为根节点的子树的所有数都要小,当我们在搜索的时候搜到的数大于n了,我们就可以停止搜索,因为之后的数一定都是不合法的了
//所以这个题目我们不需要真正的插入，只需要再查询的时候判断一下范围即可，
//使用trie的时间复杂度是O(nlogn),

    List<Integer> res=new ArrayList<>();  //全局答案数组

    public List<Integer> lexicalOrder(int n) {
        for(int i=1;i<=9;i++) { //手动枚举第一位的值
            dfs(i,n); //i是枚举的数字的第一位的值
        }
        return res; //从0开始搜,最大是到n,搜索完毕返回答案数组    
    }

    public void dfs(int cur,int n){ //cur是当前数,n是最大数
        if(cur<=n) res.add(cur);  //当当前数<=n的时候,当前数就是一个合法的数,我们就将cur加到res中
        else return;  //否则当前数一定是>n的,我们就结束递归
        //之后我们在继续看下一位上的数
        for(int i=0;i<=9;i++) { //后面的位上可以是0~9中的任意一个
            dfs(cur*10+i,n);   //使用秦九韶算法求出加上i之后的值再继续往下递归,因为我们的cur是在dfs函数中传递的,所以不需要回溯操作,
        }
    }
}

390. 消除游戏

2022年1月2日11:27:32：

class Solution {

//首先这个题目其实就是和剑指offer上的那个约瑟夫环枪毙问题差不多,都可以是用dp来解决的,
//第一次从左往右从第一个数开始隔一个删一个,隔一个删一个,第二次从右往左从第一个数开始隔一个删一个,第三次和第一次相同,第4次和第2次相同...
//我们用f(n)表示在1~n这n个数中从左往右删除时最后剩余的数,用g(n)表示在1~n这n个数从右往左删除时最后剩余的数
//最后的结果就是f(n),对于f(n),第一次删除之后剩余的数就是2,4,6,8,10,...并且剩余的数的个数就是⌊n/2⌋个，第二次再删就要反过来删除了
//现在我们对剩下的n/2个元素重新编号，我们让其都除以2,即是让2,4,6,8,10,...变成1,2,3,4,5,...⌊n/2⌋,现在我们就要从右往左删除了，
//最后剩下的数即是g(n/2),并且让1,2,3,4,5...⌊n/2⌋变回原序列的时候，最后剩下的数的编号g(n/2)就是2*g(n/2)
//所以f(n)=2*g(n/2),我们现在就需要推出来g(n)的求法,我们这样来考虑:对于1~n,第一次从左往右删如果剩下的编号是f(n)的话
//而如果第一次是从右往左删的话编号是g(n),1,2,3,4,5,...n,我们反过来编号就是n,n-1,n-2,...1,则这样g(n)就是和f(n)是对称的关系，所以g(n)就是和f(n)是中心对称的
//而中心对称的两个位置的两个数的总和就是n+1,比如1和n是对称的总和是n+1,2和n-1是对称的，总和是n+1,...
//所以我们就可以推出来g(n)+f(n)=n+1,又由于f(n)=2g(n/2),所以有：g(n)=n+1-f(n),所以g(n/2)=n/2 +1 -f(n/2),所以f(n)=2(n/2 + 1 -f(n/2))
//所以我们就可以和枪毙问题一样，使用递归解决了，并且每次n会除以2，所以时间就是logn

    public int lastRemaining(int n) {
        if(n==1) return 1;  //特判n=1,并且这也是递归结束的条件
        return 2*(n/2+1-lastRemaining(n/2));  //代入f(n)=2(n/2 + 1 -f(n/2))，这里f就是lastRemaining函数
    }
}

394. 字符串解码

给定一个经过编码的字符串，返回它解码后的字符串。

编码规则为: k[encoded_string]，表示其中方括号内部的 encoded_string 正好重复 k 次。注意 k 保证为正整数。

你可以认为输入字符串总是有效的；输入字符串中没有额外的空格，且输入的方括号总是符合格式要求的。

此外，你可以认为原始数据不包含数字，所有的数字只表示重复的次数 k ，例如不会出现像 3a 或 2[4] 的输入。

示例 1：

输入：s = "3[a]2[bc]"
输出："aaabcbc"

示例 2：

输入：s = "3[a2[c]]"
输出："accaccacc"

示例 3：

输入：s = "2[abc]3[cd]ef"
输出："abcabccdcdcdef"

示例 4：

输入：s = "abc3[cd]xyz"
输出："abccdcdcdxyz"

class Solution {
//dfs即可解决，即递归的解码方式，k[]即表示将[]里面的字符串重复k次，如果[]中还有[]我们就需要递归了，如3[a2[c]]即2[acc]=accacc, 我们从前往后遍历，
//如果我们找到了一个数字k的话，我们就把[  ]中的部分找出来，然后递归的去做，把[ ]里面得到的字符串重复k次就可以了，
    char[] c; //将字符串s转为字符数组，定义为全局的，就可以少传递一个参数
    String s; //因为下面再找字符串中的数字的时候也要用到字符串s，我们也要将字符串s定义为全局的
    int u=0;
    public String decodeString(String _s) {
        c=_s.toCharArray();
        s=_s;
        return dfs();  //直接返回dfs的结果，0表示从字符串s的第0个位置开始搜
    }
    public String dfs(){  //编写dfs函数，u表示当前遍历到了字符串s的哪一位
        String res="";  //定义答案字符串
        while(u<c.length){ //u没有越界, 并且下面有判断右括号的语句，所以这里就没有必要再写判断表示右括号的语句了
            //先找出来当前数字
            if(Character.isDigit(c[u])){
                int k=0;
                while(u<c.length&&Character.isDigit(c[u])){
                    k=k*10+(c[u]-'0');
                    u++;
                }
                String str=dfs();
                while((k--)!=0) res+=str; 
            }else if(Character.isLetter(c[u])){ //当前字符是字母
                res+=c[u++];
            }else if(c[u]=='[') u++; //遍历到左括号直接跳过
            else if(c[u]==']'){
                u++;
                return res; //遍历到右括号说明递归到了最后，我们直接返回当前字符串答案
            }
        }
        return res; //最后将答案字符串返回
    }
}

2021年11月21日21:41:23：

class Solution {

//注意这里是循环嵌套的,即是递归,我们从前往后走,如果遇到一个数字k,就把[ ]里面的形式找出来,再递归的去做[ ]里面的内容,把递归得到的[ ]中的内容再重复k次即可
//注意要把访问字符串的下标u定义为全局的

    char[] c;
    int n;
    int u=0;  //u是访问字符串s的下标,是全局的
    String s;
    public String decodeString(String _s) {
        s=_s;
        c=s.toCharArray();
        n=c.length;
        return dfs();  //dfs的结果就是我们要求的答案字符串
    }

    public String dfs(){
        String res="";  //定义答案字符串
        //从前往后遍历字符串s,直到遍历到']'
        while(u<n&&c[u]!=']'){ //当还没有遍历到']'的时候,我们就要继续遍历字符串s
            if(Character.isLetter(c[u])) res+=c[u++]; //如果当前字符是字母的话,我们就直接把这个字母加到答案字符串中,注意要将下标u加一,即往后走一位
            else if(Character.isDigit(c[u])){ //再判断如果是数字的话,我们就要找出来这个数字,注意数字可能不是一位数,可能是多位数
                int k=u;  //k从u往后找
                while(k<n&&Character.isDigit(c[k])) k++;
                int x=Integer.valueOf(s.substring(u,k));
                u=k+1; //注意我们这里让u=k+1,而不是让u=k,是为了跳过左括号'[',因为每一个数字的后面都是左括号,我们这里是手动跳过左括号'['
                String y=dfs(); //之后我们就需要递归求下面的字符串了,即数字后面的[ ]之间的字符串y
                u++;  //注意递归求解完之后一定要将u++,这里的u++是为了过滤掉']',
                while(x--!=0){
                    res+=y; //将[ ]之间的字符串y重复x次加到答案字符串res的后面
                } 
            }
        }
        return res; //最后返回答案字符串res
    }
}

395. 至少有 K 个重复字符的最长子串

2021年12月17日20:24:28：
好题解

```java
https://leetcode-cn.com/problems/longest-substring-with-at-least-k-repeating-characters/solution/jie-ben-ti-bang-zhu-da-jia-li-jie-di-gui-obla/
2021年12月17日19:53:00：在递归章节
//真的牛皮,使用递归,可以帮助我们深入的理解递归的一个题目,
//递归的重点：我们在调用递归函数的时候,把递归函数当做普通函数(黑箱)来调用,即明白该函数的输入输出是什么,而不用管此函数内部在做什么
//下面是本题的详细讲解,1.递归最基本的就是要记住递归函数的定义:本题的longestSubstring(s,k)函数就是题意,即求一个最长的子字符串的长度,
//并且此字符串中每一个字符的出现次数都至少为k, 函数的参数s是表示原字符串,k是限制条件,即字符串中每个字符的最少出现的次数,函数的返回结果是满足题意的最长字符串的长度
//2.递归的终止条件(即能直接写出的最简单的case):如果字符串s的长度少于k,那么一定不存在满足题意的子字符串,返回0
//3.调用递归(重点)：如果一个字符c在s中出现的次数少于k次，那么s中所有包含c的字符串都不能满足要求，所以，应该在s的所有不包含c的字符串中继续寻找结果:
//即把s按照c进行分割(分割后每一个子串都不包含c(可以使用java中的split函数)),这样就可以得到很多的子字符串t,下面就要求t作为原字符串，求t的最长的满足题意的子字符串的长度
//到目前为止我们已经把大问题分隔为了小问题(s->t),此时我们发现，恰好已经定义了函数longSubstring(s,k)就是来解决这个问题的，所以直接把longSubstring(s,k)函数拿来用,于是就形成了递归
//4.未进入到递归时的返回结果：如果s中的每个字符出现的次数都大于k次，banes就是我们要求的字符串，直接返回该字符串的长度(重要)。
//总之,通过上面的分析，我们看出来了：我们不是为了递归而递归，而是因为我们把大问题拆解成了小问题，恰好有函数可以解决小问题，所以直接用这个函数，由于这个函数正好是本身，所以我们把此现象叫做递归。
//小问题是原因，递归是结果，而递归函数到底怎么一层一层展开与终止的，不要大脑去想，这是计算机要干的事，我们只用把递归函数当做是一个能解决问题的黑箱就够了
//把更多的注意力放在拆解子问题上、递归终止条件、递归函数的正确性上来
//时间复杂度：O(n*26*26),因为函数最多执行26次，for循环遍历一次就是26个字符，循环里面对s的分隔时间复杂度是O(n)
//空间复杂度:O(26*26),函数执行26次，每次开辟26个字符的set空间

class Solution {
    public int longestSubstring(String s, int k) {
        if(s.length()<k) return 0;  //递归结束条件:当字符串的长度都小于k了，说明就算是s字符串都是一个字符，也没有字符满足，所以要返回0
        Map<Character,Integer> map=new HashMap<>(); //哈希表统计每一个字符的出现次数
        for(int i=0;i<s.length();i++) { //遍历计数字符串s中每一个字符的个数
            map.put(s.charAt(i),map.getOrDefault(s.charAt(i),0)+1);
        }
        for(char c:map.keySet()){ //遍历哈希表中每一个字符
            if(map.get(c)<k){ //递归判断条件,如果其个数<k,我们就从字符串s中以其为分隔点进行分隔
                int res=0;  //res统计答案
                for(String t:s.split(c+"")){  //枚举以字符c进行分隔出来的所有子字符串t
                    res=Math.max(res,longestSubstring(t,k));  //使用res更新答案
                }
                return res;
            }
        }
        return s.length();  //最后如果每一个字符的个数都满足>k的话，则答案就是整个字符串的长度，即我们要返回s.length()
    }
}

## 397. 整数替换

给定一个**`正整数 n`** ，你可以做如下操作：

>-  如果 n 是偶数，则用 n / 2替换 n 。 
> - 如果 n 是奇数，则可以用 n + 1或n - 1替换 n 。 
> n 变为 1  所需的最小替换次数是多少？

```java
示例 1：

输入：n = 8
输出：3
解释：8 -> 4 -> 2 -> 1

示例 2：

输入：n = 7
输出：4
解释：7 -> 8 -> 4 -> 2 -> 1
或 7 -> 6 -> 3 -> 2 -> 1

示例 3：

输入：n = 4
输出：2

提示：

1 <= n <= 2^31 - 1

DFS搜索
利用将问题转换成子问题的思想，利用递归很快就能求解。
AC代码：

class Solution {
public:
    typedef long long LL;

    int integerReplacement(int n) {
       return f(n);
    }

    int f(LL n) {
        if (n == 1) return 0;
        if (n % 2 == 0) return f(n / 2) + 1;
        return min(f(n - 1), f(n + 1)) + 1;
    }
};

记忆化搜索优化

记忆化搜索是解决在搜索过程中会遇到搜索重复的子问题，每次对搜索结果进行记录，这样就避免了多余的搜索。

如图：对于每个分支我们原先都会持续搜索下去，直到叶节点，即1

如上图：当我们第一次搜索到18的时候，记录下结果，这样第二次搜索到18的时候就不需要再向下搜索了，直接返回。

记忆化只需要用数组/哈希表来记录搜索的结果，每次搜索前判断是否搜索过，搜索过则直接返回。

2021年8月29日12:33:54：

//我们使用递归，将题目所说的过程模拟出来即可
//时间复杂度是O(根号n)
class Solution {
    Map<Long,Integer> map;	//记忆化搜索的哈希表，记忆n变成1的次数
    public int integerReplacement(int n) {
        map=new HashMap<>(); //记忆化搜索，即备忘录，只要搜索过的我们加到哈希表中，否则重复搜索
        return f(n);
    }
    public int f(long n){
    	//搜索过，我们直接返回
        if(map.containsKey(n)){ //如果已经搜索过n了，就不用再搜索n了，直接从map中取出值即可
            return map.get(n);  
        }
        if(n==1) return 0;  //如果n是1的话，就已经是最终结果了就不需要再做操作了，我们返回0即可，这也是递归的结束条件
        if(n%2==0) {
            map.put(n,1+f(n/2));  //有两个递归函数，别搞混了，这里应该是f，而不是integerReplacement
            return map.get(n);
        }  //否则n就不是1，我们就需要判断一下n是偶数还是奇数，如果是偶数，就用n/2替换n继续做操作，
        //每做一次操作次数加一，所以递归的时候要加一，注意函数是有返回值的，所以这里要写return
        else {  //否则n就是奇数
            map.put(n,1+Math.min(f(n+1),f(n-1)));
            return map.get(n);
             //再否则n就是奇数，我们就使用n+1或者n—1替换n,注意是使得次数最少，所以是去min,注意也要加一
        }
    }
}

433. 最小基因变化（bfs)

2021年10月29日17:34:33：

class Solution {

//和Acwing的845题八数码的问题，即问我们从起点到终点的最短距离，我们使用bfs解决，

    Set<String> set=new HashSet<>();   //set集合存储基因库bank中的所有基因序列
    Map<String,Integer> map=new HashMap<>();  //map存储字符串到起始字符串变化的次数
    Queue<String> q=new LinkedList<>(); //bfs用到的队列
    char[] ch={'A','T','C','G'};  //字符数组ch存储四种不同的字符

    public int minMutation(String start, String end, String[] bank) {
        for(String s:bank) set.add(s);  //将基因库中的所有字符串加到set中
        q.add(start);  //先把start字符串加到队列中
        map.put(start,0);   //start到start的距离是0
        //下面就是bfs的经典套路写法了
        while(q.size()!=0){
            String t=q.poll();
            if(t.equals(end)) return map.get(t);  
            for(int i=0;i<8;i++){  //枚举字符串t的某一位，看其可以变到哪一种状态
                char[] tc=t.toCharArray();  //注意每次都要申请一个新的t字符串对应的字符数组，否则其被别的状态影响
                for(char c:ch){ //枚举ch字符数组的每一个字符
                    tc[i]=c;  //将字符串t的第i位变为c
                    
                    String s=new String(tc);
                    System.out.println(s);
                    if(set.contains(s)&&!map.containsKey(s)){
                        map.put(s,map.get(t)+1);  //用t的距离更新s
                        q.add(s);         
                        if(s.equals(end)) return map.get(s);	//注意因为这里是for循环，所以可能在某一步找到了end,所以我们在这里也要写上判断条件。
                    }
                }
            }
        }
        return -1;
    }
}

473. 火柴拼正方形

2021年12月31日15:18:09：

class Solution {

//这个题目要拼的是正方形,即边数是4,并且每一条边的长度相同,并且要保证所有的火柴都要用到,这个题目使用爆搜加剪枝(不加剪枝无法ac),而我想从这个题目写到如何写爆搜
//先计算数组的总和,只有当总和是4的整数倍的时候才去搜索，否则一定不可以凑出来，
//爆搜,即dfs,搜索顺序:先搜第一条边，看第一边能不能凑出来(边长是sum/4),凑出来之后，我们把所有用过的边打个标记,表示这些边不能再用了，
//再去搜索第二条边，看能否凑出来,能凑出来，就把用过的边打个标记,再去搜索第三条边,第三条也一样，打标记,第四条边就不用再去搜索了，因为我们会先判断sum是不是4的整数倍,到这里之后第四条边一定是可以凑出来的
//剪枝：1.从大到小枚举边,因为我们先用更长的边则剩余的空间就比较小，即可以枚举的可能数量就会更少,即当前这条边可以搜索的深度就可以更短一些,
//2.每条边内部，要求火柴编号递增,因为同样的火柴按照1,3,2的顺序和按照1,2,3的顺序凑出来的边长是一样的,其实这两种方法是等价的,这样我们就可以避免一些重复的情况
//3.如果当前放某根火柴失败了,3.1跳过相同的火柴,3.2如果失败的这根火柴是某条边的第一根火柴,则剪掉当前分支,3.3如果是最后一根,则也要剪掉当前分支

    int[] a;
    boolean[] st;
    int n;  //n是火柴的数量
    public boolean makesquare(int[] _a) {
        a=_a;
        n=a.length;
        st=new boolean[n];
        int sum=0;
        for(int x:a) sum+=x;
        if(sum%4!=0) return false;  //如果总和不是4的整数倍，则一定无解，返回false
        sum/=4; //否则sum除以4,此时sum就是每一条边的边长了
        //第一个剪枝:从大到小枚举边，所以要从大到小排序数组，而java不支持倒排,所以我们就先顺排,再reverse一下即可
        Arrays.sort(a);
        reverse(a,0,n-1);
        return dfs(0,0,sum,0);  
    }

    public boolean dfs(int start,int cur,int length,int cnt){ //第一个参数start是枚举到第几根火柴了,cur是当前的长度,length是要凑出来的单边的总长度,cnt当前拼的是第几根火柴
        if(cnt==3) return true; //如果我们已经拼好了3根火柴(第四根是不用拼的),我们直接返回true
        if(cur==length) return dfs(0,0,length,cnt+1); //否则如果当前拼的长度已经达到length了,我们就继续拼下一根火柴,注意每次都是从第0根开始拼的(不要担心重复，因为我们用st状态数组记录是否已经被用过)
        for(int i=start;i<n;i++){  //从start开始枚举火柴
            if(st[i]) continue; //如果当前火柴已经被用过了，我们就跳过
            if(cur+a[i]<=length){  //如果加上当前火柴之后是不超过length的，我们就加上当前火柴
                st[i]=true; //标记当前火柴已经被用过
                if(dfs(i+1,cur+a[i],length,cnt)) return true;  //继续往下递归，如果说可以找到解，我们就返回true
                st[i]=false;    //回溯，恢复状态
            }
            //下面两条剪枝是上面的第3条(注意不写这两个剪枝，力扣也是可以过的)
            //上面没有返回true,就说明当前根是失败的
            if(cur==0||cur+a[i]==length) return false; //如果是第一根或者最后一根失败，我们就返回false
            while(i+1<n&&a[i+1]==a[i]) i++;   //跳过相同长度的火柴
        }    
        return false;   //如果找不到就返回false
    }

    public void reverse(int[] a,int l,int r){
        while(l<r){
            int t=a[l];
            a[l]=a[r];
            a[r]=t;
            l++;r--;
        }
    }
}

690. 员工的重要性(dfs)

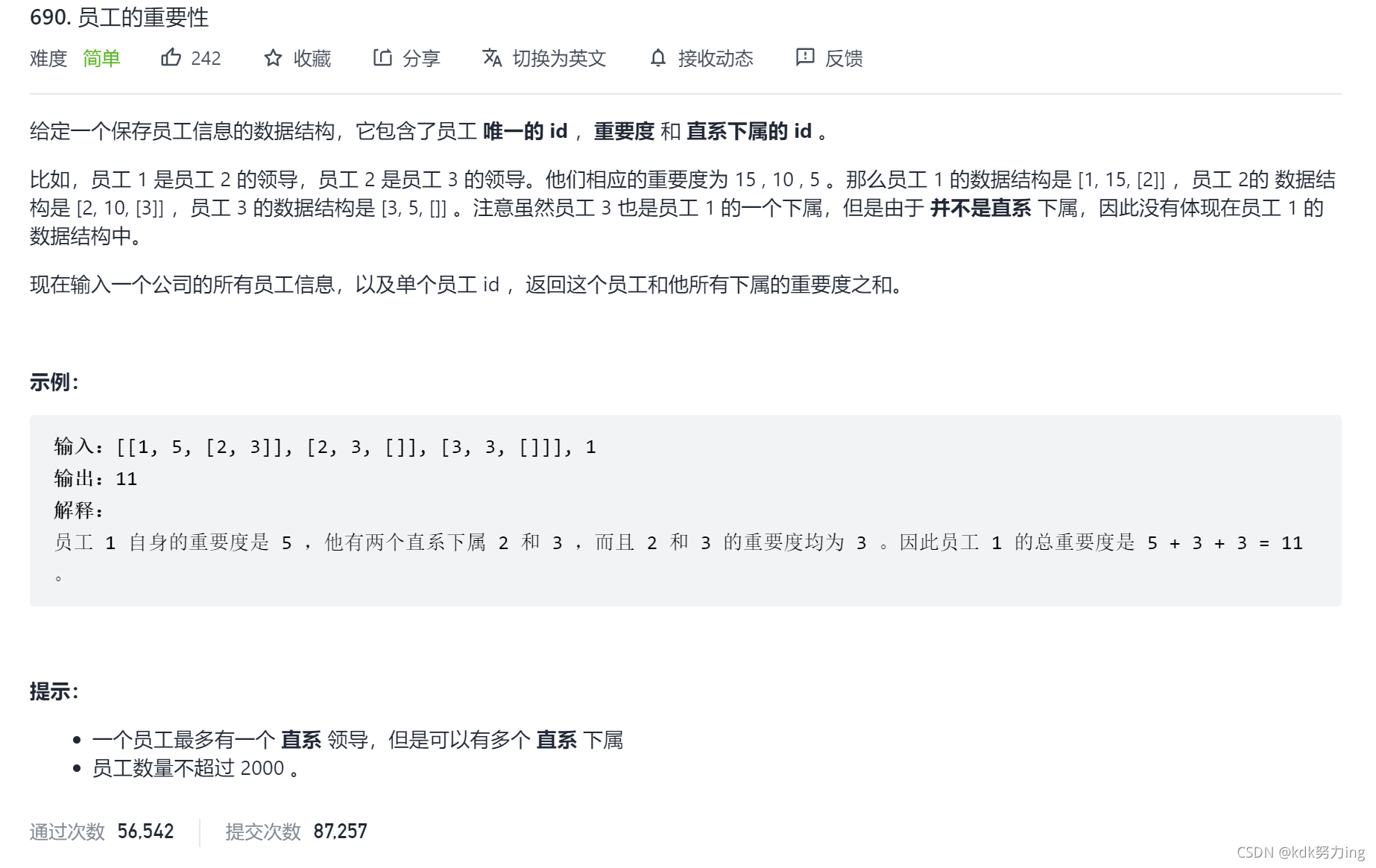
2021年10月29日18:45:32：

/*
// Definition for Employee.
class Employee {
    public int id;
    public int importance;
    public List<Integer> subordinates;
};
*/

class Solution {

    Map<Integer,Employee> map=new HashMap<>();  //建立员工编号和员工结构体的映射

    public int getImportance(List<Employee> employees, int id) {
        for(Employee e:employees) map.put(e.id,e);  //将所有员工和其结构体的映射
        return dfs(id); //从中员工开始往下递归，dfs的返回值就是这个员工和他所有下属的重要度之和。
    }

    public int dfs(int id){
        Employee e=map.get(id); //得到这个员工对应的结构体
        int res=e.importance;  //res就是这个员工和他所有下属的重要度之和，最一开始是只有id这一个员工
        for(Integer x:e.subordinates){  //枚举这个点的所有下属
            res+=dfs(x);  //再递归计算这个点的权值，结果加到res上
        }
        //当上面的for循环全部结束的时候，递归就会结束了，所以这里不用写递归结束语句，并且最后有return res语句
        return res; //全部递归完成之后返回res，即这个员工和他所有下属的重要度之和
    }
}