数据结构11:二叉树的数据类型和遍历方式

简介

前面我们讲了二叉树的结构，如图1所示。从图中我们可以看到，在二叉树中，每个节点最多有两个孩子，我们称为左孩子和右孩子；每个孩子又可以作为双亲拥有自己的孩子；以此规律多个节点可以组成一个棵大的树。

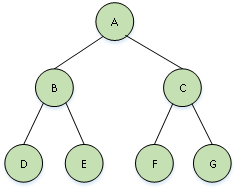
二叉树的数据结构

根据二叉树的特点，我们将二叉树的数据结构定义为：

typedef struct 
{
	int data;
	struct treeNode* lchild;
	struct treeNode* rchild;
}treeNode;

从二叉树的数据结构我们可以看出，data用于表示二叉树中的数据，该字段可以根据自己的实际需要进行修改；lchild和rchild分别是两个是指向二叉树类型的指针，用于指向左右孩子。我们在主函数中，建立一棵简单的二叉树，代码如下：

#include"stdio.h"
#include"stdlib.h"
#include"tree.h"

int main()
{
	treeNode treeNode0;
	treeNode treeNode1;
	treeNode treeNode2;
	treeNode0.data = 0;
	treeNode1.data = 1;
	treeNode2.data = 2;

	treeNode0.lchild = &treeNode1;
	treeNode0.rchild = &treeNode2;

	treeNode1.lchild = NULL;
	treeNode1.rchild = NULL;

	treeNode2.lchild = NULL;
	treeNode2.rchild = NULL;
	system("pause");
	return 0;
}

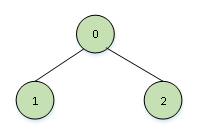
在代码中，我们定义了三个二叉树的节点，其中一个作为根节点，两个作为子节点，构成了一棵二叉树，如图2所示。

二叉树的遍历

二叉树的遍历是指从跟节点出发，按照某种次序以此访问二叉树中所有节点，使得每个节点都被访问一次且仅被访问一次。
二叉树常见的遍历方式有前序遍历、中序遍历、后序遍历和层次遍历。下面我们依次对这三种遍历方式进行介绍。

前序遍历

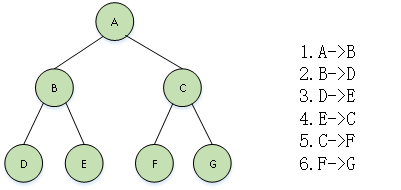
首先访问根结点然后遍历左子树，最后遍历右子树。在遍历左、右子树时，仍然先访问根结点，然后遍历左子树，最后遍历右子树。即：若二叉树为空则结束返回，否则：（1）访问根结点。 （2）前序遍历左子树 。（3）前序遍历右子树 。对于图1中的二叉树，前序遍历的顺序如图3所示，其遍历结果为:ABDECFG。

中序遍历

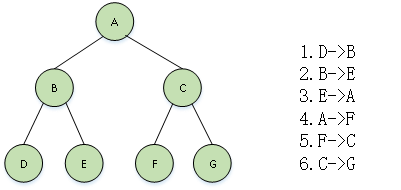
首先遍历左子树，然后访问根结点，最后遍历右子树。在遍历左、右子树时，仍然先遍历左子树，再访问根结点，最后遍历右子树。即： 若二叉树为空则结束返回，否则：（1）中序遍历左子树。（2）访问根结点。（3）中序遍历右子树。对于图1中的二叉树，中序遍历的顺序如图4所示，其遍历结果为：DBEAFCG。

后序遍历

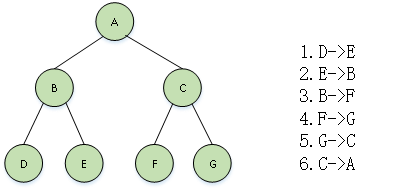
首先遍历左子树，然后遍历右子树，最后访问根结点。在遍历左、右子树时，仍然先遍历左子树，再遍历右子树，最后访问根结点。即： 若二叉树为空则结束返回，否则：（1）后序遍历左子树。 （2）后序遍历右子树。（3）访问根结点。对于图1中的二叉树，后序遍历的过程如图5所示，其遍历结果为：DEBFGCA。

层次遍历

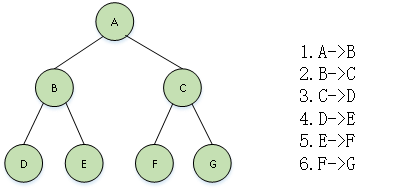
若树为空，结束返回；否则按照从从从上到下的顺序进行访问，同一层按照从左到右的顺序进行访问。对于图1中的二叉树，其层次遍历的顺序如图6所示，其遍历结果为：ABCDEFG。