算法导论学习笔记3_分治策略

---

1. 分治策略基本步骤

分治法的基本思想是：将原问题分解为几个规模较小但类似于原问题的子问题，递归地求解这些子问题，然后再合并这些子问题的解来建立原问题的解。

分治法的三个步骤是：
分解原问题为若干子问题，这些子问题都是原问题的规模较小的实例。
解决这些子问题，递归地求解各个子问题。当子问题足够小时，直接求解子问题。
合并这些子问题的解构成原问题的解。

当子问题足够大，需要递归求解时，称之为递归情况。
当子问题变得足够小，不再需要递归时，递归已经触底，进入了基本情况。

---

2. 归并排序

归并排序的步骤如下：
分解：将待排序的n个元素的序列分解为各具n/2个元素的两个子序列。
解决：使用归并排序递归地排序两个子序列。（当长度为1时停止递归。）
合并：合并两个已排序的子序列以产生已排序的序列。

其中，合并步骤是归并排序的关键步骤。假设两个已排序的子序列为$A[p..q]和A[q+1..r]$(注意两个子序列必定是相邻的)，首先创建两个临时数组$L[]$、$R[]$用于暂存两个子序列的数据，然后通过一个合并操作将$L[]$和$R[]$按升序合并到$A[p..r]$中。

下面是归并排序的伪代码，完整C++代码在文末附录中。

MERGE_SORT(A, p, r)
	if p < r // 元素个数大于1
		q = floor((p+r)/2) // 分解，向下取整
		MERGE_SORT(A, p, q) // 递归解决
		MERGE_SORT(A, q+1, r) // 递归解决
		MERGE(A, p, q, r)	// 合并

MERGE(A, p, q, r)
	n1 = q - p + 1
	n2 = r - q
	let L[1..n1 + 1] and R[1..n2 + 1] be new arrays
	for i = 1 to n1
		L[i] = A[p + i - 1]
	for j = 1 to n2
		R[j] = A[p + j]
	L[n1 + 1] = ∞
	R[n2 + 1] = ∞
	i = 1, j = 1
	for k = p to r
		if L[i] <= R[j]
			A[k] = L[i]
			i = i + 1
		else A[k] = R[j]
			j = j + 1

以序列{3, 1, 5, 9, 2, 4, 8, 7, 6, 10}为例，归并排序算法过程如下：

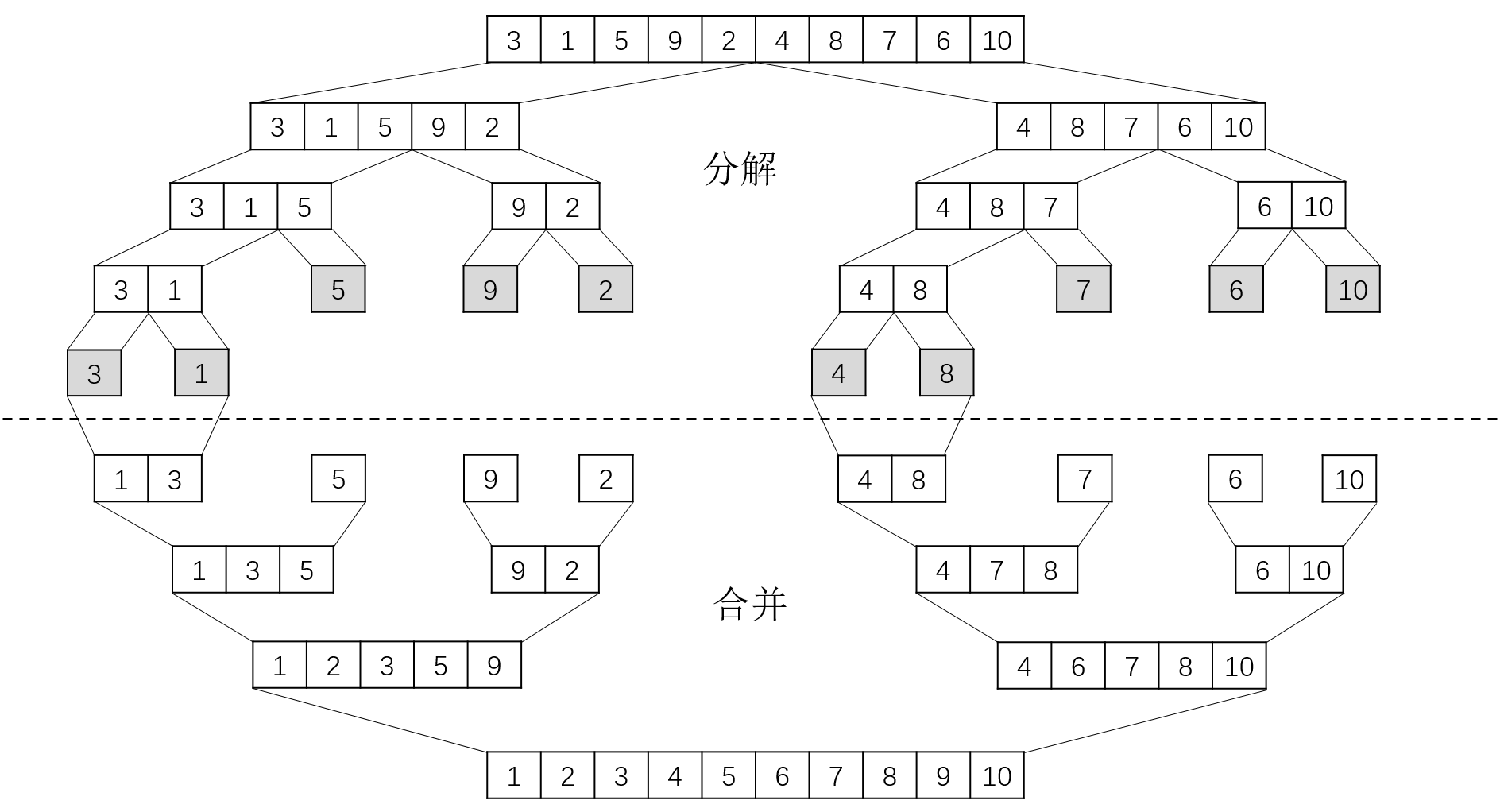
如上图所示，当子序列的元素个数大于1时，需通过递归求解，称为递归情况；当子序列的元素个数为1时（只有一个元素相当于已排序），递归触底，进入基本情况。

合并操作是上述算法的核心，通过将每一步递归时分解的两个子序列合并为一个递增的序列来实现排序。其中，合并操作由程序中的MERGE函数完成，程序中对两个已排序子序列扫描，并以此提取出两个序列中当前元素的较小值，最终得到一个非递减的序列。

3. 归并排序分析

由上面的过程可以看出，归并排序在序列的个数不是偶数时也能正常工作，下面为了简化分析，假设原问题的规模n为$2^k$，即2的幂。此外，还假设归并排序n个数的最坏情况运行时间为$T(n)$，当n>1时，可知：

分解：分解时只求解了子序列的中间位置，因此只需要常量时间，即$D(n)=\Theta (1)$。
解决：解决过程实际上时递归求解两个规模为n/2的子问题，因此需要$2T(n/2)$的运行时间。
合并：合并的过程中通过对两个子序列进行一次扫描，因此运行时间为$\Theta (n)$。

由以上分析可得，归并排序n个数的最坏情况运行时间T(n)的递推式为:
$$T(n)=\{\begin{array}{ll}\Theta (1)& n=1\\ 2T(n/2)+\Theta (n)& n>1\end{array}$$当n>1时，由递推式可得：
$$\begin{array}{rl}T(n)& =2T(n/2)+\Theta (n)\\ & =2(2T(n/4)+\Theta (n/2))+cn\\ & =2(2(2T(n/8)+\Theta (n/4))+cn/2)+cn\\ & =2(2(2(2T(n/16)+\Theta (n/8)))+cn/4)+cn/2)+cn\\ & \cdot \cdot \cdot \\ & =2(..(2T(1)+2c)+4c)+...+cn\end{array}$$
将上述关系绘制成递归树如下：

由上图可知，递归树的每一层的代价都是cn，因此只需要知道数的高度即可计算出运行时间T(n)的值。

其中，树的第i层的单个结点的代价为$cn/2^{i-1}$，由树的第k层叶子结点的代价为$c$可知$2^{k-1}=n$，因此树的高度$k=\lg n+1$，可得:$$T(n)=k\ast cn=(\lg n+1)\ast cn=cn\lg n+cn=\Theta (n\lg n)$$

因此，归并排序的最坏情况运行时间为$\Theta (n\lg n)$。

注：虽然上述分析中假设问题的规模为2的幂，但可以证明，当n的规模不是2的幂时并不影响归并排序所需时间的增长量级。

---

4. 最大子数组问题

最大子数组的描述如下：在一个序列中，如果连续若干个元素的和达到了最大，则称该数组为最大子数组。

上例中，{18,20,-7,12}为最大子数组，其和为43.

解决最大子数组问题最简单的方法就是枚举所有可能的起点和终点，计算子数组的和，从而找到和最大的子数组。对于元素为n的序列，可能的情况有$\left(\genfrac{}{}{0ex}{}{n+1}{2}\right)/2$种，且对于每种情况，计算子数组的和所需时间至少为常量时间，因此该算法的运行时间为$\Omega (n^2)$。

如果考虑使用分治策略来求解最大子数组问题，可将原问题分解为两个规模相同的子问题时，即像归并排序那样将序列分解为两个长度近似相同的子序列。按照分治法的思想，需要对分解、解决和合并三个步骤进行分析。

分解：将原数组分解为长度为n/2的两个子数组。
解决：此步骤不仅仅是递归解决两个子问题就能都达到目的，因为最大子数组可能存在两个子数组中，还可能跨越两个子数组，因此还需要单独计算跨越原数组中点的最大子数组。
合并：比较左子数组中的最大子数组、右子数组中的最大子数组以及跨越原数组中点的最大子数组，三者中的最大值即为原问题的解。

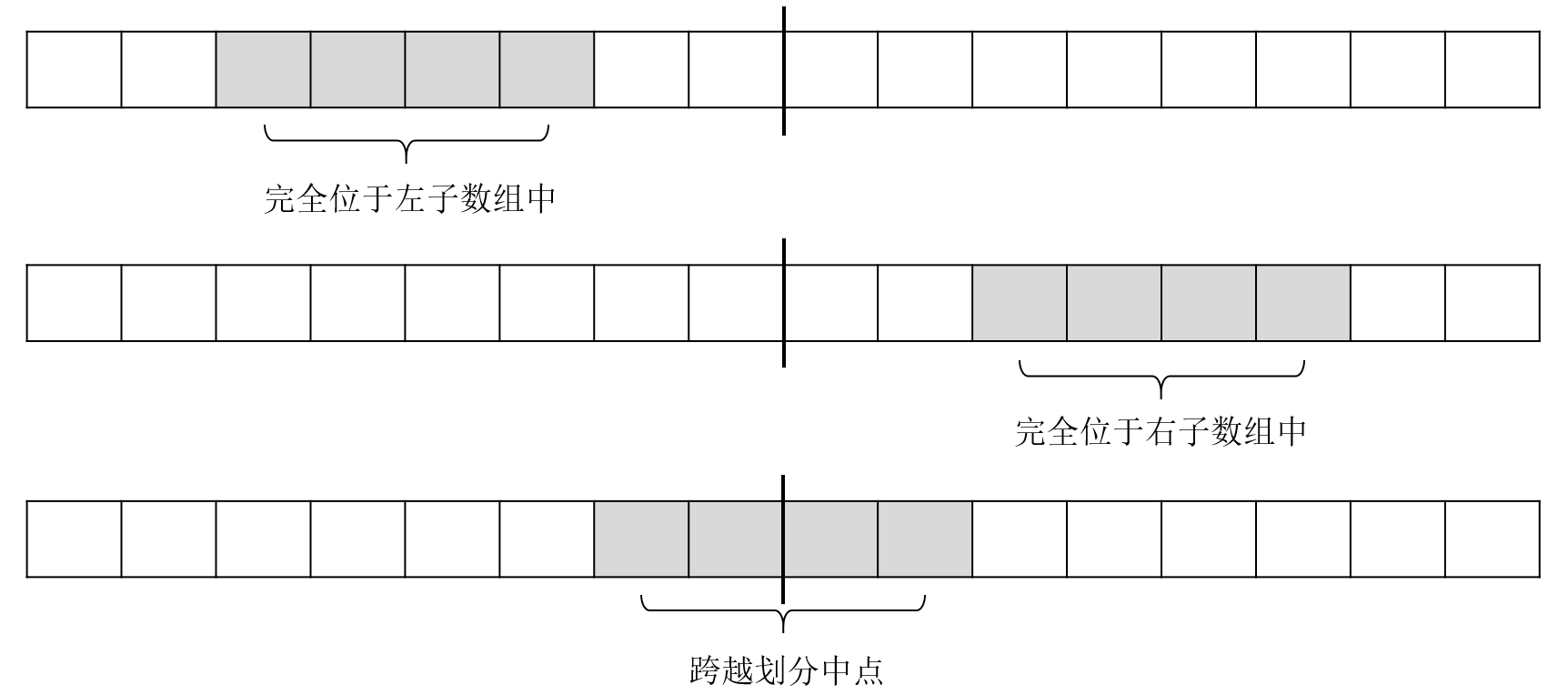
因此，最大子数组的分治算法的伪代码可以描述为：

FIND_MAXIMUM_SUBARRAY(A, low, high)
	if high == low
		return (low, high, A[low])
	else 
	    // 分解
		mid = floor((low + high) / 2) 
     	// 解决
		(low_left, high_left, sum_left) = FIND_MAXIMUM_SUBARRAY(A, low, mid) // 左
		(low_right, high_right, sum_right) = FIND_MAXIMUM_SUBARRAY(A, mid+1, high) // 右
		(low_cross, high_cross, sum_cross) = FIND_MAXIMUM_CROSS_SUBARRAY(A, low, mid, high) // 跨越中点
		// 合并
		if sum_left >= sum_right && sum_left >= sum_cross
			return (low_left, high_left, sum_left)
		if sum_rightt >= sum_left && sum_right >= sum_cross
			return (low_right, high_right, sum_right)
		else
			return (low_cross, high_cross, sum_cross)	 

其中，关键步骤为子程序FIND_MAXIMUM_CROSS_SUBARRAY，用于寻找跨越中点的最大子数组。这里只需要从中点A[mid]开始向左右扫描求和更新左右值即可。下面是该函数的伪代码，最大子数组问题的完整C++代码在文末的附录中。

FIND_MAXIMUM_CROSS_SUBARRAY(A, low, mid, high)
	left_sum = -∞
	sum = 0
	for i = mid downto low
		sum  = sum + A[i]
		if sum > left_sum
			max_left = i
	right_sum = -∞
	sum = 0
	for j = mid+1 to low
		sum  = sum + A[j]
		if sum > right_sum
			max_right = j
	return (max_left, max_right, left_sum + right_sum)

5. 最大子数组问题分析

对于n=1的基本情况，直接返回当前元素即可，因此所需时间为$\Theta (1)$。

对于n>1的递归情况（同样的假设n为2的幂），包括了分解、解决和合并三个步骤。
分解所需时间为$\Theta (1)$；
解决所需时间为递归求解所需时间$2T(n/2)$和"FIND_MAXIMUM_CROSS_SUBARRAY"所需时间$\Theta (n)$;
合并操作仅需常量时间$\Theta (1)$。

因此总得时间为：$2T(n/2)+\Theta (n)+\Theta (1)+\Theta (1)=2T(n/2)+\Theta (n)$

综上，最大子数组问题分治算法的运行时间递推式为：
$$T(n)=\{\begin{array}{ll}\Theta (1)& n=1\\ 2T(n/2)+\Theta (n)& n>1\end{array}$$通过对比归并排序的运行时间递推式可得此问题的运行时间也为$\Theta (n\lg n)$。

---

6. 递归式求解

在归并排序分析中，我们通过直接展开递归式和画递归树的方法来计算归并排序的运行时间。其中通过展开递归式的方法直接求解的方法通常比较复杂，而递归树的方法则是一种较为有效的方法。

此外，求解递归式还有代入法和主方法两种方法。

6.1 代入法

代入法求解递归式分为两步：
1.猜测：猜测解的形式
2.证明：用数学归纳法得到解中的常数，并证明解是正确的。

例如，确定下面递归式的上界：$$T(n)=2T(\lfloor n/2\rfloor )+n$$由于上式子和归并排序的递归式很相似，因此猜测其解为：$T(n)=O(n\lg n)$

因此需要证明：选择常数$c>0$，使得$T(n)\le cn\lg n$。下面利用数学归纳法证明：

假设$T(\lfloor n/2\rfloor )\le c\lfloor n/2\rfloor \lg (\lfloor n/2\rfloor )$,则有：$$\begin{array}{rl}T(n)& =2T(\lfloor n/2\rfloor )+n\\ & \le 2c\lfloor n/2\rfloor \lg (\lfloor n/2\rfloor )+n\\ & \le cn\lg (n/2)+n\\ & =cn\lg n-cn\lg 2+n\\ & =cn\lg n-cn+n\end{array}$$
当$c\ge 1$时，有$cn\ge n$，因此：$$T(n)\le cn\lg n$$

下面考虑数学归纳法的基本情况：

设$n=1$时为基本情况，且$T(1)=1$。不等式：$T(1)\le c\lg 1=0$显然不成立。

因此，$n=1$不能作为基本情况。由于渐近记号$O(n\lg n)$要求存在$c>0,n_0>0$，使得任意$n>n_0$，$T(n)\le cn\lg n$即可。

设$n=2$作为基本情况，$T(2)=2T(1)+2=4$。要使不等式：$T(2)\le c2\lg 2$成立，只需$c\ge 2$即可。

因此，存在$c\ge 2，n_0=2$,使得任意$n>n_0，T(n)\le cn\lg n$成立。

注：有的时候，我们猜出了正确的渐近界，却不能成功的用归纳法进行证明，这往往是因为做出的归纳假设不够强造成的。如下例：

考虑如下递归式：$$T(n)=T(\lfloor n/2\rfloor )+T(\lceil n/2\rceil )+1$$猜测解为$T(n)=O(n)$。

将$T(\lfloor n/2\rfloor )\le c\lfloor n/2\rfloor 、T(\lceil n/2\rceil )\le c\lceil n/2\rceil$带入递归式得：
$$T(n)\le c\lfloor n/2\rfloor +c\lceil n/2\rceil +1=cn+1$$通过上式不能得出$T(n)\le cn$，但$O(n)$又确实是上述递归式得的解。

这个时候应该做出更强的归纳假设，猜测$T(n)\le cn-d\le cn，d$是一个大于零的常数。

将$T(\lfloor n/2\rfloor )\le c\lfloor n/2\rfloor -d、T(\lceil n/2\rceil )\le c\lceil n/2\rceil -d$带入递归式得：$$T(n)\le c\lfloor n/2\rfloor +c\lceil n/2\rceil -2d+1=cn-2d+1$$
当上式中$d\ge 1$时,可得:$$T(n)\le cn-d\le cn$$

6.2 递归树法

递归树最适合用来生成好的猜测，然后即可用代入法来验证猜测是否正确。因此，利用递归树法来猜测递归式的解可以不必那么严谨，例如我们可以做出原问题的规模为2的幂等假设。

考虑递归式：$$T(n)=3T(\lfloor n/4\rfloor )+\Theta (n^2)$$
做出一步递归可由下递归树表示：

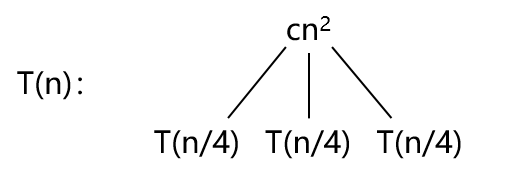
进一步递归：

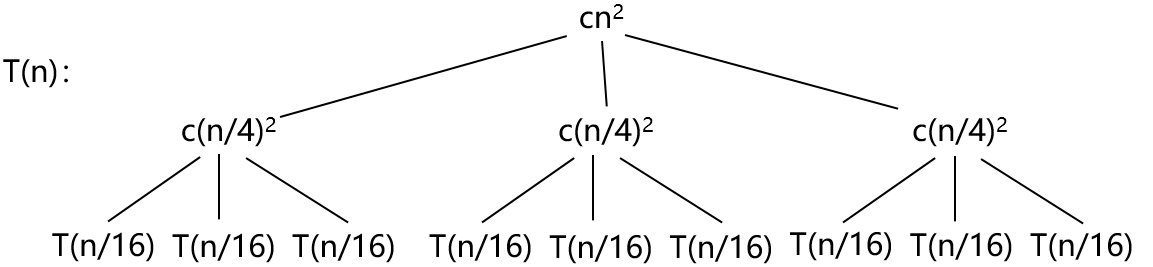
完整的递归树如下图所示：

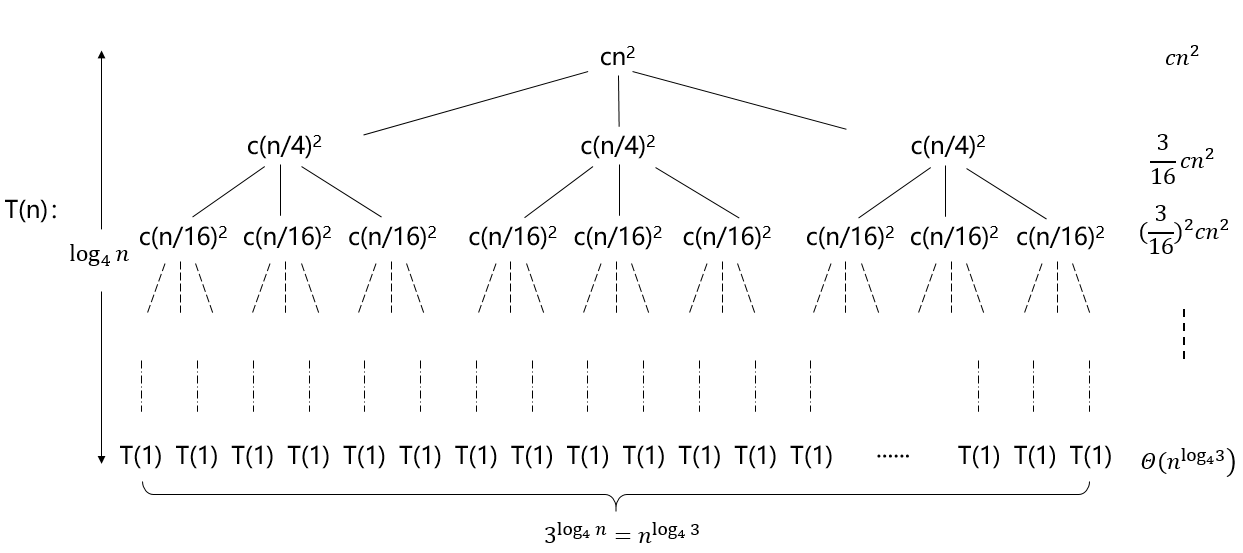
对所有层的代价求和：$$\begin{array}{rl}T(n)& =c{n}^2+\frac{3}{16}c{n}^2+(\frac{3}{16}{)}^{2}c{n}^2+\cdot \cdot \cdot +(\frac{3}{16}{)}^{lo{g}_{4}n-1}c{n}^2+\Theta (n^{lo{g}_{4}3})\\ & =\frac{1-(\frac{3}{16}{)}^{lo{g}_{4}n}}{1-\frac{3}{16}}c{n}^2+\Theta (n^{lo{g}_{4}3})\\ & \le \frac{1}{1-\frac{3}{16}}c{n}^2+\Theta (n^{lo{g}_{4}3})\\ & =\frac{16}{13}c{n}^2+\Theta (n^{lo{g}_{4}3})\\ & =O(n^2)\end{array}$$这里通过递归树法得到了一个渐近上界，然后利用代入法可证明上式成立，即$T(n)=O(n^2)$。

下面是递归树法的另一个更为复杂的例子：$$T(n)=T(n/3)+T(2n/3)+O(n)$$
递归树为：

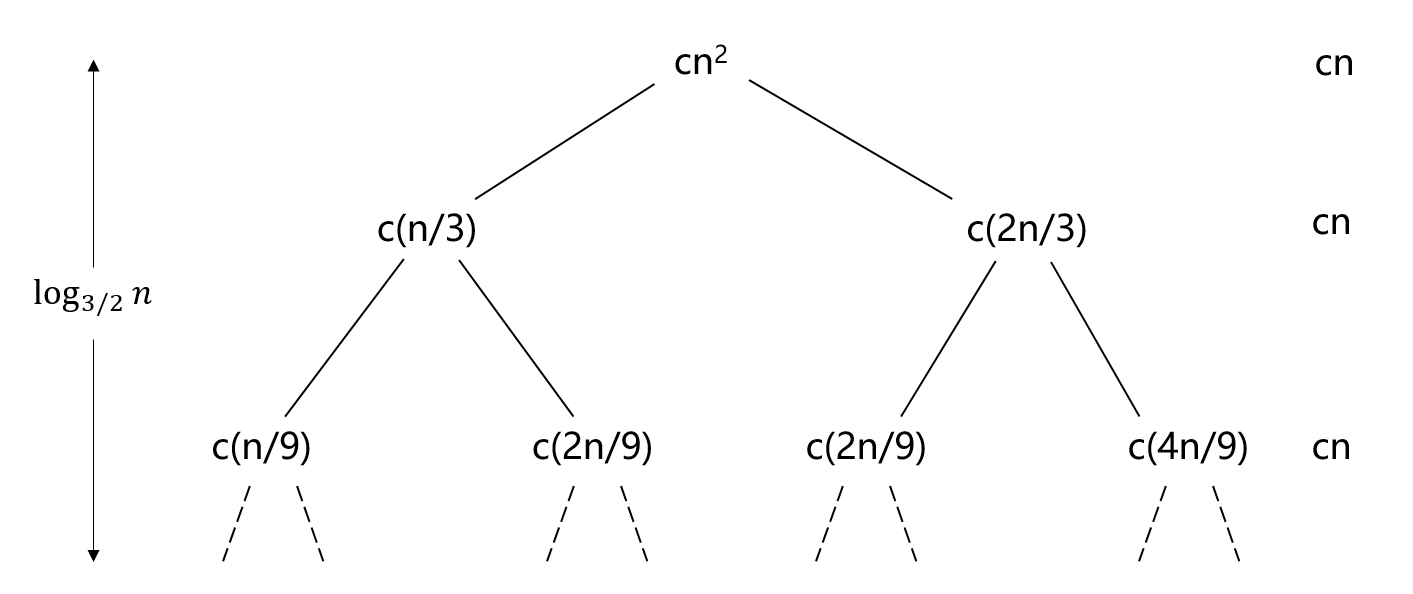
递归树的叶子结点最大深度为：${\log }_{3/2}n+1$
由于该递归树不是完全二叉树，因此可猜测一个渐近上界为：$O(cn{\log }_{3/2}n)=O(n\lg n)$。
利用代入法可验证$O(n\lg n)$确实是递归式解的一个上界。

6.3 主方法

主方法为如下形式的递归式提供了一种方便的求解方法：
$$T(n)=aT(n/b)+f(n)$$其中$a\ge 1$和$b>1$是常数，$f(n)$是渐近正函数。

注：上述递归式的含义为：将规模为$n$的问题分解为$a$个子问题，每个问题的规模为$n/b$。$a$个子问题又通过递归求解，每个子问题花费的时间为$T(n/b)$。函数$f(n)$包含了问题分解和子问题解合并的代价。

主定理：令$a\ge 1$和$b>1$是常数，$f(n)$是一个函数，T(n)是定义在非负整数上的递归式：
$$T(n)=aT(n/b)+f(n)$$其中，可将$n/b$解释为$\lfloor n/b\rfloor$或$\lceil n/b\rceil$。$T(n)$有如下渐近界：

1. 若对某个常数$ϵ>0$有$f(n)=O(n^{{\log }_{b}a-ϵ})$，则$T(n)=\Theta (n^{{\log }_{b}a})。$
2. 若$f(n)=\Theta (n^{{\log }_{b}a})$，则$T(n)=\Theta (n^{{\log }_{b}a}\lg n)$。
3. 若对某个常数$ϵ>0$有$f(n)=\Omega (n^{{\log }_{b}a+ϵ})$，且对某个常数$c<1$和所有足够大的$n$有$af(n/b)\le cf(n)$，则$T(n)=\Theta (f(n))$。

例1：$$T(n)=9T(n/3)+n$$上式中，$a=9,b=3,f(n)=n$，因此$n^{{\log }_{b}a}=n^{{\log }_{3}9}=n^2$，则$f(n)=n=\Theta (n^{{\log }_{3}9-1})$，落入情况1，因此$T(n)=\Theta (n^{{\log }_{b}a})=\Theta (n^2)$。

例2：$$T(n)=T(2n/3)+1$$上式中，$a=1,b=3/2,f(n)=1$，因此$n^{{\log }_{b}a}=n^{{\log }_{3/2}1}=n^0=1$，则$f(n)=1=\Theta (n^{{\log }_{3/2}1})$，落入情况2，因此$T(n)=\Theta (\lg n)$。

例3：$$T(n)=3T(n/4)+n\lg n$$上式中，$a=3,b=4,f(n)=n\lg n$，因此$n^{{\log }_{b}a}=n^{{\log }_{4}3}=n^{0.793}$，则$f(n)=n\lg n=\Omega (n^{{\log }_{4}3+ϵ})$。
下面判断正则条件：
$$af(n/b)=3n/4\lg (n/4)=3n/4(\lg n-\lg 4)\le 3n/4\lg n=3/4f(n)$$因此可取$c=3/4<1$，使得对于所有足够大的$n$，有$af(n/b)\le cf(n)$，因此$T(n)=\Theta (f(n))=\Theta (n\lg n)$。

例4：
$$T(n)=2T(n/2)+n\lg n$$上式中，$a=2,b=2,f(n)=n\lg n$，因此$n^{{\log }_{b}a}=n^{{\log }_{2}2}=n$，则$f(n)=n\lg n=\Omega (n^{1+ϵ})$。
正则条件：
$$af(n/b)=2n/2\lg (n/2)=n\lg (n/2)\le cn\lg n$$
要使上式对于足够大的n恒成立，则：
$$\frac{n\lg (n/2)}{cn\lg n}=\frac{n\lg n-n}{cn\lg n}=\frac{\lg n-1}{c\lg n}$$恒成立，因此$c\ge 1$，不满足正则条件，因此此递归式不能用主方法求解。

---

7. 附录

7.1 归并排序代码

#include "merge_sort.h"
#include <climits>
#include <cstring>
void merge(int *A, int p, int q, int r) {
	int n1 = q - p + 1;
	int n2 = r - q;
	int *L = new int[n1 + 2]; //L[0]/R[0]舍弃不用
	int *R = new int[n2 + 2];
	L[n1 + 1] = R[n2 + 1] = INT_MAX;
	memcpy(L + 1, A + p, n1*sizeof(int));
	memcpy(R + 1, A + q + 1, n2*sizeof(int));
	int i = 1; int j = 1;
	for (int k = p; k <= r; k++) {
		if (L[i] < R[j])
			A[k] = L[i++];
		else A[k] = R[j++];
	}
	delete []L;
	delete []R;
}
void merge_sort(int *A, int p, int r) {
	if(p < r){
		int q = (int)((p + r) / 2);
		merge_sort(A, p, q);
		merge_sort(A, q + 1, r);
		merge(A, p, q, r);
	}
}

7.2 最大子数组代码

#include "max_subarray.h"
#include <climits>
typedef struct max_struct{
    int left;
    int right;
    int sum;
}max_struct;

max_struct find_max_crossing_subarray(int *A, int low, int mid, int high){
    int left_sum = - INT32_MAX, right_sum = - INT32_MAX;
    int sum = 0;
    max_struct max;
    max.left = max.right = 0;
    for(int i = mid; i >= low; i--){
        sum = sum + A[i];
        if(sum > left_sum){
            left_sum = sum;
            max.left = i;
        }
    }
    sum = 0;
    for(int i = mid + 1; i <= high; i++){
        sum = sum + A[i];
        if(sum > right_sum){
            right_sum = sum;
            max.right = i;
        }
    }
    max.sum = left_sum + right_sum;
    return max;
}
max_struct find_max_subarray(int *A, int low, int high){
    int mid = 0;
    max_struct temp;
    if(low == high){
        temp.left = low;
        temp.right = high;
        temp.sum = A[low];
        return temp;
    }else{
        mid = (low + high) / 2;
        max_struct left = find_max_subarray(A, low, mid);
        max_struct right = find_max_subarray(A, mid + 1, high);
        max_struct cross = find_max_crossing_subarray(A, low, mid, high);
        if(left.sum >= right.sum && left.sum >= cross.sum)
            return left;
        else if(right.sum >= left.sum && right.sum >= cross.sum)
            return right;
        else return cross;
    }
        
}