算法导论学习笔记11_红黑树

最新推荐文章于 2019-12-03 16:48:25 发布

WavenZ

最新推荐文章于 2019-12-03 16:48:25 发布

阅读量199

点赞数

分类专栏：算法文章标签：红黑树算法导论

本文链接：https://blog.csdn.net/weixin_43374723/article/details/89058282

版权

算法专栏收录该内容

23 篇文章 4 订阅

订阅专栏

红黑树

1. 红黑树的性质
2. 搜索树的旋转
3. 红黑树的插入
4. 红黑树中结点的删除
5. 附录（代码）

1. 红黑树的性质

红黑树是一棵二叉搜索树，它在每个结点上增加了一个存储位来表示结点的颜色（BLACK或RED）。通过对任何一条从根到叶子的简单路径上各个结点的颜色进行约束，红黑树可确保没有一条路径会比其他路径长2倍，因此红黑树近似为一棵平衡二叉搜索树。

红黑树满足下列5条性质：

每个结点为红色或者黑色。
根节点为黑色。
每个叶结点都是黑色。
红色结点的子结点必为黑色。
对于每个结点，从该结点到其后代所有叶结点的简单路径上，均包含相同数量的黑色结点。

注1：其中前三条性质比较容易维护，而后两条性质在插入或者删除的时候很容易被破坏。
注2：红黑树中的叶结点指的是NIL结点，而不是普通树中定义的叶结点，如下图。

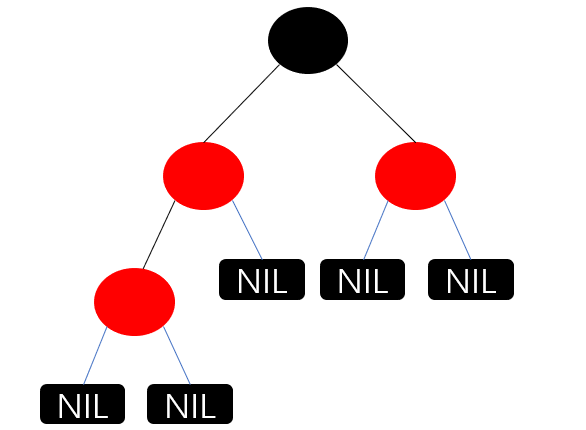
(绘制红黑树的图时通常会省略NIL结点)

一棵典型的红色树如下图所示：

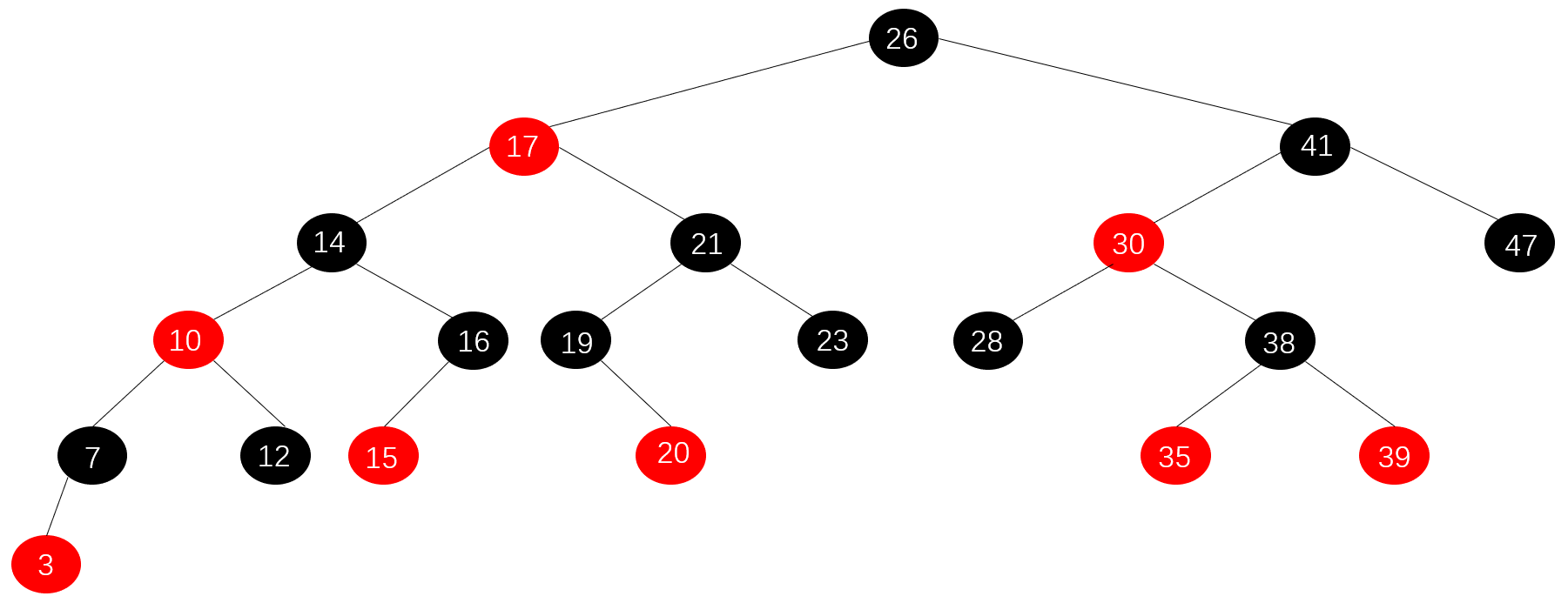
可以看到，红黑树不仅要满足上面提及的几条性质之外，还需要满足二叉搜索树的性质：

若任意结点的左子树不为空，则左子树上所有结点的值均小于其根节点上的值。
若任意结点的右子树不为空，则右子树上所有结点的值均大于其根节点上的值。
任意结点的左右子树也称为二叉搜索树。
二叉搜索树中没有关键字相同的结点。

此外，一棵红色树的高度满足： $h\le2\lg(n+1)$ 其中， $n$ 为红黑树内部结点的个数。由该性质可得，搜索、插入、删除等操作可在 $O(\lg n)$ 时间内完成。

2. 搜索树的旋转

当我们向红黑树中插入或者删除结点时，通常会不可避免的破坏红黑树的性质。因此，我们通常采取一些措施来维护被破坏的性质，常用的操作是变色和旋转。

这里，为了在维护红黑树的性质的同时不破坏二叉搜索树的性质，因此这里的旋转操作不能改变结点的前驱后继关系。

下图展示了旋转操作的示意图，包括左旋和右旋：

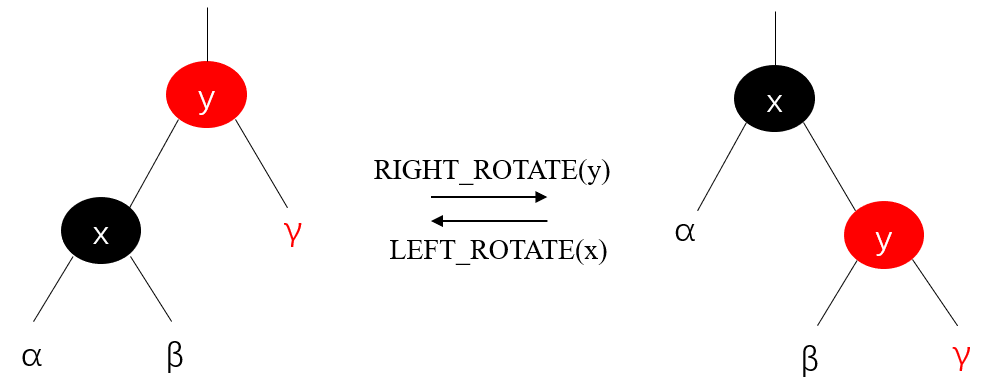
上图中，对左图进行中序遍历的结果为 $\{\alpha, x, \beta, y, \gamma\}$ ，对右图进行中序遍历的结果也为 $\{\alpha, x, \beta, y, \gamma\}$ 。因此，旋转操作保持二叉搜索树的性质。

下面是旋转操作的伪代码：

LEFT_ROTATE(T, x)
	y = x.right
	x.right = y.left
	if y.left != T.nil
		y.left.p = x
	y.p = x.p
	if x.p == T.nil
		T.root = y
	elseif x == x.p.left
		x.p.left = y
	else x.p.right = y
	y.left = x
	x.p = y
RIGHT_ROTATE(T, y)
	x = y.left
	y.left = x.right
	if x.right != T.nil
		x.right.p = y
	x.p = y.p
	if y.p == T.nil
		T.root = x
	elseif y == y.p.right
		y.p.right = x
	else y.p.left = x
	x.rigtht = y
	y.p = x

3. 红黑树的插入

向红黑树中插入元素的过程和向二叉搜索树中插入元素的过程类似，不过在红黑树中插入元素可能造成红黑树的性质遭到破坏，因此还需要增加维护红黑树性质的操作。

下面的伪代码向红黑树中插入结点并标记为红色，然后利用RB_INSERT_FIXUP来维护红黑树的性质：

RB_INSERT(T, z)
	y = T.nil
	x = T.root
	while x != T.nil
		y = x
		if z.key < x.key
		x = x.left
		else x = x.right
	z.p = y
	if y == T.nil
		T.root = z
	elseif z.key < y.key
		y.left = z
	else y.right = z
	z.left = T.nil
	z.right = T.nil
	z.color = RED
	RB_INSERT_FIXUP(T, z)

由于插入的新结点初始标记为红色，因此可能破坏的性质为性质2和性质4。
①当插入的结点为根节点时，破坏了性质2；
②当插入的结点的父结点为红色时，破坏了性质4；

对于①，只需要将根节点置为黑色即可。
对于②，因为插入的结点及其父结点都为红色，因此按其叔结点颜色的不同分为以下两类（下面就插入结点的父结点是其祖父结点的左孩子结点为例讨论，与其为右孩子是对称的情况）：
$\space\space\space\space\space\space\space\space\space\space\space\space\space\space$ 类型1：叔父结点为红色，则只需要将其父结点和叔结点置为黑色并将其祖父结点置为红色即可。由于其祖父结点由红色变为黑色的同时可能违反红黑树的性质，因此需要针对其祖父结点进行红黑树性质的维护。

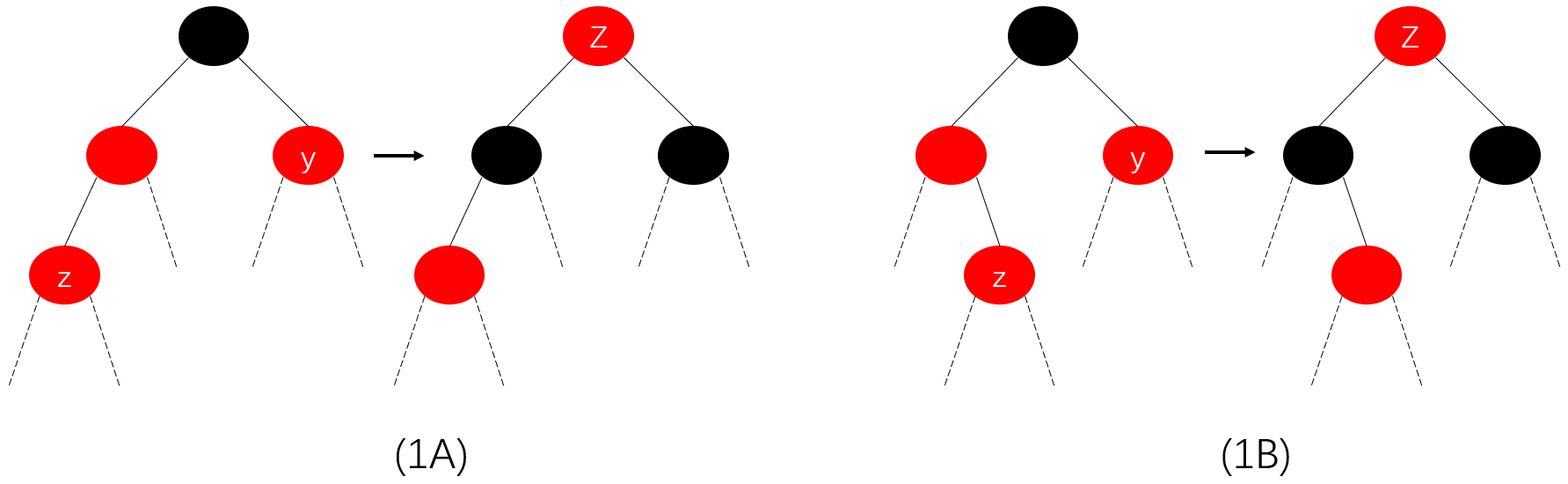
上图中，z的叔结点y为红色结点，因此对结点z的父结点和叔结点置为黑色，而将其祖父结点置为红色，然后向其祖父结点递归维护红黑树的性质。
$\space\space\space\space\space\space\space\space\space\space\space\space\space\space$ 类型2：叔父结点为黑色，这个时候还需要分两种情况讨论：
$\space\space\space\space\space\space\space\space\space\space\space\space\space\space$ 1.插入结点是其父结点的左孩子：将父结点置为黑色、祖父结点置为红色，并绕祖父结点进行右旋。

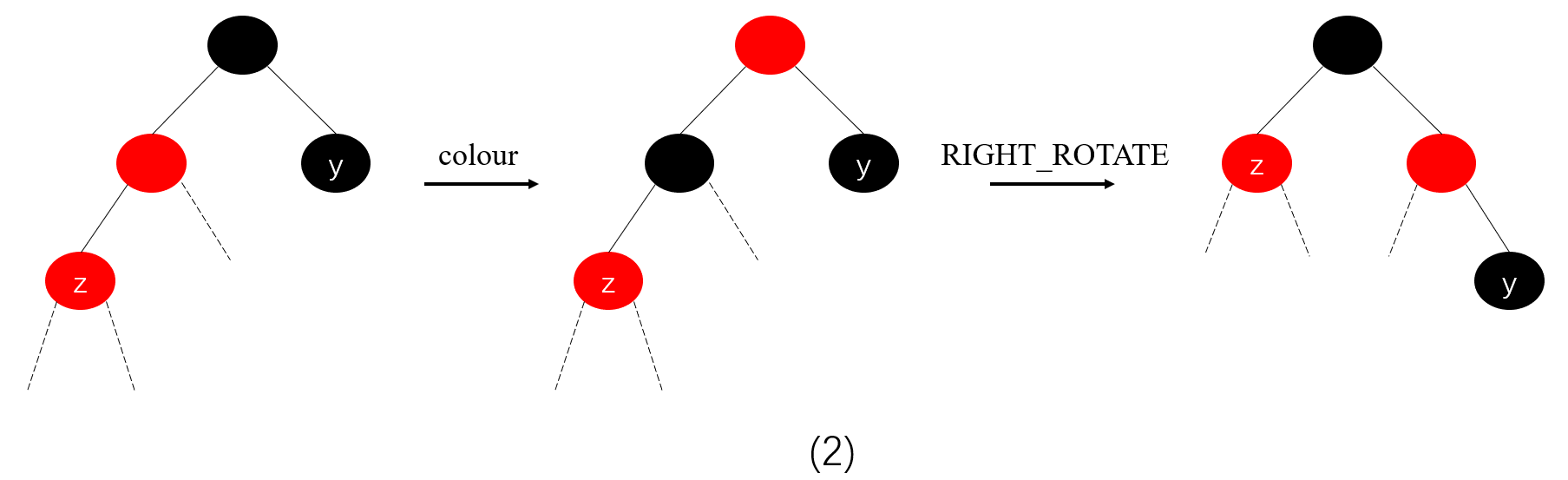
$\space\space\space\space\space\space\space\space\space\space\space\space\space\space$ 2.插入结点是其父结点的右孩子：直接绕其父结点左旋，变为上面的情形1。

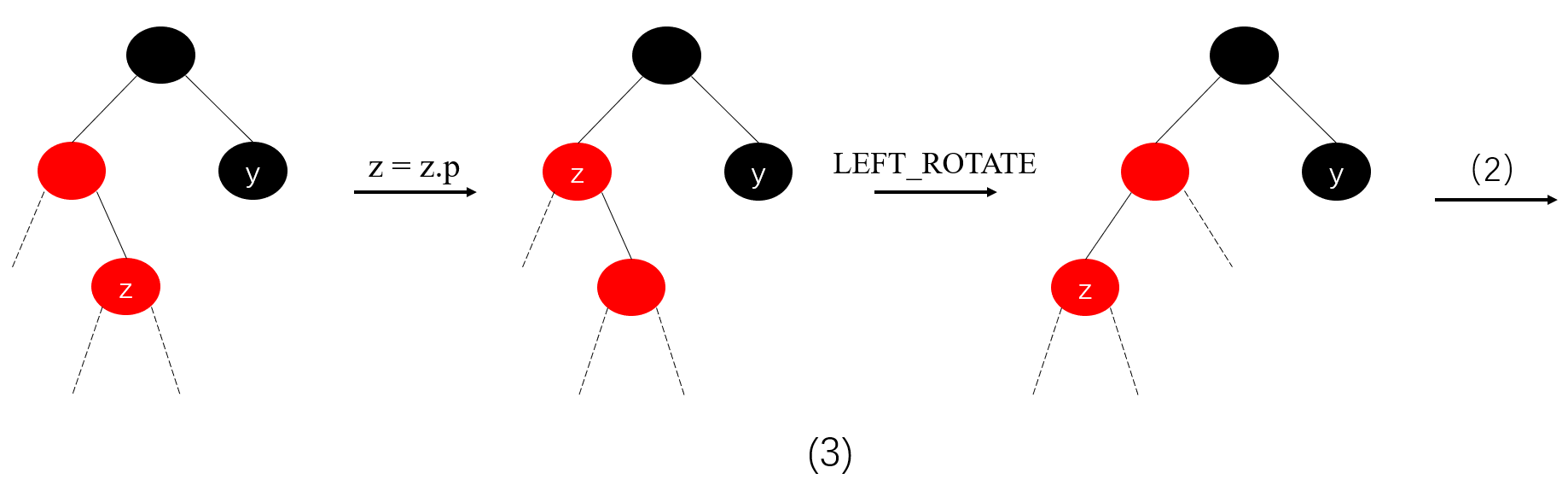
综上，对于向红黑树中插入的情况可分为三种情况，分别对应上面三个图：(1A)+(1B)、(2)、(3)。其中，对于情况(1)时，采用换色策略将可能违反规则的结点向树根传递；对于情况(2)，采用换色和旋转策略直接修复被破坏的性质；对于情况(3)，通过旋转转换为情况(2)。

下面是红黑树插入时维护红黑树性质的子过程伪代码：

RB_INSERT_FIXUP(T, z)
	while z.p.color = RED
		if z.p == z.p.p.left
			y = z.p.p.right
			if y.color == RED                //case 1
				z.p.color = BLACK            //case 1
				y.color = BLACK              //case 1
				z.p.p.color = RED            //case 1
				z = z.p.p                    //case 1
			else if z == z.p.right           //case2 & case 3 
						z = z.p              //case 3
						LEFT_ROTATE(T, z)    //case 3
				z.p.color = BLACK            //case 2
				z.p.p.color = RED            //case 2
				z = z.p.p                    //case 2
			RIGHT_ROTATE(T, z.p.p)           //case 2
		else(same as then clause
					with "right" and "left" exchanged)
	T.root.color = BLACK

注：当y.color = RED成立时，对应情况1，执行6-9行；否则为情况(2)或(3)，当z == z.p.right不成立时，对应情况(2)，执行13-16行，否则为情况(3)，执行11-16行。

4. 红黑树中结点的删除

在红黑树中删除结点的过程和在平衡二叉树中删除结点的过程同样类似，不同的是删除结点的同时不仅要维护二叉搜索树的性质，还需要维护红黑树的性质。在红黑树中删除结点的过程与插入相比要更复杂一些，因为删除的过程中不仅会破坏性质2和4，还可能破坏性质5。

下面直接给出删除操作的伪代码：

RB_TRANSPLANT(T, u, v)
	if u.p == T.nil
		T.root = v
	elseif  u == u.p.left
		u.p.left = v
	else u.p.right = v
	v.p = u.p
RB_DELETE(T, z)
	y = z
	y_original_color = y.color
	if z.left == T.nil
		x = z.right
		RB_TRANSPLANT(T, z, z.right)
	elseif z.right == T.nil
		x = z.left
		RB_TRANSPLANT(T, z, z.left)
	else y = TREE_MINIMUM(z.right)
		y_original_color = y.color
		x = y.right
		if y.p = z
			x.p = y
		else RB_TRANSPLANT(T, y, y.right)
			y.right = z.right
			y.right.p = y
		RB_TRANSPLANT(T, z, y)
		y.left = z.left
		y.left.p = y
		y.color = z.color
	if y_original_color = BLACK
		RB_DELETE_FIXUP(T, x)
RB_DELETE_FIXUP(T, z)
	while x != T.root and x.color == BLACK
		if x == x.p.left
			w = x.p.right
			if w.color == RED							
				w.color = BLACK											//case 1
				x.p.color = RED					                        //case 1
				LEFT_ROTATE(T, x.p)                                     //case 1
				w = x.p.right                                           //case 1
			if w.left.colot == BLACK and w.right.color == BLACK
				w.color = RED				                            //case 2
				x = x.p						                            //case 2
			else if w.right.color == BLACK
						w.left.color = BLACK			                //case 3
						w.color = RED						            //case 3
						RIGHT_ROTATE(T, w)                              //case 3
						w = x.p.right                                   //case 3
				w.color = x.p.color                                     //case 4
				x.p.color = BLACK                                       //case 4
				w.right.color = BLACK                                   //case 4
				LEFT_ROTATE(T, x.p)                                     //case 4
				x = T.root                                              //case 4
		else (same as then clause with "right" and "left" exchanged)
	x.color = BLACK

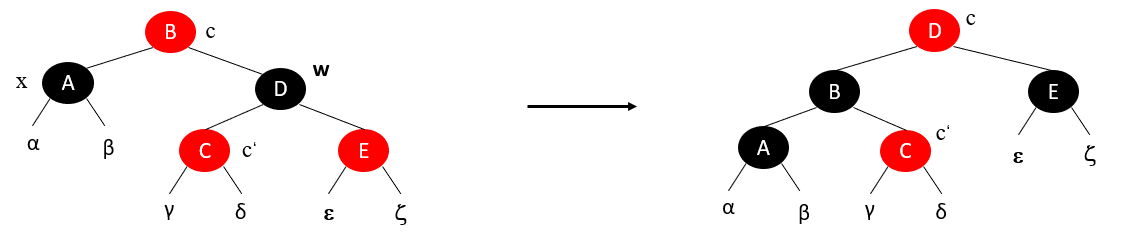
其中，RB_DELETE_FIXUP中的case1234分别对应以下四中情况：
情况1：x的兄弟结点w是红色的

情况2：x的兄弟结点w是黑色的，而且w的两个子结点都是黑色的

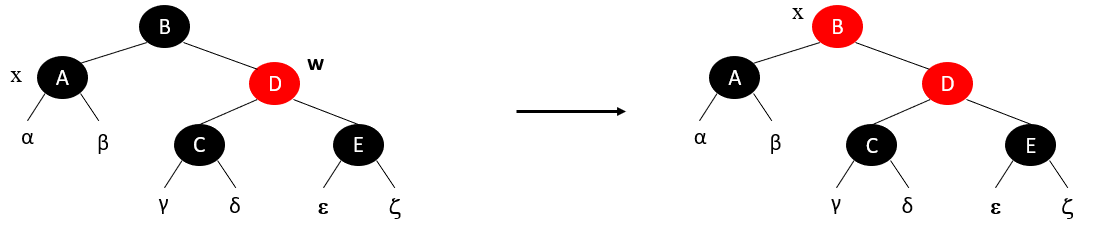
情况3：x的兄弟结点w是黑色的，w的左孩子是红色的，w的右孩子是黑色的

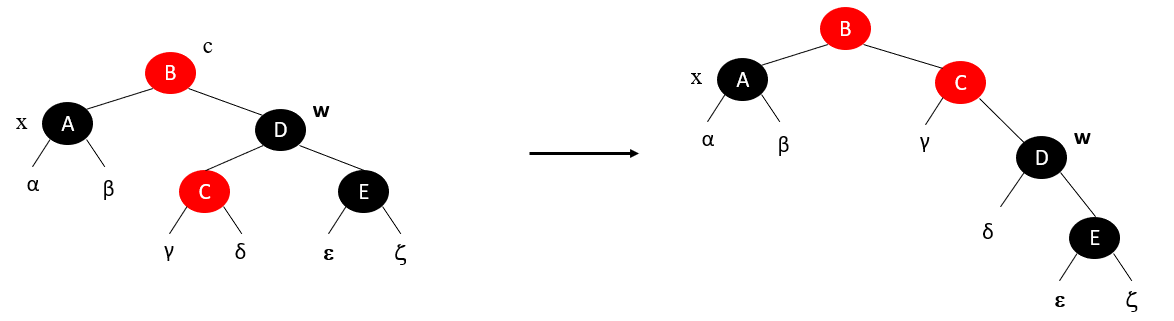
情况4：x的兄弟结点w是黑色的，且w的右孩子是红色的

5. 附录（代码）

下面是红黑树的C++实现，包含最基本的Build、Insert、Delete、Traverse、Search等操作。

#include <iostream>
#include <vector>
using namespace std;

enum Color{BLACK, RED};
struct Node{
	Node* p = nullptr;
	Node* left = nullptr;
	Node* right = nullptr;
	Color color = RED;
	int key;
};
class RB_Tree {
private:
	typedef void(*callback)(Node*);
	Node* Min(Node* node);
	void Left_rotate(Node* node);
	void Right_rotate(Node* node);
	void Transplant(Node* u, Node* v);
	void Insert_fixup(Node* node);
	void Delete_fixup(Node* node);
public:
	Node *root = nullptr;
	Node *nil = nullptr;
	void Insert(int key);
	void Delete(int key);
	void Build(vector<int>);
	void Traverse(Node* T, callback visit);
	Node* Search(int key);
};
Node* RB_Tree::Search(int key) {
	Node* x = root;
	while (x != nil) {
		if (key == x->key) return x;
		else if (key < x->key) x = x->left;
		else x = x->right;
	}
	return nullptr;
}
Node* RB_Tree::Min(Node* node) {
	Node* x = node;
	Node* y = node;
	while (x != nil) {
		y = x;
		x = x->left;
	}
	return y;
}
void RB_Tree::Traverse(Node* T, callback visit) {
	if (T != nil) {
		Traverse(T->left, visit);
		visit(T);
		Traverse(T->right, visit);
	}
}
void RB_Tree::Left_rotate(Node* node) {
	Node* y = node->right;
	node->right = y->left;
	if (y->left != nil) y->left->p = node;
	y->p = node->p;
	if (node->p == nil) root = y;
	else if (node == node->p->left) node->p->left = y;
	else node->p->right = y;
	y->left = node;
	node->p = y;
}
void RB_Tree::Right_rotate(Node* node) {
	Node* y = node->left;
	node->left = y->right;
	if (y->right != nil) y->right->p = node;
	y->p = node->p;
	if (node->p == nil) root = y;
	else if (node == node->p->right) node->p->right = y;
	else node->p->left = y;
	y->right = node;
	node->p = y;
}
void RB_Tree::Transplant(Node* u, Node* v) {
	if (u->p == nil) root = v;
	else if (u == u->p->left) u->p->left = v;
	else u->p->right = v;
	v->p = u->p;
}
void RB_Tree::Insert_fixup(Node* node) {
	while (node->p->color == RED) {
		if (node->p == node->p->p->left) {
			Node* y = node->p->p->right;
			if (y->color == RED) {
				node->p->color = BLACK;
				y->color = BLACK;
				node->p->p->color = RED;
				node = node->p->p;
			}
			else {
				if (node == node->p->right) {
					node = node->p;
					Left_rotate(node);
				}
				node->p->color = BLACK;
				node->p->p->color = RED;
				Right_rotate(node->p->p);
			}
		}
		else {
			Node* y = node->p->p->left;
			if (y->color == RED) {
				node->p->color = BLACK;
				y->color = BLACK;
				node->p->p->color = RED;
				node = node->p->p;
			}
			else {
				if (node == node->p->left) {
					node = node->p;
					Right_rotate(node);
				}
				node->p->color = BLACK;
				node->p->p->color = RED;
				Left_rotate(node->p->p);
			}
		}
	}
	root->color = BLACK;
}
void RB_Tree::Insert(int key) {
	Node* x = root;
	Node* y = nil;
	Node* node = new Node{ nil, nil, nil, RED, key };
	while (x != nil) {
		y = x;
		if (key == x->key) return;
		else if (key < x->key) 
			x = x->left;
		else 
			x = x->right;
	}
	node->p = y;
	if (y == nil) root = node;
	else if (node->key < y->key) y->left = node;
	else y->right = node;
	Insert_fixup(node);
}
void RB_Tree::Delete_fixup(Node* node) {
	Node* x = node;
	while (x != nullptr && x->color == BLACK) {
		if (x == x->p->left) {
			Node* w = x->p->right;
			if (w->color == RED) {
				w->color = BLACK;
				x->p->color = RED;
				Left_rotate(x->p);
				w = x->p->right;
			}
			if (w->left->color == BLACK && w->right->color == BLACK)
			{
				w->color = RED;
				x = x->p;
			}
			else {
				if (w->right->color == BLACK) {
					w->left->color = BLACK;
					w->color = RED;
					Right_rotate(w);
					w = x->p->right;
				}
				w->color = x->p->color;
				x->p->color = BLACK;
				w->right->color = BLACK;
				Left_rotate(x->p);
				x = root;
			}
		}
		else {
			Node* w = x->p->left;
			if (w->color == RED) {
				w->color = BLACK;
				x->p->color = RED;
				Right_rotate(x->p);
				w = x->p->left;
			}
			if (w->right->color == BLACK && w->left->color == BLACK)
			{
				w->color = RED;
				x = x->p;
			}
			else {
				if (w->left->color == BLACK) {
					w->right->color = BLACK;
					w->color = RED;
					Left_rotate(w);
					w = x->p->left;
				}
				w->color = x->p->color;
				x->p->color = BLACK;
				w->left->color = BLACK;
				Right_rotate(x->p);
				x = root;
			}
		}
	}
	x->color = BLACK;
}
void RB_Tree::Delete(int key) {
	Node* node = Search(key);
	Node* x = nullptr;
	Node* y = node;
	Color y_original_color = y->color;
	if (node->left == nullptr) {
		x = node->right;
		Transplant(node, node->right);
	}
	else if (node->right == nullptr) {
		x = node->left;
		Transplant(node, node->left);
	}
	else{
		y = Min(node->right);
		y_original_color = y->color;
		x = y->right;
		if (y->p == node) x->p = node;
		else {
			Transplant(y, y->right);
			y->right = node->right;
			y->right->p = y;
		}
		Transplant(node, y);
		y->left = node->left;
		y->left->p = y;
		y->color = node->color;
	}
	if (y_original_color == BLACK)
		Delete_fixup(x);
}
void RB_Tree::Build(vector<int> data) {
	root = nil = new Node{ nullptr, nullptr, nullptr, BLACK, 0 };
	for (int i : data) {
		Insert(i);
	}
}

void visit(Node* node) {
	if (node->color == BLACK)
		cout << node->key << ",BLACK   ";
	else cout << node->key << ",RED     ";
}
int main(int argc, char* argv[]) {
	vector<int> data = { 7, 2, 8, 3, 6, 4, 3, 1, 5, 9, 0 };
	RB_Tree T;
	T.Build(data);
	T.Traverse(T.root, visit);
	cout << endl;
	T.Delete(5);
	T.Traverse(T.root, visit);
	cout << endl;
	if (T.Search(3)) cout << "success!" << endl;
	return 0;
}

代码输出为：

0,RED     1,BLACK   2,RED     3,RED     4,RED     5,BLACK   6,RED     7,BLACK   8,BLACK   9,RED
0,RED     1,BLACK   2,RED     3,RED     4,RED     6,BLACK   7,BLACK   8,BLACK   9,RED
success!

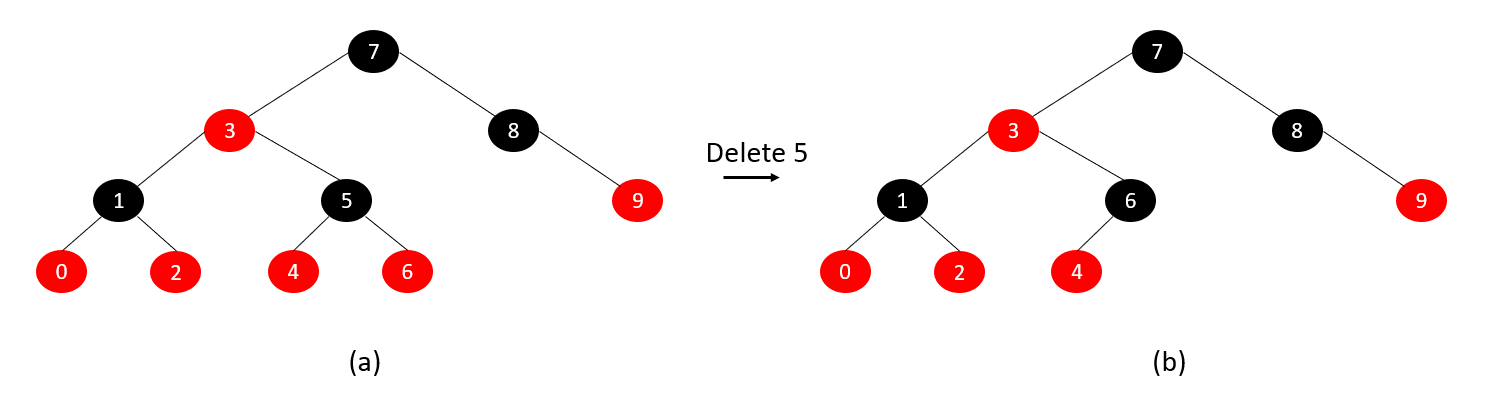
可绘制出生成的红黑树如下图(a)所示，删除关键字5之后的红黑树如图(b)所示：