1.1.1 向量

均值向量

互相关矩阵
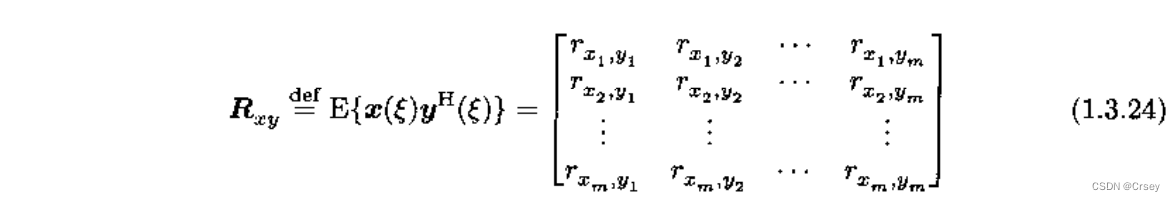
若互相关矩阵等于零矩阵,两个随机变量正交。
互协方差矩阵
互协方差函数越大,则两个随机信号的相关程度越强;反之,相关程度越弱。
若互协方差矩阵等于零矩阵,两个随机变量统计不相关。
对于分别具有零均值的两个随机变量,互协方差矩阵等于互相关矩阵,它们之间的统计不相关与正交是等价的。
相关函数

如果相关函数越接近0,两个随机变量的相似度越弱;如果相关函数越接近于1,则相似度越强。
1.1.2 矩阵的基本运算
复共轭矩阵

共轭转置又叫Hermitian伴随、Hermitian转置或Hermitian共轭。
加法交换律 A+B=B=A
加法结合律 (A+B)+C=A+(B+C)
乘法结合律 A(BC)=(AB)C
乘法左分配律 (A+B)C=AC+BC
乘法右分配律 A(B+C)=AB+AC

1.1.3 非奇异矩阵
(1) 一个n×n矩阵A是非奇异的,当且仅当Ax=0只有零解x=0
(2) 一个n×n矩阵A是非奇异的,当且仅当它的n个列向量线性无关。
1.4.1 向量的内积与范数
内积

外积(叉积)
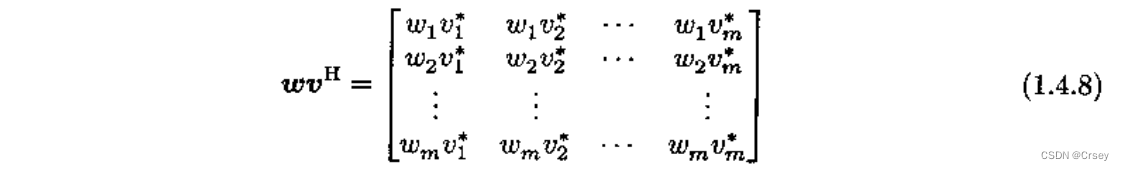
内积公理

范数公理

范数的一般性质


常用的向量范数

相似度
Euclidean距离(Nearest Neighbor Classification)

Mahalanobis距离

1.6.1 矩阵的二次型

1.6.2 矩阵的迹
n×n矩阵A的对角元素之和称为A的迹,记作tr(A)
关于迹的等式

关于迹的不等式

矩阵分析与应用 张贤达著








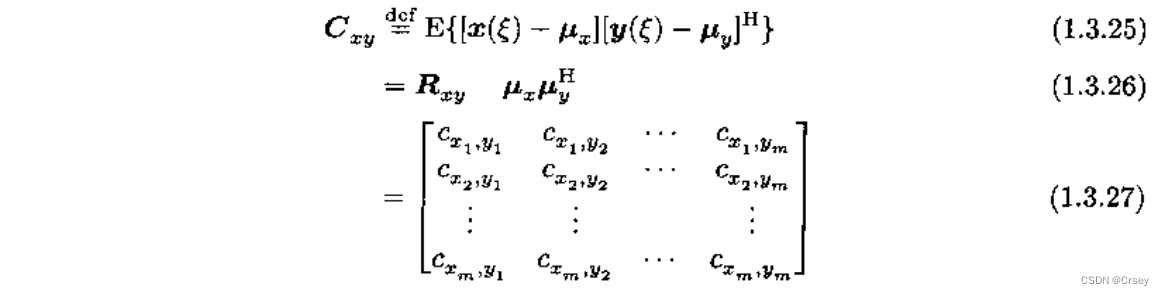

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








