IIR数字滤波器设计（模拟原型低通滤波器设计）

---

前言

前面介绍了IIR滤波器的设计流程，设计IIR数字滤波器需要先设计相应的模拟原型低通滤波器，这里将对巴特沃斯滤波器、切比雪夫滤波器及椭圆滤波器三种模拟原型低通滤波器的设计方法进行介绍。

---

一、 滤波器设计指标概述

假设模拟低通滤波器的技术指标表示如下：

• ${\omega }_p$：通带截止频率；
• ${\omega }_s$：阻带介质频率；
• ${\delta }_p$：通带波动；
• ${\delta }_s$：阻带波动。
  则通带最大衰减（dB）为：
  $$A_p=-20lg(1-{\delta }_p{)}^2\text{\hspace{1em}(1)}$$
  阻带最小衰减为：
  $$A_s=-20lg(1-{\delta }_s{)}^2\text{\hspace{1em}(2)}$$

模拟滤波器主要有巴特沃斯（Butterworth）滤波器、切比雪夫（Chebyshev）滤波器和椭圆滤波器三种类型。接下来将介绍这几种模拟低通滤波器的设计方法。

二、模拟低通滤波器设计

1. 巴特沃斯模拟低通滤波器设计

巴特沃斯模拟低通滤波器的频域响满足：
$$|H(j\omega ){|}^2=\frac{1}{1+(\omega /{\omega }_c{)}^{2N}}\text{\hspace{1em}(3)}$$

其中，$N$为滤波器阶数，${\omega }_c为3dB截止频率$

巴特沃斯模拟低通滤波器频域特性如下：

• $|H(j0)|=1,|H(j\infty )|=0,A({\omega }_c)=-20lg\frac{1}{\sqrt{2}}\approx 3dB$；
• 幅频响应单调下降；
• 具有最大平坦性，即$|H(e^{j\omega }){|}^2$在 $\omega =0$点处$1$至$2N-1$阶导数为零。

Butterworth模拟滤波器在通带的频率响应曲线最平滑

巴特沃斯模拟低通滤波器设计步骤如下：

• 1）确定模拟低通滤波器的阶数 $N$
  $$N\ge \frac{lg(\frac{10^{0.1A_s}-1}{10^{0.1A_p}-1})}{2lg({\omega }_s/{\omega }_p)}\text{\hspace{1em}(4)}$$

  对巴特沃斯低通滤波器，
  $$A(\omega )=-10lg|H(j\omega ){|}^2=10lg[1+(\omega /{\omega }_c{)}^{2N}]\text{\hspace{1em}(5)}$$
  给定滤波器设计指标 $({\omega }_p,A_p)$和$({\omega }_s,A_s)$，则有
  $$\{\begin{array}{l}{A}_p=10lg[1+({\omega }_p/{\omega }_c{)}^{2N}]\\ A_s=10lg[1+({\omega }_s/{\omega }_c{)}^{2N}]\end{array}\text{\hspace{1em}(6)}$$
  $N$取正整数，所以$N$的值向上取整。结合式（6）可得 $N$ 的取值范围如式（4）所示。

• 2）确定模拟低通滤波器的3dB截止频率 ${\omega }_c$
  $$\frac{{\omega }_p}{(10^{0.1A_p}-1{)}^{\frac{1}{2N}}}\le {\omega }_c\le \frac{{\omega }_s}{(10^{0.1A_s}-1{)}^{\frac{1}{2N}}}\text{\hspace{1em}(7)}$$

  同样，${\omega }_c$的取值范围也可以通过式（5）得到。$N$一般是向上取整得到的值，因此 ${\omega }_c$ 一般不是一个固定值，而是在一个范围内进行取值。(下图展示了 ${\omega }_c$ 取值情况不同时对滤波器过度带的影响)

  

• 3）确定模拟低通滤波器系统函数的极点
  $$s_k={\omega }_c{e}^{j\pi (\frac{1}{2}+\frac{2k-1}{2N})},k=1,2,\cdots ,N\text{\hspace{1em}(8)}$$

  实系数模拟系统的频率响应具有共轭对称性，即
  $$|H(j\omega ){|}^2=H(j\omega )H^{\ast }(j\omega )=H(j\omega )H(-j\omega )=H(s)H(-s){|}_{s=j\omega }\text{\hspace{1em}(9)}$$
  根据式（3）和式（9），可以求得系统函数的极点 $s_k$（位于s左半平面）。

• 4）确定模拟低通滤波器的系统函数 $H_L(s)$
  $$H_L(s)=\prod _{k=1}^N\frac{-s_k}{s-s_k}\text{\hspace{1em}(10)}$$

2. 切比雪夫模拟低通滤波器设计

切比雪夫滤波器分为切比雪夫Ⅰ型和切比雪夫Ⅱ型两种。切比雪夫Ⅰ型滤波器的幅频响应在通带内上下波动，在阻带内单调下降；切比雪夫Ⅱ型滤波器的幅频响应在通带内单调下降，在阻带内上下波动。这里对两种滤波器的设计分别进行介绍。

2.1 切比雪夫Ⅰ型模拟低通滤波器的设计

切比雪夫Ⅰ型模拟低通滤波器的频域响应满足：
$$|H(j\omega ){|}^2=\frac{1}{1+{\epsilon }^2{C}_N^2(\omega /{\omega }_c)}\text{\hspace{1em}(11)}$$

$N$：滤波器阶数；$\epsilon$：通带波纹；${\omega }_c$：通带截止频率；
$$C_N(x)=\{\begin{array}{l}cos[Narccos(x)]|x|\le 1\\ cosh[Narccosh(x)]|x|>1\end{array}\text{\hspace{1em}(12)}$$

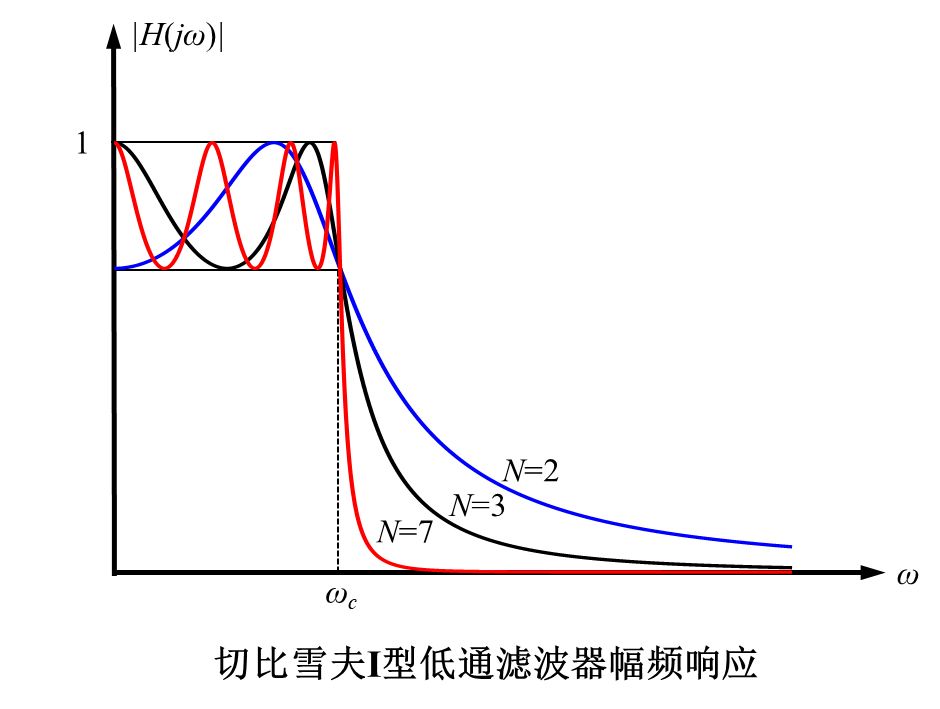
切比雪夫Ⅰ型模拟低通滤波器的频域特性如下：

• $0\le \omega \le {\omega }_c$时，$|H(j\omega ){|}^2$在 $1$ 和 $\frac{1}{1+{\epsilon }^2}$间等幅振荡；
• $\omega \ge {\omega }_c$时，$|H(j\omega ){|}^2$单调下降（N越大，下降越快）；
• $|H(j\omega ){|}^2$在 $\omega =0$时的值为：$|H(j0){|}^2=\{\begin{array}{l}1,N为奇数\\ 1/(1+{\epsilon }^2),N为偶数\end{array}$

切比雪夫Ⅰ型模拟低通滤波设计步骤如下：

• 1）通过通带截止频率 ${\omega }_p$ 确定 ${\omega }_c$
  $${\omega }_c={\omega }_p\text{\hspace{1em}(13)}$$
• 2）通过通带衰减 $A_p$ 确定 $\epsilon$
  $$\epsilon =\sqrt{10^{0.1A_p}-1}\text{\hspace{1em}(14)}$$

  对切比雪夫Ⅰ型低通滤波器，
  $$A(\omega )=-10lg|H(j\omega ){|}^2=10lg[1+{\epsilon }^2{C}_N^2(\omega /{\omega }_c)]\text{\hspace{1em}(15)}$$
  ${\omega }_c={\omega }_p$时， $A_p=10lg(1+{\epsilon }^2)$，所以 $\epsilon =\sqrt{10^{0.1A_p}-1}$。

• 3）通过滤波器通带、阻带指标确定滤波器阶数 $N$
  $$N\ge \frac{arccosh(\frac{1}{\epsilon }\sqrt{10^{0.1A_s}-1})}{arccosh({\omega }_s/{\omega }_p)}\text{\hspace{1em}(16)}$$

  ${\omega }_s$ 为阻带截止频率，$A_s$ 是阻带最小衰减。在 $\omega ={\omega }_s$ 、${\omega }_c={\omega }_p$时 可得 ：
  $$A_s=-10lg\frac{1}{1+{\epsilon }^2{C}_N^2({\omega }_s/{\omega }_p)}\text{\hspace{1em}(17)}$$
  求解可以得到式（16），$N$ 向上取整。

• 4）通过 $|H(j\omega ){|}^2$ 求模拟低通滤波器的极点
  $$s_k={\sigma }_k+j{\omega }_k,k=1,2,\cdots ,N\text{\hspace{1em}(22)}$$
  其中， $\beta =\frac{1}{N}arcsinh(\frac{1}{\epsilon })$， ${\sigma }_k$、${\omega }_k$ 可以表示为：
  $$\{\begin{array}{l}{\sigma }_k=-sinh(\beta )sin\frac{(2k-1)\pi }{2N}\\ {\omega }_k=-cosh(\beta )cos\frac{(2k-1)\pi }{2N}\end{array}\text{\hspace{1em}(23)}$$
• 5）通过极点确定滤波器的系统函数 $H_L(s)$
  $$H_L(s)=\prod _{k=1}^N\frac{H_0}{s-s_k}\text{\hspace{1em}(24)}$$

2.2 切比雪夫Ⅱ型模拟低通滤波器的设计

切比雪夫Ⅱ型模拟低通滤波器的频域响应满足：
$$|H(j\omega ){|}^2=1-\frac{1}{1+{\epsilon }^2{C}_N^2({\omega }_c/\omega )}=\frac{{\epsilon }^2{C}_N^2({\omega }_c/\omega )}{1+{\epsilon }^2{C}_N^2({\omega }_c/\omega )}\text{\hspace{1em}(25)}$$

$N$：滤波器阶数；$\epsilon$：阻带波纹；${\omega }_c$：阻带截止频率；

切比雪夫Ⅱ型模拟低通滤波器的频域特性如下：

• $\omega \ge {\omega }_c$时，$0\le |H(j\omega ){|}^2\le \frac{{\epsilon }^2}{1+{\epsilon }^2}$；
• 对任意 $N$，${\omega }_c$ 和$\epsilon$ 大于零时，$H(j0)=1$；
• 在通带 $0\le \omega \le {\omega }_c$ 时，$|H(j\omega ){|}^2$ 单调下降。

切比雪夫Ⅱ型模拟低通滤波设计步骤如下：

• 1）通过阻带截止频率 ${\omega }_s$ 确定 ${\omega }_c$
  $${\omega }_c={\omega }_s\text{\hspace{1em}(26)}$$

• 2）通过阻带衰减 $A_s$ 确定 $\epsilon$
  $$\epsilon =\frac{1}{\sqrt{10^{0.1A_s}-1}}\text{\hspace{1em}(27)}$$

  对切比雪夫Ⅱ型低通滤波器，
  $$A(\omega )=-10lg|H(j\omega ){|}^2=10lg[1+\frac{1}{{\epsilon }^2{C}_N^2({\omega }_c/\omega )}]\text{\hspace{1em}(28)}$$
  ${\omega }_c={\omega }_s$时， $A_s=10lg(1+\frac{1}{{\epsilon }^2})$，所以 $\epsilon =\frac{1}{\sqrt{10^{0.1A_s}-1}}$。

• 3）通过滤波器通带、阻带指标确定滤波器阶数 $N$
  $$N\ge \frac{arccosh(\frac{1}{\epsilon \sqrt{10^{0.1A_p}-1}})}{arccosh({\omega }_s/{\omega }_p)}\text{\hspace{1em}(29)}$$

  ${\omega }_p$ 为通带截止频率，$A_p$ 是通带最大衰减。在 $\omega ={\omega }_p$ 、${\omega }_c={\omega }_s$ 时，
  $$A_p=10lg[1+\frac{1}{{\epsilon }^2{C}_N^2({\omega }_s/{\omega }_p)}]\text{\hspace{1em}(30)}$$
  求解可以得到式（29），$N$ 向上取整。

• 4）通过 $|H(j\omega ){|}^2$ 求模拟低通滤波器的极点
  $$s_k={\sigma }_k+j{\omega }_k,k=1,2,\cdots ,N\text{\hspace{1em}(31)}$$

• 5）通过极点确定滤波器的系统函数 $H_L(s)$
  $$H_L(s)=\prod _{k=1}^N\frac{H_0}{s-s_k}\text{\hspace{1em}(32)}$$

3. 椭圆模拟低通滤波器的设计

椭圆模拟低通滤波器的频域响应满足：
$$|H(j\omega ){|}^2=\frac{1}{1+{\epsilon }^2{R}_N^2(\omega /{\omega }_c)}\text{\hspace{1em}(33)}$$

其中，$R_N(x)$为 $N$ 阶雅可比椭圆函数。

椭圆模拟低通滤波器的频域特性如下：

• $|\omega |<{\omega }_p$时，$\frac{1}{1+{\epsilon }^2}\le |H(j\omega ){|}^2\le 1$
• $\frac{{\omega }_c}{k}\le |\omega |<\infty$时，$0\le |H(j\omega ){|}^2\le \frac{1}{1+(\epsilon /k_1{)}^2}$
• $|H(j0){|}^2=\{\begin{array}{l}1/(1+{\epsilon }^2),N为偶数\\ 1,N为奇数\end{array}$

椭圆模拟低通滤波器设计步骤如下：

• 1）通过通带截止频率 ${\omega }_p$ 确定 ${\omega }_c$
  $${\omega }_c={\omega }_p\text{\hspace{1em}(34)}$$
• 2）通过通带衰减 $A_p$ 确定 $\epsilon$
  $$\epsilon =\frac{1}{\sqrt{10^{0.1A_p}-1}}\text{\hspace{1em}(35)}$$
• 3）通过通带和阻带截止频率确定 $k$
  $$k=\frac{{\omega }_p}{{\omega }_s}\text{\hspace{1em}(36)}$$
• 4）通过阻带衰减 $A_s$ 确定 $k_1$
  $$k1=\frac{\epsilon }{\sqrt{10^{0.1A_s}-1}}\text{\hspace{1em}(37)}$$
• 5）确定滤波器阶数 $N$
  $$N=\frac{K(k)K(\sqrt{1-k_1^2})}{K(\sqrt{1-k^2})K(k_1)}\text{\hspace{1em}(38)}$$

  其中，$K(x)$ 是第一类完全椭圆积分：
  $$K(x)={\int }_0^{\pi /2}\frac{1}{\sqrt{1-x^{2}si{n}^2\theta }}d\theta \text{\hspace{1em}(39)}$$

• 6）根据以上参数确定滤波器系统函数 $H_L(s)$

4. 三种模拟滤波器特点对比

• 在相同设计指标下， 巴特沃斯滤波器的阶数最高，椭圆滤波器的阶数最低；
• 巴特沃斯滤波器最容易实现，椭圆滤波器最不易实现（椭圆滤波器系统函数的极点距离虚轴最近）；

  

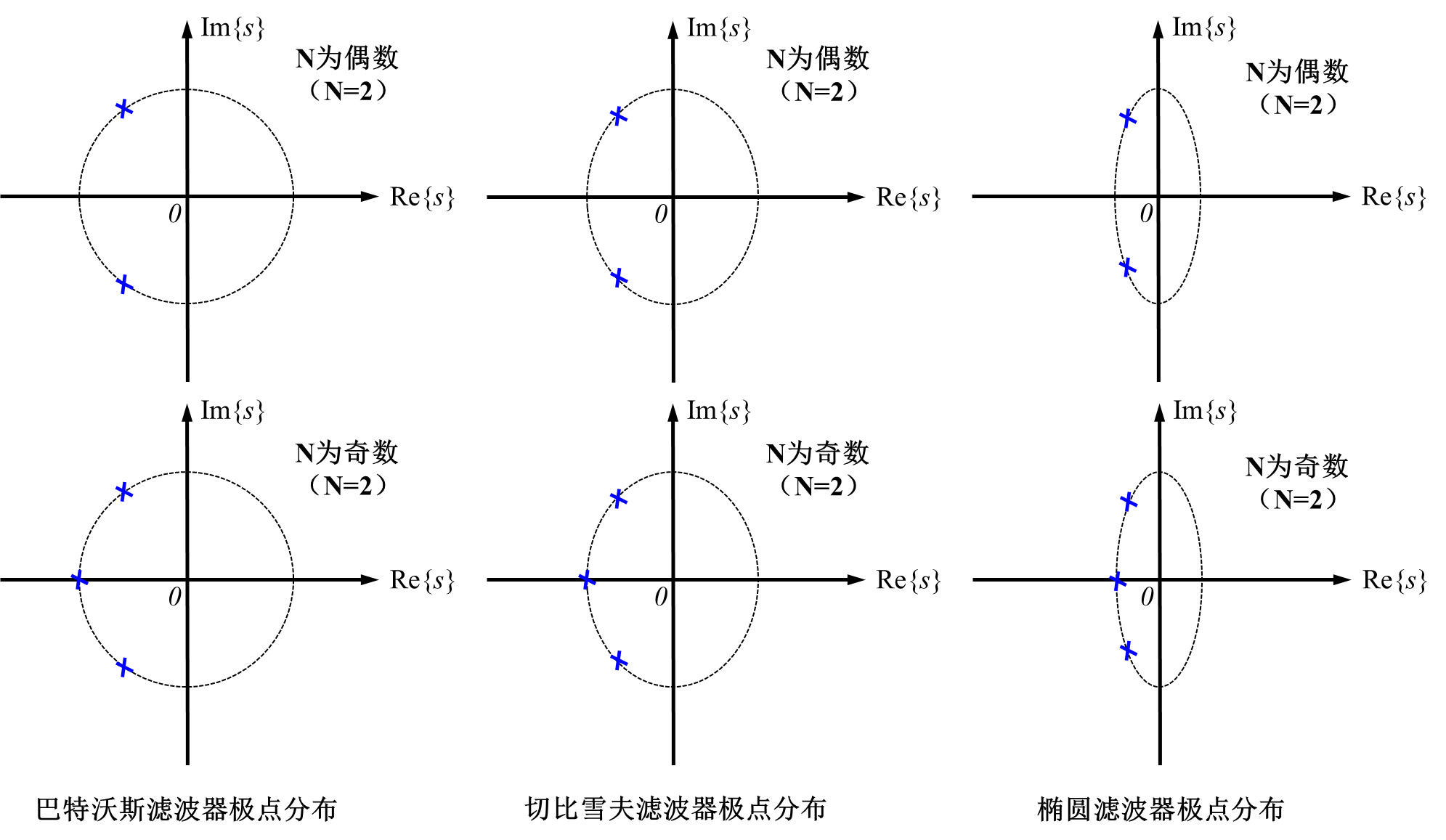
• 相同设计指标下，巴特沃斯滤波器的裕量最多，椭圆滤波器的裕量最少。

  

---

总结

模拟低通滤波器是设计IIR滤波器的基础，今天主要对巴特沃斯、切比雪夫及椭圆滤波器三种模拟滤波器进行了介绍，后续将介绍怎样通过模拟原型低通滤波器设计IIR数字滤波器。

参考资料

1. 刘纪红、孙宇舸、叶柠 等.数字信号处理原理与实践(修订版):电子信息学科基础课程系列教材[M].北京:清华大学出版社,2014.
2. 美 Proakis John G,美 Manolakis Dimitris G.数字信号处理:原理,算法与应用[M].电子工业出版社,2004.
3. 【数字信号处理(北京交通大学 陈后金)-哔哩哔哩】 https://b23.tv/cCBgSrV