一、排序算法
二、二分
三、高精度
四、前缀
五、差分
六、位运算
七、双指针算法
八、离散化
九、区间合并
一、排序算法
(一)快速排序算法
时间复杂度:最好O(nlog₂n) 平均O(nlog₂n) 最差O(n²)
空间复杂度:O(log₂n)
具有稳定性
主要思想是分治
1、首先找到枢纽元素pivot,一般取左边界元素
2、指定指针i为左边界,指针j为右边界,分别向右向左遍历扫描,如果满足q[i]>pivot且q[j]<pivot,交换q[i]和q[j]元素,此步操作为了保证在pivot元素左边的值必须小于等于pivot,处于pivot右边的元素必须大于等于pivot。直到不满足i<j
3、递归处理pivot的左右两边
模板:
void Quicksort(int* q, int l, int r)
{
if (l >= r) return;
int pivot = q[l], i = l - 1, j = r + 1;
while(i < j)
{
do i++; while(q[i] < pivot);
do j--; while(q[j] > pivot);
if(i < j) swap(q[i], q[j]);
}
/*
这里需要注意,如果使用i作为中间索引的话,则上面pivot的取值不能取q[l],否则会出现死循环,即:
Quicksort(q, l, i);
Quicksort(q, i - 1, r);
*/
Quicksort(q, l, j);
Quicksort(q, j + 1, r);
}
(二)归并排序算法
时间复杂度:最好O(nlog₂n) 平均O(nlog₂n) 最差O(nlog₂n)
空间复杂度:O(n)
具有稳定性,且稳定性最好
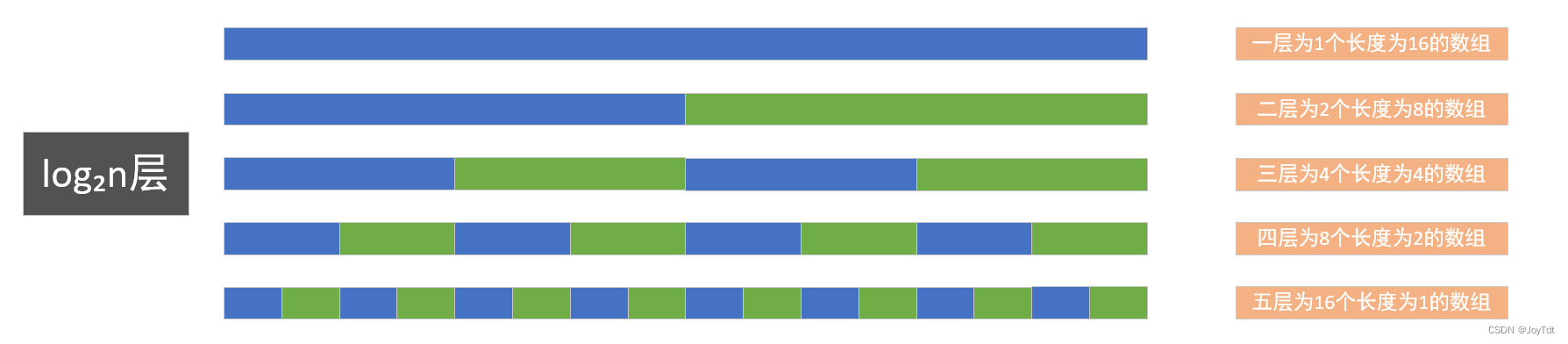
分析:
1.数组长度是n
2.第二层分成2个n/2的数组—————时间复杂度是2O(n/2)=O(N)
3.第三层分成4个n/4的数组—————时间复杂度是4O(n/4)=O(N)
4.要将n最后分治成n个长度为1的数组,共需要log₂n次。也就是第log₂n层,所以归并的时间复杂度是log₂n层乘以每一层O(n)的复杂度,结果是n*log₂n
核心:这个总体思路是分治,先把问题一分在分,不停的递归调用自身,来降低问体规模,但这会造成问题就是合并对时候会非常费劲!
降低规模-递归调用-合并数据
步骤:
1、确定分界点:mid = (l + r) /2
2、递归排序left和right
3、归并排序,合二为一,将两个有序序列合成一个序列,放在新数组temp中
4、复制temp数组到对应原数组的对应位置
模板:
void mergesort(int* q, int l, int r) //归并排序
{
if (l >= r) return;
int mid = (l + r) >> 1;
mergesort(q, l, mid);
mergesort(q, mid + 1, r);
// 到此已经排好mid左边和右边各自内部的顺序了
int k = 0, i = l, j = mid + 1;
int* temp = new int[r - l + 1];
while (i <= mid && j <= r)
{
if(q[i] <= q[j]) temp[k++] = q[i++];
else temp[k++] = q[j++];
}
while (i <= mid) temp[k++] = q[i++];
while (j <= r) temp[k++] = q[j++];
for (i = l, j = 0; i <= r; i++, j++) q[i] = temp[j];
}
二、二分
在数组中查找x的索引位置(前提有序):
1、将要查找值x与数组中间值mid相比较;
2、如果x=mid,则找到x,退出程序;
3、如果x<mid,则将边界设为[left,mid];
4、如果x>mid,则将边界设为[mid+1,right];
5、循环执行3,4两步骤,若直到数组长度为1,还没找到x,则数组中不存在x。如果找到x,则l就是x的位置;
* 注意每次二分会把答案区间缩小一半,且区间里一定有答案

需要注意if
check(mid)为true时,如果正确答案在mid的右侧,即要使l = mid,此时上面mid的取值为mid = (l + r + 1) >> 1;
check(mid)为true时,如果正确答案在mid的左侧,即要使r = mid,此时上面mid的取值为mid = (l + r) >> 1;
(一)整数二分算法
选择答案所在区域,确定使用哪个模板;其实目的就是寻找满足check条件的边界值x的索引位置
时时刻刻要保证答案(x的索引位置)在区间内,当这个区间长度为1时,则认为找到了答案
模板:
bool check(int x) {/* ... */} // 检查x是否满足某种性质
// 区间[l, r]被划分成[l, mid]和[mid + 1, r]时使用:
int bsearch_1(int l, int r)
{
while (l < r)
{
int mid = l + r >> 1;
if (check(mid)) r = mid; // check()判断mid是否满足性质
else l = mid + 1;
}
return l;
}
// 区间[l, r]被划分成[l, mid - 1]和[mid, r]时使用:注意l = mid和r = mid - 1时候对应mid = l + r + 1
int bsearch_2(int l, int r)
{
while (l < r)
{
int mid = l + r + 1 >> 1;
if (check(mid)) l = mid;
else r = mid - 1;
}
return l;
}
例子:

#include <bits/stdc++.h>
using namespace std;
const int N = 100010;
int n, m;
int q[];
int main()
{
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++)
{
scanf("%d", &q[i]);
}
while(m--)
{
int x;
scanf("%d", &x);
int l = 0, r = n - 1;
//找符合条件的左边界l
while(l < r)
{
int mid = (l + r) >> 1;
if(q[mid] >= x) r = mid;
else l = mid + 1;
}
if(q[l] != x) cout << "-1 -1" << endl;
else
{
cout << l << ' ';
int l = 0, r = n - 1;
//找符合条件的右边界l
while(l < r)
{
int mid = (l + r + 1) >> 1;
if(q[mid] <= x) l = mid;
else r = mid - 1;
}
cout << l << endl;
}
}
}
(二)浮点数二分算法
不需要像整数二分一样处理边界
时时刻刻要保证答案(x的索引位置)在区间内,当这个区间长度足够小的时候(小于1e-6时),则认为找到了答案
tips:如果题目要求保留4位小数,则eps的值取1e-6,5位小数则取1e-7,以此类推
bool check(double x) {/* ... */} // 检查x是否满足某种性质
double bsearch_3(double l, double r)
{
const double eps = 1e-6; // eps 表示精度,取决于题目对精度的要求
while (r - l > eps)
{
double mid = (l + r) / 2;
if (check(mid)) r = mid;
else l = mid;
}
return l;
}
例子:求输入x的开平方
//求输入x的开平方
#include<bits/stdc++.h>
using namespace std;
int main()
{
double x;
cin>>x;
double l = 0, r = x;
while(r - l > 1e-8)
{
double mid = (l + r) / 2;
if(mid * mid >= x) r = mid;
else l = mid; //不需要像整数二分一样处理边界
}
printf("%lf\n", l);
return 0;
}
三、高精度
存储方式:将大整数存到数组中,数组低位存大整数的低位,以此类推
比如数字为1234567,则新建一个vector A;将数字存入A中,A = [7, 6, 5, 4 ,3 ,2 ,1]
(一)高精度加法
原理:Ai+Bi+进位t,要求输入为两个数组(vector)
模板代码:
// C = A + B, A >= 0, B >= 0 默认要求A的size大于B的size
vector<int> add(vector<int> &A, vector<int> &B) //带引用是为了不影响本来的值
{
if (A.size() < B.size()) return add(B, A); //如若B大,则调用add(B, A)
vector<int> C; //存放的上一位的进位
int t = 0;
for (int i = 0; i < A.size(); i ++ )
{
t += A[i];
if (i < B.size()) t += B[i];
C.push_back(t % 10);
t /= 10;
}
if (t) C.push_back(t);
return C;
}
(二)高精度减法
手算模拟:

原理:要求输入为两个数组(vector)
模板代码:
//高精度减法
// C = A - B, 满足A >= B, A >= 0, B >= 0
vector<int> sub(vector<int> &A, vector<int> &B)
{
vector<int> C;
for (int i = 0, t = 0; i < A.size(); i ++ )
{
t = A[i] - t; //t上一位借位
if (i < B.size()) t -= B[i]; //只有B有这一位才需要减去
C.push_back((t + 10) % 10);
if (t < 0) t = 1; //如果t(t=Ai - Bi - t)的结果小于0,说明借位了,则令t = 1
else t = 0;
}
while (C.size() > 1 && C.back() == 0) C.pop_back();//去除vector中前面的0
return C;
}
(三)高精度乘低精度
手算模拟:

要求输入为高精度的整数(vector)和一个低精度的整数(int)
模板代码:
// C = A * b, A >= 0, b >= 0
vector<int> mul(vector<int> &A, int b)
{
vector<int> C;
int t = 0; //t存放进位
for (int i = 0; i < A.size() || t; i ++ )
{
if (i < A.size()) t += A[i] * b;
C.push_back(t % 10);
t /= 10;
}
while (C.size() > 1 && C.back() == 0) C.pop_back(); //去除前置0
return C;
}
(四)高精度除法
手动模拟:

要求输入为高精度的整数(vector)和一个低精度的整数(int),和一个余数r
模板代码:
//高精度整数除低精度整数 r为返回余数
// A / b = C ... r, A >= 0, b > 0
vector<int> div(vector<int> &A, int b, int &r)
{
vector<int> C;
r = 0;
for (int i = A.size() - 1; i >= 0; i -- ) //与乘法不同的是,这里从size-1开始算起
{
r = r * 10 + A[i];
C.push_back(r / b);
r %= b;
}
reverse(C.begin(), C.end());
while (C.size() > 1 && C.back() == 0) C.pop_back(); //去除前导0
return C;
}
四、前缀和
(一)前缀和(之前元素的和)
1、一维前缀和
原数组:a1 a2 a3 … an,要求下标从1开始,方便计S[0]为0
①前缀和作用:快速求出来一段数的和,比如在数组a中求[l , r]这一段元素的和,只需要求S[r] - S[l - 1],此时时间复杂度为O(1)
如果没有前缀和数组,则需要O(n)
②求前缀和(前n个数的和):Si = a1 + a2 + … + ai,S[0] = 0
模板代码:
S[i] = a[1] + a[2] + ... a[i]
a[l] + ... + a[r] = S[r] - S[l - 1]
2、二维前缀和

模板:
S[i, j] = 第i行j列格子左上部分所有元素的和
以(x1, y1)为左上角,(x2, y2)为右下角的子矩阵的和为:
S[x2, y2] - S[x1 - 1, y2] - S[x2, y1 - 1] + S[x1 - 1, y1 - 1]
小技巧:数据输入如果大于100万的话,建议使用scanf,否则使用cin
五、差分(当前元素减上一个元素)
分析:差分和前缀和互为逆运算(类似于积分和求导,重点理解非常巧妙),所以可以得出一个结论,对一个数组A的差分数组B,求两次前缀和操作,那么就会得到原数组A的前缀和数组C。
前提:若a[n]是b[n]的前缀和,则b[n]是a[n]的差分。
原数组:a1 , a2 , a3 , a4 , a5 , a6 … an;
构造数组: b1 , b2 , b3 , b4 , b5 , b6 … bn; 也叫差分数组
使得:an = b1 + b2 + b3 + b4 + … bn;
b称为a的差分,a称为b的前缀和;
b1 = a1;
b2 = a2 - a1;
b3 = a3 - a2;
…
bn = an - an-1;
所以如果给bl + c,那么就意味着给al之后的所有元素全部加上了个c,因为求a[i]的时候要用到b[1]到b[i]。
问题:给a数组在[l, r]之前的数全部加C
解决:
①使用for循环来加,那么时间复杂度就是O(n)
②使用差分的方法,则只用给b[l] + c和b[r] - c,时间复杂度为O(1),然后对b数组求前缀和,就可以求出更改后的a数组了
b[l] + c是给a[l]后面的元素所有都加上c,b[r] - c是给a[r]后面所有的都减c。这样就可以实现给从l到r之间的所有a数组的元素加c的操作了,而且时间复杂度是O(1)。
(一)一维差分
模板:
A是原数组,B是A的差分数组。即满足A[i] = B[i] + B[i-1] + ... + B[1]。A是B的前缀和数组
给区间[l, r]中的每个数加上c:共两个操作
一、B[l] += c
二、B[r + 1] -= c
(二)二维差分
模板:
给以(x1, y1)为左上角,(x2, y2)为右下角的子矩阵中的所有元素加上c:
S[x1, y1] += c, S[x2 + 1, y1] -= c, S[x1, y2 + 1] -= c, S[x2 + 1, y2 + 1] += c
六、位运算
//求n的第k位数字:
n >> k & 1
//返回n的最后一位1所代表的的整数:
lowbit(n) = n & -n //-n是给n安慰取反+1
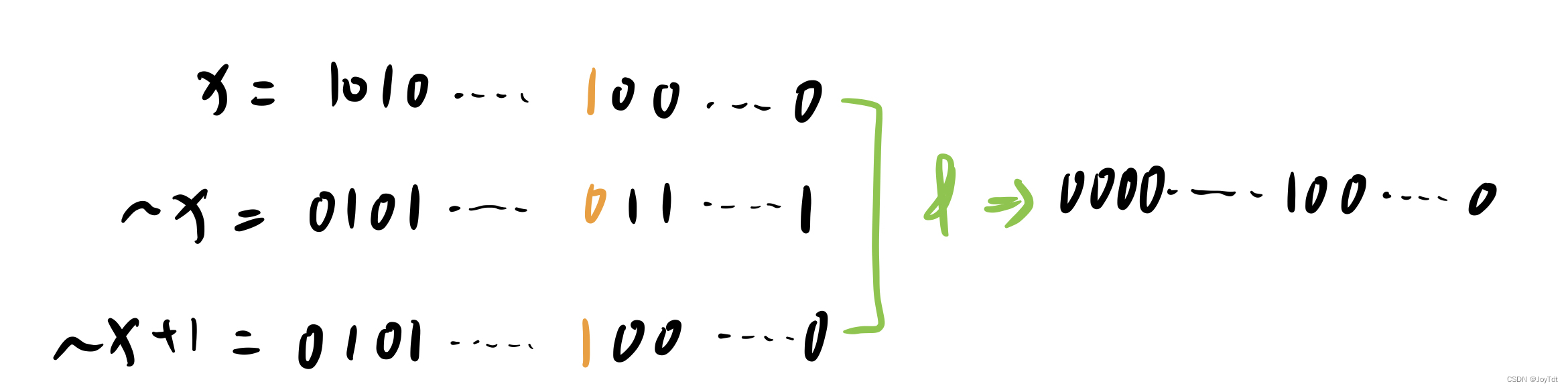
例子:801.二进制中1的个数
题目描述
给定一个长度为n的数列,请你求出数列中每个数的二进制表示中1的个数。
输入格式
第一行包含整数n。
第二行包含n个整数,表示整个数列。
输出格式
共一行,包含n个整数,其中的第i个数表示数列中的第i个数的二进制表示中1的个数
数据范围
1 < n < 100000.
0<数列中元素的值 < 10^9
输入样式:
5
1 2 3 4 5
输出 样式:
1 1 2 1 2
代码:
#include <iostream>
using namespace std;
int lowbit(int x)
{
return x & -x;
}
int main()
{
int n;
cin >> n;
while (n-- )
{
int x;
cin >> x;
int res = 0;
while (x)
{
x -= lowbit(x); //每次减去x的最后一位1对应的整数
res ++;
}
cout << res << endl;
}
}
七、双指针算法

暴力做法:时间复杂度O(n²)
for(int i = 0; i < n; i++)
for(int j = 0; j <= n; j++)
if(check(j, i))
{
res = max(res, i - j + 1);
}
核心逻辑:实际上在暴力算法的基础上,观察对应题目指针i和j移动时候的性质,尽量减少某一个指针的移动次数,来减少时间复杂度,从而提高性能。
下面是模板代码:
//双指针算法:O(n)
for(int i = 0, j = 0; i < n; i++)
{
while(j <= i && check(j, i)) j++;
res = max(res, i - j + 1);
// 具体问题的逻辑
}
常见问题分类:
(1) 对于一个序列,用两个指针维护一段区间
(2) 对于两个序列,维护某种次序,比如归并排序中合并两个有序序列的操作
双指针例子1:
#include<bits/stdc++.h>
using namespace std;
/*
input:
abc def ghi
output:
abc
def
ghi
*/
int main()
{
char str[1000];
gets(str);
int n = strlen(str);
for(int i = 0; i < n; i++)
{
int j = i;
while(j < n && str[j] != ' ') j++;
//这道题的具体逻辑
for(int k = i; k < j; k++) cout << str[k];
cout<<endl;
i = j;
}
return 0;
}
双指针例子2:799.最长连续不重复子序列
题目描述
给定一个长度为n的整数序列,请找出最长的不包含重复数字的连续子序列,输出它的长度。
输入格式
第一行包含整数n。
第二行包含n个整数(均在0~100000范围内),表示整数序列。
输出格式
共一行,包含一个整数,表示最长的不包含重复数字的连续子序列的长度。
数据范围
1 < n < 100000
输入样式:
5
1 2 2 3 5
输出样式:
3
#include<bits/stdc++.h>
using namespace std;
/*
*/
const int N = 100010;
int n;
int a[N], S[N];
int main()
{
cin >> n;
for(int i = 0; i < n; i++) cin >> a[i];
memset(S, 0, sizeof S); // 初始化S数组
int res = 0;
for(int i = 0, j = 0; i < n; i++)
{
S[a[i]] ++;
while (S[a[i]] > 1)
{
S[a[j]] --;
j++;
}
res = max(res, i - j + 1);
}
cout << res << endl;
return 0;
}
八、离散化
特用于数据大小范围非常广,但是数据分布非常稀疏,此时将需要用到的数据,离散化到一个小一点的向量或者数组中,来实现省空间和时间。如若出现重复元素,需要去重,还需要排序。- 用到前缀和求区间内值的和。
- 去重:先将数组进行排序,利用unique,erase去重。
- 二分查找。
模板代码:
vector<int> alls; // 存储所有待离散化的值
sort(alls.begin(), alls.end()); // 将所有值排序
alls.erase(unique(alls.begin(), alls.end()), alls.end()); // 去掉重复元素
// 二分求出x对应的离散化的值
int find(int x) // 找到第一个大于等于x的位置
{
int l = 0, r = alls.size() - 1;
while (l < r)
{
int mid = l + r >> 1;
if (alls[mid] >= x) r = mid;
else l = mid + 1;
}
return r + 1; // 映射到1, 2, ...n
}
题目:802.区间和
题目描述
假定有一个无限长的数轴,数轴上每个坐标上的数都是0。
现在,我们首先进行 n 次操作,每次操作将某一位置x上的数加c。
近下来,进行 m 次询问,每个询问包含两个整数l和r,你需要求出在区间的所有数的和.
输入格式
第一行包含两个整数n和m。
接下来 n 行,每行包含两个整数x和c。
再接下里 m 行,每行包含两个整数I和r。
输出格式
共m行,每行输出一个询问中所求的区间内数字和。
数据范围
-10^9 <= x <= 10^9
1 <= n,m <= 10^5
-10^9 <= l <= r <= 10^9
-10000 <= c <= 10000
输入样式:
3 3
1 2
3 6
7 5
1 3
4 6
7 8
输出样式:
8
0
5
分析:如果所有的数范围比较小,可以直接用前缀和处理
核心:把n个要操作的数x1 x2 … xn,放到alls数组中,并排序去重。然后分别将每个x都能唯一映射到0~alls.size()-1中的每一个索引,然后通过索引来访问对应x的值,而索引大小也反应了x的大小(因为是排好序去重后的)
code:
#include<bits/stdc++.h>
using namespace std;
typedef pair<int, int> PII;
const int N = 300010; //插入操作最多10w,查询操作每组需要两个,最多10w组,所以需要开30w的空间
int n, m;
int a[N], s[N]; //a是数据数组,s是前缀和数组
vector<int> alls; //待离散化的数组,里面存放的是要操作的数据
vector<PII> add, query; //add是待操作加法的向量,元素是两个int<int, int>,query是待查询的向量
/**
* @function :使用二分法,实现真实数 x 和离散化后的索引值的映射
* x 是需要操作的数,然后我们需要在(排好序,去重后的alls数组)中使用二分找到第一个大于x的值的索引序号
*/
int find(int x) // 找到第一个大于等于x的位置
{
int l = 0, r = alls.size() - 1;
while (l < r)
{
int mid = l + r >> 1;
if (alls[mid] >= x) r = mid;
else l = mid + 1;
}
return r + 1; // 映射到1, 2, ...n
}
/*
分析:
如果数据范围比较小的时候,可以直接用前缀和。
此时将用到的数据离散化(映射)成较小的数组然后在计算
*/
int main()
{
cin >> n >> m;
for(int i = 0; i < n; i++)
{
int x, c;
cin >> x >> c;
add.push_back({x, c});
alls.push_back({x});
}
for (int i = 0; i < m; i++)
{
int l, r;
cin >> l >> r;
query.push_back({l, r});
alls.push_back(l);
alls.push_back(r);
}
//排序 + 去重
sort(alls.begin(), alls.end()); // 将所有要操作的值排序
alls.erase(unique(alls.begin(), alls.end()), alls.end()); // 去掉重复元素
//处理插入
for(auto item1 : add)
{
int x = find(item1.first); //找到item.first离散化之后的索引
a[x] += item1.second;
}
//预处理前缀和——方便计算区间和
for(int i = 1; i <= alls.size(); i++)
{
s[i] = s[i - 1] + a[i];
}
//处理询问
for(auto item1 : query)
{
int l = find(item1.first), r = find(item1.second);
cout << s[r] - s[l - 1] << endl;
}
return 0;
}
九、区间合并
803.区间合并

题目描述
给定n个区间[l,r],要求合并所有有交集的区间。注意如果在端点处相交,也算有交集。输出合并完成后的区间个数。
例如:[1,3]和[2,6]可以合并为一个区间[1,6]。

核心思想:
1、按区间左端点排序
2、初始化左右端点。左为start,右为end,边界为-2e9到-2e9(取负无穷到负无穷)
3、比较维护区间的end与待加入区间的左端点,如果两个区间有交集,则更新维护区间为当前区间和待加入区间的并集,并将更新后的区间记录下来。
4、返回数组长度。
输入格式
第一行包含整数n。
接下来n行,每行包含两个整数l和r。
输出格式
共—行,包含一个整数,表示合并区间完成后的区间个数。
数据范围
1 < n < 100000
-10^9 < l < r <10^9
输入样式:
5
1 2
2 4
5 6
7 8
7 9
输出样式:
3
代码:
#include<bits/stdc++.h>
using namespace std;
typedef pair<int, int> PII; //first存储区间左端点,second存区间的右端点
const int N = 100010;
int n;
vector<PII> segs;
// 将所有存在交集的区间合并———————————核心代码部分
void merge(vector<PII> &segs)
{
vector<PII> res;
sort(segs.begin(), segs.end()); //sort排序规则先按照左端点排序,在按照右端点排序
int st = -2e9, ed = -2e9; // 维护区间的左右端点初始化
for (auto seg : segs)
{
if (ed < seg.first) //如果维护区间的右端点在待合并区间的左端点的左边,也就是两区间没有重合部分,则push维护区间到结果res中,并且更新维护区间的st和ed为当前新区间的左右端点。
{
if (st != -2e9) res.push_back({st, ed}); // 如果不是初试状态,直接存入结果res中
st = seg.first, ed = seg.second; // 更新左边界和右边界
}
else ed = max(ed, seg.second); // 否则说明,两个区间有重合部分,更新维护区间的右端点ed为大的那一个右边界
}
if (st != -2e9) res.push_back({st, ed});
segs = res;
}
int main()
{
cin >> n;
for( int i = 0; i < n; i++ )
{
int l, r;
cin >> l >> r;
segs.push_back({l, r});
}
merge(segs);
cout << segs.size() << endl;
return 0;
}





















 9020
9020











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








