房价影响因素挖掘

作业要求：

1、数据清洗、整合

要求：
①将“house_rent”、“house_sell”分别读取
②分别计算平方米建筑面积的月租金、每平方米建筑面积的房价
③将数据按照小区名合并

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings('ignore')
import os
os.chdir('C:/Users/Administrator/Desktop/项目10房价影响因素挖掘')

df_rent = pd.read_csv('house_rent.csv',engine='python')
df_sell = pd.read_csv('house_sell.csv',engine='python')

#删除缺失值
df_rent.dropna(inplace=True)
df_sell.dropna(inplace=True)

#计算每平米建筑面积的月租金
df_rent['rent_area'] = df_rent['price']/df_rent['area']
#按照小区做均值分析
data_rent = df_rent[['community','rent_area','lng','lat']].groupby(by='community').mean()
data_sell = df_sell[['property_name','average_price','lng','lat']].groupby(by='property_name').mean()
data_rent.reset_index(inplace=True)
data_sell.reset_index(inplace=True)

#合并数据
data = pd.merge(data_rent,data_sell,left_on='community',right_on='property_name')
data = data[['community','rent_area','average_price','lng_x','lat_x']]
data = data.rename(columns = {'average_price':'sell_area','lng_x':'lng','lat_x':'lat'})

2、计算“房屋售租比”，并做初步判断

要求：
① 计算指标
② 绘制直方图、箱型图看“售租比”的一个数据分布情况
提示：
① “房屋售租比”=“每平方米建筑面积的房价”/“每平方米建筑面积的月租金”
② 直方图bins数量大于80来作图
** 一个房子，100平，2万单价 → 2000000万，首付600000,贷款1400000
** 租金 8800，20000/（8800/100）

#计算房屋售租比
data['sell_rent'] = data['sell_area'] / data['rent_area']
print('上海房屋租售比的中位数为%i个月' % data['sell_rent'].median())

#绘制直方图
data['sell_rent'].plot.hist(bins=100,stacked=True,color='green',
    alpha=0.6,grid=True,figsize=(10,4),edgecolor='black')
plt.title('房屋售租比-直方图')

#绘制箱型图
color = dict(boxes='DarkGreen',whiskers='DarkOrange',medians='DarkBlue',caps='Gray')
#boxes:箱线
#whiskers：分位数与error bar横线之间竖线的颜色
#medians：中位数线的颜色
#caps：error bar横线颜色
data['sell_rent'].plot.box(vert=False,grid=True,color=color,figsize=(10,4))
plt.title('房屋售租比-箱型图')

3、上海市人口密度、路网密度、餐饮价格和“房屋每平米均价”是否有关系呢？

要求：
① 首先，导出整理好的数据，并qgis中绘制空间格网图，查看房屋每平米均价、房屋每平米租金及售租比数据的空间分布
② 第二，空间统计，分别按照格网对人口密度、路网密度、餐饮价格进行指标统计并标准化
③ 第三，加载上海中心点point空间数据，计算每个网格到市中心距离
④ 第四，将空间格网的“房屋每平米均价”按照距市中心的距离排序，并制作散点图，看看能否挖掘出什么信息
*** 这里市中心点坐标为：lng-353508.848122，lat-3456140.926976 (投影坐标系)

空间分析步骤：
1.加载数据net_population.shp,cy.shp,road.shp
2.加载文件data.csv,另存为datapoint.shp
3.计算线条总长，输出shape文件net01
4.输入多边形矢量net01，输入点矢量图层cy,输入要聚合的矢量点图层属性-人均消费，采用均值统计方法，计算多边形内点的数目，输出shape文件net02
5.输入多边形矢量net02，输入点矢量图层datapoint，输入要聚合的矢量点图层，计算多边形内点的数目，输出shape文件net03

导出整理好的数据：

data.to_csv('data.csv')

data3 = pd.read_csv('result.csv',engine='python')
data3.fillna(0,inplace=True)

#创建函数进行指标统计并标准化
def f1(data,col):
    return (data[col]-data[col].min())/(data[col].max()-data[col].min())

data3['人口密度指标'] = f1(data3,'Z')
data3['路网密度指标'] = f1(data3,'长度')
data3['餐饮价格指标'] = f1(data3,'人均消费_')

#计算离市中心距离
data3['离市中心距离'] = ((data3['lng']-353508.848122)**2+(data3['lat']-3456140.926976)**2)**0.5
data3_test = data3[['人口密度指标','路网密度指标','餐饮价格指标','sell_area_','离市中心距离']]
#去除售租比为0的数据
data3_test = data3_test[data3_test['sell_area_']>0].reset_index()
del data3_test['index']

plt.figure(figsize=(10,4))
plt.scatter(data3_test['人口密度指标'],data3_test['sell_area_'],s=2,alpha=0.5)
plt.xlabel('人口密度指标')
plt.ylabel('房屋每平米均价')
plt.grid()

plt.figure(figsize=(10,4))
plt.scatter(data3_test['路网密度指标'],data3_test['sell_area_'],s=2,alpha=0.5)
plt.xlabel('路网密度指标')
plt.ylabel('房屋每平米均价')
plt.grid()

plt.figure(figsize=(10,4))
plt.scatter(data3_test['餐饮价格指标'],data3_test['sell_area_'],s=2,alpha=0.5)
plt.xlabel('餐饮价格指标')
plt.ylabel('房屋每平米均价')
plt.grid()

plt.figure(figsize=(10,4))
plt.scatter(data3_test['离市中心距离'],data3_test['sell_area_'],s=3,alpha=0.5,color='red')
plt.xlabel('离市中心距离')
plt.ylabel('房屋每平米均价')
plt.grid()

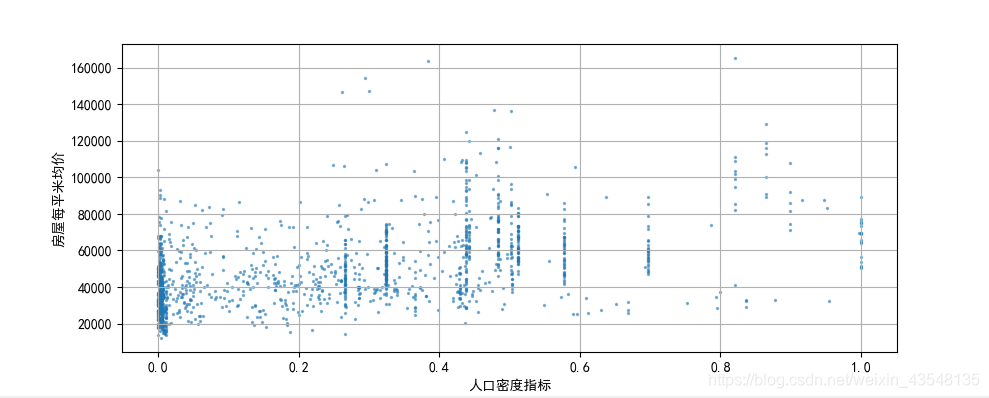
结论：

① 在上海全市层面，“离市中心距离”与“房屋每平米均价”相关性最强
② “人口密度”及“路网密度”和“房屋每平米均价”为中等相关
③ “餐饮价格”与“房屋每平米均价”为弱相关
④ “房屋每平米均价”数据的离散程度却和空间距离有关 → “房屋每平米均价”越靠近市中心越离散，越远离市中心则越收敛

4、按照离市中心距离每10km，分别再次判断人口密度、路网密度、餐饮价格和“房屋每平米均价”的相关程度

要求：
① 按照空间距离分别迭代计算三指标和“房屋每平米均价”的关系
② 绘制折线图查看：随着市中心距离增加，不同指标相关系系数变化情况
*** 建议用bokeh制图

data3_test.corr().loc['sell_area_']
人口密度指标        0.502724
路网密度指标        0.449742
餐饮价格指标        0.184749
sell_area_         1.000000
离市中心距离       -0.735211

dis = []
rkmd_person = []
lwmd_person = []
cyjg_person = []
zxjl_person = []

for distance in range(10000,70000,10000):
    datai = data3_test[data3_test['离市中心距离'] <= distance]
    r_value = datai.corr().loc['sell_area_']
    dis.append(distance)
    rkmd_person.append(r_value.loc['人口密度指标'])
    lwmd_person.append(r_value.loc['路网密度指标'])
    cyjg_person.append(r_value.loc['餐饮价格指标'])
    zxjl_person.append(r_value.loc['离市中心距离'])
    print('离市中心距离小于等于%i米时：' % distance)
    print('数据量为%i条' % len(datai))   
    print('人口密度指标相关性系数为%.3f' % r_value.loc['人口密度指标'])
    print('路网密度指标相关性系数为%.3f' % r_value.loc['路网密度指标'])
    print('餐饮价格指标相关性系数为%.3f' % r_value.loc['餐饮价格指标'])   
    print('离市中心距离相关性系数为%.3f' % r_value.loc['离市中心距离'])

离市中心距离小于等于10000米时：
数据量为294条
人口密度指标相关性系数为0.070
路网密度指标相关性系数为-0.091
餐饮价格指标相关性系数为0.125
离市中心距离相关性系数为-0.493

离市中心距离小于等于20000米时：
数据量为795条
人口密度指标相关性系数为0.371
路网密度指标相关性系数为0.195
餐饮价格指标相关性系数为0.160
离市中心距离相关性系数为-0.596

离市中心距离小于等于30000米时：
数据量为1133条
人口密度指标相关性系数为0.494
路网密度指标相关性系数为0.378
餐饮价格指标相关性系数为0.164
离市中心距离相关性系数为-0.713

离市中心距离小于等于40000米时：
数据量为1328条
人口密度指标相关性系数为0.463
路网密度指标相关性系数为0.412
餐饮价格指标相关性系数为0.172
离市中心距离相关性系数为-0.731

离市中心距离小于等于50000米时：
数据量为1389条
人口密度指标相关性系数为0.490
路网密度指标相关性系数为0.441
餐饮价格指标相关性系数为0.184
离市中心距离相关性系数为-0.743

离市中心距离小于等于60000米时：
数据量为1431条
人口密度指标相关性系数为0.503
路网密度指标相关性系数为0.450
餐饮价格指标相关性系数为0.185
离市中心距离相关性系数为-0.735

df3_result = pd.DataFrame({'cyjg_person':cyjg_person,
                          'lwmd_person':lwmd_person,
                          'rkmd_person':rkmd_person,
                          'zxjl_person':zxjl_person},
                          index = dis)    
    
    
from bokeh.plotting import show,figure,output_file  
from bokeh.models import ColumnDataSource,HoverTool

source = ColumnDataSource(df3_result)

hover = HoverTool(tooltips = [('离市中心距离','@index'),
                              ('人口密度相关系数','@rkmd_person'),
                              ('路网密度相关系数','@lwmd_person'),
                              ('餐饮价格相关系数','@cyjg_person'),
                              ('中心距离相关系数','@zxjl_person')])
output_file('不同指标相关性系数变化情况.html')
p = figure(plot_width=800,plot_height=350,
         title = '随着市中心距离增加，不同指标相关性系数变化情况',
         tools = [hover,'box_select,reset,xwheel_zoom,pan,crosshair'])

p.line(x='index',y='rkmd_person',source=source,
       line_alpha=0.8,line_color='green',line_dash=[15,4],
       legend='人口密度相关系数')
p.circle(x='index',y='rkmd_person',source=source,
         size=8,color='green',alpha=0.8,
         legend='人口密度相关系数')

p.line(x='index',y='lwmd_person',source=source,
       line_alpha=0.8,line_color='blue',line_dash=[15,4],
       legend='路网密度相关系数')
p.circle(x='index',y='lwmd_person',source=source,
         size=8,color='blue',alpha=0.8,
         legend='路网密度相关系数')

p.line(x='index',y='cyjg_person',source=source,
       line_alpha=0.8,line_color='black',line_dash=[15,4],
       legend='餐饮价格相关系数')
p.circle(x='index',y='cyjg_person',source=source,
         size=8,color='black',alpha=0.8,
         legend='餐饮价格相关系数')

p.line(x='index',y='zxjl_person',source=source,
       line_alpha=0.8,line_color='red',line_dash=[15,4],
       legend='中心距离相关系数')
p.circle(x='index',y='zxjl_person',source=source,
         size=8,color='red',alpha=0.8,
         legend='中心距离相关系数')

p.legend.location = 'center_right'
show(p)

结论：

① “人口密度”、“道路密度”、“离市中心距离”和“房屋均价”有着明显的相关性，而“餐饮价格”和“房屋均价”相关性较弱
② 随着离市中心的距离越远，指标的相关性在数据上体现更明显，而这个分界线大概在20-30km处，这正是上海中心城区和郊区的分界 → 上海房价市场的“中心城区-郊区”分化特征
③ 中心城区的房产市场对指标因素的影响更加敏锐，而郊区则更迟钝 → 越靠近市中心，影响因素越复杂