【算法图解】——算法必备

最新推荐文章于 2022-12-10 15:51:17 发布

千里足行~始于足下

最新推荐文章于 2022-12-10 15:51:17 发布

阅读量854

点赞数 2

分类专栏：算法及数据结构

本文链接：https://blog.csdn.net/weixin_43585712/article/details/108482687

版权

算法及数据结构专栏收录该内容

16 篇文章 0 订阅

订阅专栏

1. 大O表示法

大O表示法： $O{(n)}$ ,n代表操作数，指出了算法在最坏情况下的速度有多快，因为我们不仅要知道算法运行完的时间，还需要知道运行时间如何随着数据的增长而增加。

比如：二分查找即折半查找，简单查找是一个一个的找，对于10个元素的有序列表，简单查找： $O{(10)}$ =10，折半查找： $O{(log 10)}$ =4，默认以2为底，那么从10000个找呢？两者的操作数10000，14，可见差别多大。
为什么操作数代表了时间呢？因为计算机执行一个操作（比如4则运算）的时间基本是一样的。

旅行商问题
有一位旅行商要前往5个城市，怎么去能确保路程最短呢？
如果去100个城市呢？
如果去5个城市， $A_5^{5}$ =120,计算每种情况的路程取最小。
如果去100个城市，下面用程序计算的 $A_{100}^{100}$

计算量太大了，城市增加了20倍，旅行选择却多了不止一个量级，这是一个 $O{(n!)}$ 最慢的算法。

2. 递归

基线条件：停止调用自己，避免形成无限循环。
递归条件：函数调用自己。
注：如果使用循环，程序的性能可能更高，如果使用递归，程序更容易理解。
在这里插入图片描述

2.1 调用栈(重要)

存储多个函数的变量，称为调用栈。

最后回到greet函数，没有其他事情可以做，于是就返回结果。

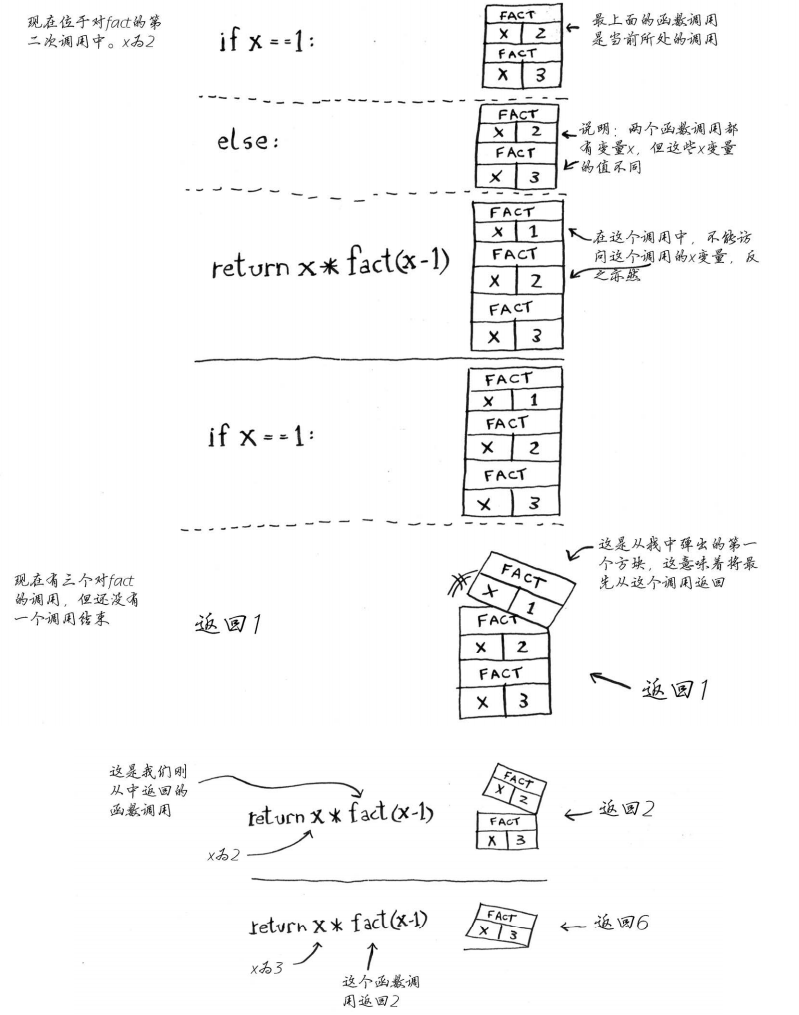
2.2 递归调用栈

每个fact都有自己的x变量,在一个函数调用中不能访问另一个函数的x变量。

3. 分而治之（D&C）

有时候，你会遇到使用任何已知算法都无法解决的问题，分而治之便是一种通用的方法之一,它也是递归式求解。

问题：如何均匀地划分一块地，使得分出的方块尽可能的大？
比如长宽为640，1680,依次划分，直到余下的那一块也可以均匀划分。

由上图知：最大的方块是80

D&C的工作原理：

1.找出简单的基线条件（直到余下的方块也可以均匀划分）
2.确定如何缩小问题的规模，使其符合基线条件（不断地找尽可能大的划分，下一次再对余下的做重复操作）
另一个典型的例子是快速排序：
快速排序的基线条件是只包含一个元素或者空数组，通过基点缩小问题的规模。具体参考链接：快速排序

在这里插入图片描述

4. 散列表

散列函数：将输入映射到数字。
散列表是根据散列函数返回索引并查到指定元素。
主要用途：

用于查找，比如查找某人的电话号码，姓名->索引->号码
防止重复，比如插入新名字时检查下是否已有该名字
用于网络缓存，谷歌搜索根据用户的习惯会缓存一些内容，等到用户再次查询时，以免服务器再通过处理来生成它们，直接在已有的缓存区查找。

冲突：如果你将苹果的价格存储第一个位置，却发现第一个位置是梨的价格，这样就会造成冲突。
解决冲突的方式：每一个位置放一个链表.

通过上图可以看到：散列表是数组和链表的结合，插入、删除时要判断是否有相同元素，所以最差的情况是 $O (n)$ ,最好的情况是空表，或者没有重复的。
查找时最好的情况是通过哈希函数返回索引，最差的是返回索引还要在链表中找，所以好的散列函数很重要。

5. 广度优先搜索算法

5.1 理论

广度优先搜索算法(Breadth First Search，BSF)，类似树的层次遍历，常用于求最短路径问题。
一句话：顺着起点撒网，先到先得。
基本思想是：

1.从图（有向和无向）中某顶点v出发，首先访问定点v
2.在访问了v之后依次访问v的各个未曾访问过的邻接点；
3.然后分别从这些邻接点出发依次访问它们的邻接点，并使得先被访问的顶点的邻接点先于后被访问的顶点的邻接点被访问;
4.直至图中所有已被访问的顶点的邻接点都被访问到;
5.如果此时图中尚有顶点未被访问，则需要另选一个未曾被访问过的顶点作为新的起始点，重复上述过程，直至图中所有顶点都被访问到为止。

5.2 python实现

利用队实现：复杂度O(V+E)

import queue as Qu
def bfs(adj, start):
    visited = set()#没有先后顺序的
    q = Qu.Queue()#创建一个队列
    q.put(start)
    while not q.empty():
        u = q.get()#先访问的邻接点先访问
        print(u)
        for v in adj.get(u, []):#找出u的相邻点，找不到的返回空列表
            if v not in visited:
                visited.add(v)
                q.put(v)
graph = {1: [4, 2,3], 2: [3, 4,5], 3: [4], 4: [5]}
bfs(graph, 1)#1，4，2，3，5

6. 深度优先搜索算法

6.1 理论：

图（有向和无向）的深度优先搜索(Depth First Search, DFS)，和树的前序遍历非常类似，应用待加？？？。
一句话：顺着起点往下走，直到无路可走。
基本思想是：

1.从顶点v出发，首先访问该顶点;
2.然后依次从它的各个未被访问的邻接点出发深度优先搜索遍历图;
3.直至图中所有和v有路径相通的顶点都被访问到。
4.若此时尚有其他顶点未被访问到，则另选一个未被访问的顶点作起始点，重复上述过程，直至图中所有顶点都被访问到为止。

6.1 python实现：

利用栈实现：复杂度O(V+E)

def dfs(adj, start):
    visited = set()#p判断哪些点访问到了
    stack = [[start, 0]]#stack代表第几个字典的键，0代表某个值的第1个元素
    print(start)
    while stack:        
        (v, next_child_idx) = stack[-1]
        if (v not in adj) or (next_child_idx >= len(adj[v])):
            #如果某个键没有，或者键值的长度越界了，说明走到底了
            stack.pop()
            continue
        next_child = adj[v][next_child_idx]
        stack[-1][1] += 1#键值访问到后加1
        if next_child in visited:
            continue
        print(next_child)
        visited.add(next_child)
        stack.append([next_child, 0])
graph = {1: [4, 2,3], 2: [3, 4,5], 3: [4], 4: [5]}
dfs(graph, 1)#1，4，5，2，3

7. 狄克斯特拉算法

7.1 理论：

算法只适用于权值为正的图，常用于求总权重最小的路径，如果图中包含负权边，请使用贝尔曼-福德算法（了解）。
算法步骤：
(1) 找出“最便宜”的节点，即可在最短时间内到达的节点。
(2) 更新该节点的邻居的开销，其含义将稍后介绍。
(3) 重复这个过程，直到对图中的每个节点都这样做了。
(4) 计算最终路径。
下面的图展示了广度优先搜索和狄克斯特拉算法的区别：

乐谱换钢琴的例子：

7.2 python实现

为了实现简单，我们以下面的为例：

# 用散列表实现图的关系
graph = {}
graph["start"] = {}
graph["start"]["a"] = 6
graph["start"]["b"] = 2
graph["a"] = {}
graph["a"]["end"] = 1
graph["b"] = {}
graph["b"]["a"] = 3
graph["b"]["end"] = 5
graph["end"] = {}
# 创建节点的开销表，开销是指从"起点"到该节点的权重
# 无穷大
infinity = float("inf")
costs = {}
costs["a"] = 6
costs["b"] = 2
costs["end"] = infinity

# 父节点散列表,键值是父节点
parents = {}
parents["a"] = "start"
parents["b"] = "start"
parents["end"] = None

# 已经处理过的节点，需要记录
processed = []
# 每次找到开销最小的节点
def find_lowest_cost_node(costs):
    # 初始化数据
    lowest_cost = infinity
    lowest_cost_node = None
    # 遍历所有节点
    for node in costs:
       # 如果当前节点的开销比已经存在的开销小且该节点没有被处理，则更新该节点为开销最小的节点
       if not node in processed and costs[node] < lowest_cost:
            lowest_cost = costs[node]
            lowest_cost_node = node
    return lowest_cost_node
# 为最终的结果找到最短路径
def find_shortest_path():
    node = "end"
    shortest_path = ["end"]
    while parents[node] != "start":
        shortest_path.append(parents[node])
        node = parents[node]
    shortest_path.append("start")
    return shortest_path

# 寻找加权的最短路径
def dijkstra():
    # 查询到目前开销最小的节点
    node = find_lowest_cost_node(costs)
    # 只要有开销最小的节点就循环（这个while循环在所有节点都被处理过后结束）
    while node is not None:
        # 获取该节点当前开销
        cost = costs[node]
        # 获取该节点相邻的节点
        neighbors = graph[node]
        # 遍历当前节点的所有邻居
        for n in neighbors.keys():
            # 计算经过当前节点到达相邻结点的开销,即当前节点的开销加上当前节点到相邻节点的开销
            new_cost = cost + neighbors[n]
            # 如果经当前节点前往该邻居更近，就更新该邻居的开销
            if new_cost < costs[n]:
                costs[n] = new_cost
                #同时将该邻居的父节点设置为当前节点
                parents[n] = node
        # 将当前节点标记为处理过
        processed.append(node)
        # 找出接下来要处理的节点，并循环
        node = find_lowest_cost_node(costs)
    # 循环完毕说明所有节点都已经处理完毕
    shortest_path = find_shortest_path()
    shortest_path.reverse()
    print(shortest_path)
# 测试
dijkstra()#['start', 'b', 'a', 'end']

8. 贪婪算法

8.1 如何识别及解决NP难问题

NP难问题常有的特征：

元素较少时算法的运行速度非常快，但随着元素数量的增加，速度会变得非常慢。
涉及“所有组合”的问题通常是NP完全问题。
不能将问题分成小问题，必须考虑各种可能的情况。这可能是NP完全问题。
如果问题涉及序列（如旅行商问题中的城市序列）且难以解决，它可能就是NP完全问题。
如果问题涉及集合（如广播台集合）且难以解决，它可能就是NP完全问题。
如果问题可转换为集合覆盖问题或旅行商问题，那它肯定是NP完全问题。

贪婪算法寻找局部最优解，企图以这种方式获得全局最优解。

对于NP完全问题，还没有找到快速解决方案。
面临NP完全问题时，最佳的做法是使用近似算法。
贪婪算法易于实现、运行速度快，是不错的近似算法。

8.2 理论

贪心算法在当前看来最好的选择，虽然贪心算法不能对所有问题都得到整体最优解，但对许多问题它能产生整体最优解。如单源最短路经问题，最小生成树问题等。在一些情况下，其最终结果却是最优解的很好近似，况且节省了很多时间。
基本要素:
(1) 贪心选择性质:
是指所求问题的整体最优解可以通过一系列局部最优的选择，即贪心选择来达到。这是贪心算法可行的第一个基本要素，也是贪心算法与动态规划算法的主要区别。
动态规划是通过挑选子问题的解找出最优解。
动态规划算法通常以自底向上（具体-抽象）的方式解各子问题，而贪心算法则通常以自顶向下（抽象-具体）的方式进行，以迭代的方式作出相继的贪心选择，每作一次贪心选择就将所求问题简化为规模更小的子问题。对于一个具体问题，要确定它是否具有贪心选择性质，必须证明每一步所作的贪心选择最终导致问题的整体最优解。
(2) 最优子结构性质:
当一个问题的最优解包含其子问题的最优解时，称此问题具有最优子结构性质。问题的最优子结构性质是该问题可用动态规划算法或贪心算法求解的关键特征。

下面的图说明了两者算法的区别：贪婪是近似算法，动态规划可以得到最优解。

9. 动态规划

参考连接：动态规划专题

10. 其他有用的算法

在前面的二分查找示例中，每当用户登录Facebook时，Facebook都必须在一个庞大的数组中查找，核实其中是否包含指定的用户名（也可以用散列表,或者分布式查询）。
前面说过，在这种数组中查找时，最快的方式是二分查找，但问题是每当有新用户注册时，都必须将其用户名插入该数组并重新排序，因为二分查找仅在数组有序时才管用。如果能将用户名插入到数组的正确位置就好了，这样就无需在插入后再排序。为此，有人设计了一种名为二叉查找树（binary search tree）的数据结构。

千里足行~始于足下

关注

2
点赞
踩
0

收藏

觉得还不错? 一键收藏
0
评论
【算法图解】——算法必备

1. 大O表示法大O表示法：O(n)O{(n)}O(n),n代表操作数，指出了算法在最坏情况下的速度有多快，因为我们不仅要知道算法运行完的时间，还需要知道运行时间如何随着数据的增长而增加。比如：二分查找即折半查找，简单查找是一个一个的找，对于10个元素的有序列表，简单查找：O(10)O{(10)}O(10)=10，折半查找：O(log10)O{(log 10)}O(log10)=4，默认以2为底，那么从10000个找呢？两者的操作数10000，14，可见差别多大。为什么操作数代表了时间呢？因为计算
复制链接

扫一扫