Euler向前、向后及改进差分格式，预估校正格式matlab实现（微分方程数值解作业）

Euler向前、向后及改进差分格式

主函数

"""
主程序（Matlab）：通过调用不同的方法实现不同的差分格式

% 参数：(odefun,xspan,y0,m)=====(函数f,[x0,xN],解的初始值，区间等分)
% 欧拉向前差分格式：ode_euler(odefun,xspan,y0,m)
% 欧拉向后差分格式：ode_imeuler(odefun,xspan,y0,m)
% 改进的欧拉差分格式：euler_trape(odefun,xspan,y0,m)
"""
function mainNu
us=dsolve('Du-t*u=0','u(0)=1','t'); %解析解
us1= matlabFunction(us);%符号变量转化为函数句柄
fplot(us1,[0,1])%[x,y]=fplot(fun,lims,…) 只返回用来绘图的点，并不绘图，可以自己调用plot(x,y)来绘制图形
%,(['$$u=',latex(us),'$$'],'interpreter','latex')
odefun=@(t,u)t*u;
H=[0.1,0.05,0.02];
S={':*b',':^r',':og'};
re=zeros(1,3);
for i=1:3
    h=H(i);
    [t,y]=ode_euler(odefun,[0,1],1,1/h);%% 调用函数
    hold on 
    ss=S(i);
    plot(t,y,cell2mat(ss));
    re(i)=norm(y-us1(t),'fro');
end
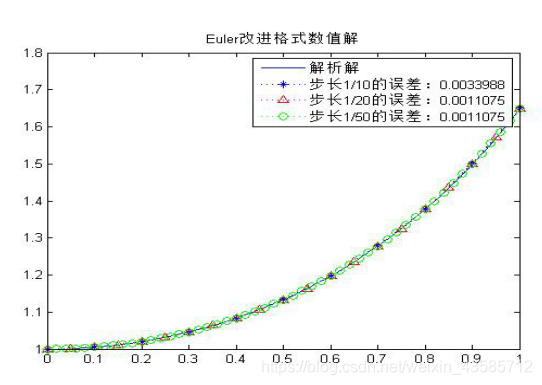
title('Euler向前格式数值解')
legend('解析解',['步长1/10的误差：',num2str(re(1))],['步长1/20的误差：',num2str(re(2))],['步长1/50的误差：',num2str(re(2))])
end

三种差分函数

"子函数"
"欧拉向前差分格式"
function varargout=ode_euler(odefun,xspan,y0,m)
if nargin<4
    m=10;
end
x=linspace(xspan(1),xspan(2),m+1);%离散节点的值
y=[y0,zeros(1,m)];
%k=1:m因为y(1)=y0,matlab的下标从1开始
for k=1:m
    h=x(k+1)-x(k);
    y(k+1)=y(k)+h*feval(odefun,x(k),y(k));
end
if nargout==0%matlab定义的nargout：返回函数输出参数的数量。
    plot(x,y)
else
    [varargout{1:2}]=deal(x(:),y(:));%varargout{1:2}，取前2个参数
end
end
"欧拉向后差分格式(实验常用的技巧多次使用预校正公式)"
function varargout=ode_imeuler(odefun,xspan,y0,m)
if nargin<4
    m=10;
end
x=linspace(xspan(1),xspan(2),m+1);
y=[y0,zeros(1,m)];
%k=1:m因为y(1)=y0,matlab的下标从1开始
for k=1:m
    h=x(k+1)-x(k);
    yp=y(k)+h*feval(odefun,x(k),y(k));
    while 1
        y(k+1)=y(k)+h*feval(odefun,x(k),y(k));
        if abs(y(k+1)-yp)<=1e-6
            break
        end
        yp=y(k+1);
    end
end
if nargout==0%matlab定义的nargout：返回函数输出参数的数量。
    plot(x,y)
else
    [varargout{1:2}]=deal(x(:),y(:));%varargout{1:2}，取前2个参数
end
end
"改进的欧拉差分格式"
function varargout=euler_trape(odefun,xspan,y0,m)
if nargin<4
    m=10;
end
x=linspace(xspan(1),xspan(2),m+1);
y=[y0,zeros(1,m)];
%k=1:m因为y(1)=y0,matlab的下标从1开始
for k=1:m
    h=x(k+1)-x(k);
    yp=y(k)+h*feval(odefun,x(k),y(k));
    while 1
        y(k+1)=y(k)+0.5*h*(feval(odefun,x(k),y(k))+feval(odefun,x(k+1),yp));
        if abs(y(k+1)-yp)<=1e-6
            break
        end
         yp=y(k+1);
    end
end
if nargout==0%matlab定义的nargout：返回函数输出参数的数量。
    plot(x,y)
else
    [varargout{1:2}]=deal(x(:),y(:));%varargout{1:2}，取前2个参数
end
end

预估校正格式

n=input('enter''n'':')%输入剖分数
for i=1:n+1
    t(i)=(i)/(n+1);
end
u(1)=1;
for i=1:1:n
    w(i+1)=u(i)+1/n*t(i)*u(i);
    u(i+1)=u(i)+1/n/2*(t(i)*u(i)+t(i)*w(i+1));
end
x=0:1/(n):1;
y=exp(0.5*x.^2);
plot(x,y,'r')
hold on
f=linspace(0,1,n+1);
plot(f,u,'o')
for i=1:1:n+1
 e(i)=abs(y(i)-u(i));
end
e1=max(e);
legend(['精确解',’预估-校正法','location','northwest')
xlabel('t')
ylabel('u')
title('预估-校正法')