[LCA]最近公共祖先（倍增+树剖）

Bamboo_Day

已于 2023-04-26 19:53:03 修改

阅读量690

点赞数 1

分类专栏：随笔 C++入门基础教程文章标签： c++ 算法图论

于 2023-04-12 21:18:46 首次发布

本文链接：https://blog.csdn.net/weixin_43617116/article/details/130116678

版权

C++入门基础教程同时被 2 个专栏收录

27 篇文章 26 订阅

订阅专栏

随笔

26 篇文章 0 订阅

订阅专栏

倍增求 LCA

概念引入

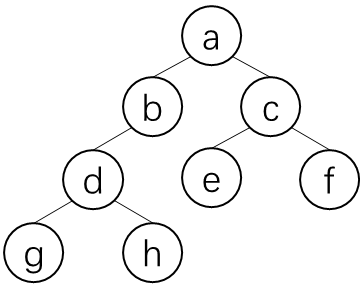
在这里插入图片描述

祖先

祖先其实很好理解，一个节点的 **父节点以及父节点的父节点以及父节点的父节点的父……**都是这个节点的祖先

比如说上面的 $d$ 节点， $b$ 节点和 $a$ 节点都是它的祖先

$k$ 级祖先

称节点 𝑥 的父节点为 𝑥 的 1 级祖先。节点 𝑥 父节点的 𝑘 级祖先称为节点 𝑥 的 𝑘 + 1 级祖先。

比如，节点 $a$ 就是节点 $d$ 的二级祖先

引例

假设节点 $i$ 的 $k$ 级祖先是 $j$ ， $j$ 的 $k 1$ 级祖先为 $x$ ，那么 $x$ 为 $i$ 的几级祖先？

显然是 $（ k + k 1 ）$ 级祖先

深度

记 $d e p (x)$ 为节点 𝑥 的深度。
若 𝑥 为根结点，则 $d e p (x) = 1$ ；
否则 $d e p (x) = d e p (f) + 1$ ，其中 $f$ 为 $x$ 的父节点。

基本思想

考虑树上深度相同的节点对 (𝑥, 𝑦)，设其 𝐿𝐶𝐴 为节点 𝐿。
$\Delta = dep(x) - dep(L)$
显然， $\Delta > 0$ ，为节点对 $(x, y)$ 与 $L$ 的深度差，即节点 $(x, y)$ 想要抵达节点 $L$ ，需要向上跳跃的距离。

我们只需要求出节点 $x$ 或 $y$ 的 $\Delta$ 级祖先，就求出了节点对 $(x, y)$ 的最近公共祖先，但 $\Delta$ 具体的值并不明确，采用尝试的办法。
不妨记 $\geq 0)$ 𝐹为节点 𝑥 的 $2^k$ 级祖先。
由倍增思想，从高位 $log_2 n)$ 向低位( $0$ )依次枚举 $i$ 。
若 $F (x, i) = F (y, i)$ ，说明 $x$ 的 $2^i$ 级祖先在节点 $L$ 到根节点的路径上，不作处理。
否则， $\leftarrow F(x,i) , y \leftarrow F(y,i)$ 。
当 $i = 0$ 枚举完毕后， $x$ , $y$ 节点的父节点即为其最近公共祖先。

代码实现

$F (x, k)$ 则可以通过递推在预处理中求出。
$F (x, 0) = f$
$F (x, k) = F (F (x, k - 1), k - 1))$
这可以通过一次树上遍历完成。
若 $\not= dep(y)$ ，不妨设 $d e p (x) > d e p (y)$ ，先通过一次倍增，将节点 $x$ 向上跳跃至与节点 $y$ 深度相同。

Code

#include <bits/stdc++.h>
#define ll long long
const int INF = 0x3f3f3f3f;
const int N = 5e5+10; 
using namespace std;
int n, m , s;
vector <int> e[N];
int fa[N][25],dep[N];
void get_father(int pos,int f){
	fa[pos][0] = f;
	dep[pos] = dep[f] + 1;
	for(int i = 1; i <= 20; i++){
		fa[pos][i] = fa[fa[pos][i-1]][i-1];
	}
	for(auto j : e[pos]){
		if(j == f) continue;
		get_father(j,pos);
	}
}
int LCA(int x, int y){
	if(dep[x] < dep[y]){
		swap(x,y);
	}
	for(int i = 20; i >= 0; i--){
		if(dep[fa[x][i]] >= dep[y]){
			x = fa[x][i];
		}
	}
	if(x == y) return x;
	for(int i = 20; i >= 0; i--){
		if(fa[x][i] != fa[y][i]){
			x = fa[x][i];
			y = fa[y][i];
		}
	}
	return fa[x][0];
}
int main(){
	cin >> n >> m >> s;
	for(int i = 1;i < n; i++){
		int u, v;
		cin >> u >> v;
		e[u].push_back(v);
		e[v].push_back(u);
	}	
	get_father(s,0);
	while(m--){
		int x, y;
		cin >> x >> y;
		cout << LCA(x,y) << endl;
	}
	return 0;
}

树链剖分求 LCA

概念引入

这里树链剖分也叫重链剖分

子树大小

以节点 $x$ 为根的子树所含节点数称为该子树的大小，记为 $S (x)$ 。

轻重儿子

记 $V (x)$ 为节点 $x$ 的子节点集合。对于 $\in V(x)$ ，满足 ∀𝑣 ∈ 𝑉 𝑥 , 𝑆 𝑣 ≤ 𝑆(𝑢)，则 $u$ 称为节点 $x$ 的重儿子，其余子节点称为 $x$ 的轻儿子。特别地，若 $\phi$ ，节点 $x$ 不存在重儿子。（一个节点可能有多个重儿子，任取其一）

重链

这里不介绍有关 $df s$ 序，因为~~用不到~~
重儿子与其父节点的连边叫做一条重链

轻链

~~当然不是重链就是轻链了~~

这里的重链和轻链都是满足可加性的

在这里插入图片描述
例如这里标小红点的是轻儿子，粗线是重链

跳链头

在重链剖分中有一种很重要的操作是跳链头

重链相当于高速公路，每次可以跳到深度最小的节点的父节点（不然的话就是一条重链上出不去了）
轻链相当于普通公路，一次只能跳一步

重链剖分

重链剖分由两次 $df s$ 完成

第一次 $df s$ ：计算每一棵子树的 $s i ze, d e pt h, Hso n, F a t h er$
第二次 $df s$ ：按照先重儿子，后其他儿子的顺序，对树上的结点进行重新编号（仅用于求 LCA 不需要），并维护每一个结点所处的重链的链头 原来的编号 $t o p (x)$ 。

Code

int top[N],hson[N],siz[N],dep[N],f[N];
void dfs1(int x, int fa){
	hson[x] = 0;
	f[x] = fa;
	siz[x] = 1;
	dep[x] = dep[fa] + 1;
	for(auto to : e[x]){
		if(to == fa) continue;
		dfs1(to,x);
		siz[x] += siz[to];
		if(siz[hson[x]] < siz[to]) hson[x] = to;
	}
	
}
void dfs2(int x, int tp){
	top[x] = tp;
	if(!hson[x]) return;
	dfs2(hson[x],tp);
	for(auto to : e[x]){
		if(to == f[x] || to == hson[x]) continue;
		dfs2(to,to);
	}
}

求 LCA

使用重链剖分求 $L C A$ ，就是不断交替跳链头的过程，直到两个结点游标处于同一条重链上。
交替：优先跳链头深度深的游标。

然后返回深度浅的节点就行

Code

int LCA(int x, int y){
	while(top[x] != top[y]){
		if(dep[top[x]] < dep[top[y]]) swap(x,y);
		x = f[top[x]];
	}
	if(dep[x] < dep[y]) return x;
	return y;
}