NFA到DFA的转化（保证能讲明白）

如何将下图的NFA转化为DFA呢？

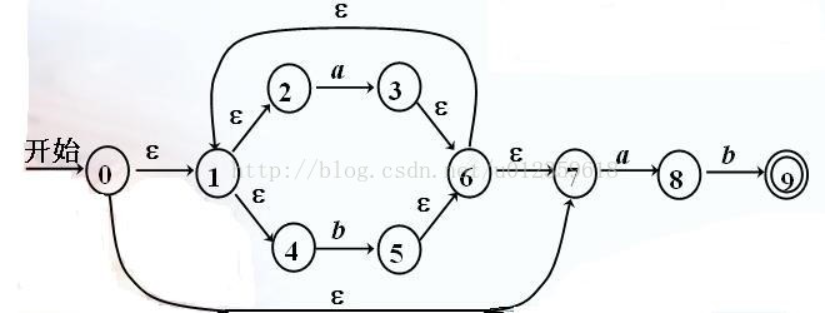
图1

解答如下:

1. 求出 $\epsilon \_closure(s)$
   $\epsilon \_closure(s)$表示由状态 $s$ 经由条件 $\epsilon$ 可以到达的所有状态的集合

ε _ c l o s u r e ( 0 ) = { 0 , 1 , 2 , 4 , 7 } ε\_closure(0)=\{0,1,2,4,7\} ε_closure(0)={0,1,2,4,7}
ε _ c l o s u r e ( 1 ) = { 1 , 2 , 4 } ε\_closure(1)=\{1,2,4\} ε_closure(1)={1,2,4}
ε _ c l o s u r e ( 2 ) = { 2 } ε\_closure(2)=\{2\} ε_closure(2)={2}
ε _ c l o s u r e ( 3 ) = { 1 , 2 , 3 , 4 , 6 , 7 } ε\_closure(3)=\{1,2,3,4,6,7\} ε_closure(3)={1,2,3,4,6,7}
ε _ c l o s u r e ( 4 ) = { 4 } ε\_closure(4)=\{4\} ε_closure(4)={4}
ε _ c l o s u r e ( 5 ) = { 1 , 2 , 4 , 5 , 6 , 7 } ε\_closure(5)=\{1,2,4,5,6,7\} ε_closure(5)={1,2,4,5,6,7}
ε _ c l o s u r e ( 6 ) = { 1 , 2 , 4 , 6 , 7 } ε\_closure(6)=\{1,2,4,6,7\} ε_closure(6)={1,2,4,6,7}
ε _ c l o s u r e ( 7 ) = { 7 } ε\_closure(7)=\{7\} ε_closure(7)={7}
ε _ c l o s u r e ( 8 ) = { 8 } ε\_closure(8)=\{8\} ε_closure(8)={8}
ε _ c l o s u r e ( 9 ) = { 9 } ε\_closure(9)=\{9\} ε_closure(9)={9}

2. 下面的A,B,C…表示一种状态。如A表示 { 0 , 1 , 2 , 4 , 7 } \{0,1,2,4,7\} {0,1,2,4,7},其实就是$\epsilon \_closure(0)$

为了读懂下面的内容，在这里先解释几个东西。

• $\epsilon \_closure(move(A,a))$ 中的 $move(A,a)$是什么意思呢？
  它代表从状态A，经过a到达的状态。
  A状态是 ε _ c l o s u r e ( 0 ) = { 0 , 1 , 2 , 4 , 7 } ε\_closure(0) = \{0,1,2,4,7\} ε_closure(0)={0,1,2,4,7}，在 { 0 , 1 , 2 , 4 , 7 } \{0,1,2,4,7\} {0,1,2,4,7}里面，对每一个元素都考虑其是否通过a到达了某个状态，观察图1，只有状态2和7经过了a，分别到达了3和8，所以 $move(A,a)$ = { 3 , 8 } \{3,8\} {3,8}，从而有 ε _ c l o s u r e ( m o v e ( A , a ) ) = ε _ c l o s u r e ( { 3 , 8 } ) = { 1 , 2 , 3 , 4 , 6 , 7 , 8 } ε\_closure(move(A,a)) = ε\_closure(\{3,8\}) = \{1,2,3,4,6,7,8\} ε_closure(move(A,a))=ε_closure({3,8})={1,2,3,4,6,7,8}， { 1 , 2 , 3 , 4 , 6 , 7 , 8 } \{1,2,3,4,6,7,8\} {1,2,3,4,6,7,8}是未出现过的状态，所以可把它取名为B状态(其它名字也行).
• ε _ c l o s u r e ( { 3 , 8 } ) = { 1 , 2 , 3 , 4 , 6 , 7 , 8 } ε\_closure(\{3,8\}) = \{1,2,3,4,6,7,8\} ε_closure({3,8})={1,2,3,4,6,7,8}是怎么来的呢？
  因为在步骤1我们已经知道， ε _ c l o s u r e ( 3 ) = { 1 , 2 , 3 , 4 , 6 , 7 } ε\_closure(3)=\{1,2,3,4,6,7\} ε_closure(3)={1,2,3,4,6,7}， ε _ c l o s u r e ( 8 ) = { 8 } ε\_closure(8)=\{8\} ε_closure(8)={8} ，然后取它们的并集就得到了 { 1 , 2 , 3 , 4 , 6 , 7 , 8 } \{1,2,3,4,6,7,8\} {1,2,3,4,6,7,8}.
  
  这样应该解释明白了。继续往下看，然后不懂的话再倒回来看看。

ε _ c l o s u r e ( 0 ) = { 0 , 1 , 2 , 4 , 7 } = A ε\_closure(0) = \{0,1,2,4,7\} = A ε_closure(0)={0,1,2,4,7}=A
ε _ c l o s u r e ( m o v e ( A , a ) ) = ε _ c l o s u r e ( { 3 , 8 } ) = { 1 , 2 , 3 , 4 , 6 , 7 , 8 } = B ε\_closure(move(A,a)) = ε\_closure(\{3,8\}) = \{1,2,3,4,6,7,8\} = B ε_closure(move(A,a))=ε_closure({3,8})={1,2,3,4,6,7,8}=B
ε _ c l o s u r e ( m o v e ( A , b ) ) = ε _ c l o s u r e ( 5 ) = { 1 , 2 , 4 , 5 , 6 , 7 } = C ε\_closure(move(A,b)) = ε\_closure(5) = \{1,2,4,5,6,7\} = C ε_closure(move(A,b))=ε_closure(5)={1,2,4,5,6,7}=C
ε _ c l o s u r e ( m o v e ( B , a ) ) = ε _ c l o s u r e ( { 3 , 8 } ) = { 1 , 2 , 3 , 4 , 6 , 7 , 8 } = B ε\_closure(move(B,a)) = ε\_closure(\{3,8\}) = \{1,2,3,4,6,7,8\} = B ε_closure(move(B,a))=ε_closure({3,8})={1,2,3,4,6,7,8}=B
ε _ c l o s u r e ( m o v e ( B , b ) ) = ε _ c l o s u r e ( { 5 , 9 } ) = { 1 , 2 , 4 , 5 , 6 , 7 , 9 } = D ε\_closure(move(B,b)) = ε\_closure(\{5,9\}) =\{1,2,4,5,6,7,9\} = D ε_closure(move(B,b))=ε_closure({5,9})={1,2,4,5,6,7,9}=D
ε _ c l o s u r e ( m o v e ( C , a ) ) = ε _ c l o s u r e ( { 3 , 8 } ) = { 1 , 2 , 3 , 4 , 6 , 7 , 8 } = B ε\_closure(move(C,a)) = ε\_closure(\{3,8\}) = \{1,2,3,4,6,7,8\} = B ε_closure(move(C,a))=ε_closure({3,8})={1,2,3,4,6,7,8}=B
ε _ c l o s u r e ( m o v e ( C , b ) ) = ε _ c l o s u r e ( 5 ) = { 1 , 2 , 4 , 5 , 6 , 7 } = C ε\_closure(move(C,b)) = ε\_closure(5) = \{1,2,4,5,6,7\} = C ε_closure(move(C,b))=ε_closure(5)={1,2,4,5,6,7}=C
ε _ c l o s u r e ( m o v e ( D , a ) ) = ε _ c l o s u r e ( { 3 , 8 } ) = { 1 , 2 , 3 , 4 , 6 , 7 , 8 } = B ε\_closure(move(D,a)) = ε\_closure(\{3,8\}) = \{1,2,3,4,6,7,8\} = B ε_closure(move(D,a))=ε_closure({3,8})={1,2,3,4,6,7,8}=B
ε _ c l o s u r e ( m o v e ( D , b ) ) = ε _ c l o s u r e ( 5 ) = { 1 , 2 , 4 , 5 , 6 , 7 } = C ε\_closure(move(D,b)) = ε\_closure(5) = \{1,2,4,5,6,7\} = C ε_closure(move(D,b))=ε_closure(5)={1,2,4,5,6,7}=C

3. 画出DFA状态转换表
   步骤2中有A,B,C,D四种情况，其中A是初始情况（ ε _ c l o s u r e ( 0 ) = { 0 , 1 , 2 , 4 , 7 } ε\_closure(0)=\{0,1,2,4,7\} ε_closure(0)={0,1,2,4,7}. 多说几句，在NFA图1中，是从0出发的，所以初始情况是$\epsilon \_closure(0)$，那假设如果是从X开始，则初始情况是$\epsilon \_closure(X)$）

看步骤2， ε _ c l o s u r e ( m o v e ( A , a ) ) = ε _ c l o s u r e ( { 3 , 8 } ) = { 1 , 2 , 3 , 4 , 6 , 7 , 8 } = B ε\_closure(move(A,a)) = ε\_closure(\{3,8\}) = \{1,2,3,4,6,7,8\} = B ε_closure(move(A,a))=ε_closure({3,8})={1,2,3,4,6,7,8}=B，所以A行a列填B，其他同理。

	a	b
A	B	C
B	B	D
C	B	C
D	B	C

4. 根据DFA状态转换表画出DFA状态转换图

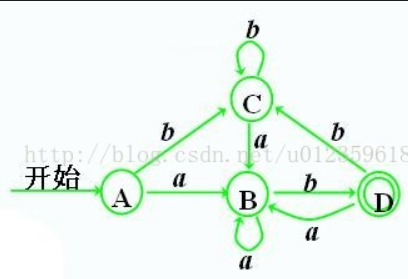
看步骤3的表格，A经过a到B，A经过b到C，B经过a到B，以此类推…

参考：
NFA到DFA的转化🔗