Towards Principled Methods For Training Generative Adversarial Networks
文章目录
全文梳理
从整体的角度来简单梳理一下整篇论文:
首先在介绍中解释了训练生成模型的传统方法选择KL散度为目标函数,由于其不对称的性质,当两个分布的密度不一样的时候,选取不同的分布作为参考可能会获得不同的结果。而生成对抗网络的本质是最小化 J S D JSD JSD散度, J S D JSD JSD散度本身是不对称的, G A N s GANs GANs在理论上的训练可以分为两步:第一步是将辨别器训练为最优辨别器,此时关于 θ \theta θ代价函数可以近似 J S D JSD JSD散度,然后再训练生成器,在 θ \theta θ上做梯度更新。但是实际上这种方案是不可行的,在辨别器最优的时候,训练生成器时梯度的更新会消失。于是人们又选择了另外一种代价函数作为替代,虽然解决了生成器梯度消失的问题,但是生成器的梯度更新不稳定,收敛也很慢。
然后在第二部分中,作者分别证明了 P r P_r Pr和 P g P_g Pg实际都是处于一个高维空间中的低维流形上。证明了两个非全维度的流形实际上分本无法完美对齐。然后得出了两个低维流形之间总存在一个完美的辨别器,可以将这两个流形完美的分开。然后证明了刚才所说的完美辨别器其实在两个流形是恒定存在的,并非我们通过反向传播学习得到的,实际上我们并未通过反向传播学习到任何东西。
然后给出了定理:两个非全维度非完美对齐的流形彼此位于任意接近的位置,这些散度也将是最大化的。生成器的样本也许看起来很好,但是 K L KL KL散度仍是无穷。因此,定理2.3指出了一个事实:尝试使用散度来测试分布间的相似性是一个不好的想法。如果这些散度总是最大的,那么尝试通过梯度下降去最小化他们是不可能的。
接着分析了原始的代价函数中存在的问题:当辨别器接近于完美辨别器时(误差为0),那么训练生成器的梯度会变为0,也就是所谓的梯度消失。然后又分析了用以解决梯度消失的代价函数在训练时所存在的问题:生成器梯度的期望时一个具有无穷梯度和方差的柯西分布,这会造成梯度越来越大,训练不稳定。
第三部分中,作者认为要解决上述问题首先要破坏他们的假设条件:向辨别器的输入添加连续的噪声。用来平滑概率的分布。并从中找到了灵感,通过一步一步的改进,最终选择了一种指标: w a s s e r s t e i n wasserstein wasserstein距离。
摘要
本文的目标是朝着完全理解生成对抗网络的训练动态过程迈进理论性的一步。
本片论文主要分为三个部分:
- 第一个部分介绍当前的问题。
- 第二个部分致力于研究和严格证明包括训练不稳定和饱和等训练GANs时出现的问题。
- 第三个部分探讨解决这些问题的实际和理论方向,并介绍了研究它们的新工具。
1. 介绍
G A N s GANs GANs取得了巨大的成功,并运用在多个领域,但是很难训练。近期的文章总是致力于探索稳定的结构,尽管略有小成,这样的方式对于结构的调整非常敏感,使得很难用新的变体进行实验,也很难将这些变体用于新的领域,严重限制了GANs的应用。对于其训练的不稳定性几乎没有理论上的解释,本文出现的目的就是为了打破此现状。
G A N s GANs GANs生成器的结构与其他方法(如变分自动编码器)的结构差别不大。毕竟其核心就是先从简单的先验分布z~p(z)采样,然后输出最终的样本 g θ ( z ) g_\theta(z) gθ(z),有时在终端添加噪声。而 g θ ( z ) g_\theta(z) gθ(z)总是以 θ \theta θ为参数的神经网络,主要的差别在于g θ _\theta θ是如何训练的。
训练生成模型的传统方法
传统的训练生成模型的方式依赖于最大化概率,或者等价的最小化位置数据分布 P r P_r Pr和生成器分布 P g P_g Pg(取决于 θ \theta θ)之间的KL散度,假定两个分布都以密度 P r P_r Pr和 P g P_g Pg连续,这些方法尝试最小化:
K L ( P r ∣ ∣ P g ) = ∫ χ P r ( x ) log P r ( x ) P g ( x ) d x KL(P_r||P_g)=\int_\chi P_r(x) \log\frac{P_r(x)}{P_g(x)}dx KL(Pr∣∣Pg)=∫χPr(x)logPg(x)Pr(x)dx
此cost Function有一个好的性质:它在 P g = P r P_g=P_r Pg=Pr处有一个唯一的最小值,也不需要未知的 P r ( x ) P_r(x) Pr(x)的知识来优化。但是 P r P_r Pr和 P g P_g Pg之间的这种散度是非对称的:
- 如果 P r ( x ) > P g ( x ) P_r(x)>P_g(x) Pr(x)>Pg(x),说明x很容易被当成是一个真实样本,这就是通常所说的 m o d e d r o p p i n g mode\space dropping mode dropping现象的核心原因:很大区域的 P r P_r Pr值很高,而 P g P_g Pg的值很小或者为0时。注意当 P r ( x ) > 0 但 P g ( x ) → 0 P_r(x)>0但P_g(x)\rightarrow0 Pr(x)>0但Pg(x)→0时 K L KL KL内部的积分很快增长至无穷,意味着代价函数因为生成器分布未包含部分数据花费极高的代价。(mode dropping :生成分布的某个集中部分和真实分布逼近,其他部分未能和真实分布逼近,因而造成很大的代价)
- 如果 P r ( x ) < P g ( x ) P_r(x)\lt P_g(x) Pr(x)<Pg(x),说明x很容易被当成一个真实样本,这种情况下生成器输出的图像看起来不真实。在这种情况下, P r ( x ) → 0 但 P g ( x ) > 0 P_r(x)\rightarrow0但P_g(x)>0 Pr(x)→0但Pg(x)>0,我们可以看到 K L KL KL内的值趋于0,意味着代价函数会在生成看起来不真实的图像上花费极低的代价。
如果我们最小化 K L ( P g ∣ ∣ P r ) KL(P_g||P_r) KL(Pg∣∣Pr),情况就会相反,这意味着新的代价函数会花费很高的代价生成看起来不合理的图像。
生成对抗网络训练生成模型的方法
生成对抗网络时最小化 J S JS JS散度,这种散度是上述两个代价函数的对称中间点:
J S D ( P r ∣ ∣ P g ) = = 1 2 K L ( P r ∣ ∣ P A ) + 1 2 K L ( P g ∣ ∣ ( P A ) JSD(P_r||P_g)==\frac{1}{2}KL(P_r||P_A)+\frac{1}{2}KL(P_g||(P_A) JSD(Pr∣∣Pg)==21KL(Pr∣∣PA)+21KL(Pg∣∣(PA)
P A P_A PA是平均分布,密度为 P r + P g 2 \frac{P_r+P_g}{2} 2Pr+Pg。
人们猜想GANs在生成看起来真实的图像的成功是因为转而选择了新的代价函数。但是问题还远远没有结束。
生成对抗网络的形成有两步:
-
训练辨别器 D D D来最大化 L ( D , g θ ) = E x ~ P g [ l o g ( 1 − D ( x ) ) ] L(D,g_\theta)=E_{x~P_g}[log(1-D(x))] L(D,gθ)=Ex~Pg[log(1−D(x))] (1)
易得,最优的辨别的形式为: D ∗ ( x ) = p r ( x ) P r ( x ) + P g ( x ) D^*(x)=\frac{p_r(x)}{P_r(x)+P_g(x)} D∗(x)=Pr(x)+Pg(x)pr(x), (2)
并且在辨别器最优的条件下有 L ( D , g θ ) = 2 J S D ( P r ∣ ∣ P g ) − 2 log 2 L(D,g_\theta)=2JSD(P_r||P_g)-2\log2 L(D,gθ)=2JSD(Pr∣∣Pg)−2log2(证明略)
-
此时,将式(1)作为 θ \theta θ的函数来最小化,等于最小化 J S JS JS散度(训练生成器,最小化JS散度,拉近两个分布的距离)
理论上,人们希望可以将辨别器尽可能训练到接近最优(这样代价函数才能近似看成 J S D JSD JSD),然后做关于 θ \theta θ的梯度下降,交替这两个步骤。
实际上,这样是不可行的。当辨别器训练的越来越好,对于生成器的更新会越来越糟。
GAN原论文认为这是由于饱和引起的,并换成了另外一种相似的不具有此问题的代价函数。但是,即使是新的代价函数,生成器的更新也会变糟,优化过程极其不稳定。因此,出现了几个问题:
- 为什么辨别器越好,生成器的更新越糟?不管是原来的代价函数还是新的代价函数
- 为什么GAN的训练如此不稳定?
- 新的代价函数和服从一个和JSD相似的散度吗?如果是的话,其性质又是什么?
- 有什么方法能避免这些问题吗?
本文的基础贡献就是解答这些问题,更重要的是介绍正确分析这些问题的工具。作者提供了新的方向来避免GANs的不稳定问题,深度分析了不稳定问题背后的理论。最终,作者提出了一系列开放性的问题和疑问,这些问题决定了研究的新方向。
2. 不稳定的来源
作者首先阐述了为什么训练器能够轻易训练到收敛。
理论告诉我们训练的生成器代价最多为 2 log 2 − 2 J S D ( P r ∣ ∣ P g ) 2\log2-2JSD(P_r||P_g) 2log2−2JSD(Pr∣∣Pg),但是,实际上如果能将 D D D训练到收敛,让其误差变为 0 0 0,他们之间的 J S D JSD JSD最大化, 如图 1 如图1 如图1,这种情况能够发生的唯一方式就是分布不连续或者他们有不相交的支撑集。
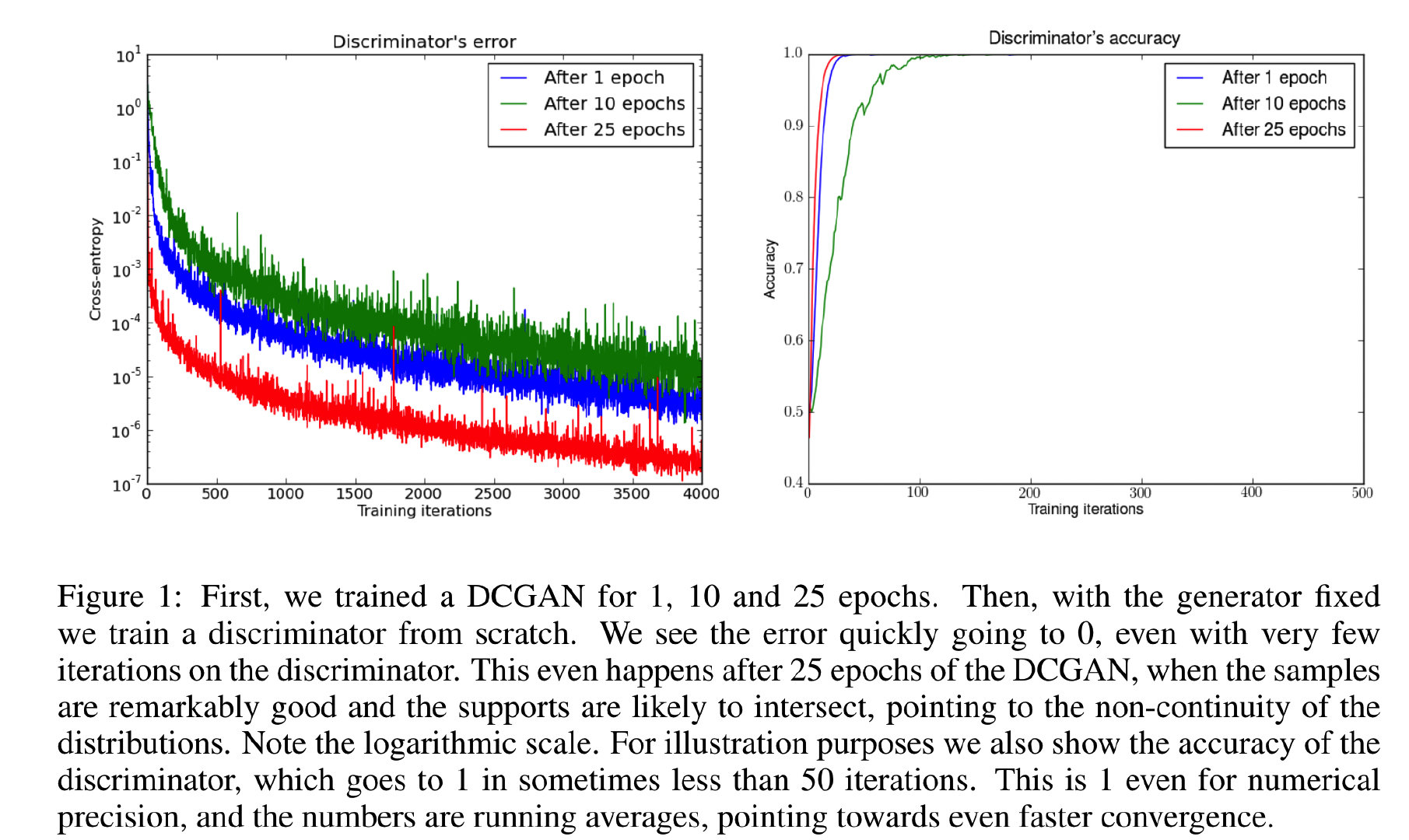
分布不连续的一个可能的原因是他们的支撑集位于低维度流形上。
1)有充分的经验性和理论性证据相信 P r P_r Pr确实集中于一个低维度流形上。
对于 G A N s GANs GANs来说, P g P_g Pg是通过从先验分布 z ~ p ( z ) z~p(z) z~p(z)中采样,然后施加函数 g : Z → χ g:Z\rightarrow\chi g:Z→χ得到的,所以 P g P_g Pg的支撑集包含于 g ( Z ) g(Z) g(Z)。 如果 Z 的维度低于 χ 的维度 如果Z的维度低于\chi的维度 如果Z的维度低于χ的维度(通常如此),那么 P g P_g Pg不可能是连续的。这是因为在大多数情况下 g ( Z ) g(Z) g(Z)包含在一个低维度流形的并集中, 因此 g ( Z ) 在 χ 上测度为 0 因此g(Z)在\chi上测度为0 因此g(Z)在χ上测度为0(低维度流形在高纬度流形上测度为0,如一维的点在二维空间中测度为0)。虽然直观,但是不可小觑的是,有n维参数并不完全意味着图像位于n维流形上。
论点1: g : Z → χ g:Z\rightarrow\chi g:Z→χ是一个由仿射变换和点态非线性变换组成的函数( R e L U , l e a k y R e L U ReLU,leaky\space ReLU ReLU,leaky ReLU或者严格递增的函数( s i g m o i d sigmoid sigmoid , t a n h tanh tanh, s o f t p l u s softplus softplus等)),那么 g ( Z ) g(Z) g(Z)包含在一个维度最高为Z的维度的流形的并集中。因此如果 Z Z Z的维度小于 χ \chi χ的维度,那么 g ( Z ) g(Z) g(Z)在 χ \chi χ上的测度为 0 0 0。
个人理解:如果将低维度的数据经过仿射和点态非线性变换映射到高纬度上,那么变换后的数据其实并未真正的升高维度,而是映射到了多个不高于原来维度的流形的并集上,此时这些映射后的数据在高维空间内的测度为0。
举个例子,如果将一条二维空间上的直线映射到三维空间中的直线,但其实并没有改变这条直线是二维的本质,其依然处于一个二维的流形上。我们在三位空间上对这条直线的测度依然为 0 0 0。
放在GAN中来说,因为我们的噪声是从低维的先验分布z~p(z)中采样而来的数据,通过生成器映射为假高维数据 P g P_g Pg,但它其实只是映射在高维空间中几个低维流形的并集上,并未真正处于高维流形上。
2) P g P_g Pg只是低维数据通过生成器 g g g映射的假高维数据,其实际依然位于低维度流形上。
综上所述,如果 P r P_r Pr和 P g P_g Pg的支撑集不相交或者位于低维度流形上,那么**在他们之间总有一个完美的辨别器,这才导致了辨别器轻易就能训练到误差为0。**作者下面详细的解释了为什么这会导致生成器不可靠的训练过程。
2.1 完美辨别器定理
作者首先介绍了 P r P_r Pr和 P g P_g Pg有不相交支撑集的情况。
如果一个辨别器在包含 P r P_r Pr的支撑集上取值为1,在包含 P g P_g Pg的支撑集上取值为0,那么我们称其准确率为1。即 P r [ D ( x ) = 1 ] = 1 P_r[D(x)=1]=1 Pr[D(x)=1]=1以及 P g [ D ( x ) = 0 ] = 1 P_g[D(x)=0]=1 Pg[D(x)=0]=1.
定理2.1:如果两个分布 P r P_r Pr和 P g P_g Pg分别有两个互不相交的支撑子集 M M M和 P P P,那么有一个光滑最优的辨别器 D ∗ : χ → [ 0 , 1 ] D^*:\chi\rightarrow[0,1] D∗:χ→[0,1],对于所有 x ∈ M ∪ P x\in M\cup P x∈M∪P,此辨别器精确率为1, ▽ x D ∗ ( x ) = 0 \triangledown _x D^\ast(x)=0 ▽xD∗(x)=0
在下一个定理中,作者将去掉不相交的假设,将上述定理推广到两个流形的情况。如果两个流形在大部分空间都完美匹配,那么就没有辨别器能将他们分开。直觉上来讲,两个低维度流形在大部分空间完美匹配的机率非常之小:对于两个曲线在空间空特定部分的匹配,他们无法以任何任意小的方式被扰动且依旧满足此性质(大幅度匹配),上面所说都是从直觉上来讲,作者下面从概念上定义了两个完美对齐的流形,并且证明了在任何任意小的扰动下这种情况都无法以概率1成立。
定义2.1: M M M和 P P P是 F F F的两个无界子流形, x ∈ M ∪ P x\in M\cup P x∈M∪P是两个子流形的交点。 T x M T_xM TxM代表 M M M在 x x x附近的切面空间如果 T x M + T x P = T x F T_xM+T_xP=T_xF TxM+TxP=TxF我们称 M M M和 P P P横截相交于 x x x.
**定义2.2:**如果有一处 x ∈ M ∪ P x\in M\cup P x∈M∪P,使得 M M M和 P P P不横截相交于 x x x,我们称这两个有界流形完美对齐。
有趣的是我们可以安全的假设在实际中任何两个流形永远不会完美对齐。能够这样说是因为一个任意小的随机扰动将会让这两个随机流形横截相交,或者根本不相交。
论点2: M M M和 P P P是两个 d d d维空间的的非全维度子流形(n<d), η , η ′ \eta,\eta' η,η′是任意独立连续的连续的随机变量(噪声),因此可以定义被扰动的流形为: M ~ = M + η \tilde M=M+\eta M~=M+η 以及 P ~ = P + η ′ \tilde P = P+\eta' P~=P+η′,有
P η , η ′ ( M ~ 与 P ~ 未完美对齐 ) = 1 P_{\eta,\eta'}(\tilde M与\tilde P未完美对齐)=1 Pη,η′(M~与P~未完美对齐)=1
定义2.1 + 定义2.2+论点2都是为了推出没有两个流形能够完美对齐。
论点3: M M M和 P P P是 d d d维空间内两个非完美对齐非全维的流形, L = M ∩ P L=M\cap P L=M∩P,如果 M M M和 P P P无界, L L L也是一个流形,并且维度低于 M M M和 P P P中任意一个;如果 M M M和 P P P有界, L L L是一个严格低于 4 4 4维的流形的集合。这两种情况下, L L L不管是在 M M M还是 P P P上的测度都为 0 0 0。
现在我们将陈述对于两个流形情况下的完美辨别器的结果。
定理2.2: P r P_r Pr和 P g P_g Pg是两个分布,他们的支撑集在两个接近的流形 M M M和 P P P上 , M M M和 P P P非完美对齐且非全维度,我们进一步假定 P r P_r Pr和 P g P_g Pg在各自的流形上是连续的,意味着如果有一个集合 A A A在 M M M上测度为 0 0 0,那么 P r ( A ) = 0 P_r(A)=0 Pr(A)=0( P g P_g Pg同理)。那么则存在一个最优的辨别器 D ∗ : χ → [ 0 , 1 ] D^\ast:\chi\rightarrow[0,1] D∗:χ→[0,1],此辨别器对 M M M或者 P P P上的任意 x x x准确率为1, D ∗ D^\ast D∗在x的邻域内光滑,并有 ▽ x D ∗ ( x ) = 1 \triangledown_xD^\ast(x)=1 ▽xD∗(x)=1
定理2.1和定理2.2告诉我们光滑和恒定的辨别器在 M M M和 P P P中处处都有,两个流形中的辨别器是恒定的这个事实指出了我们并没有真的通过反向传播学到任何东西。
作者表述了下面的关于 P r P_r Pr和 P g P_g Pg的定理
定理2.3: P r P_r Pr和 P g P_g Pg是两个支撑集位于流形M和P上的分布,流形M和P非全维非完美对其。我们假定 P r P_r Pr和 P g P_g Pg在各自的流形上连续,则:
J S D ( P r ∣ ∣ P g ) = log 2 JSD(P_r||P_g)=\log2 JSD(Pr∣∣Pg)=log2
K L ( P r ∣ ∣ P g ) = + ∞ KL(P_r||P_g)=+\infin KL(Pr∣∣Pg)=+∞
K L ( P g ∣ ∣ P r ) = + ∞ KL(P_g||P_r)=+\infin KL(Pg∣∣Pr)=+∞
注意到即使两个流形彼此位于任意接近的位置,这些散度也达到最大化。生成器的样本也许看起来很好,但是 K L KL KL散度仍是无穷。因此,定理2.3指出了一个事实:尝试使用散度来测试分布间的相似性是一个不好的想法。如果这些散度总是最大的,那么尝试通过梯度下降去最小化他们是不可能的。
我们想要选取一个更软一点的指标,该指标包含流形中点的距离。第三章将会解释另外一种度量方式。
2.2 每个代价函数的后果和问题
定理2.1和定理2.2展示了一个重要的事实:如果两个分布有不相交的支撑集或者是位于低维度的流形上,那么最优的辨别器是完美的,并且其梯度几乎处处为0。
2.2.1 原始的代价函数
现在我们将探索当我们通过辨别器向生成器传递梯度时会发生什么。
和目前所做的经典分析的一个重要的差别是我们将探索一个最优辨别器的近似的理论,而不是使用未知的真实的辨别器。我们将这种当这种近似越来越好,我们或者会看到消失的梯度或者会看到实际中那种不稳定的表现,这取决于我们所用的代价函数。
定理2.4(生成器梯度消失): g θ : Z → χ g_\theta:Z\rightarrow\chi gθ:Z→χ是一个可微函数,服从分布 P g P_g Pg, P r P_r Pr是真实数据分布,D是可微的辨别器,如果定理2.1和定理2.2满足, ∣ ∣ D − D ∗ ∣ ∣ < ϵ ||D-D^\ast||\lt\epsilon ∣∣D−D∗∣∣<ϵ,且 E z ~ p ( z ) [ ∣ ∣ J θ g θ ( z ) ∣ ∣ 2 2 ≤ M 2 ] E_{z~p(z)}[||J_\theta g_\theta(z)||^2_2\le M^2] Ez~p(z)[∣∣Jθgθ(z)∣∣22≤M2],有
∣ ∣ ▽ θ E z ~ p ( z ) [ log ( 1 − D ( g θ ( z ) 2 < M ϵ 1 − ϵ ] ||\triangledown _\theta E_{z~p(z)}[\log (1-D(g_\theta(z)_2\lt M\frac{\epsilon}{1-\epsilon}] ∣∣▽θEz~p(z)[log(1−D(gθ(z)2<M1−ϵϵ]
**推论2.1:**在与定理2.4相同的假设下:
lim ∣ ∣ D − D ∗ ∣ ∣ → 0 ▽ θ [ log ( 1 − D ( g θ ( z ) ) ) ] = 0 \lim_{||D-D^\ast||\rightarrow 0}\triangledown_\theta[\log(1-D(g_\theta(z)))]=0 lim∣∣D−D∗∣∣→0▽θ[log(1−D(gθ(z)))]=0
这说明了当辨别器越来越逼近最优辨别器的时候,生成器的梯度消失了。为了完整性,这一点被实验性的在图2中被证实。这种情况发生时很糟糕的,因为生成器的代价函数接近于 J S JS JS散度是取决于辨别器近似最优辨别器的程度的。这向我们指明了一个基础性问题:或者是辨别器不够准确,或者生成器的梯度消失。
这样的话用此代价函数就很难进行训练了,如果非要用此代价函数训练,那么就得用户自己控制辨别器的训练量,这样的话GAN的训练就极其难了。
简而言之就是作者证明了一个事实:如果把辨别器训练的特别好,那么生成器的梯度就会消失。如果想要继续使用此代价函数,那么就需要用户自己权衡辨别器的训练程度,这让GAN的训练过程非常艰难。
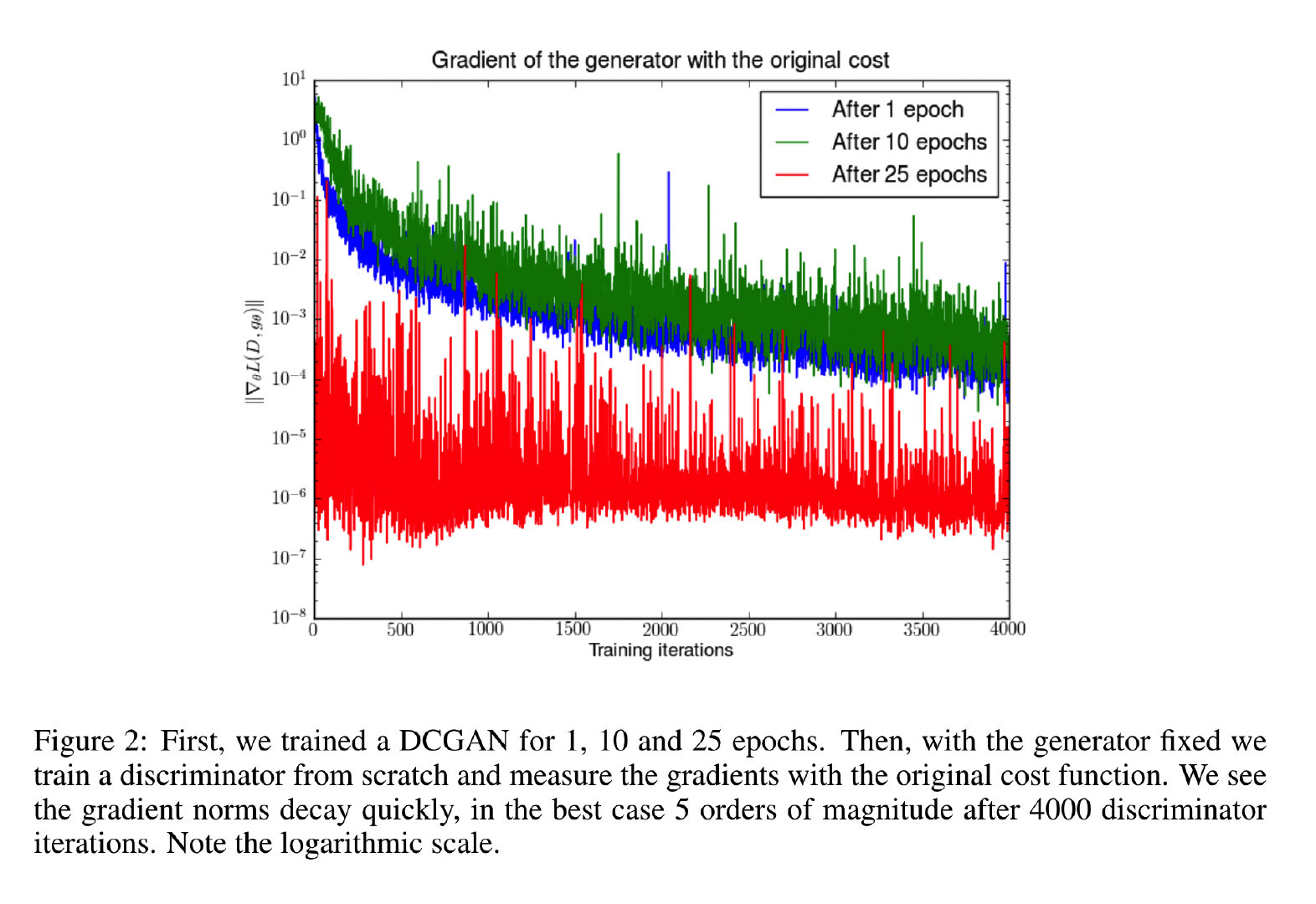
2.2.2 用 − log D -\log D −logD替代
为了避免当辨别器准确率太高时生成器梯度消失的问题,人们为生成器选择了另外一种梯度:
$\triangle\theta=\triangledown_\theta E_{z~p(z)}[-\log D(g_\theta(z))] $
作者先证明了这个梯度正在优化哪一个代价函数,然后作者证明了虽然这个地图不再忍受梯度消失的问题,但是在对最优辨别器进行噪声近似的情况下,它却造成了更新不稳定。
**定理2.5:**P_r和 P g P_g Pg是两个连续分布,密度分别是 P r P_r Pr和 P g P_g Pg。 D ∗ = P r P r + P g D^\ast=\frac{P_r}{P_r+P_g} D∗=Pr+PgPr是最优辨别器,以值 θ 0 \theta_0 θ0固定,有
E z ~ p ( z ) [ − ▽ θ log D ∗ ( g θ ( z ) ) ∣ θ = θ 0 ] = ▽ θ [ K L ( P g θ ∣ ∣ P r ) − 2 J S D ( P g θ ∣ ∣ P r ) ] ∣ θ = θ 0 E_{z~p(z)}[-\triangledown_\theta\log D^\ast(g_\theta(z))|_{\theta=\theta_0}]=\triangledown_\theta[KL(P_{g_\theta}||P_r)-2JSD(P_{g_\theta}||P_r)]|_{\theta=\theta_0} Ez~p(z)[−▽θlogD∗(gθ(z))∣θ=θ0]=▽θ[KL(Pgθ∣∣Pr)−2JSD(Pgθ∣∣Pr)]∣θ=θ0 (3)
观察式(3),这是反着的 K L KL KL减去2倍的 J S D JSD JSD。
首先,JSD与KL符号相反,意味着他们将两个分布推远。第二,式中的KL是 K L ( P g ∣ ∣ P r ) KL(P_g||P_r) KL(Pg∣∣Pr),在前面曾经提到过,这种KL将花费很大的代价生成看起来不真实的图像,划分极低的代价在“mode dropping”,JSD是对称的所以没有这种现象。这就解释了我们在实际中所看到的,GANS(稳定时)能够产生看起来很好的样本,并且证实了猜想:GAN遭受了大量的mode dropping。
然后作者转向了 关于噪声版本的真实辨别器不稳定性的结果。
定理2.6(生成器梯度更新的不稳定性): g θ : Z → χ g_\theta:Z\rightarrow\chi gθ:Z→χ是一个服从分布 P g P_g Pg的可微函数, P r P_r Pr是真实数据的分布,如果定理2.1或者定理2.2中的一个的条件满足,D是辨别器, D ∗ − D = ϵ D^\ast-D=\epsilon D∗−D=ϵ是一个被x索引但独立于每个x的集中的高斯过程,并且 ▽ x D ∗ − ▽ x D = r \triangledown_xD^\ast-\triangledown_xD=r ▽xD∗−▽xD=r是另外一个被x索引但独立于每个x的集中的高斯过程。那么:
E z ~ p ( z ) [ − ▽ θ log D ( g θ ( z ) ) ] E_{z~p(z)}[-\triangledown_\theta\log D(g_\theta(z))] Ez~p(z)[−▽θlogD(gθ(z))]的坐标是一个集中的具有无穷期望和方差的柯西分布。
即使我们忽略这种更新有无穷方差的事实,我们也无法忽略这种更新的分布是集中的这个事实,意味着如果我们对更新划定界限,那么期望的更新将会是0,对梯度不提供任何反馈。
由于D的噪声和 ▽ D 是不相关的 \triangledown D是不相关的 ▽D是不相关的”这个假设太强,我们在图3中展示了在训练一个稳定的DCGAN的任何阶段,除了它已经收敛,当我们将辨别器训练到接近最优时梯度的范数时如何剧烈增长的。
在所有的情况下,使用这种梗系你都会导致样本质量的下降。曲线中的噪声也显示了梯度的方差正在增加,这就是人们所知的在优化中的收敛缓慢和不稳定的表现。
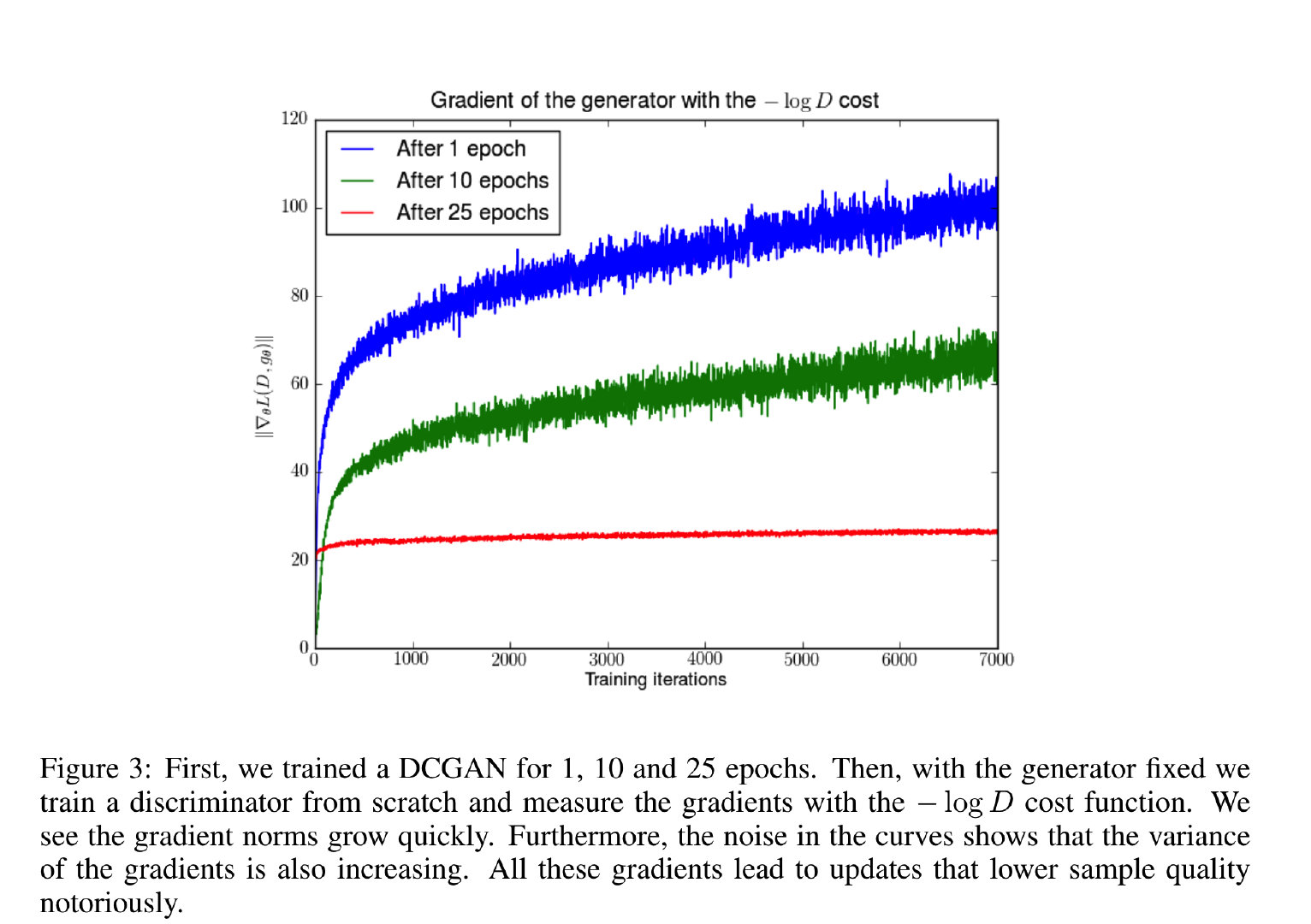
整个第二部分先分析了原始的代价函数,证明了如果用原始的代价函数训练,如果将辨别器训练的太好,生成器的梯度会消失;如果不想生成器的梯度消失,那么就要权衡辨别器的训练程度,这样对于用户来说难度太高了。
然后分析了另一种代价函数-logD,这种代价函数解决了生成器梯度消失的问题,但是作者证明了此代价函数梯度的期望是一个集中的具有无穷方差的柯西分布,这导致生成器梯度更新时特别不稳定,收敛特别慢。
3. 迈向软一些的指标和分布
一个很重要的问题就是如何去修复不稳定性和消失的梯度问题。我们能做的就是打破这些理论的假设:向辨别器的输入添加连续的噪声。用来平滑概率的分布。
**定理3.1:**如果X有分布 P x P_x Px,支撑集在M上, ϵ \epsilon ϵ为密度为 P ϵ P_\epsilon Pϵ的完全连续变量,那么 P X + ϵ P_{X+\epsilon} PX+ϵ完全连续且密度为
P X + ϵ ( x ) = E y ~ p X [ P ϵ ( x − y ) ] P_{X+\epsilon}(x)=E_{y~p_X}[P_\epsilon(x-y)] PX+ϵ(x)=Ey~pX[Pϵ(x−y)]
= ∫ M P ϵ ( x − y ) d P X ( y ) =\int_MP_\epsilon(x-y)dP_X(y) =∫MPϵ(x−y)dPX(y)
推论3.1:
这个定理告诉我们密度 P X + ϵ ( x ) P_{X+\epsilon}(x) PX+ϵ(x)与 P X P_X PX的支撑集中的点的平均距离成反比,以这些点的概率为权重。
在 P X P_X PX的支撑集是一个流形的情况下,我们将会有到这些沿着流形的点的距离的加权平均。我们如何选择噪声的分布 ϵ \epsilon ϵ会影响我们所选择的距离的概念。例如在作者的推论中,我们可以看到通过该表指数项内的范数来改变协方差矩阵所造成的影响。因此带有不同衰减类型的不同噪声可用。
现在, P g + ϵ 和 P r + ϵ P_{g+\epsilon}和P_{r+\epsilon} Pg+ϵ和Pr+ϵ之间的最优辨别器为:
D ∗ ( x ) = P r + ϵ P r + ϵ + P g + ϵ D^\ast(x)=\frac{P_{r+\epsilon}}{P_{r+\epsilon}+P_{g+\epsilon}} D∗(x)=Pr+ϵ+Pg+ϵPr+ϵ
作者想要计算传入生成器的梯度是什么
**定理3.2:**P_r和P_g是两个分别在M和P上有 支撑集的分布, ϵ ~ N ( 0 , σ 2 I ) \epsilon~N(0,\sigma^2I) ϵ~N(0,σ2I),则传入生成器的梯度形式为:
这个定理证明了我们将样本 g θ ( z ) g_\theta(z) gθ(z)赶向沿着数据流形的那些点,被这些点的概率以及从样本到这些点的距离所加权。第二项让样本点原理高概率的样本,这和对比散度的思想类似:降低样本的自由能量,增加数据点的自由能量。但是这还存在一些问题。
推论3.2:
与定理3.2的主要不同在于作者将所有的噪声样本朝着数据流形移动。这会保护辨别器将对抗样本测度为0.
有趣的现象是,如果两个支撑集在非常接近的流形上的分布 P r P_r Pr和 P g P_g Pg , 这些噪声项会使噪声分布 P r + ϵ P_{r+\epsilon} Pr+ϵ和 P g + ϵ P_{g+\epsilon} Pg+ϵ几乎重叠,他们之间的 J S D JSD JSD非常的小,与无噪声的 P r P_r Pr和 P g P_g Pg形成强烈的反差,无噪声情况下他们的 J S D JSD JSD不管两个流形的距离多接近都是最大化的。
作者认为用噪声变体的 J S D JSD JSD来度量两个原始分布之间的相似性,但这取决于噪声的数量,并且也不是 P r P_r Pr和 P g P_g Pg天然的度量。幸运的是,还有别的选择。
**定义3.1:**对于两个在 χ \chi χ上的分布 P P P和 Q Q Q,他们的 W a s s e r s t e i n Wasserstein Wasserstein度量 W ( P , Q ) W(P,Q) W(P,Q):
W ( P , Q ) = inf γ ∈ Γ ∫ χ × χ ∣ ∣ x − y ∣ ∣ 2 d γ ( x , y ) W(P,Q)=\inf_{\gamma\in\Gamma}\int_{\chi\times\chi}||x-y||_2d\gamma(x,y) W(P,Q)=infγ∈Γ∫χ×χ∣∣x−y∣∣2dγ(x,y)
其中 Γ \Gamma Γ是在 χ × χ \chi\times\chi χ×χ上所有具有边缘P和Q的可能的交点的集合。
W a s s e r s t e i n Wasserstein Wasserstein距离也有其他名字:交通度量和挖土机距离。挖土机距离非常有解释意义:P从其支撑集到Q的支撑集上为了匹配Q的概率块而运输概率的最低花费。
直觉上,当我们减少噪声时, P X P_X PX和 P X + ϵ P_{X+\epsilon} PX+ϵ越来越相似,很容易再次看到 J S D ( P X ∣ ∣ P X + ϵ ) JSD(P_X||P_{X+\epsilon}) JSD(PX∣∣PX+ϵ)再次最大化,不论噪数量多少。下面的推论说明了 W a s s e r s t e i n Wasserstein Wasserstein度量不会出现这种情况,当我们将降低噪声的方差时, J S D ( P X ∣ ∣ P X + ϵ ) JSD(P_X||P_{X+\epsilon}) JSD(PX∣∣PX+ϵ)变为0
**推论4:**如果 ϵ \epsilon ϵ是一个均值为0的随机向量,我们有:
W ( P X , P X + ϵ ) ≤ V 1 2 W(P_X,P_{X+\epsilon})\le V^{\frac{1}{2}} W(PX,PX+ϵ)≤V21
其中, V = E [ ∣ ∣ ϵ ∣ ∣ 2 2 ] V=E[||\epsilon||^{2}_{2}] V=E[∣∣ϵ∣∣22] 是 ϵ \epsilon ϵ的方差
现在我们要研究一下没有任何噪音的分布 P r P_r Pr和 P g P_g Pg之间的距离,即使他们的支撑集位于不同的流形上,因为流形越接近,那么生成样本点离数据流形上的实际点也就越接近。
更进一步,我们希望能有一种方式来评价生成模型,不管他们是否连续。这是一个完全还未被解决的问题。下一个定理将没有任何噪声的 P r P_r Pr和 P g P_g Pg的 W a s s e r s t e i n Wasserstein Wasserstein距离与 P r + ϵ P_{r+\epsilon} Pr+ϵ与 p g + ϵ p_{g+\epsilon} pg+ϵ的散度联系起来,因为 P r + ϵ P_{r+\epsilon} Pr+ϵ与 p g + ϵ p_{g+\epsilon} pg+ϵ是连续分布,这种散度是一种合理的评估,能够尝试去最小化,因为一个训练在这些分布上的辨别器将会近似他们之间的 J S D JSD JSD,提供光滑的梯度。
定理3.3
定理3.3为我们指出了一个有趣的想法,式(6)中的两项能够被控制。
第一项能通过对噪声退火来降低,当辨别器在噪声输入上训练时第二项能够通过一个GAN来最小化,因为该辨别器能够逼近两个连续分布之间的 J S D JSD JSD。
这样做的一个最大的好处是我们不用再为训练计划二担心。由于这些噪声,我们可以将辨别器训练至最优而不不会出现任何问题,且可以得到光滑可解释的梯度。同时,最小化 P r P_r Pr与 P g P_g Pg这两个我们所关心的没有噪声的分布之间的距离,









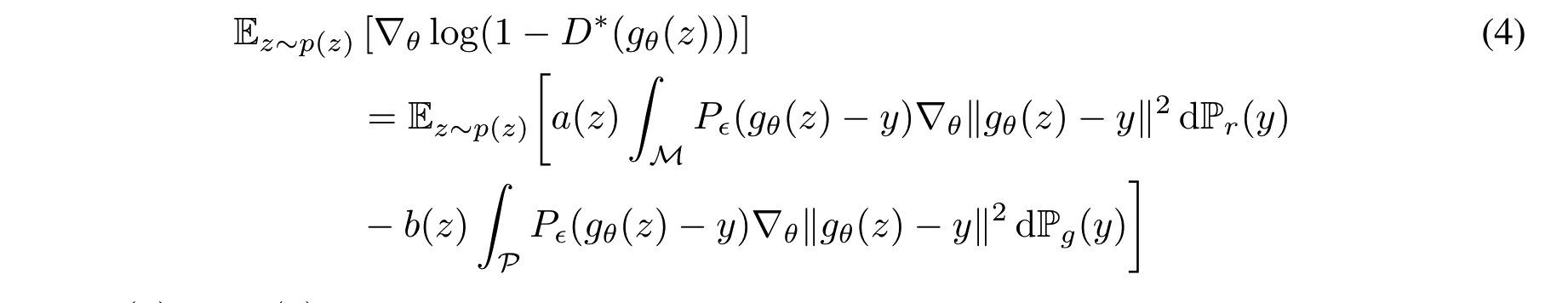
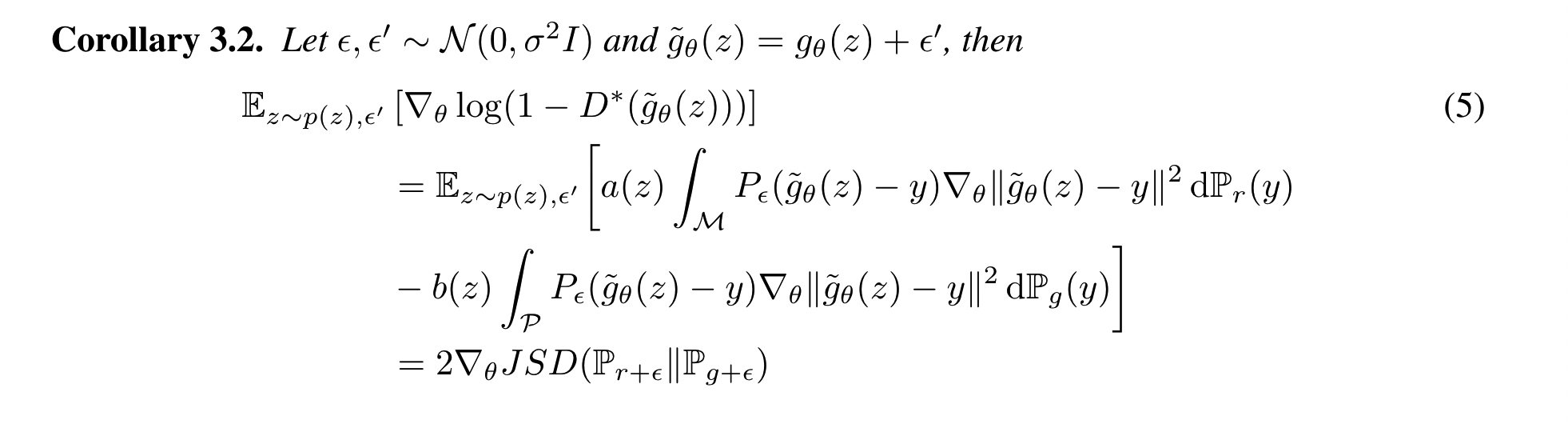















 3万+
3万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








