奇异值分解(SVD)原理与在降维中的应用

参考资料

奇异值分解(Singular Value Decomposition，以下简称SVD)是在机器学习领域广泛应用的算法，它不光可以用于降维算法中的特征分解，还可以用于推荐系统，以及自然语言处理等领域。是很多机器学习算法的基石。本文就对SVD的原理做一个总结，并讨论在在PCA降维算法中是如何运用运用SVD的。

1. 回顾特征值和特征向量

我们首先回顾下特征值和特征向量的定义如下:
$$Ax=\lambda x$$
其中A是一个 $n\times n$ 的实对称矩阵， $x$ 是一个 $n$ 维向量，则我们说 $\lambda$ 是矩阵A的一个特征值，而 $x$ 是矩阵A的特征值 $\lambda$ 所对应的特佂向量。

求出特佂值和特征向量有什么好处呢?

就是我们可以将矩阵A特征分解。如果我们求出了矩阵A的 $n$ 个特征值 ${\lambda }_1\le {\lambda }_2\le \dots \le {\lambda }_n$, 以及这 $n$ 个特征值所 对应的特征向量 { w 1 , w 2 , … w n } \left\{w_{1}, w_{2}, \ldots w_{n}\right\} {w1​,w2​,…wn​} ，，如果这 $n$ 个特征向量线性无关，那么矩阵A就可以用下式的特征分解表示:浅紫色文字
$$A=W\Sigma W^{-1}$$
其中W是这 $n$ 个特佂向量所张成的 $n\times n$ 维矩阵，而 $\Sigma$ 为这 $n$ 个特佂值为主对角线的 $n\times n$ 维矩阵。

一般我们会把W的这 $n$ 个特佂向量标准化，即满足 ${\Vert w_i\Vert }_2=1$ ，或者说 $w_i^T{w}_i=1$ ，此时 $W$ 的 $n$ 个特征向量为标准正交基，满足 $W^{T}W=I$ ，即 $W^T=W^{-1}$ ， 也就是说 W为酉矩阵(方阵)。

这样我们的特征分解表达式可以写成
$$A=W\Sigma W^T$$

注意到要进行特佂分解，矩阵A必须为方阵。那/如果A不是方阵，即行和列不相同时，我们还可以对矩阵进行分解吗? 答案是可以，此时我们的SVD登场了。

2. SVD的定义

SVD也是对矩阵进行分解，但是和特征分解不同，SVD并不要求要分解的矩阵为方阵。假设我们的矩阵A是一个m $\times n$ 的矩阵，那么我们定义矩阵A的SVD为:
$$A=U\Sigma V^T$$
其中 U是一个 $m\times m$ 的矩阵， $\Sigma$ 是一个 $m\times n$ 的矩阵，除了主对角线上的元素以外全为 0 , 主对角线上的每个元素都称为奇异值， $\mathrm{V}$ 是一个 $n\times n$ 的矩阵。U和V都是酉矩阵，即满足 $U^{T}U=I,V^{T}V=I$ 。下图可以很形象的看出上面SVD的定义:

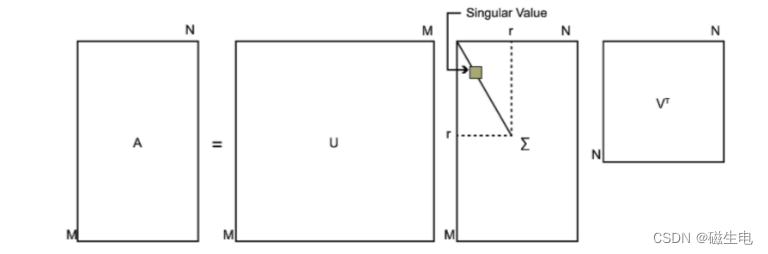
那么我如何求出SVD分解后的 $U,\Sigma ,V$ 这三个矩阵呢?

如果找们将A的转置和A做矩阵乘法，那么会得到 $n\times n$ 的一个方阵 $A^{T}A$ 。既然 $A^{T}A$ 是方阵，那么我们就可以进行特佂分解，得到的特佂值和特征向量满足下式:

$$\left(A^{T}A\right)v_i={\lambda }_i{v}_i$$
这样找们就可以得到矩阵 $A^{T}A$ 的 $\mathrm{n}$ 个特征值 $\lambda$和对应的 $\mathrm{n}$ 个特征向量 $v$ 。

将 $A^{T}A$ 的所有特征向量张成一个 $n\times n$ 的矩阵 $V$ ,就 是 我 们 SVD 公 式 里 面 的$V$ 矩阵了。一般我们将 $\mathrm{V}$ 中的每个特征向量叫做A的右奇异向量。

如果找们将A和A的转置做矩阵乘法，那么会得到 $m\times m$ 的一个方阵 $A{A}^T$ 。既然 $A{A}^T$ 是方阵，那么我们就可以进行特佂分解，得到的特佂值和特征向量满足下式:
$$\left(A{A}^T\right)u_i={\lambda }_i{u}_i$$
这样找们就可以得到矩阵 $A{A}^T$ 的 $\mathrm{m}$ 个特征值和对应的 $\mathrm{m}$ 个特佂向量 $u$ 了。将 $A{A}^T$ 的所有特征向量张成一个 $m\times m$ 的矩阵 $\mathrm{U}$ ，就是我们SVD公式里面的 U矩阵了。一般我们将U中的每个特征向量叫做A的左奇异向量。

$U$和 $V$我们都求出来了 ，现在就剩下奇异矩阵$\Sigma$没有求出来了。由于$\Sigma$除了对角线上是奇异值其他位置都是0，那我们只需要求出每个奇异值σ就可以了。

我们注竟到:
$$A=U\Sigma V^T\Rightarrow AV=U\Sigma V^{T}V\Rightarrow AV=U\Sigma \Rightarrow A{v}_i={\sigma }_i{u}_i\Rightarrow {\sigma }_i=A{v}_i/u_i$$
这样我们可以求出我们的每个奇异值，进而求出奇异值矩阵 $\Sigma$ 。

上面还有一个问题没有讲，就是我们说 $A^{T}A$ 的特征向量组成的就是我们SVD中的 $\mathrm{V}$ 矩阵，而 $A{A}^T$ 的特征向量组成的就是我们SVD中的$U$矩阵，这有什么 根据吗? 这个其实很容易证明，我们以V矩阵的证明为例。
$$A=U\Sigma V^T\Rightarrow A^T=V{\Sigma }^T{U}^T\Rightarrow A^{T}A=V{\Sigma }^T{U}^{T}U\Sigma V^T=V{\Sigma }^2{V}^T$$
上式证明使用了: $U^{T}U=I,{\Sigma }^T\Sigma ={\Sigma }^2$ 。可以看出 $A^{T}A$ 的特征向量组成的的确就是我们SVD中的V知阵。类似的方法可以得到 $A{A}^T$ 的特征向量组成 的就是我们SVD中的U矩阵。

进一步我们还可以看出我们的特征值矩阵等于奇异值矩阵的平方，也就是说特征值和奇异值满足如下关系：
$${\sigma }_i=\sqrt{{\lambda }_i}$$
这样也就是说，我们可以不用 ${\sigma }_i=A{v}_i/u_i$ 来计算奇异值，也可以通过求出 $A^{T}A$ 的特征值取平方根来求奇异值。

3. SVD计算举例

这里我们用一个简单的例子来说明矩阵是如何进行奇异值分解的。我们的矩阵A定义为：
$$\mathbf{A}=\left(\begin{array}{ll}0& 1\\ 1& 1\\ 1& 0\end{array}\right)$$
我们首先求出 $A^{T}A$ 和 $A{A}^T$
$$\begin{array}{rl}{\mathbf{A}}^{\mathbf{T}}\mathbf{A}& =\left(\begin{array}{lll}0& 1& 1\\ 1& 1& 0\end{array}\right)\left(\begin{array}{ll}0& 1\\ 1& 1\\ 1& 0\end{array}\right)=\left(\begin{array}{ll}2& 1\\ 1& 2\end{array}\right)\\ \mathbf{A}{\mathbf{A}}^{\mathbf{T}}& =\left(\begin{array}{ll}0& 1\\ 1& 1\\ 1& 0\end{array}\right)\left(\begin{array}{lll}0& 1& 1\\ 1& 1& 0\end{array}\right)=\left(\begin{array}{lll}1& 1& 0\\ 1& 2& 1\\ 0& 1& 1\end{array}\right)\end{array}$$
进而求出 $A^{T}A$ 的特征值和特征向量:
$${\lambda }_1=3;v_1=\left(\begin{array}{c}1/\sqrt{2}\\ 1/\sqrt{2}\end{array}\right);{\lambda }_2=1;v_2=\left(\begin{array}{c}-1/\sqrt{2}\\ 1/\sqrt{2}\end{array}\right)$$
接着求 $A{A}^T$ 的特征值和特征向量:
$${\lambda }_1=3;u_1=\left(\begin{array}{c}1/\sqrt{6}\\ 2/\sqrt{6}\\ 1/\sqrt{6}\end{array}\right);{\lambda }_2=1;u_2=\left(\begin{array}{c}1/\sqrt{2}\\ 0\\ -1/\sqrt{2}\end{array}\right);{\lambda }_3=0;u_3=\left(\begin{array}{c}1/\sqrt{3}\\ -1/\sqrt{3}\\ 1/\sqrt{3}\end{array}\right)$$

利用 $A{v}_i={\sigma }_i{u}_i,i=1,2$ 求奇异值:
$$\begin{array}{rl}& \left(\begin{array}{ll}0& 1\\ 1& 1\\ 1& 0\end{array}\right)\left(\begin{array}{l}1/\sqrt{2}\\ 1/\sqrt{2}\end{array}\right)={\sigma }_1\left(\begin{array}{c}1/\sqrt{6}\\ 2/\sqrt{6}\\ 1/\sqrt{6}\end{array}\right)\Rightarrow {\sigma }_1=\sqrt{3}\\ & \left(\begin{array}{ll}0& 1\\ 1& 1\\ 1& 0\end{array}\right)\left(\begin{array}{c}-1/\sqrt{2}\\ 1/\sqrt{2}\end{array}\right)={\sigma }_2\left(\begin{array}{c}1/\sqrt{2}\\ 0\\ -1/\sqrt{2}\end{array}\right)\Rightarrow {\sigma }_2=1\end{array}$$
最终得到 $\mathrm{A}$ 的奇异值分解为:
$$A=U\Sigma V^T=\left(\begin{array}{ccc}1/\sqrt{6}& 1/\sqrt{2}& 1/\sqrt{3}\\ 2/\sqrt{6}& 0& -1/\sqrt{3}\\ 1/\sqrt{6}& -1/\sqrt{2}& 1/\sqrt{3}\end{array}\right)\left(\begin{array}{cc}\sqrt{3}& 0\\ 0& 1\\ 0& 0\end{array}\right)\left(\begin{array}{cc}1/\sqrt{2}& 1/\sqrt{2}\\ -1/\sqrt{2}& 1/\sqrt{2}\end{array}\right)$$

4. SVD的一些性质

上面几节我们对SVD的定义和计算做了详细的描述，似乎看不出我们费这么大的力气做SVD有什么好处。那么SVD有什么重要的性质值得我们注意呢？

对于奇异值,它跟我们特征分解中的特征值类似，在奇异值矩阵中也是按照从大到小排列，而且奇异值的下降特别的快，在很多情况下，前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上的比例。也就是说，我们也可以用最大前的k个的奇异值和对应的左右奇异向量来近似描述矩阵。也就是说：
$$A_{m\times n}=U_{m\times m}{\Sigma }_{m\times n}{V}_{n\times n}^T\approx U_{m\times k}{\Sigma }_{k\times k}{V}_{k\times n}^T$$
其中k要比n小很多，也就是一个大的矩阵A可以用三个小的矩阵$U_{m\times k,}{\Sigma }_{k\times k},V_{k\times n}^T$来表示。如下图所示，现在我们的矩阵A只需要灰色的部分的三个小矩阵就可以近似描述了。

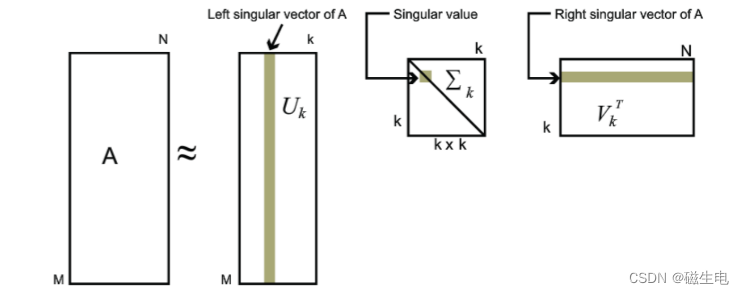
由于这个重要的性质，SVD可以用于PCA降维，来做数据压缩和去噪。也可以用于推荐算法，将用户和喜好对应的矩阵做特征分解，进而得到隐含的用户需求来做推荐。同时也可以用于NLP中的算法，比如潜在语义索引（LSI）。下面我们就对SVD用于PCA降维做一个介绍。

5. SVD用于PCA

在主成分分析 (PCA) 原理总结中，我们讲到要用PCA降维，需要找到样本协方差矩阵 $X^{T}X$ 的最大的 $\mathrm{d}$ 个特征向量，然后用这最大的 $\mathrm{d}$ 个特征向量张成 的矩阵来做低维投影降维。可以看出，在这个过程中需要先求出协方差矩阵 $X^{T}X$ ，当样本数多样本特征数也多的时候，这个计算量是很大的。

注意到我们的SVD也可以得到协方差矩阵$X^{T}X$最大的d个特征向量张成的矩阵，但是SVD有个好处，有一些SVD的实现算法可以不求先求出协方差矩阵$X^{T}X$，也能求出我们的右奇异矩阵$V$。也就是说，我们的PCA算法可以不用做特征分解，而是做SVD来完成。这个方法在样本量很大的时候很有效。实际上，scikit-learn的PCA算法的背后真正的实现就是用的SVD，而不是我们我们认为的暴力特征分解。

另一方面，注意到PCA仅仅使用了我们SVD的右奇异矩阵，没有使用左奇异矩阵，那么左奇异矩阵有什么用呢？

假设我们的样本是 $m\times n$ 的矩阵X，如果我们通过SVD找到了矩阵 $X{X}^T$ 最大的 $\mathrm{d}$ 个特征向量张成的 $m\times d$ 维矩阵U，则我们如果进行如下处理:
$$X_{d\times n}^{\prime }=U_{d\times m}^T{X}_{m\times n}$$

可以得到一个$d\times n$的矩阵X‘,这个矩阵和我们原来的$m\times n$维样本矩阵X相比，行数从m减到了d，可见对行数进行了压缩。也就是说，左奇异矩阵可以用于行数的压缩。相对的，右奇异矩阵可以用于列数即特征维度的压缩，也就是我们的PCA降维。

6. SVD小结

SVD作为一个很基本的算法，在很多机器学习算法中都有它的身影，特别是在现在的大数据时代，由于SVD可以实现并行化，因此更是大展身手。SVD的原理不难，只要有基本的线性代数知识就可以理解，实现也很简单因此值得仔细的研究。当然，SVD的缺点是分解出的矩阵解释性往往不强，有点黑盒子的味道，不过这不影响它的使用。