切西瓜(空间划分问题)

1、题目描述

题目描述： 小Py要吃西瓜，想知道切了n刀后，最多能切出多少块？请你们帮助下小Py. 给你一个正整数n（0 < n <10^3),你输出一个数字，代表最多能切多少块。 如n=1, 输出2。
示例：
输入：n = 1
输出：2

2、题目分析

这道题…如果没有理解清楚题意,那完全就是一道阴间题,只能靠瞎猜…但如果理解了话,那还是有点搞头的…

让我们捋一下大体的思路:想知道切n刀下去能最多得到多少个西瓜？我们知道,刀可以近似看作一个二维平面体,而西瓜可以看作三维空间内的一个空间体。因此,一刀下去,就相当于用一个二维平面去分割三维空间…n刀下去,就相当于用n个平面去分割三维空间…故问题就转换为了:n个平面最多可将三维空间分为多少块。

空间划分问题…对于空间立体感不是很好的朋友来说…貌似并不是一个很友好的问题,但凡事我们皆可以从小做起,我们一步步来,一步步地分析,或许也能得到一些启发。

3、问题推理

（1）直线划分问题

首先我们考虑第一个问题:用n个点最多可以将一条直线划分成多少个部分？

我们用$A(n)$来表示结果。从上图中,我们可以很容易得到:n个点,可以将其划分成$A(n)=n+1$个部分。

（2）平面划分问题

接下来我们考虑第二个问题:用n条直线最多可以将一个平面划分成多少个部分？

我们用$B(n)$来表示结果。由于这个问题不再像第一个问题这么显然了,故我们选择逐步对该问题进行分析。

首先考虑n = 1的情形:

很显然,如上图所示:$B(1)=2$。

再考虑一下n = 2的情形:

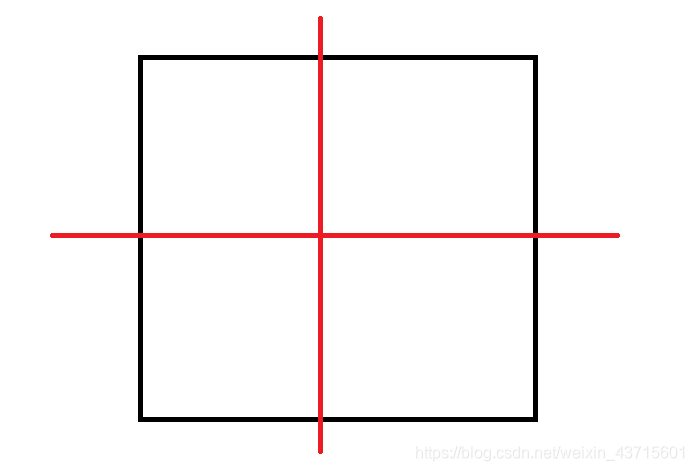
很显然,如上图所示:$B(2)=4$。

再考虑一下n = 3的情形:

这里我们需要注意一下,由于我们的目标是得到尽可能多的划分区域,故如上图所示,我这里画的第三条直线没有选择过前两条直线的交点的直线(否者得到的划分区域仅为6个),从而得到的是最大的划分区域$B(3)=7$。

从n = 3这个情形中,我们可以洞察出一个规律:即要通过n条直线划分平面而得到尽可能多的平面划分区域,我们应该使得每次引入的第i条直线(i = 1,2,…n)与前i-1条直线相交于i-1个点。

并且通过刚才对直线划分问题的研究,我们可以得知:i-1个点可以将一条直线划分成i个部分。

恰巧这i个部分,便可以使得划分的平面区域个数增加i个。

知道了这个规律后,我们便可以计算n的一般情形:

$B(n)=1+(1+2+3+...+n)$

            $=1+\frac{n\ast (n+1)}{2}$

（3）空间划分问题

最后,终于进入正题了。

如果理解了前面两个问题的话,这个问题其实并不难。

就像前面所介绍的最大平面划分问题方法一番,我们要引入的第n个平面,必将与前n-1个平面相交得到n-1直线…由于这n-1条直线在这第n个平面上,又可将这第n个平面最大划分成$B(n-1)$个区域,而这$B(n-1)$个区域,即为新增的空间划分块数。

觉得上面的解释有点抽象?那我们看如下这个例子:

如上图所示,想象XOY面为引入的第三个平面…在引入XOY面之前,整个空间被YOZ面、ZOX面划分为4个部分…而在进入了XOY面后,由于XOY面和YOZ面、ZOX面有两条交线,这两条交线将XOY面划分成了B(2)=4个部分,而这4个部分,正好使得整个空间的划分多了4个部分。

也就是说,如果我们用$C(n)$表示n个平面可将三维空间划分的最大块数,则$C(n)=C(n-1)+B(n-1)$

那么到现在我们便仅剩下最后的一个问题,就是去求解$C(n)$具体的仅关于n的表达式,如下所示:

$C(1)=1$

$C(2)=C(1)+B(1)$

$C(3)=C(2)+B(2)=C(1)+B(1)+B(2)$

$C(4)=C(3)+B(3)=C(1)+B(1)+B(2)+B(3)$

$....$

$C(n)=C(n-1)+B(n-1)$

$=C(1)+B(1)+B(2)+...+B(n-1)$

$=2+(1+\frac{1+1}{2})+(1+\frac{4+2}{2})+...+(1+\frac{(n-1{)}^2+(n-1)}{2})$

$=2+(n-1)+\frac{1}{2}\ast \frac{n\ast (n-1)}{2}+\frac{1}{2}\ast \frac{n\ast (n-1)\ast (2n-1)}{6}$

$=n+1+\frac{n^2-n}{4}+\frac{2n^3-3n^2+n}{12}$

$=\frac{n^3+5n+6}{6}$

(其中用到了平方和求和公式,如果有疑惑请点击附录:平方和求和公式)

4、算法源码

有了数学推理的BUFF加成后…这题的代码一行就足矣

print((n**3+5*n+6)//6)

附录:平方和求和公式
$$S(n)=\sum _{i=1}^n{i}^2$$
            $(n+1{)}^3-n^3=3n^2+3n+1$

            $n^3-(n-1{)}^3=3(n-1{)}^2+3(n-1)+1$

            $......$

            $3^3-2^3=3\ast 2^2+3\ast 2+1$

            $2^3-1^3=3\ast 1^2+3\ast 1+1$

            $以上各式相加得$

            $(n+1{)}^3-1^3=3S(n)+3\ast \frac{n(n+1)}{2}+n$

            $=>n^3+3n^2+3n=3S(n)+\frac{3}{2}{n}^2+\frac{5}{2}n$

            $=>S(n)=\frac{n^3}{3}+\frac{1}{2}{n}^2+\frac{1}{6}n$

            $=>S(n)=\frac{n(n+1)(2n+1)}{6}$