C++ 算法篇广度（宽度）优先搜索（BFS）

流年llyz

已于 2023-10-30 13:57:58 修改

阅读量1w

点赞数 11

分类专栏： C++算法之动态规划篇文章标签：算法 c++ 宽度优先

于 2019-01-28 10:11:09 首次发布

本文链接：https://blog.csdn.net/weixin_43736974/article/details/86672787

版权

本文深入探讨了广度优先搜索(BFS)的概念、原理及其在解决多种搜索问题中的应用，包括寻找目标节点、求解最优路径等。通过具体实例，如瓷砖、填涂颜色、求细胞数量等，展示了BFS在不同场景下的实现方法。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

广度优先遍历

广度优先遍历(Breadth_First_Search)，又称为广度优先搜索，简称BFS。

图的BFS类似于树的层序遍历。

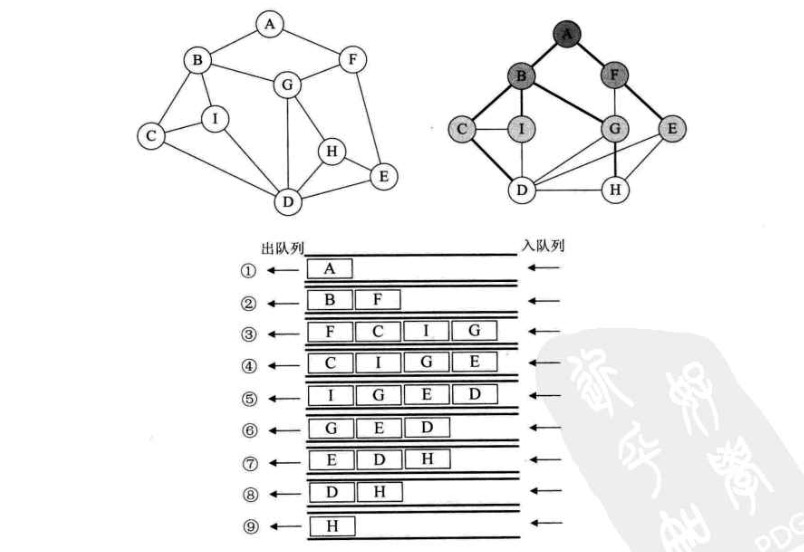
广度优先遍历

如图将左边的图变形，得到右边的图，然后一层一层的遍历。
这里借助一个队列来实现一层一层的遍历。

搜索问题一般有两种情况：一种是给出初始结点，要求寻找符合约束条件的目标结点；另一种是给出初始结点和目标结点，要求找到从初始结点到目标结点的一条路径。对于解的要求也不尽相同，有的问题要求出一个可行解，有的则要求出最优解，还有的问题要找出全部解，有时还要按照一定的顺序输出。

搜索问题中的数据结构一般要求表达要合理，有助于计算机的处理；信息要完整，能反应出状态的本质和状态之间的关系；还要节省存储空间，尽可能地提高搜索的速度。比如分油问题本来用一个三元组（x10,x7,x3）即可，但是为了输出方便，我们增加一个d,用来表示该结点的父结点（由谁拓展而来），即变成一个四元组（x10,x7,x3,d）。另外，还会用到队列来实现控制策略。当然，不能忘记状态变化过程中的重复性检查，比如哈希表，因为大多数情况下，出现重复状态是毫无意义的，会造成死循环和空间的浪费。

4. 宽度优先搜索的基本思想

宽度优先搜索（Breadth First Search，BFS），简称宽搜，又称广度优先搜索。它是从初始结点开始，应用产生式规则和控制策略生成第一层结点，同时检查目标结点是否在这些生成的结点中。若没有，再用产生式规则将所有第一层结点逐一拓展，得到第二层结点，并逐一检查第二层结点是否包含目标结点。若没有，再用产生式规则拓展第二层结点。如此依次拓展，检查下去，直至发现目标结点为止。如果拓展完所有结点，都没有发现目标结点，则问题无解。

对于以上“无向图”，从顶点 V0 开始进行宽度优先搜索，得到的一个序列为 V0，V1，V2，V3，V4，V6，V5。

宽度优先搜索是一种“盲目”搜索，所有结点的拓展都遵循“先进先出”的原则，所以采用“队列”来存储这些状态。

宽度优先搜索的算法框架如下：

void BFS
{    while (front <= rear)  // 当队列非空时做，front 和 rear 分别表示队列的头指针和尾指针  
     {     if (找到目标状态)
              做相应处理(如退出循环输出解、输出当前解、比较解的优劣);
           else
           {   拓展头结点 ;
               if( 拓展出的新结点没出现过 )
               {   rear++;
                   将新结点插到队尾 ;
               }
           }
           front++;// 取下一个结点
      }
}

如果只要求任意一个解，也可以写成以下的结构：
void BFS2
{    p = true;
     while (p)
     {    if( 头结点是目标状态 ) p = false;
          else
          {   拓展头结点 ;
              if( 拓展出的新结点没出现过 )
              {    rear++;
                   将新结点插到队尾 ;
              }
              front++;
              if(front > rear)p = false;
           }
     }
}