某笔试的题目:
锯齿数独3x3
简单来说就是给你一个填了某些字的数独,告诉你哪3个点属于一个宫,然后同行同列同宫不能有重复。
接下来给定几组数据,判断是否有解,唯一解则输出Unique和该解,多解则输出Mutiple,无解输出无解。
思路:
经典的矩阵型,dfs遍历的方式。自己写的时候遇上了几个问题,现在在此总结一下。
3行3列代表数独信息,下面3行,每行代表一个宫的三个点。
输入数据如下:
4
*2*
1*2
***
0 0 0 1 1 0
0 2 1 1 1 2
2 0 2 1 2 2
遍历的方式:使用dfs遍历,然后上下左右遍历,
如果点超过边界则返回。
如果访问过则返回。防止再次访问。
对于点有两种情况,一种是没有赋值的点,那我们就赋值,赋值时从1到3依次判断,判断该点是否满足行列宫没有重复。
已有值的点,那么无需再访问,直接返回即可。
(一开始我是这么想的,发现不能这样:原因如下:
例如:
这个左上角的点去dfs遍历时,右边和下面的点都已赋值,如果直接返回,会出现dfs直接无法遍历整个图。因为(0,0)这个点与外界不连通。因此为了实现走出外面,即使该值有点也要进行向外dfs:
这样即可保证dfs一次初始点(0,0)一定能遍历完整张图。
上面是对于该点已有值的情况,接下来介绍对于该点没有值的情况:
如果没有值就从1到3依次往里面试看是否满足同行同列同宫没有相同的数,找到第一个成功的数就填入。
填入之后则将checkNum++(checkNum是记录已经填满的数字个数)。

找到了一个点之后,我们就以此为基础,继续dfs:如下图红框所示

而当dfs结束时,也就是回溯后, 需要将值返回成原来的样子:如下图红框所示
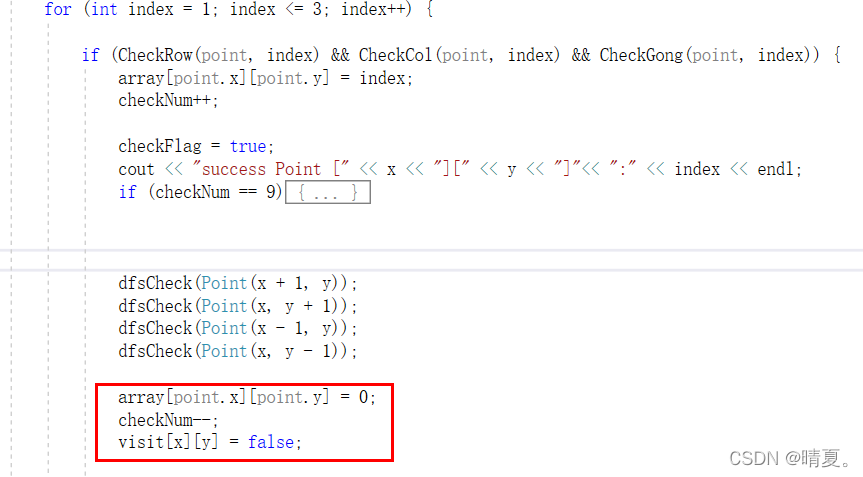
那么如何判断是否找到解?找到解之后需要做什么?
判断是否找到解的方式比较简单,只需要在填入数字,增加checkNum时,判断是否为9:
找到解后,将ans的值++。

由于单解情况下需要输出解,而回溯时会把填的数字清空,所以我们需要把该解记录下来,用一个successArray。
此处如何判断多解的思路?
此处无需找出全部解,只需要判断是否是多解即可。
因此,如果找到了一个解,那么只需要将这个解记录下来,然后之后如果找到了解(即checkNum为9)的话,就判断这两个解是否相同,如果不相同则说明有多解。

代码如下:
#include<iostream>
using namespace std;
class Point {
public:
int x, y;
Point() {
}
Point(int x1, int y1) {
x = x1, y = y1;
}
};
class GongClass {
public:
Point gongPoint[3];
};
class ShuDu {
int array[3][3];
bool visit[3][3];
GongClass Gong[3];
int checkNum = 0;//已经写完的数
int successArray[3][3];
public:
int hasAns = 0;
void ShuDuInit() {
for (int i = 0; i < 3; i++) {
for (int j = 0; j < 3; j++) {
char num;
cin >> num;
if (num != '*') {
checkNum++;
array[i][j] = int(num - '0');
}
else array[i][j] = 0;
visit[i][j]=false;
}
}
for (int i = 0; i < 3; i++) {
for (int k = 0; k < 3; k++) {
int x, y;
cin >> x >> y;
Point point;
point.x = x;
point.y = y;
Gong[i].gongPoint[k] = point;
}
}
//dfsCheck(Point(0, 0));
for (int i = 0; i < 3; i++) {
for (int j = 0; j < 3; j++) {
cout << "dfsPoint:" << i << " " << j << endl;
printArray();
dfsCheck(Point(i, j));
}
}
/*cout << checkNum << endl;
cout << hasAns << endl;*/
}
bool CheckRow(Point point, int num) {
int x = point.x;
int y = point.y;
for (int j = 0; j < 3; j++) {
if (array[x][j] == num) {
//cout << "chongfuRow" << x << " " << j << endl;
return false;
}
}
return true;
}
bool CheckCol(Point point, int num) {
int x = point.x;
int y = point.y;
for (int i = 0; i < 3; i++) {
if (array[i][y] == num) {
//cout << "chongfuCol " << i << " " << y << endl;
//cout << "array i y:"<<array[i][y] << endl;
return false;
}
}
return true;
}
bool CheckGong(Point point, int num) {
GongClass pointInGong = findGong(point);
for (int i = 0; i < 3; i++) {
int x = pointInGong.gongPoint[i].x;
int y = pointInGong.gongPoint[i].y;
if (array[x][y] == num)return false;
}
return true;
}
GongClass findGong(Point point) {
for (int i = 0; i < 3; i++) {
for (int j = 0; j < 3; j++) {
if (Gong[i].gongPoint[j].x == point.x&&Gong[i].gongPoint[j].y == point.y)
return Gong[i];
}
}
return Gong[0];
}
void dfsCheck(Point point) {
int x = point.x;
int y = point.y;
if (point.x < 0 || point.x >= 3 || point.y < 0 || point.y >= 3)return;
if (visit[x][y] == true)return;
/*if (visit[x+1][y] == false)dfsCheck(Point(x + 1, y));
if (visit[x][y+1] == false)dfsCheck(Point(x, y + 1));
if (visit[x - 1][y] == false)dfsCheck(Point(x - 1, y));
if (visit[x][y-1] == false)dfsCheck(Point(x, y - 1));*/
//cout << "point.x:" << x << " point.y:" << y << endl;
visit[x][y] = true;//进入一个点则设置访问
bool checkFlag = false;//检查是否有满足的数字可以填入
if (array[x][y] == 0) {
for (int index = 1; index <= 3; index++) {
//检查该数字是否满足每行每列每宫的要求
if (CheckRow(point, index) && CheckCol(point, index) && CheckGong(point, index)) {
array[point.x][point.y] = index;
checkNum++;
checkFlag = true;
cout << "success Point [" << x << "][" << y << "]"<< ":" << index << endl;
if (checkNum == 9) {
hasAns++;
if (hasAns > 1) {
if (checkSameArray()) {
cout << "SameArray" << endl;
hasAns--;
break;
}
}
cout << "hasAns" << endl;
//由于回溯时会删去visit的记录和做好标记的结点,所以需要删除值,但是因为需要打印,所以需要将该成功的值保存
for (int i = 0; i < 3; i++) {
for (int j = 0; j < 3; j++)
successArray[i][j] = array[i][j];
}
printArray();
}
//dfsCheck(Point(x + 1, y));
//dfsCheck(Point(x, y + 1));
//dfsCheck(Point(x - 1, y));
//dfsCheck(Point(x, y - 1));
//array[point.x][point.y] = 0;
//checkNum--;
//visit[x][y] = false;
break;
}
}
}
else {
//visit[x][y] = true;
dfsCheck(Point(x + 1, y));
dfsCheck(Point(x, y + 1));
dfsCheck(Point(x - 1, y));
dfsCheck(Point(x, y - 1));
return;
}
//如果里面不能填入数字,说明前一步有问题,因此应该要返回,并且重置访问
if (checkFlag == false) {
visit[x][y] = false;
return;
}
dfsCheck(Point(x + 1, y));
dfsCheck(Point(x, y + 1));
dfsCheck(Point(x - 1, y));
dfsCheck(Point(x, y - 1));
array[point.x][point.y] = 0;
checkNum--;
visit[x][y] = false;
return;
}
void printSuccessArray() {
for (int i = 0; i < 3; i++) {
for (int j = 0; j < 3; j++) {
cout << successArray[i][j];
}
cout << endl;
}
}
void printArray() {
for (int i = 0; i < 3; i++) {
for (int j = 0; j < 3; j++) {
cout << array[i][j];
}
cout << endl;
}
}
bool checkSameArray() {
for (int i = 0; i < 3; i++) {
for (int j = 0; j < 3; j++) {
if (array[i][j] != successArray[i][j])return false;
}
}
return true;
}
};
int main() {
int t;
cin >> t;
while (t--) {
ShuDu shuDu;
shuDu.ShuDuInit();
if (shuDu.hasAns == 1) {
cout << "Unique" << endl;
shuDu.printSuccessArray();
}
else if(shuDu.hasAns>1){
cout << "Multiple" << endl;
}
else cout << "NO"<<endl;
}
};
/*
1
*2*
1*2
***
0 0 0 1 1 0
0 2 1 1 1 2
2 0 2 1 2 2
4
*2*
1*2
***
0 0 0 1 1 0
0 2 1 1 1 2
2 0 2 1 2 2
**3
***
***
0 0 1 0 1 1
0 1 0 2 1 2
2 0 2 1 2 2
**3
1**
**2
0 0 1 0 1 1
0 1 0 2 1 2
2 0 2 1 2 2
3*3
1**
**2
0 0 1 0 1 1
0 1 0 2 1 2
2 0 2 1 2 2
*/翻转字符串
给定一个字符串,给定某个位置到某个位置,比abcdefgh,指定1~3位反转大小写,2~4位翻转大小写。
如果数据多起来,暴力法会超时。
使用差分算法。
代码如下:
差分算法思想:(174条消息) 差分数组是个啥?能干啥?怎么用?(差分详解+例题)_From now on...的博客-CSDN博客_差分数组
#include<iostream>
#include<string>
using namespace std;int main() {
string str;
cin >> str;
int times;
cin >> times;
int len = str.size();
int *array;
int *chafen;
array = new int[len + 1];
chafen = new int[len + 1];
for (int i = 0; i < len + 1; i++) {
chafen[i] = 0;
array[i] = 0;
}
while (times--) {
int left, right;
cin >> left >> right;
chafen[left]++;
chafen[right + 1]--;
}
for (int i = 1; i <= len; i++) {
array[i] = array[i - 1] + chafen[i];
//cout << array[i] << " ";
}
//cout<<endl;for (int i = 1; i <= len; i++) {
if (array[i] % 2 == 1) {
if (str[i-1] >= 'A'&&str[i-1] <= 'Z') {
str[i - 1] += 32;
}
else if (str[i-1] >= 'a'&&str[i-1] <= 'z') {
str[i - 1] -= 32;
}
}
}
cout << str;
}
腾讯2021校园招聘技术类编程题汇总
朋友圈(并查集和联通量)

输入:
2
4
1 2
3 4
5 6
1 6
4
1 2
3 4
5 6
7 8
输出:
4
2并查集的思想如下:
算法学习笔记(1) : 并查集 - 知乎 (zhihu.com)
于是可得本题代码:
#include<iostream>
#include<map>
using namespace std;
#define MAXN 100000
int fa[MAXN];
int Find(int x) {
if (x == fa[x])return x;
else {
fa[x] = Find(fa[x]);
return fa[x];
}
}
void Merge(int x, int y) {
int xFa, yFa;
xFa = Find(x);
yFa = Find(y);
fa[yFa] = xFa;
//让y的父亲变成x,也就是将y帮派融入进x的帮派
}
int main() {
int t;
cin >> t;
while (t--) {
int n;
cin >> n;
for (int i = 0; i < MAXN + 1; i++)fa[i] = i;
while (n--) {
int x, y;
cin >> x >> y;
Merge(x, y);
}
map<int, int> liantongNum;
int maxNum = 0;
for (int i = 0; i < MAXN+1; i++) {
int iFa = Find(i);
liantongNum[iFa]++;
if (maxNum < liantongNum[iFa])maxNum = liantongNum[iFa];
}
cout << maxNum << endl;
}
}
进行阶数的优化后如下:
注意不能命名为rank,否则会和系统自带的重复。
#include<iostream>
#include<map>
using namespace std;
#define MAXN 100000
int fa[MAXN+1];
int rank_[MAXN+1];
int Find(int x);
void Merge(int x, int y);
int main() {
int t;
cin >> t;
while (t--) {
int n;
cin >> n;
for (int i = 0; i < MAXN + 1; i++) {
fa[i] = i;
rank_[i] = i;
}
while (n--) {
int x, y;
cin >> x >> y;
Merge(x, y);
}
map<int, int> liantongNum;
int maxNum = 0;
for (int i = 0; i < MAXN+1; i++) {
int iFa = Find(i);
liantongNum[iFa]++;
if (maxNum < liantongNum[iFa])maxNum = liantongNum[iFa];
}
cout << maxNum << endl;
}
}
int Find(int x) {
if (x == fa[x])return x;
else {
fa[x] = Find(fa[x]);
return fa[x];
}
}
void Merge(int x, int y) {
int xFa, yFa;
xFa = Find(x);
yFa = Find(y);
if (rank_[xFa] <= rank_[yFa]) {
fa[xFa] = yFa;
}
else {
fa[yFa] = xFa;
}
if (rank_[xFa] == rank_[yFa] && x != y) {
rank_[y]++;
}
//让等级低的认等级高的为父亲
}第K小字符串


思路如下,在set中,会对加入的数据自动排序,并且字符串也可以排序,也是字典序,因此此处使用set排序。
第一思路就是我们遍历所有的字符串,将其全部加入数据,然后选取第k个大小的就可以了。
对于set,我们不需要保存那么多数据,所以每次加入数据后,如果set里的数据数量大于k,我们删除队尾数据即可(此时队里有k+1个数据,第k+1个数据肯定是没有用的,可以直接删除)
故代码如下:
#include<bits/stdc++.h>
using namespace std;
int main(){
string s;
int k;
cin>>s>>k;
set<string> result;//在该容器中本身就是有序的,就是字典序
int n = s.size();
string temp;
for(int i = 0; i< n;i++){
temp.clear();
for(int j = i; j< n;j++){
temp.push_back(s[j]);//字符串也可以压栈构建
result.insert(temp);//插入结果。
//最多存k个
if(result.size()>k) result.erase(--result.end());
}
}
cout<<*(--result.end())<<endl;
return 0;
}但是我们观察可以发现,由于子串的数量可能非常庞大,我们做一些优化。
例如我们遍历字符串的顺序是怎么遍历呢?拿abcdef来说,我们的字符串顺序是
a
ab
abc
abcd
abcde
abcdef
b
bc
bcde
……
注意到如果我们是要求第四大的数据,那么abcde和abcdef我们都不需要遍历,意味着此次遍历到这里就可以结束了,可以进入下一个字母开头的了。所以代码如下:
#include<bits/stdc++.h>
using namespace std;
int main(){
string s;
int k;
cin>>s>>k;
set<string> result;//在该容器中本身就是有序的,就是字典序
int n = s.size();
string temp;
for(int i = 0; i< n;i++){
temp.clear();
for(int j = i; j< n;j++){
temp.push_back(s[j]);//字符串也可以压栈构建
if(result.size()==k){
//本轮循环中,后面字符串肯定只会更长,所以可以break掉进入下一轮循环
if (temp>=*(--result.end())){
break;
}
//如果不进入,就证明还在前面。
}
result.insert(temp);//插入结果。
//最多存k个
if(result.size()>k) result.erase(--result.end());
}
}
cout<<*(--result.end())<<endl;
return 0;
}修改如下:,如果说容器已经获取了k个数据,此时如果该次遍历的数据比已有的数据中最大的数据(也就是此时容器的最后一个),此时无需再继续往后遍历。可以进入下一个字母开始的。

模拟队列
第一思路,使用数组,但是想到使用数组后,pop出去的话那得全队元素前移,于是想着用list,list当然可以实现。
另外一个思路,使用数组,但是有一个队头队尾的指针指向队头元素在几号即可,如果有元素pop,那么直接让那个元素后移即可。
逛街

第一个思路,双重循环:
时间复杂度O(n²)
但是会超时,通过一半的样例
首先此处要明确一点,你能不能看到左边右边的楼,和你自己所站的楼的高度是没有关系的,只看左边或者右边的楼有没有挡住后面的楼!自己所处的楼就算再高也没有用还是会被挡住!
优化:
核心思路在于,能看到的楼的数据一定是递增的,因此只需要站在某一栋楼,记住有多少栋楼是递增的即可。
对于数据从左到右遍历一次,此时视角是从右边往左看,每往右边走一步的时候,看看当前楼是不是比左边邻接的那层楼矮,
1. 如果矮说明没有遮挡关系,那么往栈里添加该楼,(栈里存放的就是当前楼的右边那一楼可以看到的左边所有的楼),然后就可以在当前楼的右边一楼添加栈的大小,此即为那一楼能看到的左边的楼数。
2.如果当前楼比左边那层楼高一点,说明发生了遮挡关系,则栈需要移出左边邻接的楼层。(由于栈是先进后出,所以此时移出左边相邻的楼层就很方便。)
并且还要循环,遍历栈,将所有遮挡的楼移除。(但要注意在栈非空的时候进行)。
因此最终代码如下:
public class Solution {
public int[] findBuilding (int[] heights) {
int n = heights.length;
int[] ans = new int[n];
LinkedList<Integer> stack1 = new LinkedList<>(), stack2 = new LinkedList<>();
Arrays.fill(ans, 1);
// 往左看,也就是要得到每个数左边有多少递增的
for(int i = 0;i < n-1;i++) {
while(!stack1.isEmpty() && heights[i] >= stack1.getFirst()) {
stack1.removeFirst();
}
stack1.addFirst(heights[i]);
ans[i+1] += stack1.size();
}
// 往右看,也就是要得到每个数右边有多少递增的
for(int i = n-1;i > 0;i--) {
while(!stack2.isEmpty() && heights[i] >= stack2.getFirst()) {
stack2.removeFirst();
}
stack2.addFirst(heights[i]);
ans[i-1] += stack2.size();
}
return ans;
}
}求字符串的全部子串
做了一题,字符串abc,求出其全部字串
a b c ab bc abc
#include<iostream>
#include<string>
using namespace std;
void fun(string str, int pos)
{
if (str.length() == 0)
return;
cout << str << " ";
//必须要理解一点,fun传进来的是哪个字符串,输出的就是哪个字符串,下面的这个步骤是用来剔除特定的位置的
for (int i = pos - 1; i >= 0; --i)
{
string tmp;
for (int j = 0; j < str.length(); ++j)
{
if (j != i)
{
tmp += str[j];
}
}
fun(tmp, i);
}
}
int main()
{
string str("abcd");
fun(str, 4);
cout << endl;
return 0;
}
贪吃的小Q


小Q的歌单
动态规划,模仿背包问题,问题简化为有x+y种物品,其中x种的容积为a,y种的容积为b,背包容积为k,问背包装满一共有多少种解法?
其实就是01背包问题,将其转化为01背包问题:
01背包问题思想如下:
咱就把0-1背包问题讲个通透! - 知乎 (zhihu.com)

上图中的代码是先遍历容量再遍历物品,事实上先遍历物品会好一点(虽然效果都一样)
// weight数组的大小 就是物品个数
for(int i = 1; i < weight.size(); i++) { // 遍历物品
for(int j = 0; j <= bagWeight; j++) { // 遍历背包容量
if (j < weight[i]) dp[i][j] = dp[i - 1][j]; // 这个是为了展现dp数组里元素的变化
else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
}
}
首先要明确,遍历是按照先物品,后从左到右计算容量去遍历的。
当容量大于当前物品的长度时便可将其加入计算,然后使用
![]()
这一行代码其实很关键,关键在于由于我们每次遍历,从i开始,而i是一个物体,代表这个物体存放与否。 然后为了实现“同样是长度为3的歌,我可以用A,可以用B可以用C”,此处是怎么实现的呢?是通过加法实现的。通过让当前值加上前一行的:

这样即可实现同样的长度,比如歌曲A有三种结果,那么歌曲B的结果应该包含歌曲A的三种结果。
而后半部分就是如果满足该位置可以放入歌曲,则该值等于上一行同样的歌曲的结果,加上现在上一行,不计算p[i]的情况数,加起来即是结果。
完整代码如下:
#include <iostream>
#include <cstring>
using namespace std;
int K, A, X, B, Y;
int dp[201][1001];
int p[201];
int main()
{
while (cin >> K)
{
cin >> A >> X >> B >> Y;
memset(dp, 0, sizeof(dp));
dp[0][0] = 1;
for (int i = 1; i <= X; i++)
p[i] = A;
for (int j = X + 1; j <= X + Y; j++)
p[j] = B;
for (int i = 1; i <= X + Y; i++) {
cout << "i:" << i << endl;
for (int j = 0; j <= K; j++)
{
if (j >= p[i])
//这其实是很关键的代码
//对于遍历的
dp[i][j] = (dp[i - 1][j] + dp[i - 1][j - p[i]]) % 1000000007;
else
dp[i][j] = dp[i - 1][j] % 1000000007;
cout << "j:" << j << " dp:" << dp[i][j]<<endl;
}
cout << endl;
}
cout << dp[X + Y][K] % 1000000007 << endl;
}
}
安排机器

输入例子:
1 2 100 3 100 2 100 1
输出
1 20006
这是一道比较有难度的题,
初始的思路如下,简单来说就是贪心算法,先对机器和任务按照时间排序,时间相同按照难度等级排序,然后接下来遍历任务,对于每一个任务,我们从时间大的机器到时间小的机器进行遍历,判断是否能有机器满足时间要求和等级要求,如果满足则将其加入。
#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;
class Machine {
public:
int time;
int level;
};
class Task {
public:
int time;
int level;
};
bool cmp1(Machine a, Machine b) {
if (a.time == b.time)return a.level >= b.level;
return a.time > b.time;
}
bool cmp2(Task a, Task b) {
if (a.time == b.time)return a.level >= b.level;
return a.time > b.time;
}
int main() {
int macNum, taskNum;
cin >> macNum >> taskNum;
Machine *mac = new Machine[macNum];
Task *task = new Task[taskNum];
for (int i = 0; i < macNum; i++) {
cin >> mac[i].time >> mac[i].level;
}
for (int i = 0; i < taskNum; i++) {
cin >> task[i].time >> task[i].level;
}
sort(mac, mac + macNum, cmp1);
sort(task, task + taskNum, cmp2);
int taskIndex = 0;
int compTask = 0;
long long sumProfit = 0;
bool *used = new bool[macNum];
for (int i = 0; i < macNum; i++)used[i] = false;
for (int taskIndex = 0; taskIndex < taskNum; taskIndex++) {
int minLevel = 101;
vector<int> useableMac;
for (int i = 0; i < macNum; i++) {
//cout << mac[i].time << " "<<mac[i].level<<" ";
if (used[i]==false&&mac[i].time >= task[taskIndex].time&&mac[i].level>=task[taskIndex].level) {
sumProfit += task[taskIndex].time * 200 + task[taskIndex].level * 3;
compTask++;
used[i] = true;
break;
}
if (mac[i].time < task[taskIndex].time)break;
}
}
cout << compTask<<" "<<sumProfit;
}
但是这样的思路会有一个问题,问题在于如果遇到这种情况:
比如机器有
2 2
100 5
90 1
90 1
80 5
如果按原先的遍历顺序 90 1这个任务就会把100 5的这个任务用掉
那接下来80 5就不能使用90 1的这个机器了
为了解决这种方案,解决方法就是每次给任务选机器的时候,首先选取任务时长中可以满足的,然后选取优先级最低的任务
而为了找到优先级最低的任务,对于每个任务就需要先遍历一遍机器,找到机器中可以满足时长要求的,然后记录下来。
至于时长则不需要考虑这个问题,因为无论是机器还是任务,都是按照时间降序的,前面优先分配的任务一定是时长大的,排在后面一定时长小,因此排在前面的有资格享有高时长,
改动如下:

思路相比之前多了一步,简单来说就是先遍历找出哪个等级是最小的,然后我们再遍历一遍,找到那个等级最小的,然后使用那一台机器即可。
#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;
class Machine {
public:
int time;
int level;
};
class Task {
public:
int time;
int level;
};
bool cmp1(Machine a, Machine b) {
if (a.time == b.time)return a.level >= b.level;
return a.time > b.time;
}
bool cmp2(Task a, Task b) {
if (a.time == b.time)return a.level >= b.level;
return a.time > b.time;
}
int main() {
int macNum, taskNum;
cin >> macNum >> taskNum;
Machine *mac = new Machine[macNum];
Task *task = new Task[taskNum];
for (int i = 0; i < macNum; i++) {
cin >> mac[i].time >> mac[i].level;
}
for (int i = 0; i < taskNum; i++) {
cin >> task[i].time >> task[i].level;
}
sort(mac, mac + macNum, cmp1);
sort(task, task + taskNum, cmp2);
int taskIndex = 0;
int compTask = 0;
long long sumProfit = 0;
bool *used = new bool[macNum];
for (int i = 0; i < macNum; i++)used[i] = false;
for (int taskIndex = 0; taskIndex < taskNum; taskIndex++) {
int minLevel = 101;
vector<int> useableMac;
for (int i = 0; i < macNum; i++) {
//cout << mac[i].time << " "<<mac[i].level<<" ";
if (used[i]==false&&mac[i].time >= task[taskIndex].time&&mac[i].level>=task[taskIndex].level) {
minLevel = min(mac[i].level, minLevel);
useableMac.push_back(i);
/*sumProfit += task[taskIndex].time * 200 + task[taskIndex].level * 3;
compTask++;
used[i] = true;
break;*/
}
if (mac[i].time < task[taskIndex].time)break;
}
//cout <<endl<< minLevel << endl;
for (int i = 0; i < useableMac.size(); i++) {
if (used[useableMac[i]] == false && mac[useableMac[i]].time >= task[taskIndex].time&&mac[useableMac[i]].level == minLevel) {
sumProfit += task[taskIndex].time * 200 + task[taskIndex].level * 3;
compTask++;
used[useableMac[i]] = true;
break;
}
}
}
cout << compTask<<" "<<sumProfit;
}但是在此之上我们可以进行优化,每次找到最小值的时候不必像上面那样再优化一次,只需要每次更新最小值时记录下最小值的index即可。
改动如下:

最终代码如下:
#include<iostream>
#include<algorithm>
using namespace std;
class Machine {
public:
int time;
int level;
};
class Task {
public:
int time;
int level;
};
bool cmp1(Machine a, Machine b) {
if (a.time == b.time)return a.level >= b.level;
return a.time > b.time;
}
bool cmp2(Task a, Task b) {
if (a.time == b.time)return a.level >= b.level;
return a.time > b.time;
}
int main() {
int macNum, taskNum;
cin >> macNum >> taskNum;
Machine *mac = new Machine[macNum];
Task *task = new Task[taskNum];
for (int i = 0; i < macNum; i++) {
cin >> mac[i].time >> mac[i].level;
}
for (int i = 0; i < taskNum; i++) {
cin >> task[i].time >> task[i].level;
}
sort(mac, mac + macNum, cmp1);
sort(task, task + taskNum, cmp2);
int taskIndex = 0;
int compTask = 0;
long long sumProfit = 0;
bool *used = new bool[macNum];
for (int i = 0; i < macNum; i++)used[i] = false;
for (int taskIndex = 0; taskIndex < taskNum; taskIndex++) {
int minLevel = 101;
int minLevelIndex;
for (int i = 0; i < macNum; i++) {
//cout << mac[i].time << " "<<mac[i].level<<" ";
if (used[i]==false&&mac[i].time >= task[taskIndex].time&&mac[i].level>=task[taskIndex].level) {
if (minLevel > mac[i].level) {
minLevel = mac[i].level;
minLevelIndex = i;
}
}
if (mac[i].time < task[taskIndex].time)break;
}
if (minLevel != 101) {
sumProfit += task[taskIndex].time * 200 + task[taskIndex].level * 3;
compTask++;
used[minLevelIndex] = true;
}
}
cout << compTask<<" "<<sumProfit;
}
雀魂启动


输入例子1:
1 1 1 2 2 2 5 5 5 6 6 6 9
输出例子1:
9
例子说明1:
可以组成1,2,6,7的4个刻子和9的雀头
输入例子2:
1 1 1 1 2 2 3 3 5 6 7 8 9
输出例子2:
4 7
例子说明2:
用1做雀头,组123,123,567或456,789的四个顺子
输入例子3:
1 1 1 2 2 2 3 3 3 5 7 7 9
输出例子3:
0
例子说明3:
来任何牌都无法和牌
思路如下,首先此处可以用map存储,最简单的就是使用数组存每张牌有多少个,然后从1到9进行遍历看看哪些牌的数量没超过4,如果没超过4则加入这个牌,然后由于胡牌的规定是有一个对子和三个刻子或顺子。也就是23333的样式
对于对子,我们可以先通过循环从前往后依次试看哪些符合对子。
对于刻子或顺子,我们需要通过递归的方式实现,在递归函数中,判断是否存在刻子或顺子,如果说找到了,则将牌的对应数量--,然后递归的调用这个函数,判断剩下的牌中是否有符合的,直到牌堆为0。
当递归到牌堆为0时,则会返回true,然后接下来则会一步步的返回回去。
如果说中间某一步递归失败了,则会继续执行循环,从前往后遍历,找遍所有看是否有刻字或顺子,如果没有则返回false。
代码如下:
#include<iostream>
#include<vector>
using namespace std;
bool isHu(int *pai);
int main() {
int *pai = new int[10];
for (int i = 0; i < 10; i++)pai[i] = 0;
int sumSolve = 0;
for (int i = 0; i < 13; i++) {
int index;
cin >> index;
pai[index]++;
}
vector<int> solve;
for (int i = 1; i <= 9; i++) {
if (pai[i] >= 4)continue;
pai[i]++;
//首先需要寻找雀头
//for (int j = 1; j <= 9; j++) cout << pai[j] << " ";
//cout << endl;
for (int j = 1; j <= 9; j++) {
if (pai[j] >= 2) {
//cout << j << endl;
pai[j] -= 2;
//如果以此作为雀头的牌可以胡,则让解++,然后跳出此次循环
if (isHu(pai)) {
sumSolve++;
solve.push_back(i);
pai[j] += 2;
break;
}
pai[j] += 2;
}
}
pai[i]--;
}
if (sumSolve == 0)cout << "0";
else {
for (auto val : solve) {
cout << val << " ";
}
}
}
bool isHu(int *pai) {
bool notPai = true;
for (int i = 1; i <= 9; i++) {
if (pai[i] > 0) {
notPai = false;
break;
}
}
if (notPai == true)return true;
//那么接下来传入的数组,里面所含义的牌的数量只可能为3的倍数
for (int i = 1; i <= 9; i++) {
if (pai[i] >= 3) {
pai[i] -= 3;
if (isHu(pai)) {
pai[i] += 3;
return true;
}
pai[i] += 3;
}
}
for (int i = 1; i <= 7; i++) {
if (pai[i] >= 1 && pai[i + 1] >= 1 && pai[i + 2] >= 1) {
pai[i]--, pai[i + 1]--, pai[i + 2]--;
if (isHu(pai)) {
pai[i]++, pai[i + 1]++, pai[i + 2]++;
return true;
}
pai[i]++, pai[i + 1]++, pai[i + 2]++;
}
}
return false;
}万万没想到之抓捕孔连顺

输入例子1:
4 3 1 2 3 4
输出例子1:
4
例子说明1:
可选方案 (1, 2, 3), (1, 2, 4), (1, 3, 4), (2, 3, 4)
输入例子2:
5 19 1 10 20 30 50
输出例子2:
1
例子说明2:
可选方案 (1, 10, 20)
输入例子3:
2 100 1 102
输出例子3:
0
例子说明3:
无可选方案
一开始自己的思路错了,一开始没有意识到,只要最右边的不同,例如:
12 4
12 5
这两种情况下,最右边的是不同的,那么前面两个的位置即使相同也没关系,然后自己因为这个思路想错了。
假如1~5都满足距离小于等于d的情况,那么此时固定住5,1~4任选两个位置都能满足情况。
有两个关键问题:
什么时候左扩?当左边的点太远时,则需要左移动。并且我们需要注意,在我们左移的时候,我们是不往res里++的!
什么时候右移,我们会一直右移,直到把所有的距离近的驱逐出去(bushi),
每右移一次,就让在左边界和右边界里任选两个,把结果加起来即可。
代码:
#include<iostream>
using namespace std;
int main() {
int n, d;
cin >> n >> d;
int *pos = new int[n];
for (int i = 0; i < n; i++)cin >> pos[i];
if (n < 3) {
cout << "0";
return 0;
}
int left = 0, right = 2;
long sum = 0;
while (right<n) {
//cout << left << " " << right << endl;
while (pos[right] - pos[left] > d) {
//cout << left << " " << right << endl;
left++;
}
long num = right - left;
long res = num * (num - 1) / 2;
sum += res;
//sum+=num-1;
sum %= 99997867;
right++;
}
cout << sum;
}实现产品经理PM的idea
#include<iostream>
#include<vector>
#include<algorithm>
#include<map>
using namespace std;
class Idea {
public:
Idea() { order = 3001, time = 3001; isStart = false; }
Idea(int order1, int time1) { order = order1, time = time1; }
int ideaIndex;//记录下这是第几个idea,以便输出时按顺序
int PMindex;//属于哪一个工作经理
int order;
int startTime;//什么时候开始的
int time;//需要多少时间完成
int compTime;
bool isStart;
};
bool PMcmp(Idea id1, Idea id2) {
if (id1.order > id2.order)return true;
else if (id1.order == id2.order) {
if (id1.time < id2.time)return true;
else if (id1.time == id2.time) {
if (id1.startTime < id2.startTime)return true;
else return false;
}
return false;
}
else return false;
}
bool proCmpTime(Idea id1, Idea id2) {
if (id1.time < id2.time)return true;
else if (id1.time == id2.time) {
if (id1.PMindex < id2.PMindex)return true;
}
return false;
}
int main() {
int PMnum, proNum, ideaNum;
cin >> PMnum >> proNum >> ideaNum;
Idea **PMidea = new Idea*[PMnum+1];
Idea *allIdea = new Idea[ideaNum];
for (int i = 0; i <= PMnum; i++) {
PMidea[i] = new Idea[3001];
}
for (int i = 0; i < ideaNum; i++) {
int PMindex, startTime, order, time;
cin >> PMindex >> startTime >> order >> time;
//Idea idea(order, time);
allIdea[i].ideaIndex = i;
PMidea[PMindex][startTime].ideaIndex = i;
PMidea[PMindex][startTime].PMindex = PMindex;
PMidea[PMindex][startTime].order = order;
PMidea[PMindex][startTime].startTime = startTime;
PMidea[PMindex][startTime].time = time;
}
/*for (int i = 1; i <= PMnum; i++) {
for (int j = 1; j <= 3000; j++) {
if (PMidea[i][j].order != 3001)
cout <<j<<" "<< PMidea[i][j].order << " " << PMidea[i][j].time << endl;
}
}*/
int *proLeaveWork = new int[proNum];//每个程序员的剩余工作时间
for (int i = 0; i < proNum; i++)proLeaveWork[i] = 0;
map<int, Idea> proDoingWork;//记录每个程序员此时正在完成哪一项工作
int doneWork = 0;
vector<Idea> pmToDoIdea[3001];
bool *proIsBusy=new bool[proNum];
for (int i = 0; i < proNum; i++)proIsBusy[i] = false;
int nowTimeToDoIdea=0;//用来记录当前时间有多少idea等待完成,仅仅是用来记录而已
for (int i = 1; i <= 4000; i++) {
//cout<< "-------------------------------" << endl;
//cout << "nowTime is :" << i << endl;
//对于每个时间点
if (doneWork == ideaNum)break;//如果已经完成所有工作则退出
//扫描每个PM在这个时间点是否有idea,如果有则加入idea的一个容器中
for (int j = 1; j <= PMnum; j++) {
if (PMidea[j][i].order != 3001) {
pmToDoIdea[j].push_back(PMidea[j][i]);
nowTimeToDoIdea++;
//cout <<i <<" pmIndex:"<<j<< " "<<PMidea[j][i].order << " " << PMidea[j][i].time << endl;
}
}
for (int j = 1; j <= PMnum; j++) {
sort(pmToDoIdea[j].begin(), pmToDoIdea[j].end(), PMcmp);//对于每个PM选出最想要实现的一个idea
}
//cout << "vec.size:" << pmIdeaVec.size()<<endl;
//for (auto val : pmIdeaVec)cout <<val.PMindex<<" "<< val.order << " " << val.time << endl;
for (int j = 0; j < proNum; j++) {
if (i != 1 && proLeaveWork[j] == 0&&proIsBusy[j]==true) {
//如果不是最开始,并且此时若已完成,则
int ideaIndex = proDoingWork[j].ideaIndex;
proDoingWork[j].compTime = i;//i代表的是当前时间,把这个idea的完成时间设定为当前的时间
//cout << i << endl;
doneWork++;
//cout <<"now programIndex:"<<j <<" compIdeaIndex:" << ideaIndex << endl;
allIdea[ideaIndex].compTime = i;
proIsBusy[j] = false;
}
if (proLeaveWork[j] > 0) {
proLeaveWork[j]--;
continue;
}
else if(nowTimeToDoIdea>0&& proLeaveWork[j] == 0){
nowTimeToDoIdea--;
//代表此时程序员有空,并且有idea可以执行
vector<Idea> pmIdeaVec;
//每一轮中,在每个PM中选取最想要的一个idea放入,
for (int k = 1; k <= PMnum; k++) {
if (pmToDoIdea[k].size() > 0)
pmIdeaVec.push_back(pmToDoIdea[k][0]);
}
//然后对时间进行排序
sort(pmIdeaVec.begin(), pmIdeaVec.end(), proCmpTime);
proLeaveWork[j] += pmIdeaVec[0].time;
proDoingWork[j] = pmIdeaVec[0];//把此时程序员正在做的工作放进map中进行记录
int PMindex = pmIdeaVec[0].PMindex;
if(pmToDoIdea[PMindex].size()>0)pmToDoIdea[PMindex].erase(pmToDoIdea[PMindex].begin());
//cout << "nowProgramm will do idea is:" << proDoingWork[j].ideaIndex << endl;
proIsBusy[j] = true;//将此时程序员设为处于忙碌的状态
proLeaveWork[j]--;
}
}
}
for (int i = 0; i < ideaNum; i++)cout << allIdea[i].compTime<<endl;
/*for (int i = 1; i <= PMnum; i++) {
for (int j = 1; j <= 3000; j++) {
if (PMidea[i][j].order != 3001)
cout << " " << PMidea[i][j].compTime << endl;
}
}*/
}分配房间

示例1
输入
3 1 6 5 1
输出
4 4 4
首先核心是找开头
一开始的思路是找到所有值中最小的,则那个即是开头,后来发现不对。
在所有最小的数据中,最接近最后那个位置的左边的,才是开头。
#include<iostream>
#include<vector>
#include<bits/stdc++.h>
using namespace std;
int main() {
int roomNum, lastPer;
cin >> roomNum >> lastPer;
int *roomPer = new int[roomNum + 1];
int minIndex = 1;
cin >> roomPer[1];
int minVal = roomPer[1];
vector<int> minIndexVec;//把所有可能是最小值的存放起来
for (int i = 2; i <= roomNum; i++) {
cin >> roomPer[i];
if (roomPer[i] < minVal) {
minVal = roomPer[i];
minIndex = i;
}
}
for (int i = 1; i <= roomNum; i++) {
if (roomPer[i] == minVal) {
minIndexVec.push_back(i);
}
}
bool findFlag = false;
for (int i = lastPer - 1; i >= 0; i--) {
if (find(minIndexVec.begin(), minIndexVec.end(), i) != minIndexVec.end()) {
minIndex = i;
findFlag = true;
break;
}
}
if (findFlag == false) {
for (int i = roomNum; i >= lastPer; i--) {
if (find(minIndexVec.begin(), minIndexVec.end(), i) != minIndexVec.end()) {
minIndex = i;
findFlag = true;
break;
}
}
}
int round = minVal;//最小的值即为总共循环的轮数
for (int i = 1; i <= roomNum; i++) {
if (i != minIndex) {
roomPer[i] -= minVal;
}
}
//这种方法是错的,这种方法是通过初始的值看看哪个最小,然后以此判定哪个是初始点
//但是事实上,如果某个点初始的值为0,那么就会同时出现多个最小的点
roomPer[minIndex] += minVal * (roomNum - 1);
if (minIndex < lastPer) {
for (int i = minIndex + 1; i <= lastPer; i++) {
roomPer[i]--;
roomPer[minIndex]++;
}
}
else if (minIndex > lastPer) {
for (int i = minIndex + 1; i <= roomNum; i++) {
roomPer[i]--;
roomPer[minIndex]++;
}
for (int i = 1; i <= lastPer; i++) {
roomPer[i]--;
roomPer[minIndex]++;
}
}
for (int i = 1; i <= roomNum; i++) {
cout << roomPer[i] << " ";
}
}但是这样会有数据过不了:

问题是出在,离最后一个位置最近的,要包括最后一个位置本身
因此这里要改:

改成i=lastPer
这时候还会有两个数据过不了,是因为需要把int型改为long型的数据:

这样就可以全部通过,最终代码:
#include<iostream>
#include<vector>
#include<bits/stdc++.h>
using namespace std;
int main() {
int roomNum, lastPer;
cin >> roomNum >> lastPer;
long *roomPer = new long[roomNum + 1];
int minIndex = 1;
cin >> roomPer[1];
long minVal = roomPer[1];
vector<int> minIndexVec;//把所有可能是最小值的存放起来
for (int i = 2; i <= roomNum; i++) {
cin >> roomPer[i];
if (roomPer[i] < minVal) {
minVal = roomPer[i];
minIndex = i;
}
}
for (int i = 1; i <= roomNum; i++) {
if (roomPer[i] == minVal) {
minIndexVec.push_back(i);
}
}
bool findFlag = false;
for (int i = lastPer ; i >= 0; i--) {
if (find(minIndexVec.begin(), minIndexVec.end(), i) != minIndexVec.end()) {
minIndex = i;
findFlag = true;
break;
}
}
if (findFlag == false) {
for (int i = roomNum; i > lastPer; i--) {
if (find(minIndexVec.begin(), minIndexVec.end(), i) != minIndexVec.end()) {
minIndex = i;
findFlag = true;
break;
}
}
}
int round = minVal;//最小的值即为总共循环的轮数
for (int i = 1; i <= roomNum; i++) {
if (i != minIndex) {
roomPer[i] -= minVal;
}
}
//这种方法是错的,这种方法是通过初始的值看看哪个最小,然后以此判定哪个是初始点
//但是事实上,如果某个点初始的值为0,那么就会同时出现多个最小的点
roomPer[minIndex] += minVal * (roomNum - 1);
if (minIndex < lastPer) {
for (int i = minIndex + 1; i <= lastPer; i++) {
roomPer[i]--;
roomPer[minIndex]++;
}
}
else if (minIndex > lastPer) {
for (int i = minIndex + 1; i <= roomNum; i++) {
roomPer[i]--;
roomPer[minIndex]++;
}
for (int i = 1; i <= lastPer; i++) {
roomPer[i]--;
roomPer[minIndex]++;
}
}
for (int i = 1; i <= roomNum; i++) {
cout << roomPer[i] << " ";
}
}比赛平分

最终代码:
从初版代码到最终通过所有用例的代码有几点需要注意:
1.一开始分类的情况分类错了,当d1+d2>done时,此时只有可能为两小中间大,没有可能是中间小两大,因为此时d1+d2的值没有可能大于done
2.一个是使用long类型才能过大数据
3.total-done-(d1+d2)然后让其%3,假如total-done-(d1+d2)为-3,那么这种情况下取余得到的值也是0,因此还要加入其值是否大于0的判定。
#include<iostream>
using namespace std;
int main() {
int t;
cin >> t;
while (t--) {
long long total, done, d1, d2;
cin >> total >> done >> d1 >> d2;
int point1, point2, point3;
if (total % 3 != 0) {
cout << "no" << endl;
continue;
}
if (d1 > total / 3 || d2 > total / 3) {
cout << "no" << endl;
continue;
}
//这种情况下,中间那个数是最大的(不可能是最小的),
if (d1 + d2 > done) {
if (d1 > d2) {
//假如中间那个数是最小的
//point1=d1,point2=0,point3=d2;
/*if (d1 + d1 - d2 == total - done) {
cout << "yes" << endl;
continue;
}*/
//假如中间那个数是最大的
//point1=0,point2=d1,point3=d1-d2
if ((total - done - (d1 + d2)) % 3 == 0) {
cout << "yes" << endl;
//cout << "111" << endl;
continue;
}
}
else {
/*if (d1 + d2 - d1 == total - done) {
cout << "yes" << endl;
continue;
}*/
if ((total - done - (d1 + d2)) % 3 == 0) {
cout << "yes" << endl;
//cout << "222" << endl;
continue;
}
}
}
//这种情况下,d1+d2<=done
else {
//中间小两头大的情况
if ((total - done - (d1 + d2)) % 3 == 0) {
cout << "yes" << endl;
//cout << "333" << endl;
continue;
}
if ((total - done - (d1 + d2 + d2)) >= 0 &&(total - done - (d1 + d2 + d2)) % 3 == 0) {
//cout << "total-done:"<<total - done<<endl;
//cout << "d1+d2+d2:"<<d1 + d2 + d2 << endl;
cout << "yes" << endl;
//cout << "444" << endl;
continue;
}
if ((total - done - (d1 + d2 + d1)) % 3 == 0) {
cout << "yes" << endl;
//cout << "555" << endl;
continue;
}
}
cout << "no" << endl;
}
}100个人开始,依次报数,留下偶数,淘汰奇数,重复此过程,问最后留下的人在第一轮是几号

买股票(可重复购买)

对于每天有三种状态,要么买,要么不买,要么卖出,就这三种选择,因此可以使用暴力递归:(大概能通过百分60的样子)
#include<iostream>
using namespace std;
int day;
int *price;
int maxMoney = 0;
void dfs(int dayIndex, int money,int gupiaoNum) {
cout << "dayIndex:" << dayIndex << " money:" << money << " gupiaoNum:" << gupiaoNum << endl;
if (dayIndex == day-1) {
money += gupiaoNum* price[dayIndex];
if (maxMoney < money)maxMoney = money;
return;
}
//买股票
if(money>=price[dayIndex])dfs(dayIndex + 1, money - price[dayIndex], gupiaoNum + 1);
//什么也不做
dfs(dayIndex + 1, money, gupiaoNum);
if(gupiaoNum>0)dfs(dayIndex + 1, money + price[dayIndex], gupiaoNum - 1);
}
int main() {
int money;
cin >> day >> money;
price = new int[day];
for (int i = 0; i < day; i++) {
cin >> price[i];
}
dfs(0, money, 0);
cout << maxMoney << endl;
}
//6 2
//2 3 1 1 1 2
//5 10
//5 4 3 2 1
如果使用动态规划,注意一下,来对比下力扣的股票动态规划题:
那几道题都有个特点,是股票最多只能持有一只,而本题不同,本题的股票可以同时持有多只,那要怎么规划呢?
注意下力扣的股票动态规划题,力扣股票题的dp值代表的是当前所能获得的最大钱,而本题中的dp值并不是所能获得的最多钱,而是最多的现金。
那么问题在于,怎么求出最后一天的总资产什么时候最大呢?
总资产中由股票最后卖出去的钱由股票的钱和现金所决定。而股票的钱只取决于最后一天的股票数量!
由于资产有股票和现金这两部分所决定,是两个都在变化的量,那么做法是:
对于第i天,我们找出其持有0~j只股票的最大现金数量,然后找到最大的即可。
即例如第i天,我拥有的最多的钱,要么是持有0只股票+现金,要么是1只股票+现金……要么是i只股票+现金(每天最多一个股票,i天最多i个股票),其中和最大的即是解。
第i天持有j只股票的状态转移方程为dp[i][j]=max(
dp[i-1][j] 什么也不做
,dp[i-1][j+1]+price[i] 今天卖掉股票
dp[i-1][j-1]-price[i] 今天买入股票
这三种情况组成
对于本题在填充动态规划的表格时,第一行需要初始化,而第一列不需要初始化,因为这个填表是这样的:
第一列的转移来源如红色所示,任意列的转移来源如黄色所示,最后一列的转移来源如最后一列所示。

对于非法的数据,事实上,这些都是非法的:第i天不可能拥有i+1个股票。

但是我们无需对其初始化,我们只需要初始化第一行就行了,因为后续的行会由于上面数据的非法而下面也会跟着非法。
于是最终代码如下:
注意下标,为了方便看图,因为没有第0天,所以舍弃掉第一行
而股票数量j,是可以有0的,所以不舍弃掉第0列,j就从0开始。
这样方便对照表格的下标,不用去思考此处需要加一还是减一。
#include<iostream>
using namespace std;
int **dp, *price;
int max(int a, int b) {
if (a > b)return a;
else return b;
}
int maxThree(int a, int b, int c) {
return max(a, max(b, c));
}
int main() {
int n, money, i, j;
cin >> n >> money;
price = new int[n + 1];
dp = new int*[n+1];
for (int i = 0; i <= n; i++)dp[i] = new int[n+1];
for (i = 1; i <= n; i++)cin >> price[i];
//cout << "11";
for (int j = 2; j <= n; j++) {
dp[0][j] = INT_MIN;//第i天不可能拥有i+1只股票
}
//这里错写为dp[0][0],事实上,既然把下标后移了一位,那么初始化第一天应该是对应下标dp[1][0]
dp[1][0] = money;
if (price[1] <= money)dp[1][1] = money - price[1];
else dp[1][1] = INT_MIN;
//为什么是从2开始?因为第一天是自己初始化了,第二天再按顺序初始化
for (int i = 2; i <=n ; i++) {
//cout << i << endl;
for (int j = 0; j <= n; j++) {
if (j == 0) {
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j + 1] + price[i]);
}
else if (j == n) {
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - 1] - price[i]);
}
else {
dp[i][j] = maxThree(dp[i - 1][j], dp[i - 1][j + 1] + price[i], dp[i - 1][j - 1] - price[i]);
}
}
}
int res = 0;
//for (int i = 0; i <= n; i++) {
// for (int j = 0; j <= n; j++) {
// cout << dp[i][j] << " ";
// }
// cout << endl;
//}
for (int j = 0; j <= n; j++) {
res = max(res, dp[n][j]+price[n]*j);//不要忘记还要加上当天的股票价格
}
cout << res;
}
删除非质数位数组

本来以为需要找什么规律,后面发现直接暴力输出就行…
或者可以用打表找规律的方法。


























 660
660

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








