第六讲 中值定理
介值定理


导数介值定理

证明:

与函数的介值定理不同,函数的介值定理要求函数连续,但是在这里,只需要满足:

这一点即可。
这是因为

如果一个函数可导,那么这个导函数不可能存在跳跃间断点。
也不会存在可去间断点和无穷间断点(但是有可能会有振荡间断点,但是不会违背导数介值定理)

(因为即使是振荡间断点,也可以取得-1到1所有的值,因此不会违背导数介值定理)
平均值定理

例题:


看到多个相加的 用平均值定理,加起来除以个数。然后再用罗尔定理

积分中值定理还可以理解为平均值定理

费马定理


证明过程:
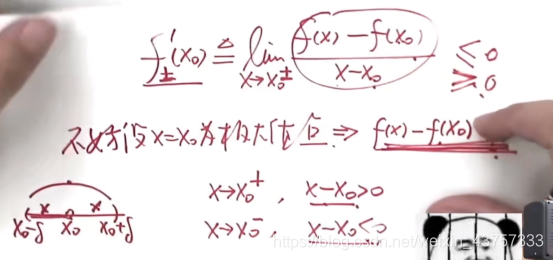

如果表达式大于或小于零 并且极限存在 则根据极限的保号性定理 极限的符号就等于表达式的符号

看到导数想到用定义,定义写出来后可以发现f(x)不是在端点而是在区间内取得最大值,说明存在极值,则可以用费马定理
由此可以引申出这样的一个结论:

罗尔定理


推广的罗尔定理可以直接使用
因此 证明某点导函数值为零可以有以下的思路:

除了这种考法,还有另外的考法:
构造辅助函数

例如:



对于1.6.6

应该把1移过去
然后可以发现

再例如

通用法则

例如1.6.6:

1.6.3:

第一种方法:
可以从需要证明的东西出发:

例如这个

移项后 构造
其实看到这个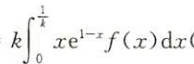 可以想到积分中值定理(也就是平均值定理)
可以想到积分中值定理(也就是平均值定理)
第二种方法:
出题人所给的提示就是 这个东西
这个东西
因此这里可以构造函数:

令F(X)就等于这个
然后其实这两种方法只差了一个常数:

而常数对于求导来说没什么区别
1.6.6

在证第二问的时候遇到了困难,这时候困难就需要用到第一问的结论

另外一种考法,多次使用罗尔定理:

在上图 三次使用了罗尔定理:三点相同,就可以证二阶导等于零
例题:

需要用到的知识:
我们需要证明这个:
根据下节的拉格朗日:

题目又给了积分: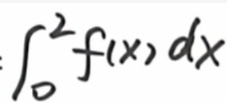
已知变限积分:

因此见到定积分想到这两种:

想到可以用拉格朗日:

但是总结下来可以知道第一问可以直接使用平均值定理:


第二问

同样用平均值定理
这样就可以得到三个相等的点,就可以使用过罗尔定理了
然后使用三次罗尔定理
罗尔定理的难点在于构造函数和找相同的点
拉格朗日中值定理


特殊的0和1:
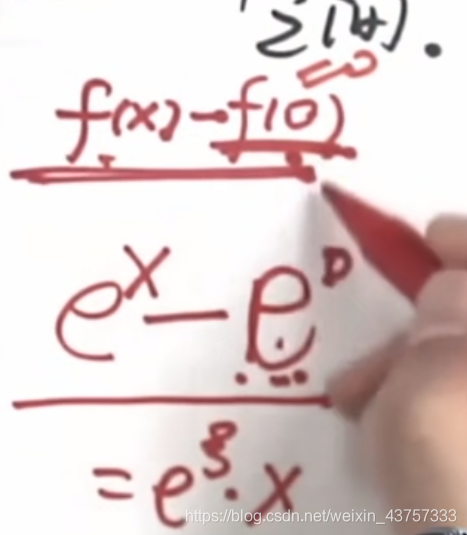


因此,上面那题的那一问还可以这样写:




观察这题所要证明的东西可以看到与罗尔定理有类似之处,说下区别:
首先拉格朗日可以推罗尔:

如果要证导数=0用罗尔,如果要证一阶导数等于一个函数值用拉格朗日
多次使用拉格朗日

证明两个不同的值相等的时候,不能在一个区间内使用拉格朗日,因为如果在一个区间内使用拉格朗日会导致两个值可能是相同的。此时需要划分区间,然后在不同的区间使用。

然后对其取倒数后可得:

那么接下来需要证明:

所以接下来只要取f(τ)=1/2即可
而根据介值定理 一定存在τ属于(0,1)使得f(τ)=1/2
所以如果是考研题会有个第一问:

柯西中值定理

(柯西不是由两次拉格朗日除法得出的)
另外 柯西中值定理考的较少
33年只有2000考过一次
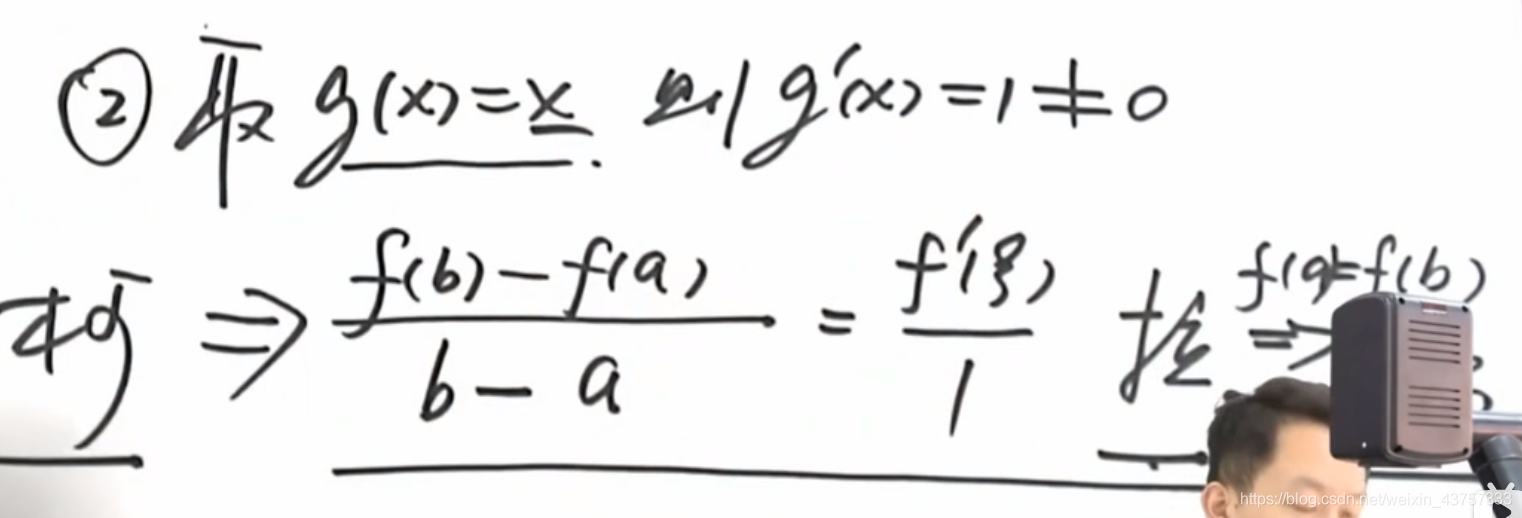
柯西取g(x)=x可以推出拉格朗日
拉格朗日取f(a)=f(b)可以推出罗尔定理
(正好柯西的老师是拉格朗日,拉格朗日老师是罗尔,一代一代发扬光大tql)
例题:

泰勒公式





说到区间时用拉格朗日,说到极限时可用佩亚诺余项
并且还需要注意这两个定理成立的条件:

例题:

接下来看这题的第二问:

看到所要证明的东西中有积分和对称区间,我们联想到:
首先对于积分形式 有这样的一个关系:奇函数在对称区间积分和为零)

接下来在第一问的基础上,两边取积分:


接下来其实最关键的一步 就是用有界最值定理了




1和2的联系:积分
2和3的联系:拉格朗日
2和4的联系:泰勒
























 974
974

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








