路径规划——搜索算法详解（一）：Dijkstra算法详解与代码

小陈最爱学习了

已于 2024-03-23 12:47:27 修改

阅读量1.1k

点赞数 32

文章标签：算法

于 2024-03-22 16:26:39 首次发布

本文链接：https://blog.csdn.net/weixin_43793717/article/details/136908204

版权

前言：

本文为小陈同学原创，本人为路径规划方向的研狗一枚，转载请阅读文末的“授权说明”，学习笔记为连载，不定期分享路径规划的知识，欢迎转载、关注、点赞👍 ！

纠结了很久还是打算做这个系列，给自己的研究生研究内容做一个总结，该系列将分为三大部分，分为搜索算法篇、路径优化篇、控制基础篇，希望对刚入门这一研究方向的朋友有所帮助！废话不多说，直接上干货。

首先，路径规划算法可以被简单地分为前端路径搜索与后端轨迹优化两个部分，路径搜索算法可以分为两大类——基于采样的路径搜索算法（如RRT、PRM）、基于图搜索的路径搜索算法（如Dijkstra、A*等），本篇将从零介绍Dijkstra算法。

Dijkstra算法解决的问题是从点A到点B的最短路径的求解，其是贪心算法的典型代表，时间复杂度为O(n2)。

一、算法过程讲解与案例分析

借鉴B站视频案例讲解：【算法】最短路径查找—Dijkstra算法_哔哩哔哩_bilibili

1. 初始化：

如下图所示，起点为A，其余B-G为未探索节点，目标点为G，点与点之间的连线标注数字为该路径的代价，在现实问题中物理意义可能是两点之间的距离，用来衡量点之间的成本信息。同时定义两个列表——L为当前路径列表，存储每一步骤中所选择的最优路径点，而X为待选择路径点列表，存储未搜索的的路径点信息。对于每一个路径点记录着两个数据：距离起始点的最小距离、上一个路径点，初始化最小距离均为无穷大，初始化上层节点为空，每一步实时更新，初始化时将起点加入路径点，由于起点距离本身长度为0，起点本身就为上层节点，所以此时记为A(0,A)。

2.更新当前点的连接点与起点的距离与上一路径点（2、3步骤为第一轮循环）：

更新当前点所连接路径点的代价，可以看到与当前所在点（蓝色）A连接的路径点（红色）有B、C，从起点A到B、C的距离分别为5 < ∞、8 < ∞，上一节点为A，故此时将X列表中的B(∞, )、C(∞, )分别更新为B(5,A)、C(8,A)。

3. 选择路径点：
在X列表中，悬着代价最小的路径点加入到路径列表L中，作为下一路径点：

4. 更新当前点的连接点与起点的距离与上一路径点（4、5步骤为第二轮循环）：

与B相连接的点有三个分别为E、D、C，其中从A经过B到达E、D两个点的距离分别为5+7=12、5+6=11，均小于正无穷，故更新，而C点处经过B到达A的距离为15>8故不更新：

5. 选择路径点：

6. 更新当前点的连接点与起点的距离与上一路径点（6、7步骤为第三轮循环）：

D经过C到达A的距离为16>11故不更新，而F为8+2=10故更新：

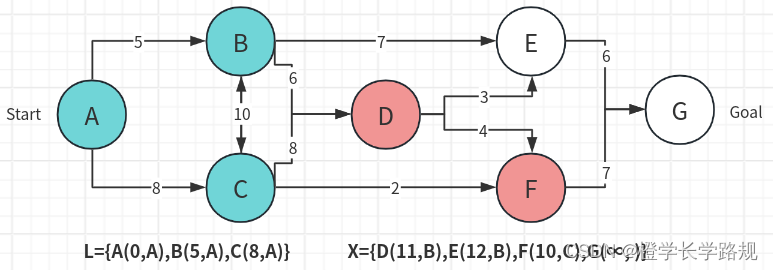
7. 选择路径点：

选择代价最小的F点加入到L列表中

8. 更新当前点的连接点与起点的距离与上一路径点（8、9步骤为第四轮循环）：

由于与F点相连接的点只有目标点G，此时更新G

9. 选择路径点：

此时代价最小的为D点，故将D加入L列表中：

10. 更新当前点的连接点与起点的距离与上一路径点（10、11步骤为第五轮循环）：

只有E与D相连，此时E通过D连接A的长度为11+3>12故不更新：

11.选择路径点：

此时代价最小的为E点，将其加入到L列表中：

12. 更新当前点的连接点与起点的距离与上一路径点（12、13步骤为第六轮循环）：

此时通过E连接G的代价为12+6=18 > 17，故不更新代价与上一路径点：

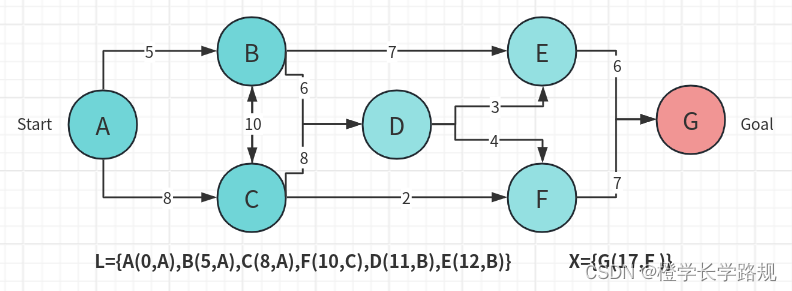
13. 此时将G加入到L列表中，此时目标点加入到L中，搜索结束：

从搜索结果L中，我们可以得到最小搜索距离为17，搜索回溯为G -> F -> C -> A，故A到G最短路径为A -> C -> F -> G：

至此，搜索完成。

二、代码部分（C++）

搞清楚了上面的理论思想，代码写了一个比较简单的版本，没有加回溯，直接编译运行就好，笔者已经将其上传到本人的github上，需要的朋友自取哈：GitHub - Adamaser/Path-Planning

#include <iostream>
#include <vector>
#include <limits>

using namespace std;

// 定义一个表示图的邻接矩阵的结构
const int INF = numeric_limits<int>::max();
typedef vector<vector<int>> Graph;

// Dijkstra算法的实现
vector<int> dijkstra(const Graph& graph, int start) {
    int n = graph.size();
    vector<int> dist(n, INF); // 初始距离设为无穷大
    vector<bool> visited(n, false); // 标记节点是否已被访问

    dist[start] = 0; // 设置起始节点距离为0

    for (int i = 0; i < n - 1; ++i) {
        // 选取未访问的距离最小的节点
        int minDist = INF, minIndex = -1;
        for (int j = 0; j < n; ++j) {
            if (!visited[j] && dist[j] < minDist) {
                minDist = dist[j];
                minIndex = j;
            }
        }

        if (minIndex == -1)
            break;

        // 标记节点已访问
        visited[minIndex] = true;

        // 更新与该节点相邻的节点的距离
        for (int j = 0; j < n; ++j) {
            if (!visited[j] && graph[minIndex][j] != INF && dist[minIndex] + graph[minIndex][j] < dist[j]) {
                dist[j] = dist[minIndex] + graph[minIndex][j];
            }
        }
    }

    return dist;
}

int main() {
    // 举例一个简单的图
    Graph graph = {
        {0, 1, 4, INF, INF},
        {1, 0, 4, 2, 7},
        {4, 4, 0, 3, INF},
        {INF, 2, 3, 0, 4},
        {INF, 7, INF, 4, 0}
    };

    // 调用Dijkstra算法计算从节点0出发到其他节点的最短路径
    vector<int> shortestDistances = dijkstra(graph, 0);

    // 输出结果
    cout << "Shortest distances from node 0:" << endl;
    for (int i = 0; i < shortestDistances.size(); ++i) {
        cout << "Node " << i << ": " << shortestDistances[i] << endl;
    }

    return 0;
}