矩阵求导简析

最新推荐文章于 2022-03-29 13:54:44 发布

西部小狼_

最新推荐文章于 2022-03-29 13:54:44 发布

阅读量1.3k

点赞数 6

文章标签：矩阵求导

本文链接：https://blog.csdn.net/weixin_43795395/article/details/84498269

版权

大家好，这是我的第一篇博客。

矩阵求导（Matrix Derivation，或者Matrix Differential），在机器学习、图像处理、最优化领域经常会遇到。其本质是多元变量的微积分，只是把求导应用在了矩阵上，不同在于这些求导是按照一定规则排列的。因此，说简单也很简单，在矩阵理论的书籍中一般会介绍雅克比（Jacobi）矩阵，点到为止，也不会详细讨论。但是这个小问题有时遇到了还是会有所疑惑，可能你会发现同一求导在不同的资料中结果不一样。关于这一方面，网上的资料略混乱，没有抓住重点，因此这里作简要总结，一些基本公式会给出简单的推导，希望对你有帮助。

布局（Layout）

首先，介绍一个重要的概念——布局。求导最简单的是标量，然后是向量和矩阵求导。所有我们把dY/dX，看做两部分-分子和分母，按照每一部分对应三种类型（标量、向量、矩阵），那么就会有9种组合，但是常用的不多，比如较常见的分母和分子都是向量。如果向量求导掌握了，那么复杂一点的矩阵求导你只需拆解为向量就可以了。因为同一个求导可以有不同的写法，所以就有了布局约定（layout conventions），分为两种：1）分子布局，numerator layout；2）分母布局，denominator layout。举个例子，向量 $Y=\begin{bmatrix} y_{1} & y_{2} & y_{3} \end{bmatrix}^{T}$ 关于向量 $X=\begin{bmatrix} x_{1} & x_{2} \end{bmatrix}^{T}$ 求导，注意这两个都是列向量：

1）按照分子布局，也就是按照y的布局，其结果为

$\frac{\partial Y}{\partial X}=\begin{bmatrix} \frac{\partial y_{1}}{\partial x_{1}} & \frac{\partial y_{1}}{\partial x_{2}} \\ \frac{\partial y_{2}}{\partial x_{1}} & \frac{\partial y_{2}}{\partial x_{2}} & \\ \frac{\partial y_{3}}{\partial x_{1}} & \frac{\partial y_{3}}{\partial x_{2}}& \end{bmatrix}$

2）按照分母布局，即按照X的布局，结果为

$\frac{\partial Y}{\partial X}=\begin{bmatrix} \frac{\partial y_{1}}{\partial x_{1}} & \frac{\partial y_{2}}{\partial x_{1}} &\frac{\partial y_{3}}{\partial x_{1}} \\ \frac{\partial y_{2}}{\partial x_{2}} & \frac{\partial y_{2}}{\partial x_{2}} & \frac{\partial y_{3}}{\partial x_{2}} \\ \end{bmatrix}$

对比以上结果，分子布局指结果与分子保持一致，以分子为主序，也就是说分子原来有3行，求导结果就有3行，每一行和分子中的每一行对应；同理，分母布局与分母保持一致，求导结果维数为：分子维数*分母维数。理解了这个概念后，那基本上矩阵求导就无所遁形了，对于复杂的矩阵可看做由行向量组成，逐步求导。

下面将列举几个常见的例子。

实例

（1） $\frac{\partial AX}{\partial X}$ , 其中 $A= \begin{bmatrix} a_{11} &a_{12} &\cdots & a_{1n}\\ \vdots & & &\vdots \\ a_{m1}&a_{m2} & \cdots & a_{mn} \end{bmatrix}$ $X=\begin{bmatrix} x_{1}\\ \vdots \\ x_{n} \end{bmatrix}$

这个式子可以说是最基本的，但是结果有两种形式，分别是 $A$ 和 $A^{T}$ ，差一个转置。首先

$AX= \begin{bmatrix} a_{11}x_{1}+a_{12}x_{2}+\cdots +a_{1n}x_{n} \\ \cdots\\ a_{m1}x_{1}+a_{m2}x_{2}+\cdots +a_{mn}x_{n} \end{bmatrix}$ ，

如果按照分子布局计算，记 $b_{i}$ 是 $AX$ 的行向量，则

$\frac{\partial AX}{\partial X}=\begin{bmatrix} \frac{\partial b_{1}}{\partial x_{1}} & \frac{\partial b_{1}}{\partial x_{2}} & \cdots & \frac{\partial b_{1}}{\partial x_{n}}\\ \vdots & & &\vdots \\ \frac{\partial b_{m}}{\partial x_{1}}&\frac{\partial b_{m}}{\partial x_{2}} & \cdots & \frac{\partial b_{m}}{\partial x_{n}} \end{bmatrix}= \begin{bmatrix} a_{11} & a_{12}& \cdots &a_{1n}\\ \vdots & & &\vdots \\ a_{m1}&a_{m2} & \cdots & a_{mn} \end{bmatrix}=A$

如果按照分母布局计算，则

$\frac{\partial AX}{\partial X}=\begin{bmatrix} \frac{\partial b_{1}}{\partial x_{1}} & \frac{\partial b_{2}}{\partial x_{1}} & \cdots & \frac{\partial b_{m}}{\partial x_{1}}\\ \vdots & & &\vdots \\ \frac{\partial b_{1}}{\partial x_{n}}&\frac{\partial b_{2}}{\partial x_{n}} & \cdots & \frac{\partial b_{m}}{\partial x_{n}} \end{bmatrix}= \begin{bmatrix} a_{11} & a_{21}& \cdots &a_{n1}\\ \vdots & & &\vdots \\ a_{1n}&a_{2n} & \cdots & a_{mn} \end{bmatrix}=A^{T}$

（2） $\frac{\partial X^{T}AX}{\partial X}$ ，其中 $A=\begin{bmatrix} a_{11} & \cdots &a_{1n} \\ \vdots & & \vdots \\ a_{n1}& \cdots &a_{nn} \end{bmatrix}$ $X=\begin{bmatrix} x_{1}\\ \vdots \\ x_{n} \end{bmatrix}$

可设 $A=\begin{bmatrix} \beta _{1}\\ \vdots \\ \beta _{n} \end{bmatrix}=\begin{bmatrix} \alpha _{1} & \cdots & \alpha _{n} \end{bmatrix}$

$X^{T}AX= \left ( x_{1} \right \cdots x_{n} )\begin{bmatrix} a_{11} &\cdots & a_{1n}\\ \vdots & & \vdots \\ a_{n1}&\cdots & a_{nn} \end{bmatrix}\begin{pmatrix} x_{1}\\ \vdots \\ x_{n} \end{pmatrix}=\sum_{i,j=1}^{n}a_{ij}x_{i}x_{j}$

所以

$\frac{\partial X^{T}AX}{\partial X}=\frac{\partial\sum a_{ij}x_{i}x_{j} }{\partial X}= \begin{bmatrix} \frac{\partial\sum a_{ij}x_{i}x_{j} }{\partial x_{1}}\\ \vdots \\ \frac{\partial\sum a_{ij}x_{i}x_{j} }{\partial x_{n}} \end{bmatrix}=\begin{bmatrix} a_{11}x_{1}+a_{12}x_{2}+\cdots +a_{1n}x_{n} +a_{11}x_{1}+a_{21}x_{2}+\cdots a_{n1}x_{n}\\ \vdots \\ a_{n1}x_{1}+a_{n2}x_{2}+\cdots +a_{nn}x_{n} +a_{1n}x_{1}+a_{2n}x_{2}+\cdots a_{nn}x_{n} \end{bmatrix}$

$=\begin{bmatrix} \beta _{1}X+\alpha _{1}^{T}X\\ \vdots \\ \beta _{n}X+\alpha _{n}^{T}X \end{bmatrix}= \begin{bmatrix} \beta _{1}+\alpha _{1}^{T}\\ \vdots \\ \beta _{n}+\alpha _{n}^{T} \end{bmatrix}X = \left \{ \begin{bmatrix} \beta _{1}\\ \vdots \\ \beta _{n} \end{bmatrix}+ \begin{bmatrix} \alpha _{1}^{T}\\ \vdots \\ \alpha _{n}^{T} \end{bmatrix}\right \}X= \left ( A+A^{T} \right )X$

上述求导过程可以看出采用的是分母布局。因此若采用分子布局，会得到另一个结果 $X^{T}(A+A^{T})$ ，这里你可以自己证明。

（3）另外矩阵求导往往也和矩阵的迹联系在一起，这里附赠一个关于迹的公式推导，对于很多关于迹的求导也许会有启发。

证明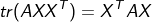： $tr(AXX^{T})=X^{T}AX$

首先 $X^{T}AX=\sum_{i,j}^{n}a_{ij}x_{i}x_{j}$ , 而

得证。

总结

在很多时候你可能常见到以下的结论，实际上这些结果都是基于分母布局而得到的。

但是，如果你观察下面这个Jacobi矩阵的形式，我们可以说是基于分子布局的，这里分子分母都是列向量，之所以分母会写成转置的形式（有时候不加转置），这样显得更不容易产生歧义，因为无论是哪一种布局似乎都是对的，其中分子主序作行，分母主序作列。

最后，如果你觉得这些不够用，你可以查看以下博客，有更全面的公式。

https://blog.csdn.net/daaikuaichuan/article/details/80620518

https://blog.csdn.net/yc461515457/article/details/49682473

西部小狼_

关注

6
点赞
踩
12

收藏

觉得还不错? 一键收藏
0
评论
矩阵求导简析

大家好，这是我的第一篇博客。矩阵求导（Matrix Derivation，或者Matrix Differential），在机器学习、图像处理、最优化领域经常会遇到。其本质是多元变量的微积分，只是把求导应用在了矩阵上，不同在于这些求导是按照一定规则排列的。因此，说简单也很简单，在矩阵理论的书籍中一般会介绍雅克比（Jacobi）矩阵，点到为止，也不会详细讨论。但是这个小问题有时遇到...
复制链接

扫一扫