机器学习入门
深度学习和机器学习?
深度学习在某种意义上可以认为是机器学习的一个分支,只是这个分支非常全面且重要,以至于可以单独作为一门学科来进行研究。
回忆知识

求解S.
对数函数的上升速度
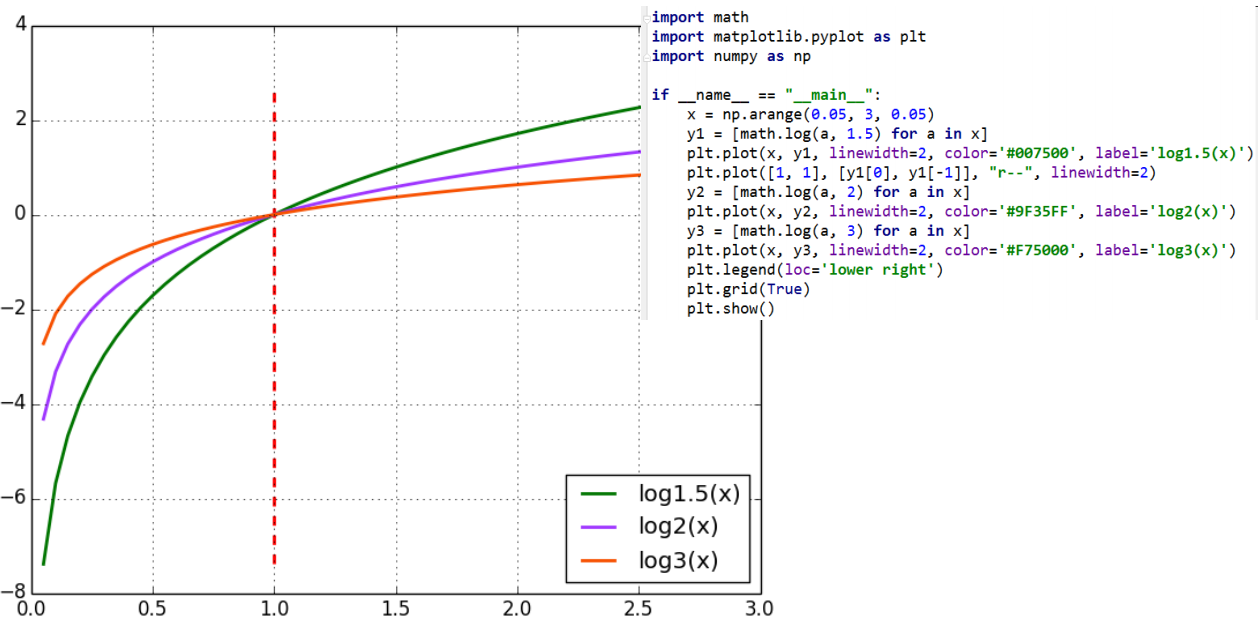
我们使用Python简单写一段代码可以很容易获得结果。但是我们使用数学来分析:
令$f(x)=log_ax$
则:
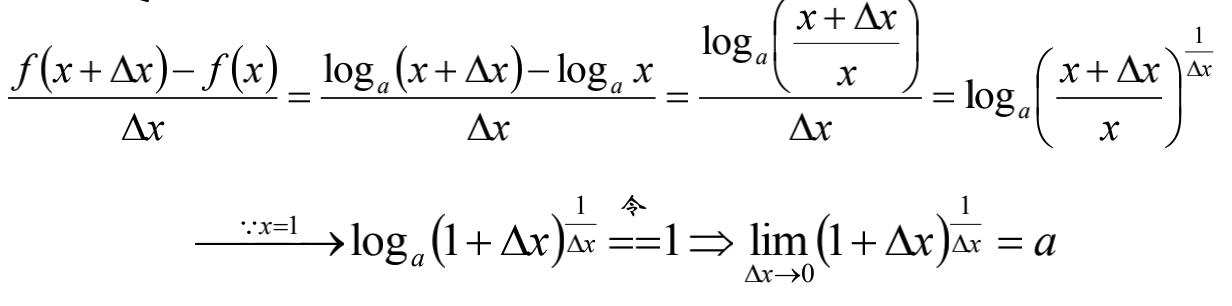
那么我们需要考虑:
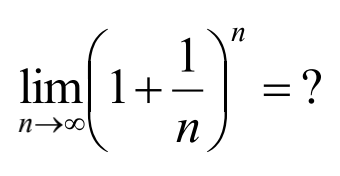
构造数列:
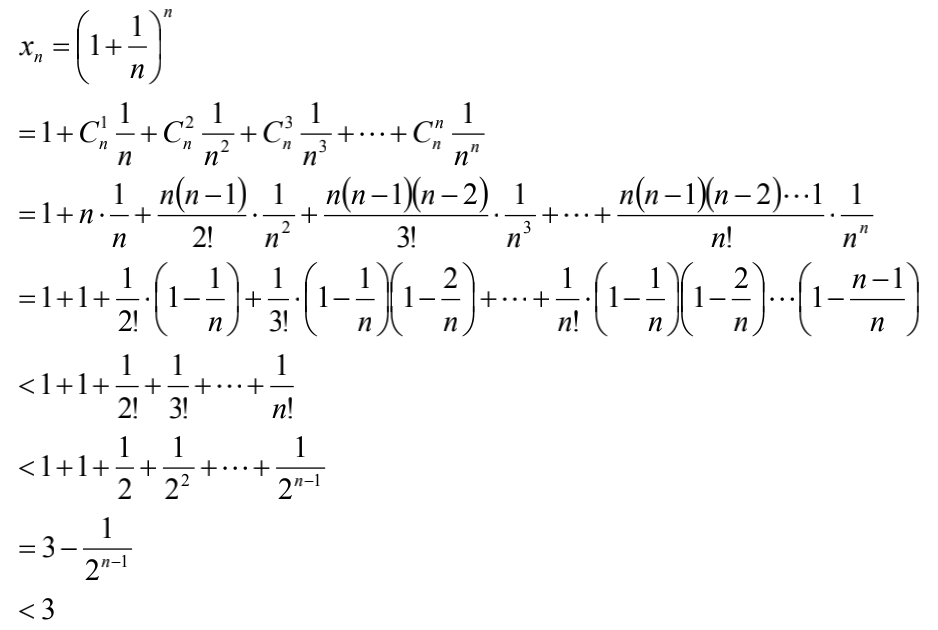
我们很容易推出:
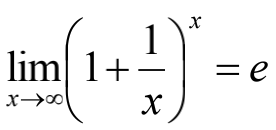
根据前文,已经证明了数组${a_n}$单增有上界,因此,必有极限,记作e。
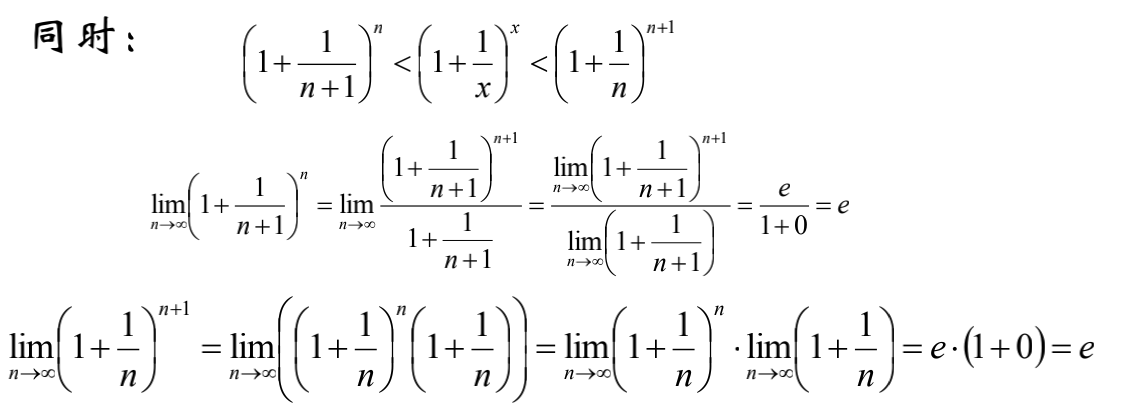
根据夹逼定理,函数
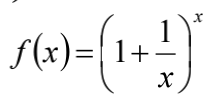
导数
- 简单来说,导数就是曲线的斜率,是曲线变化快慢的反应
- 二阶导数是斜率变化快慢的反应,表征曲线凹凸行
- 二阶导数连续的曲线,往往称之为“光顺”的
- 根据
可以得到函数$f(x)=lnx$的导数,进而进一步通过换底公式,反函数求导等,得到其他初等函数的导数
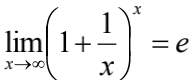
常用函数的导数
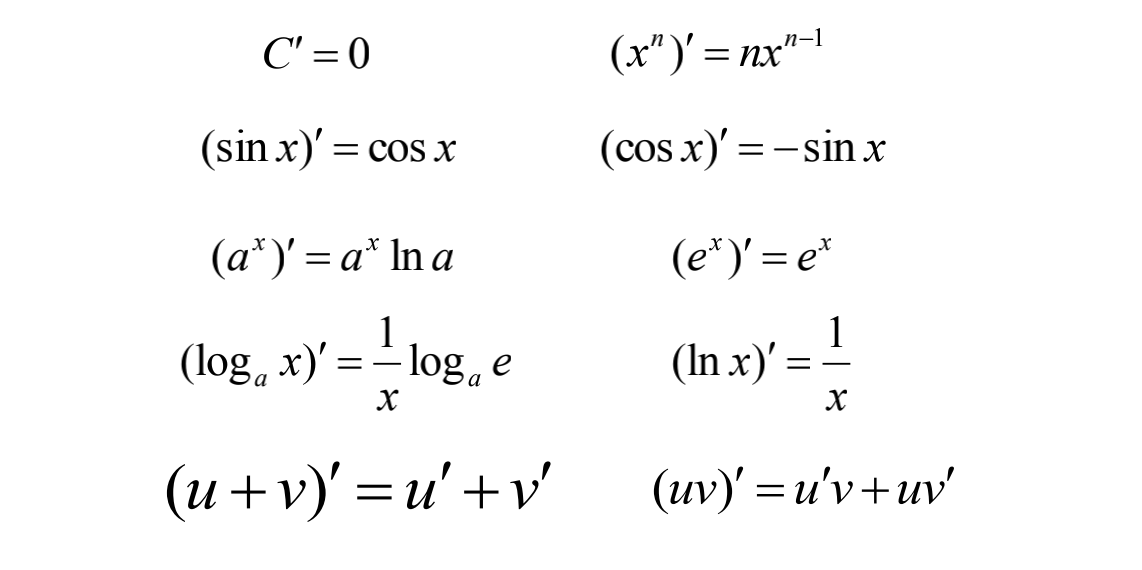
应用1
已知函数$f(x)=x^x,x>0$,
求f(x)的最小值
此处直接求导并不合适,我们可以取对数在求导。
$N^{\frac{1}{log_2N}}$=?
在计算机算法跳跃表Skip List的分析中,用到了该常数。
背景:跳表是支持增删改查的动态数据结构,能够达到与平衡二叉树、红黑树近似的效率,而实现代码简单
求解:
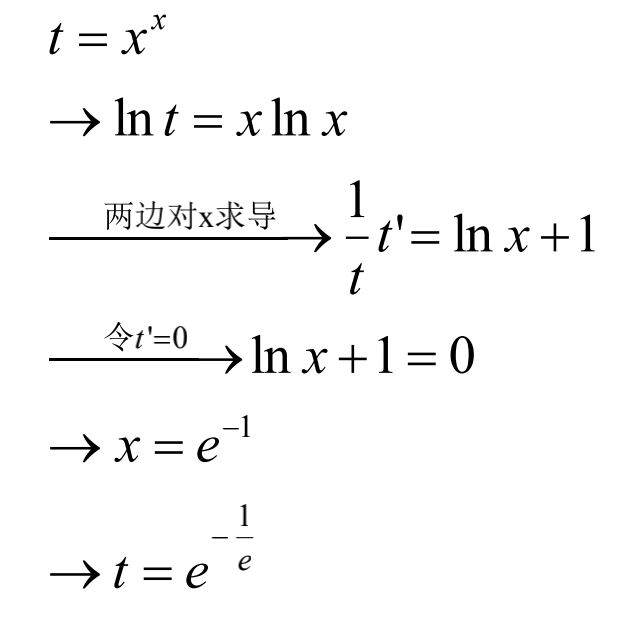
积分应用2
证明:
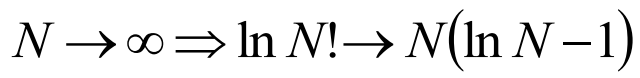
在算法复杂度分析中,任何一种关键字比较的排序算法时间复杂度为$NlgN$,可由上式推出。
解:$\ln N!=\sum{i=1}^{N}\ln i\approx \int{1}^{N}\ln xdx$
我们采用分部积分法:
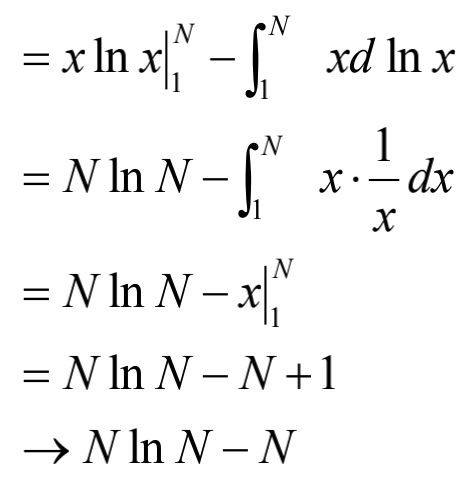
Taylor公式-Maclaurin公式
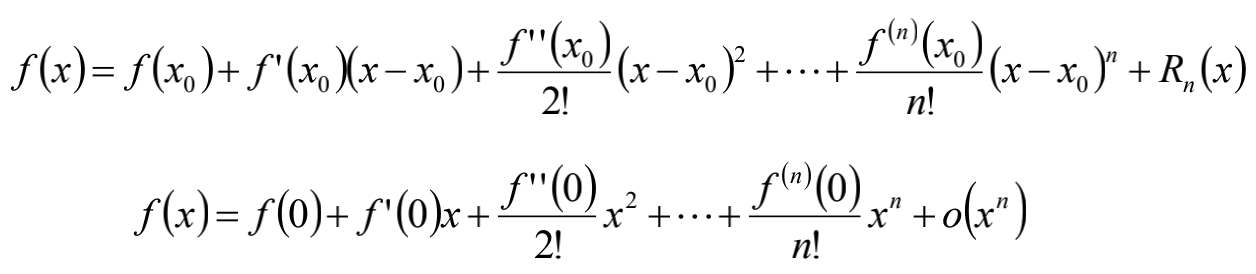
Taylor公式应用1
数值计算:初等函数值的计算(在原点展开)
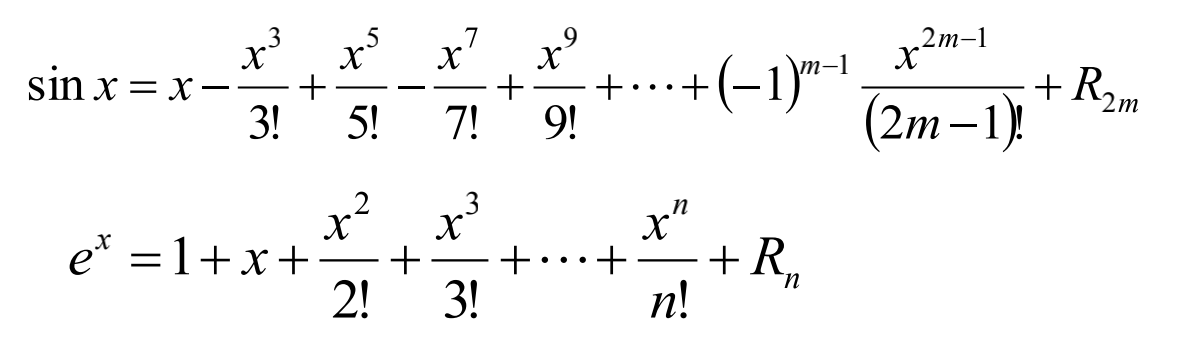
在实践中,往往需要做一定程度的变换。
给定正实数x,计算$e^x$=?
一种可行的思路是求整数k和小数r,使得:
$x= k\times \ln 2+2, |r|\le0.5\times \ln 2$
从而:
$$ e^x= e^{ k\times \ln 2+2}$$
$$=e^{ k\times \ln 2}\cdot e^r$$
$$=2^k \cdot e^r$$
Taylor公式应用2
考察Gini系数的图像、熵、分类误差率三者之间的关系
将$f(x)=-\ln x$在x=1出一阶展开,忽略高阶无穷小,得到$f^{‘}(x)\approx1-x$
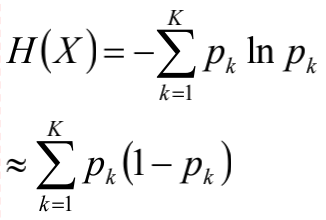
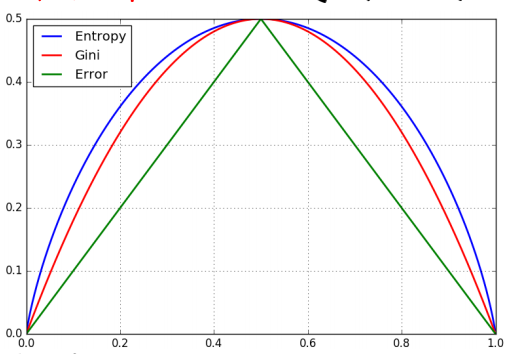
具体细节在决策树中描述。
方向导数
如果函数z=f(x,y)在点P(x,y)是可微分的,那么,函数在该点沿任意方向L的方向导数都存在,且有:
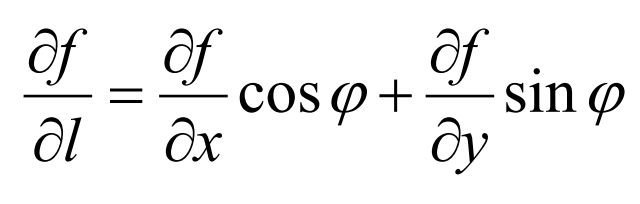
其中,$\varphi$为x轴到方向L的转角。
梯度
设函数z=f(x,y)在平面区域D内具有一阶连续偏导数,这对于每一个点P(x,y)$\in$D,向量:
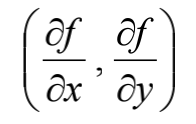
为函数z=f(x,y)在点P的梯度,记作$gradf(x,y)$。
- 梯度的方向是函数在该点变化最快的方向。
- 梯度下降法
概率论
- 对概率论的认识
P(x)$\in$[0,1]
p=0,事件出现的概率为0$\to$事件不会发生吗?
我们希望概率为0,但是实际上定义域为连续的。比如投针到桌子上,我们可以认为针的尖端为0,这样理论上桌面被投中的概率为0,但是,实际上还是会被投中。当然,这是极限情况,我们可以基本无视。
若x为离散/连续变量,则p(x=$x_0$)表示$x_0$发生的概率/概率密度。
累计分布函数
$\Phi$一定为单增函数
min($\Phi(x)$)=0,max($\Phi(x)$)=0。
将值域为[0,1]的某单增函数y=F(x)看成:X事件的累积概率函数(CDF)
若F(x)可导,则f(x)=F'(x)为某概率密度函数(PDF)。
古典概型
举例:将n个不同的球放入N(N$\ge$n)个盒子中,假设盒子容量无限,求事件A{每个盒子至多有一个球}的概率。
解:
基本事件总数:
- 第一个球,N种放法
- 第二个球,N种放法
- ……
- 共有:$N^n$种放法
每个盒子至多放1个球的事件数:
- 第一个球,N种放法
- 第二个球,N-1种放法
- ……
- 共有:N(N-1)(N-2)…(N-n+1)
$P(A)=\frac{P_N^n}{N^n}$
生日悖论
假定班内50人,假设一年365天,则至少有2人生日相同的概率是多少?

那么n=50,N=365。只需1-(每个人生日都不同)最终结果97%。
这和我们的经验出现偏差,告诉我们,我们的先验不一定正确。
装箱问题
将12件正品和3件次品随机装在3个箱子中,每箱子装5件,则每箱中恰有一件次品的概率是多少?
解:

组合数
装箱问题与组合数的关系

组合数的背后
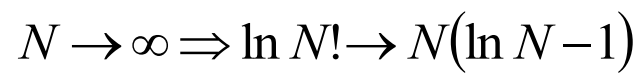
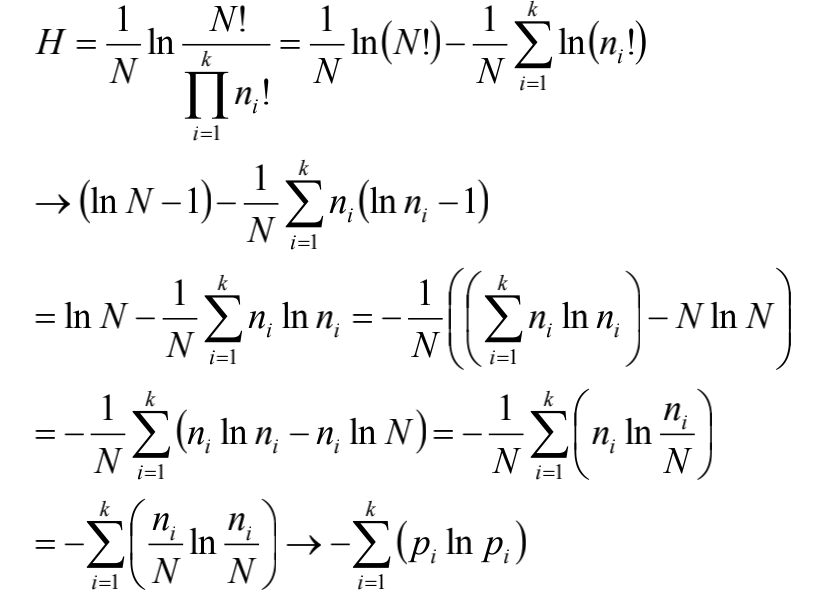
最终结果就是信息论中的信息熵。
概率公式
条件概率:
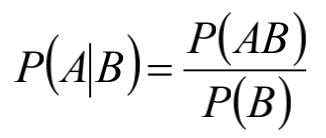
全概率公式:
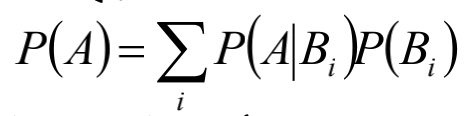
贝叶斯(Bayes)公式:
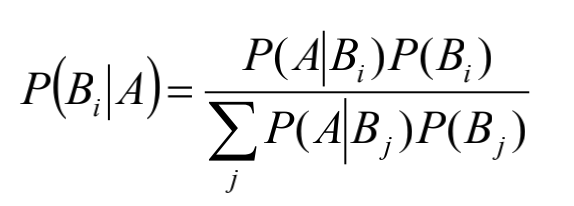
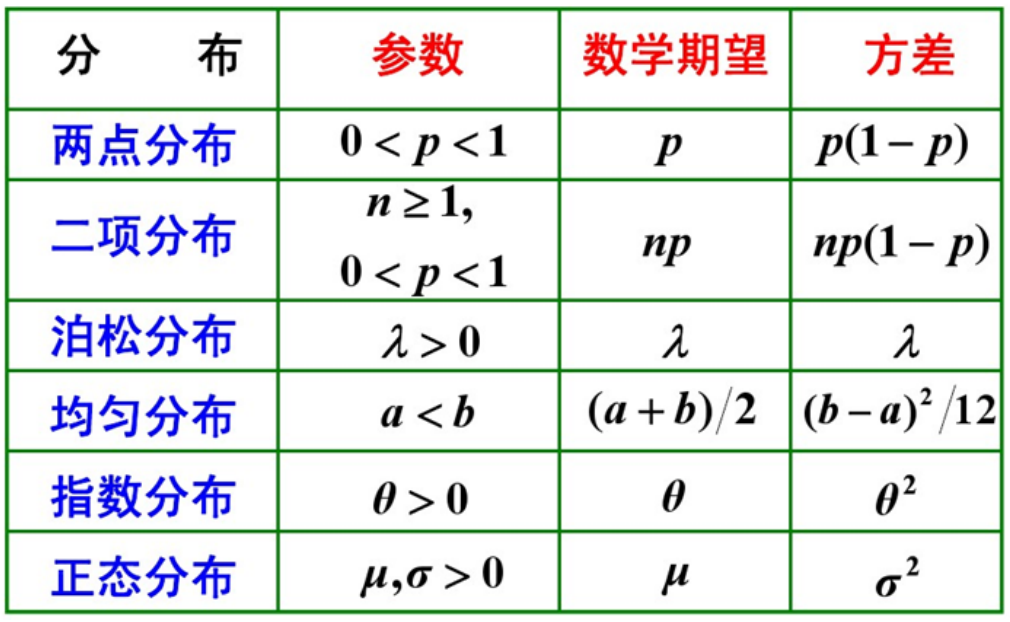
需要掌握各种分布
二项分布Bernoulli distribution
- 期望np,方差np(1-p)
- 离散的
泊松分布Poisson distribution
- 可以通过泰勒展开式获得泊松分布
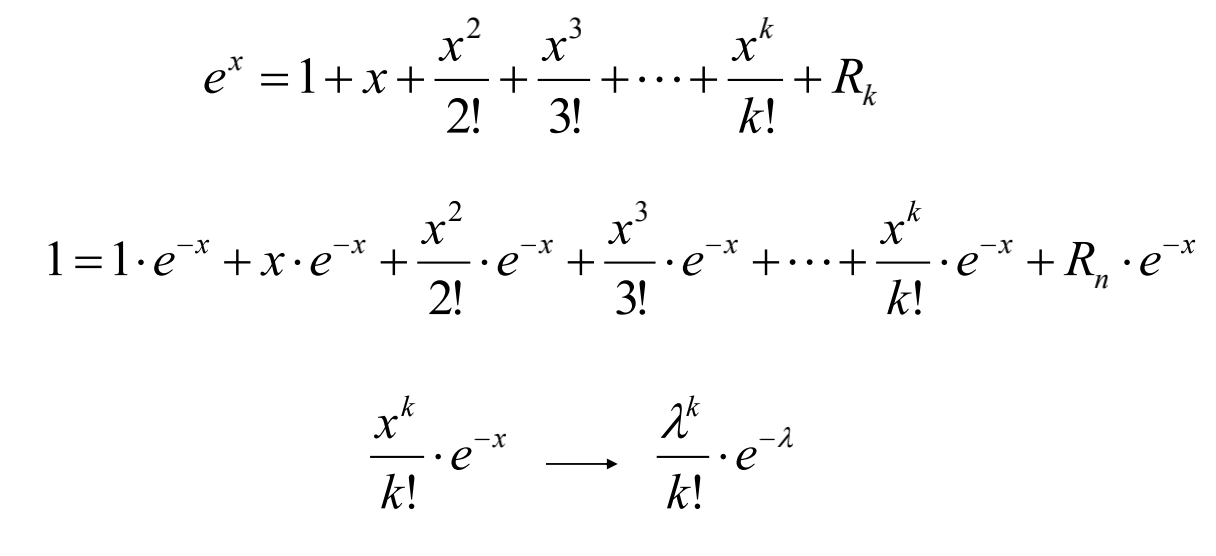
期望方差均为$\lambda$
离散的
均匀分布
期望0.5(a+b),方差$(b-a)^2/12$
连续的
指数分布
- 无记忆性
正态分布(高斯分布)
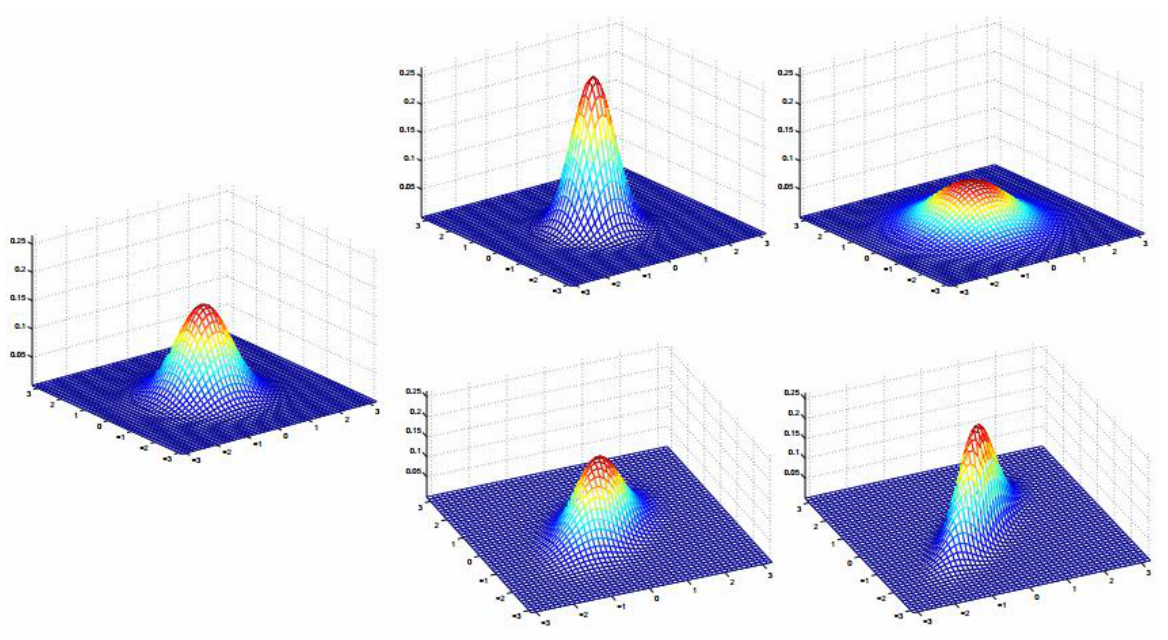
指数族
某一函数可以写作类似如下指数形式:
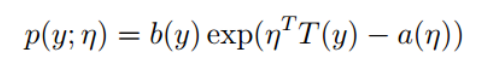
这个函数描述的分别可以称为指数族分布。例如Bernoulli分布、高斯分别、泊松分布,伯努利分布、Gamma分布等。
Bernoulli分布:
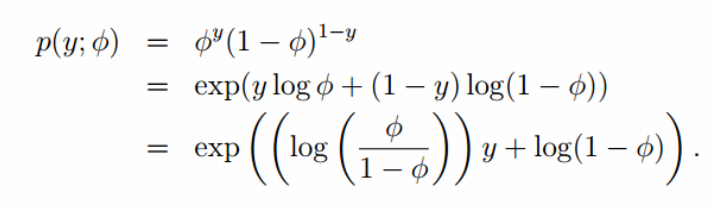
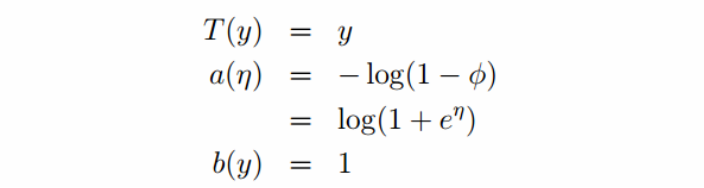
在推导过程中出现了logistic方程:
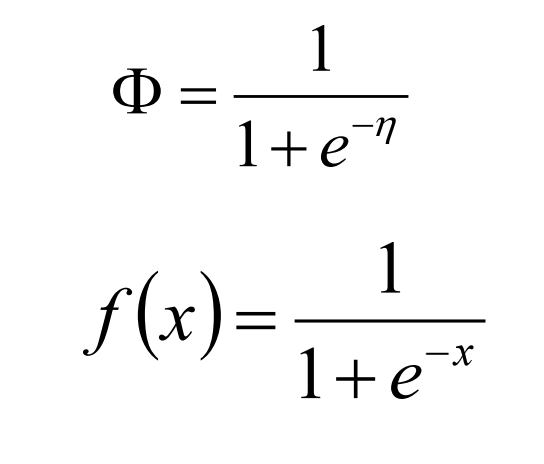
这也就是sigmoid函数,图像如下:
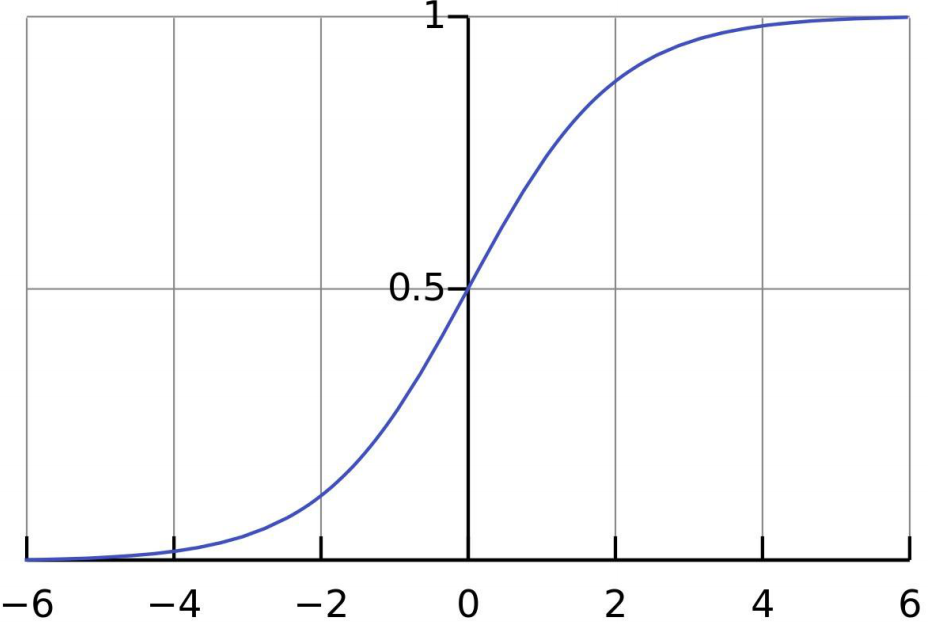
sigmoid函数的导数:
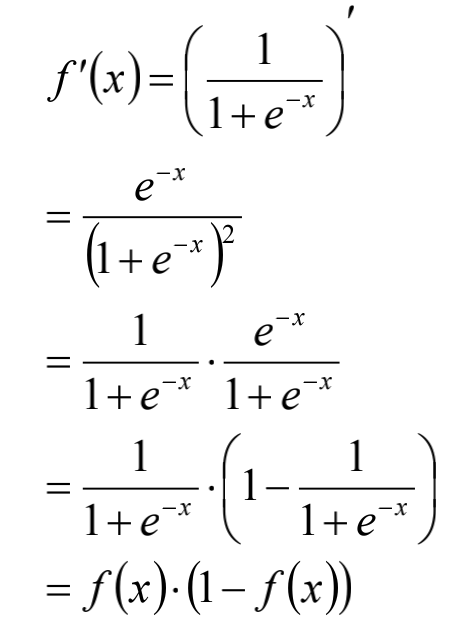




















 1718
1718











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








