求一个大数的所有因数（复杂度O(sqrt(n)) ）

最新推荐文章于 2021-03-21 14:28:08 发布

九羽-

最新推荐文章于 2021-03-21 14:28:08 发布

阅读量4.3k

点赞数 9

分类专栏：小知识点

本文链接：https://blog.csdn.net/weixin_43828245/article/details/100089113

版权

小知识点专栏收录该内容

47 篇文章

订阅专栏

求一个数的所有因数

1.寻找配对，在平方根停下

i遍历1-sqrt(n)，若i为约数，则n / i也为约数。

如果你观察一个数字的各个因数，你可以发现因数总是成对存在。换句话说，你可以通过一个数的两个特定的因数的乘积得出这个数。如果你已经知道了一个因数，你可以用这个数/因数来得出它的另一个因数。

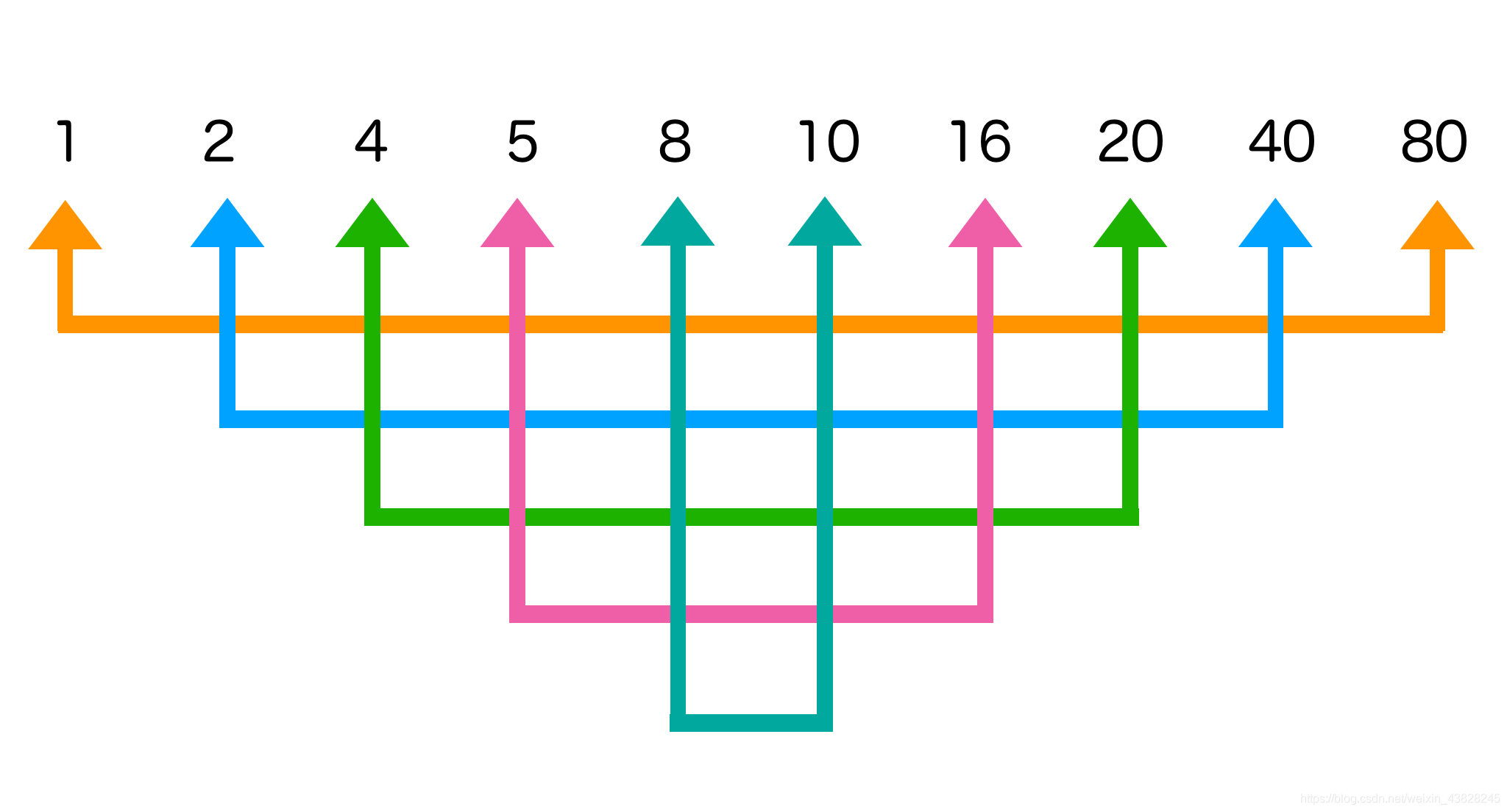
再看图，一个数n有若干因数，那么一定是两个因数的乘积能够得到n。这里n = 80，那么求的因数一定是两辆配对的，分割线就是sqrt(80) = 8 . 在8以内找到了因数1,2,4,5,8 。那么这些因数一定是乘以另外一个整数才能等于80，这里乘的另外一个数就是另外一个因数。所有最后80的因数有{1,2,4,5,8,10,16,20,40,80}。

代码：因为在中间的时候可能会有重复，比如9的因数会出现3*3=9，所有用set存比较方便。

#include <bits/stdc++.h>

using namespace std;

set <int> S;
int n;

int main()
{
    cin >> n;
    for ( int i=1; i<=sqrt(n); i++ ) {
        if ( n%i==0 ) {
            S.insert(i);
            S.insert(n/i);
        }
    }
    for ( set<int>::iterator it=S.begin(); it!=S.end(); it++ ) {
        cout << *it << " ";
    }

    return 0;
}

例题：http://codeforces.com/gym/102302/problem/B