LGESQL: Line Graph Enhanced Text-to-SQL Model with Mixed Local and Non-Local Relations 论文笔记

最新推荐文章于 2024-09-16 07:35:31 发布

weixin_43829169

最新推荐文章于 2024-09-16 07:35:31 发布

阅读量1.3k

点赞数 1

文章标签： nlp

本文链接：https://blog.csdn.net/weixin_43829169/article/details/121678305

版权

文章目录

摘要
1.Introduction
2.Preliminaries
3.Method
4.总结

摘要

这项工作旨在解决 Text-to-SQL 任务中具有挑战性的异质图（由不同成分组成的图）编码问题。以前的方法通常是以节点为中心，仅仅利用不同的权重矩阵来对边类型进行参数化，这些方法

忽略了嵌入在边的拓扑结构中的丰富语义信息
不能区分每个节点的局部和非局部关系

为此，我们提出了一个 Line Graph Enhanced Text-SQL（LGESQL） 模型来挖掘底层的关系特征，而无需构建元路径。由于line graph的存在，信息不仅通过节点之间的连接，而且通过有向边的拓扑结构更有效地传播。此外，在图的迭代过程中，局部和非局部的关系都被不同程度地整合。我们还设计了一个辅助任务，叫做图的修剪，以提高encoder的辨别能力。在撰写本报告时，我们的框架在跨领域文本到SQL基准的Spider上取得了 state-of-the-art（GLOVE为62.8%，ELECTRA为72.0%）。

1.Introduction

Text-to-SQL任务旨在给出相应的数据库模式，将自然语言问题转换为SQL查询。它已经在学术界和工业界被广泛研究，以建立数据库的自然语言接口。
一个艰巨的问题是如何联合编码问题词和数据库模式项目（包括表和列），以及这些异质输入之间的各种关系。通常情况下，以前的文献利用以节点为中心的图形神经网络（GNN）来汇总相邻节点的信息，GNNSQL采用了关系图卷积网络（RGCN）来考虑模式项之间的不同边类型
然而，这些边特征是直接从一个固定大小的参数矩阵中获取的，可能会有一个缺点：不知道文本化的信息，特别是边的结构拓扑。元路径被定义为连接两个对象的组合关系，它可以用来捕捉多跳语义，举例：在图1(a)中，Q-exact match-C 和 C-belong to-T 可以形成一个2跳元路径，表示某个表T 有一个列C正好在问题Q中被提到
尽管RATSQL引入了一些有用的元路径，如 C-same table-C，但它处理所有的关系，无论是1跳还是多跳，都是以同样的方式（相对位置嵌入）表示在一个完整的图中。
如果不区分局部（1跳邻居）和非局部邻居，见图1(b)，每个节点将平等地关注所有其他节点，这可能导致过度平滑问题 (局部和非局部邻居应该被区别对待)
此外，元路径目前是由领域专家构筑的，或者通过广度优先搜索来探索。不幸的是，可能的元路径的数量随着路径长度的增加而呈指数级增长，在其中选择最重要的子集是一个NP-complete问题
为了解决上述限制，我们提出了一个 Line Graph Enhanced Text-SQL（LGESQL） 模型，它明确考虑了边的拓扑结构。
根据 line graph（线型图）的定义，我们首先从原来的以节点为中心的图中构建一个以边为中心的图，这两个图显示了节点和边的结构拓扑。
迭代地，两个图中的每个节点都从其邻域收集信息，并从双图中提取边缘特征来更新其表示。对于以节点为中心的图，我们将局部和非局部的边特征都纳入计算。
局部边特征表示 1跳关系，由 line graph 中的 node embeddings 动态提供，而非局部边特征则直接从参数矩阵中提取，这种区别鼓励模型要更多地关注局部的边特征。

2.Preliminaries

2.1 Problem definition

整个输入节点为中心的异质图 $G^{n}$ = ( $V^{n}$ , $R^{n}$ ) 由三种类型的节点组成，即
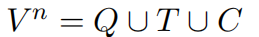
在这里插入图片描述

其中，Q为问题，T为对应的数据库 schema 的Table，C 为 column，R 是边的类型
$V^{n}|$ 是节点总数

2.2 Meta-path

如图1(a) 所示，一个 meta-path 代表一个路径
它在两个类型 $\tau_{1}$ 和 $\tau_{2}$ 的节点之间描述了一组复合关系 r = $r_{1}$ $\circ$ $r_{2}$ $\cdot$ $\cdot$ $\cdot$ $\circ$ $r_{l}$ (即描述了两个节点之间存在的边的类型信息，边的类型包括 QUESTION，TABLE，COLUMN)
在本文的讨论中，我们使用 local 来表示长度为 1 的路径（局部路径），而长度 大于1 的路径为非局部路径。
关系邻接矩阵 $R^{n}$ 中包含局部关系和非局部关系

2.3 Line Graph

离散数学里面的对偶图，把原图的边转换为节点，把节点转化为边

在 line graph $G^{e}$ = ( $V^{e}$ , $R^{e}$ ) 中的每一个节点 $v_{i}^{e}$ , $i$ = 1,2,…,| $V^{e}$ | 可以唯一映射到原始节点中心图 $G^{n}$ = ( $V^{n}$ , $R^{n}$ )的一条有向边 $r^{n}_{st}$ ，或者 $v_{s}^{n}$ --> $v_{t}^{n}$
Function f 将源节点和目标节点的索引元组（s,t）映射到 line graph $G^{e}$ 中点的索引（相当于把 $G^{n}$ 中两个节点之间的边映射到 $G^{e}$ 中的节点），表示为 i = f(s,t)，反向映射表示为 $f^{-1}$ （相当于把

最低0.47元/天解锁文章